Základ (lineární algebra) - Basis (linear algebra)

Stejný vektor může být zastoupen na dvou různých základnách (fialové a červené šipky).

V matematiky , je množina B vektorů ve vektorovém prostoru V, se nazývá základ , pokud každý prvek V může být napsána jedinečným způsobem jako konečný lineární kombinace prvků B . Koeficienty této lineární kombinace jsou označovány jako komponenty nebo souřadnic vektoru s ohledem na B . Prvky základu se nazývají základní vektory .

Ekvivalentně, sada B je základ, pokud její prvky jsou lineárně nezávislé a každý prvek V je lineární kombinací prvků B . Jinými slovy, základem je lineárně nezávislá množina překlenutí .

Vektorový prostor může mít několik základen; nicméně všechny báze mají stejný počet prvků, nazývaný dimenze vektorového prostoru.

Tento článek se zabývá hlavně vektorovými prostory s konečnou dimenzí. Mnoho principů však platí také pro nekonečně dimenzionální vektorové prostory.

Definice

Základ B na vektorovém prostoru V přes pole F (jako jsou reálná čísla R nebo komplexní čísla C ) je lineárně nezávislé podmnožina z V, která se rozkládá v V . To znamená, že podskupina B z V, je základem, pokud splňuje dvou následujících podmínek:

• vlastnost lineární nezávislosti :

  Pro každou konečnou podmnožinu z B , je-li pro některé v F , pak ; a${\ Displaystyle \ {\ mathbf {v} _ {1}, \ dotsc, \ mathbf {v} _ {m} \}}$${\ Displaystyle c_ {1} \ mathbf {v} _ {1} +\ cdots +c_ {m} \ mathbf {v} _ {m} = \ mathbf {0}}$${\ displaystyle c_ {1}, \ dotsc, c_ {m}}$${\ Displaystyle c_ {1} = \ cdots = c_ {m} = 0}$

• klenout vlastnost:

  pro každý vektor v ve V lze vybrat ve F a v B tak, že .${\ displaystyle a_ {1}, \ dotsc, a_ {n}}$${\ Displaystyle \ mathbf {v} _ {1}, \ dotsc, \ mathbf {v} _ {n}}$${\ Displaystyle \ mathbf {v} = a_ {1} \ mathbf {v} _ {1} +\ cdots +a_ {n} \ mathbf {v} _ {n}}$

Tyto skaláry se nazývají souřadnice vektoru V s ohledem na základ B , a od první vlastnosti, které jsou jednoznačně určeny. ${\ displaystyle a_ {i}}$

Vektorový prostor, který má konečný základ, se nazývá konečný-dimenzionální . V tomto případě lze konečnou podmnožinu považovat za B samotnou ke kontrole lineární nezávislosti ve výše uvedené definici.

Často je vhodné nebo dokonce nutné mít uspořádání na základě vektorů, například při diskusi o orientaci , nebo když vezmeme v úvahu skalární koeficienty vektoru s ohledem na základ, aniž bychom výslovně odkazovali na elementy základny. V tomto případě je uspořádání nutné pro přiřazení každého koeficientu k odpovídajícímu základnímu prvku. Toto uspořádání lze provést očíslováním základních prvků. Abychom zdůraznili, že byl vybrán řád, hovoří se o uspořádaném základě , který tedy není pouze nestrukturovanou sadou , ale sekvencí , indexovanou rodinou nebo podobným; viz § Objednané základny a souřadnice níže.

Příklady

Tento obrázek ilustruje standardní základ v R ² . Modré a oranžové vektory jsou prvky základu; zelený vektor lze vyjádřit pomocí základních vektorů, a proto je na nich lineárně závislý .

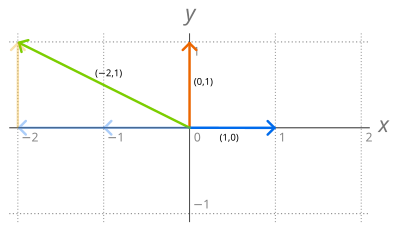
• Sada R ² z uspořádaných dvojic z reálných čísel je vektorový prostor pro následující vlastnosti:

  komponentní přidání

  ${\ Displaystyle (a, b)+(c, d) = (a+c, b+d),}$

  a skalární násobení

  ${\ Displaystyle \ lambda (a, b) = (\ lambda a, \ lambda b),}$

  kde je nějaké skutečné číslo. Jednoduchý Základem tohoto vektorového prostoru, nazývané standardní základ se skládá ze dvou vektorů e ₁ = (1,0) a e ₂ = (0,1) , protože, jakýkoliv vektor, V = ( , b ) z R ² mohou být být jedinečně zapsán jako ${\ Displaystyle \ lambda}$

  ${\ Displaystyle \ mathbf {v} = a \ mathbf {e} _ {1}+b \ mathbf {e} _ {2}.}$

  Jakékoliv jiné dvojice lineárně nezávislých vektorů R ² , jako je (1, 1) a (-1, 2) , formy také základ R ² .

• Obecněji, v případě, F je pole , soubor z n -tuples prvků F je vektorový prostor pro podobně definované sčítání a skalární násobení. Nechat ${\ displaystyle F^{n}}$

  ${\ Displaystyle \ mathbf {e} _ {i} = (0, \ ldots, 0,1,0, \ ldots, 0)}$

  je n -tuple se všechny složky se rovnají 0, s výjimkou i th, která je 1. Pak je báze , která se nazývá

  standardně z${\ Displaystyle \ mathbf {e} _ {1}, \ ldots, \ mathbf {e} _ {n}}$${\ displaystyle F^{n},}$${\ displaystyle F^{n}.}$
• Jestliže F je pole, tím polynom kroužek F [ X ] o polynomů v jednom Neurčitý je F -vector prostor, a má plošnou B , nazvaný monomial základ , skládající se ze všech monomials :

  ${\ Displaystyle B = \ {1, X, X^{2}, \ ldots \}.}$

  Základem je také jakákoli sada polynomů, která obsahuje přesně jeden polynom každého stupně. Taková sada polynomů se nazývá polynomiální sekvence . Příklady (mezi mnoha) takových polynomických sekvencí jsou Bernsteinovy ​​polynomy a Chebyshevovy polynomy .

Vlastnosti

Mnoho vlastností konečných bází vyplývá z výměnné lemma Steinitz , který uvádí, že pro jakýkoli vektorovém prostoru V , dané konečné trvající sady S a lineárně nezávislé nastavení L a n prvků V , může se nahradit n dobře zvolené prvky S o prvky L získat spanning sadu obsahující L , která má své dalších prvků v s , a které mají stejný počet prvků, jako je s .

Většina vlastností vyplývajících z Steinitzova výměnného lemmatu zůstává pravdivá, když neexistuje žádná konečná množina rozpětí, ale jejich důkazy v nekonečném případě obecně vyžadují zvolený axiom nebo jeho slabší formu, jako je ultrafiltrové lemma .

Pokud V je vektorový prostor nad polem F , pak:

• Jestliže L je lineárně nezávislá podmnožina rozpětí množiny S ⊆ V , pak existuje základ B takový, že

  ${\ Displaystyle L \ subseteq B \ subseteq S.}$

• V má základ (toto je předchozí vlastnost, kde L je prázdná množina a S = V ).
• Všechny základy V mají stejnou mohutnost , která se nazývá dimenze ve V. . Toto je věta o dimenzi .
• Sada generující S je základem V případě, a pouze v případě, že je minimální, to znamená, že žádná vlastní podmnožina z S je také generující sadu V .
• Lineárně nezávislá množina L je základem tehdy a jen tehdy, je -li maximální, to znamená, že není vlastní podmnožinou žádné lineárně nezávislé sady.

Pokud V je vektorový prostor dimenze n , pak:

• Podskupina V s n prvky je základem právě tehdy, je -li lineárně nezávislá.
• Podskupina V s n prvků je základem tehdy a jen tehdy, je-li klenout sada V .

Souřadnice

Nechť V je vektorový prostor konečné dimenze n nad polem F a

${\ Displaystyle B = \ {\ mathbf {b} _ {1}, \ ldots, \ mathbf {b} _ {n} \}}$

být základem V . Podle definice základu může být každé v ve V zapsáno jedinečným způsobem jako

${\ Displaystyle \ mathbf {v} = \ lambda _ {1} \ mathbf {b} _ {1} +\ cdots +\ lambda _ {n} \ mathbf {b} _ {n},}$

kde koeficienty jsou skalární (to znamená, že prvky F ), které se nazývají souřadnice z V průběhu B . Pokud však hovoříme o sadě koeficientů, ztratíme korespondenci mezi koeficienty a základními prvky a několik vektorů může mít stejnou sadu koeficientů. Například, a mají stejnou sadu koeficientů {2, 3} a jsou různé. Často je proto vhodné pracovat s uspořádaným základem ; to se obvykle provádí indexováním základních prvků podle prvních přirozených čísel. Potom souřadnice vektoru tvoří sekvenci podobně indexovanou a vektor je zcela charakterizován sekvencí souřadnic. Řazený základ se také nazývá rámec , slovo běžně používané v různých kontextech pro odkazování na sekvenci dat umožňující definovat souřadnice. ${\ Displaystyle \ lambda _ {1}, \ ldots, \ lambda _ {n}}$${\ Displaystyle 3 \ mathbf {b} _ {1} +2 \ mathbf {b} _ {2}}$${\ Displaystyle 2 \ mathbf {b} _ {1} +3 \ mathbf {b} _ {2}}$

Nechť, jako obvykle, je množina z n -tuples prvků ze F . Tato sada je F -vektorový prostor s přidáním a skalárním násobením definovaným po komponentách. Mapa ${\ displaystyle F^{n}}$

${\ Displaystyle \ varphi: (\ \ lambda _ {1}, \ ldots, \ lambda _ {n}) \ mapsto \ lambda _ {1} \ mathbf {b} _ {1} +\ cdots +\ lambda _ {n } \ mathbf {b} _ {n}}$

je lineární izomorfismus z vektorového prostoru na V . Jinými slovy, je koordinovat prostor z V a n -tuple je koordinovat vektor z V . ${\ displaystyle F^{n}}$${\ displaystyle F^{n}}$${\ Displaystyle \ varphi ^{-1} (\ mathbf {v})}$

Inverzní obraz o o je n -tuple všechny, jejichž součásti jsou 0, kromě toho, že i té, která je 1. vzniku uspořádaného základ , který se nazývá jeho standardní základ nebo kanonický základ . Uspořádaný základ B je obrazem kanonického základu .${\ Displaystyle \ varphi}$${\ displaystyle \ mathbf {b} _ {i}}$${\ displaystyle \ mathbf {e} _ {i}}$${\ displaystyle \ mathbf {e} _ {i}}$${\ displaystyle F^{n}}$${\ Displaystyle \ varphi}$${\ displaystyle F^{n}}$

Z toho, co předchází, že každý objednaný Základem je obraz pomocí lineárního izomorfismu kanonického základě , a že každý lineární izomorfismus od do V, může být definována jako izomorfismus, která mapuje kanonický základ na danou objednanou bázi V . Jinými slovy, je ekvivalentní k definování uspořádané základ V , nebo lineární izomorfismus z na V . ${\ displaystyle F^{n}}$${\ displaystyle F^{n}}$${\ displaystyle F^{n}}$${\ displaystyle F^{n}}$

Změna základu

Nechť V být vektorový prostor dimenze n přes pole F . Vzhledem k tomu, dva (objednávku) základny a z V , je často užitečné vyjádřit souřadnic vektoru x s ohledem na pokud jde o souřadnic s ohledem na to může být provedeno pomocí změny-of-základě vzorce , který je popsán níže . Dolní indexy „starý“ a „nový“ byly vybrány, protože je obvyklé odkazovat na a jako na starý základ a nový základ . Je užitečné popsat staré souřadnice pomocí nových, protože obecně má člověk výrazy zahrnující staré souřadnice a pokud chce získat ekvivalentní výrazy, pokud jde o nové souřadnice; toho se dosáhne nahrazením starých souřadnic jejich výrazy ve smyslu nových souřadnic. ${\ displaystyle B _ {\ text {old}} = (\ mathbf {v} _ {1}, \ ldots, \ mathbf {v} _ {n})}$${\ displaystyle B _ {\ text {new}} = (\ mathbf {w} _ {1}, \ ldots, \ mathbf {w} _ {n})}$${\ displaystyle B _ {\ mathrm {old}}}$${\ displaystyle B _ {\ mathrm {new}}.}$${\ displaystyle B _ {\ mathrm {old}}}$${\ displaystyle B _ {\ mathrm {new}}}$

Nové základní vektory jsou obvykle dány jejich souřadnicemi na starém základě, tj.

${\ Displaystyle \ mathbf {w} _ {j} = \ sum _ {i = 1}^{n} a_ {i, j} \ mathbf {v} _ {i}.}$

Pokud a jsou souřadnice vektoru x nad starým a novým základem, vzorec pro změnu základu je ${\ displaystyle (x_ {1}, \ ldots, x_ {n})}$${\ displaystyle (y_ {1}, \ ldots, y_ {n})}$

${\ Displaystyle x_ {i} = \ sum _ {j = 1}^{n} a_ {i, j} y_ {j},}$

pro i = 1,…, n .

Tento vzorec může být stručně napsán v maticovém zápisu. Nechť A je matice , a ${\ displaystyle a_ {i, j}}$

${\ Displaystyle X = {\ begin {bmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {bmatrix}} \ quad {\ text {and}} \ quad Y = {\ begin {bmatrix} y_ {1} \\\ vdots \\ y_ {n} \ end {bmatrix}}}$

být sloupcové vektory souřadnic V, ve staré a nové báze v tomto pořadí, pak je vzorec pro změnu souřadnic je

${\ displaystyle X = AY.}$

Vzorec lze dokázat zvážením rozkladu vektoru x na dvou základnách: jedna má

${\ Displaystyle \ mathbf {x} = \ sum _ {i = 1}^{n} x_ {i} \ mathbf {v} _ {i},}$

a

${\ Displaystyle {\ begin {aligned} \ mathbf {x} & = \ sum _ {j = 1}^{n} y_ {j} \ mathbf {w} _ {j} \\ & = \ sum _ {j = 1}^{n} y_ {j} \ sum _ {i = 1}^{n} a_ {i, j} \ mathbf {v} _ {i} \\ & = \ sum _ {i = 1} ^{n} \ left (\ sum _ {j = 1}^{n} a_ {i, j} y_ {j} \ right) \ mathbf {v} _ {i}. \ end {aligned}}}$

Vzorec pro změnu základu pak vyplývá z jedinečnosti rozkladu vektoru na základě zde ; to je ${\ displaystyle B _ {\ text {old}}}$

${\ Displaystyle x_ {i} = \ sum _ {j = 1}^{n} a_ {i, j} y_ {j},}$

pro i = 1,…, n .

Související pojmy

Modul zdarma

Pokud někdo nahradí pole vyskytující se v definici vektorového prostoru prstenem , získá definici modulu . U modulů je lineární nezávislost a rozpětí množin definováno přesně jako u vektorových prostorů, ačkoli „ generující množina “ se používá častěji než u „překlenovací sady“.

Stejně jako pro vektorové prostory je základem modulu lineárně nezávislá podmnožina, která je také generující sadou. Zásadní rozdíl oproti teorii vektorových prostorů spočívá v tom, že ne každý modul má základ. Modul, který má základ, se nazývá bezplatný modul . Volné moduly hrají zásadní roli v teorii modulů, protože je lze použít k popisu struktury nesvobodných modulů prostřednictvím volných rozlišení .

Modul přes celá čísla je přesně to samé jako abelianská skupina . Volný modul přes celá čísla je tedy také volnou abelianskou skupinou. Volné abelianské skupiny mají specifické vlastnosti, které nejsou sdíleny moduly přes jiné prstence. Konkrétně, každá podskupina volné abelian skupiny je volný abelian skupina, a, pokud G je podskupina konečně vytvořeného volného abelian skupiny H (tj abelian skupina, která má konečnou základ), je základem z H a celé číslo 0 ≤ k ≤ n takové, že je základem G , u některých nenulových celých čísel . Podrobnosti viz Volná abelianská skupina § Podskupiny . ${\ Displaystyle \ mathbf {e} _ {1}, \ ldots, \ mathbf {e} _ {n}}$${\ Displaystyle a_ {1} \ mathbf {e} _ {1}, \ ldots, a_ {k} \ mathbf {e} _ {k}}$${\ displaystyle a_ {1}, \ ldots, a_ {k}}$

Analýza

V kontextu nekonečně dimenzionálních vektorových prostorů nad skutečnými nebo komplexními čísly termín Hamelský základ (pojmenovaný poGeorgu Hamelovi) neboalgebraický základlze použít k označení základu definovaného v tomto článku. To je třeba odlišit od ostatních pojmů „základu“, které existují, když jsou nekonečně dimenzionální vektorové prostory vybaveny zvláštní strukturou. Nejdůležitějšími alternativami jsouortogonální bázenaHilbertově prostoru,Schauderovy bázeaMarkushevichovy bázenanormovaných lineárních prostorech. V případě reálných číselRviděných jako vektorový prostor nad polemQracionálních čísel jsou Hamelské báze nepočítatelné a mají konkrétněmohutnostkontinua, což jekardinální číslo ,kdeje nejmenší nekonečný kardinál, kardinál celých čísel. ${\ Displaystyle 2^{\ aleph _ {0}}}$${\ displaystyle \ aleph _ {0}}$

Společným rysem ostatních pojmů je, že umožňují vytváření nekonečných lineárních kombinací základních vektorů za účelem generování prostoru. To samozřejmě vyžaduje, aby v těchto prostorech bylo smysluplně definováno nekonečné množství, jako je tomu v případě topologických vektorových prostorů - velké třídy vektorových prostorů zahrnujících např. Hilbertovy , Banachovy nebo Fréchetovy prostory .

Upřednostňování jiných typů základen pro nekonečně dimenzionální prostory je odůvodněno skutečností, že Hamelův základ se v Banachových prostorech stává „příliš velkým“: Pokud X je nekonečně dimenzionální normovaný vektorový prostor, který je úplný (tj. X je Banachův prostor ), pak jakýkoli hamelský základ X je nutně nepočitatelný . To je důsledek věty o kategorii Baire . Úplnost a také nekonečná dimenze jsou zásadními předpoklady v předchozím nároku. Prostory konečných dimenzí mají podle definice konečné základy a existují nekonečno-dimenzionální ( neúplné ) normované prostory, které mají spočitatelné základny Hamel. Vezměme si , prostor ze sekvencí reálných čísel, které mají pouze konečně mnoho nenulové prvky s normou . Jeho standardní základ , skládající se ze sekvencí majících pouze jeden nenulový prvek, který se rovná 1, je spočitatelný Hamelský základ. ${\ displaystyle c_ {00}}$ ${\ displaystyle x = (x_ {n})}$${\ textstyle \ | x \ | = \ sup _ {n} | x_ {n} |}$

Příklad

Při studiu Fourierových řad se člověk dozví, že funkce {1} ∪ {sin ( nx ), cos ( nx ): n = 1, 2, 3, ...} jsou „ortogonálním základem“ (skutečného nebo komplexního) vektorový prostor všech (reálných nebo komplexních) funkcí na intervalu [0, 2π], které jsou v tomto intervalu integrovatelné do čtverců, tj. funkce f splňující

${\ Displaystyle \ int _ {0}^{2 \ pi} \ left | f (x) \ right |^{2} \, dx <\ infty.}$

Funkce {1} ∪ {sin ( nx ), cos ( nx ): n = 1, 2, 3, ...} jsou lineárně nezávislé a každá funkce f, která je na [0, 2π] integrovatelná do čtverců, je "nekonečná" jejich lineární kombinace, ve smyslu, že

${\ Displaystyle \ lim _ {n \ to \ infty} \ int _ {0}^{2 \ pi} \ left | a_ {0}+\ sum _ {k = 1}^{n} \ left (a_ { k} \ cos \ left (kx \ right)+b_ {k} \ sin \ left (kx \ right) \ right) -f (x) \ right |^{2} dx = 0}$

pro vhodné (skutečné nebo komplexní) koeficienty a _k , b _k . Mnoho funkcí integrovatelných do čtverce však nelze reprezentovat jako konečné lineární kombinace těchto základních funkcí, které proto neobsahují hamelský základ. Každý hamelský základ tohoto prostoru je mnohem větší než tento pouze spočítatelný nekonečný soubor funkcí. Hamelské základy prostorů tohoto druhu obvykle nejsou užitečné, zatímco ortonormální základy těchto prostorů jsou ve Fourierově analýze zásadní .

Geometrie

Geometrické pojmy afinního prostoru , projektivního prostoru , konvexní množiny a kužele mají související pojmy základ . Afinní základ pro n rozměrné afinního prostoru je bodů lineárního poloze . A${\ displaystyle n+1}$projektivním základem jsoubody v obecné poloze, v projektivním prostoru dimenzen. A${\ displaystyle n+2}$konvexní základna zmnohostěnuje množina vrcholů jehokonvexní trupu. Akuželový základ tvoří jeden bod za hranou polygonálního kužele. Viz takéHilbertův základ (lineární programování).

Náhodný základ

Pro rozdělení pravděpodobnosti v R ⁿ s funkcí hustoty pravděpodobnosti , jako je ekvidistribuce v n -dimenzionální kouli s ohledem na Lebesgueovu míru, lze ukázat, že n náhodně a nezávisle vybraných vektorů bude tvořit základ s pravděpodobností jedna , která je vzhledem k tomu, že n lineárně závislých vektorů x ₁ ,…, x _n v R ⁿ by mělo splňovat rovnici det [ x ₁ ⋯ x _n ] = 0 (nulový determinant matice se sloupci x _i ) a množinu nul netriviálního polynomu má nulovou míru. Toto pozorování vedlo k technikám aproximace náhodných základen.

Empirická distribuce délek N párových téměř ortogonálních řetězců vektorů, které jsou nezávisle náhodně vzorkovány z n -dimenzionální krychle [−1, 1] ⁿ jako funkce dimenze, n . Boxplots ukazují druhý a třetí kvartil těchto dat pro každé n , červené pruhy odpovídají mediánům a modré hvězdy označují prostředky. Červená křivka ukazuje teoretickou mez danou ekv. (1) a zelená křivka ukazuje upřesněný odhad.

Je obtížné numericky zkontrolovat lineární závislost nebo přesnou ortogonalitu. Proto se používá pojem e-ortogonality. Pro prostory s vnitřním součinem je x ε-ortogonální k y, pokud (tj. Kosinus úhlu mezi x a y je menší než ε ). ${\ Displaystyle \ left | \ left \ langle x, y \ right \ rangle \ right |/\ left (\ left \ | x \ right \ | left \ | y \ right \ | \ right) <\ varepsilon}$

Ve vysokých dimenzích jsou dva nezávislé náhodné vektory s vysokou pravděpodobností téměř ortogonální a počet nezávislých náhodných vektorů, které jsou všechny s danou vysokou pravděpodobností párově téměř ortogonální, exponenciálně roste s dimenzí. Přesněji zvažte ekvidistribuci v n -dimenzionální kouli. Vyberte N nezávislých náhodných vektorů z koule (jsou nezávislé a identicky rozmístěné ). Nechť θ je malé kladné číslo. Pak pro

${\ Displaystyle N \ leq e^{\ frac {\ epsilon^{2} n} {4}} [-\ ln (1- \ theta)]^{\ frac {1} {2}}}$

(Rovnice 1)

N náhodných vektorů je všech párů e-ortogonálních s pravděpodobností 1- θ . Tento N roste exponenciálně s dimenzí n a dostatečně velkým n . Tato vlastnost náhodných bází je projevem takzvaného jevu koncentrace koncentrace . ${\ Displaystyle N \ gg n}$

Obrázek (vpravo) ukazuje rozložení délek N párových téměř ortogonálních řetězců vektorů, které jsou nezávisle náhodně vzorkovány z n -dimenzionální krychle [−1, 1] ⁿ jako funkce dimenze, n . V kostce je nejprve náhodně vybrán bod. Druhý bod je náhodně vybrán ve stejné krychli. Pokud byl úhel mezi vektory v rozmezí π/2 ± 0,037π/2, pak byl vektor zachován. V dalším kroku se ve stejné hyperkrychli vygeneruje nový vektor a vyhodnotí se jeho úhly s dříve generovanými vektory. Pokud jsou tyto úhly v rozmezí π/2 ± 0,037π/2, pak je vektor zachován. Proces se opakuje, dokud se řetěz téměř ortogonality nerozbije, a zaznamená se počet takových párových téměř ortogonálních vektorů (délka řetězce). Pro každé n bylo pro každou dimenzi numericky konstruováno 20 párových téměř ortogonálních řetězců. Je prezentováno rozdělení délky těchto řetězců.

Důkaz, že každý vektorový prostor má svůj základ

Nechť V být jakýkoli vektorový prostor přes některé oblasti F . Nechť X je množina všech lineárně nezávislých podmnožin V. .

Množina X je neprázdná, protože prázdná množina je nezávislou podmnožinou V a je částečně uspořádána zahrnutím, které je jako obvykle označeno ⊆ .

Nechť Y je podmnožinou X, která je zcela uspořádána pomocí ⊆ , a nechť L _Y je sjednocením všech prvků Y (což jsou samy o sobě určité podmnožiny V ).

Protože ( Y , ⊆) je zcela uspořádané, každá konečná podmnožina L _Y je podmnožinou prvku Y , což je lineárně nezávislá podmnožina V , a tudíž L _Y je lineárně nezávislá. Tak L _Y je prvek X . Z tohoto důvodu, L _Y je horní mez pro Y v ( X , ⊆): je to prvek X , která obsahuje každý prvek Y .

Protože X je neprázdné a každá zcela uspořádaná podmnožina ( X , ⊆) má v X horní hranici , Zornovo lemma tvrdí, že X má maximální prvek. Jinými slovy, existuje nějaký prvek L _max z X splňující podmínku, že kdykoli L _max ⊆ L pro nějaký prvek L z X , pak L = L _max .

Zbývá dokázat, že L _max je základem V . Vzhledem k tomu, L _max patří k X , již víme, že L _max je lineárně nezávislé podmnožina V .

Pokud by se některý vektor w z V, který není v rozpětí L _max , pak w nebude prvek L _max obou. Nechť L _w = L _max ∪ { w }. Tato sada je prvkem X , to znamená, že je to lineárně nezávislá podmnožina V (protože w není v rozsahu L _max a L _max je nezávislá). Protože L _max ⊆ L _w a L _max ≠ L _w (protože L _w obsahuje vektor w, který není obsažen v L _max ), je to v rozporu s _{maximálností} L _max . Tak to ukazuje, že L _{se max} klene V .

Proto L _max je lineárně nezávislé a rozpětí V . Je to tedy základ V , a to dokazuje, že každý vektorový prostor má základ.

Tento důkaz se opírá o Zornovo lemma, které je ekvivalentní zvolenému axiomu . A naopak bylo dokázáno, že pokud má každý vektorový prostor základ, pak platí axiom volby. Obě tvrzení jsou tedy ekvivalentní.

Viz také

• Základ matroidu
• Změna základu  - změna souřadnic pro vektorový prostor
• Rám vektorového prostoru
• Sférický základ  - základ používaný k vyjádření sférických tenzorů

Poznámky

Reference

Obecné reference

• Blass, Andreas (1984), „Existence základen implikuje axiom volby“, Axiomatic theory of set (PDF) , Contemporary Mathematics volume 31, Providence, RI: American Mathematical Society , s. 31–33, ISBN 978-0-8218-5026-8, MR  0763890
• Brown, William A. (1991), Matice a vektorové prostory , New York: M. Dekker, ISBN 978-0-8247-8419-5
• Lang, Serge (1987), Lineární algebra , Berlín, New York: Springer-Verlag , ISBN 978-0-387-96412-6

Historické reference

• Banach, Stefan (1922), „Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)“ (PDF) , Fundamenta Mathematicae (ve francouzštině), 3 : 133– 181, doi : 10,4064/fm-3-1-133-181 , ISSN  0016-2736
• Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Úvahy o některých aspektech elementární geometrie) (v němčině)
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (ve francouzštině), Paris: Hermann
• Dorier, Jean-Luc (1995), „Obecný nástin geneze teorie vektorového prostoru“ , Historia Mathematica , 22 (3): 227–261, doi : 10,1006/hmat.1995.1024 , MR  1347828
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (ve francouzštině), Chez Firmin Didot, père et fils
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (v němčině), dotisk: Hermann Grassmann. Přeložil Lloyd C. Kannenberg. (2000), The Extension Theory , Kannenberg, LC, Providence, RI: American Mathematical Society , ISBN 978-0-8218-2031-5
• Hamel, Georg (1905), „Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f (x+y) = f (x)+f (y)“ , Mathematische Annalen (v němčině), Leipzig, 60 : 459–462
• Hamilton, William Rowan (1853), Přednášky o čtveřicích , Královská irská akademie
• Möbius, August Ferdinand (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentrický počet: nový nástroj pro analytické zpracování geometrie) (v němčině), archivováno z originálu 12. dubna 2009
• Moore, Gregory H. (1995), „Axiomatizace lineární algebry: 1875–1940“, Historia Mathematica , 22 (3): 262–303, doi : 10,1006/hmat.1995.1025
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (v italštině), Turín

externí odkazy

• Instruktážní videa z Khan Academy
  • Úvod do základů podprostorů
  • Důkaz, že jakýkoli podprostorový základ má stejný počet prvků
• „Lineární kombinace, rozpětí a základní vektory“ . Esence lineární algebry . 6. srpna 2016 - prostřednictvím YouTube .
• „Základ“ , encyklopedie matematiky , EMS Press , 2001 [1994]