Rodiny řešení souvisejících diferenciálních rovnic

Besselovy funkce jsou radiální částí režimů vibrací kruhového bubnu.
Besselovy funkce , nejprve definované matematikem Danielem Bernoullim a poté zobecněné Friedrichem Besselem , jsou kanonická řešení y ( x ) Besselovy diferenciální rovnice

pro libovolné komplexní číslo α je pořadí Besselovy funkce. Ačkoli α a - α vytvářejí stejnou diferenciální rovnici, je obvyklé definovat různé Besselovy funkce pro tyto dvě hodnoty takovým způsobem, že Besselovy funkce jsou většinou hladké funkce α .
Nejdůležitější případy jsou, když α je celé číslo nebo poloviční číslo . Besselovy funkce pro celé číslo α jsou také známé jako cylindrické funkce nebo cylindrické harmonické, protože se objevují v řešení Laplaceovy rovnice ve válcových souřadnicích . Sférické Besselovy funkce s polovičním číslem α získáme, když je Helmholtzova rovnice vyřešena v sférických souřadnicích .
Aplikace Besselových funkcí
Besselova rovnice vzniká při hledání oddělitelných řešení Laplaceovy rovnice a Helmholtzovy rovnice ve válcových nebo sférických souřadnicích . Besselovy funkce jsou proto zvláště důležité pro mnoho problémů šíření vln a statických potenciálů. Při řešení problémů ve válcových souřadnicových systémech získáme Besselovy funkce celočíselného řádu ( α = n ); ve sférických problémech se získají poloviční celočíselné řády ( α = n +
1/2). Například:
Besselovy funkce se objevují i v dalších problémech, jako je zpracování signálu (např. Viz Syntéza FM , Kaiserovo okno nebo Besselův filtr ).
Definice
Protože se jedná o lineární diferenciální rovnici druhého řádu, musí existovat dvě lineárně nezávislá řešení. V závislosti na okolnostech jsou však vhodné různé formulace těchto roztoků. Různé varianty jsou shrnuty v následující tabulce a popsány v následujících částech.
Besselovy funkce druhého druhu a sférické Besselovy funkce druhého druhu jsou někdy označovány spíše N n a n n , než Y n a y n .
Besselovy funkce prvního druhu: J α
Besselovy funkce prvního druhu, označované jako J α ( x ) , jsou řešením Besselovy diferenciální rovnice. Pro celočíselné nebo kladné α jsou Besselovy funkce prvního druhu na počátku konečné ( x = 0 ); zatímco u záporných neceločíselných α se Besselovy funkce prvního druhu rozcházejí, když se x blíží nule. Funkci je možné definovat její řadovou expanzí kolem x = 0 , což lze zjistit aplikací Frobeniusovy metody na Besselovu rovnici:

kde Γ ( z ) je funkce gama , posunuté zobecnění faktoriální funkce na neceločíselné hodnoty. Besselova funkce prvního druhu je celá funkce, pokud α je celé číslo, jinak je to funkce s více hodnotami se singularitou na nule. Grafy Besselových funkcí vypadají zhruba jako oscilující sinusové nebo kosinové funkce, které se úměrně rozpadají (viz také jejich asymptotické formy níže), přestože jejich kořeny nejsou obecně periodické, kromě asymptoticky pro velká x . (Série naznačuje, že - J 1 ( x ) je derivát J 0 ( x ) , podobně jako −s x x je derivace cos x ; obecněji lze derivaci J n ( x ) vyjádřit pomocí J n ± 1 ( x ) podle níže uvedených identit .)


Graf Besselovy funkce prvního druhu,
J α ( x ) , pro celočíselné řády
α = 0, 1, 2
Pro neceločíselná α jsou funkce J α ( x ) a J - α ( x ) lineárně nezávislé, a jsou tedy dvěma řešeními diferenciální rovnice. Na druhou stranu pro celé číslo řádu n platí následující vztah (funkce gama má jednoduché póly na každém z kladných celých čísel):

To znamená, že tato dvě řešení již nejsou lineárně nezávislá. V tomto případě je potom druhým lineárně nezávislým řešením zjištěna Besselova funkce druhého druhu, jak je popsáno níže.
Besselovy integrály
Další definice Besselovy funkce pro celočíselné hodnoty n je možná pomocí integrální reprezentace:

To byl přístup, který použil Bessel, a z této definice odvodil několik vlastností funkce. Definici lze rozšířit na neceločíselné objednávky jedním ze Schläfliho integrálů pro Re ( x )> 0 :

Vztah k hypergeometrickým řadám
Besselovy funkce lze vyjádřit pomocí generalizovaných hypergeometrických řad jako

Tento výraz souvisí s vývojem Besselových funkcí z hlediska funkce Bessel – Clifford .
Vztah k Laguerreovým polynomům
Z hlediska Laguerrových polynomů L k a libovolně zvoleného parametru t lze Besselovu funkci vyjádřit jako

Besselovy funkce druhého druhu: Y α
Besselovy funkce druhého druhu, označené Y α ( x ) , příležitostně označené místo toho N α ( x ) , jsou řešeními Besselovy diferenciální rovnice, které mají na počátku singularitu ( x = 0 ) a jsou vícehodnotové . Někdy se jim říká Weberovy funkce , jak je představil HM Weber ( 1873 ), a také Neumannovy funkce po Carlu Neumannovi .

Graf Besselovy funkce druhého druhu,
Y α ( x ) , pro celočíselné řády
α = 0, 1, 2
U neceločíselných α je Y α ( x ) vztaženo k J α ( x ) o

V případě celočíselného řádu n je funkce definována tak, že limit vezmeme jako neceločíselné α, které má tendenci k n :

Pokud n je nezáporné celé číslo, máme řadu

kde je funkce digamma je logaritmická derivát z funkce gama .

Existuje také odpovídající integrální vzorec (pro Re ( x )> 0 ):

Y α ( x ) je nutné jako druhé lineárně nezávislé řešení Besselovy rovnice, když α je celé číslo. Ale Y α ( x ) má víc než to. Lze jej považovat za „přirozeného“ partnera J α ( x ) . Viz také níže uvedená podsekce o Hankových funkcích.
Když α je celé číslo, navíc, jak tomu bylo obdobně u funkcí prvního druhu, platí následující vztah:

Obě J alfa ( x ) a Y alfa ( x ) jsou holomorfní funkce o x o komplexní rovině řezu podél záporné reálné ose. Když α je celé číslo, Besselovy funkce J jsou celé funkce na x . Pokud je x drženo pevně na nenulové hodnotě, pak jsou Besselovy funkce celé funkce α .
Besselovy funkce druhého druhu, když α je celé číslo, je příkladem druhého druhu řešení ve Fuchsově větě .
Hankelovy funkce: H.(1)
α, H.(2)
α
Další důležitou formulací dvou lineárně nezávislých řešení Besselovy rovnice jsou Hankelovy funkce prvního a druhého druhu , H(1)
α( x ) a H(2)
α( x ) , definováno jako

kde i je imaginární jednotka . Tyto lineární kombinace jsou také známé jako Besselovy funkce třetího druhu ; jsou to dvě lineárně nezávislá řešení Besselovy diferenciální rovnice. Jsou pojmenovány po Hermannu Hankelovi .
Tyto formy lineární kombinace splňují řadu jednoduše vypadajících vlastností, jako jsou asymptotické vzorce nebo integrální reprezentace. Zde „jednoduché“ znamená vzhled činitele ve tvaru e i f (x) . Doopravdy , kde , jsou reálná, Besselovy funkce prvního a druhého druhu jsou skutečné a imaginární části, v uvedeném pořadí, první funkce Hankel a reálné a záporné imaginární části druhé funkce Hankel. Výše uvedené vzorce jsou tedy analogy Eulerova vzorce , které nahrazují H

 (1)
(1)
α( x ) , H(2)
α( X ) pro a , k , , jak je výslovně uvedeno v asymptotické expanzi .





Hankelovy funkce se používají k vyjádření řešení válcových vln šířících se ven a dovnitř (nebo naopak, v závislosti na konvenci znaménka pro frekvenci ).
Pomocí předchozích vztahů je lze vyjádřit jako

Pokud je α celé číslo, musí být limit vypočítán. Následující vztahy jsou platné, ať je α celé číslo nebo ne:

Zejména pokud α = m +1/2s m nezáporné celé číslo, výše uvedené vztahy přímo znamenají, že

Ty jsou užitečné při vývoji sférických Besselových funkcí (viz níže).
Hankelovy funkce připouštějí následující integrální reprezentace pro Re ( x )> 0 :

kde integrační limity indikují integraci podél obrysu, který lze zvolit takto: od −∞ do 0 podél záporné reálné osy, od 0 do ± πi podél imaginární osy a od ± πi do +∞ ± πi podél obrysové rovnoběžky na skutečnou osu.
Upravené Besselovy funkce: I α , K α
Besselovy funkce jsou platné i pro složité argumenty x a důležitým zvláštním případem je čistě imaginární argument. V tomto případě se řešení Besselovy rovnice nazývají upravené Besselovy funkce (nebo příležitostně hyperbolické Besselovy funkce ) prvního a druhého druhu a jsou definovány jako

když α není celé číslo; když α je celé číslo, pak se použije limit. Ty jsou vybrány tak, aby měly skutečnou hodnotu pro skutečné a pozitivní argumenty x . Sériové rozšíření pro I α ( x ) je tedy podobné jako pro J α ( x ) , ale bez střídavého (-1) m faktoru.
 lze vyjádřit pomocí Hankových funkcí:
lze vyjádřit pomocí Hankových funkcí:

První a druhou Besselovu funkci můžeme vyjádřit pomocí upravených Besselových funkcí (ty platí, pokud - π <arg z ≤π/2):

I α ( x ) a K α ( x ) jsou dvě lineárně nezávislá řešení modifikované Besselovy rovnice :

Na rozdíl od běžných funkcí Besselovy, které jsou oscilujících jako funkce skutečného argumentu, I alfa a K α se exponenciálně rostoucí a rozkládající se funkce, resp. Stejně jako běžná Besselova funkce J α , funkce I α jde na nulu v x = 0 pro α > 0 a je konečná v x = 0 pro α = 0 . Analogicky, k alfa diverguje u x = 0 s jedinečnost je logaritmické typu, K 0 a ½Γ (| alfa |) (2 / x ) | α | v opačném případě.

Upravené Besselovy funkce prvního druhu, I α ( x ) , pro α = 0, 1, 2, 3
|

Upravené Besselovy funkce druhého druhu, K α ( x ) , pro α = 0, 1, 2, 3
|
Dva integrální vzorce pro upravené Besselovy funkce jsou (pro Re ( x )> 0 ):

Besselovy funkce lze popsat jako Fourierovy transformace mocnin kvadratických funkcí. Například:

Lze to prokázat ukázkou rovnosti s výše uvedenou integrální definicí pro K 0 . To se provádí integrací uzavřené křivky v prvním kvadrantu komplexní roviny.
Upravené Besselovy funkce K 1/3 a K 2/3 lze znázornit pomocí rychle konvergentních integrálů

Modifikované Besselovy funkce druhého druhu byl také nazýván těmito názvy (nyní vzácný):
Sférické Besselovy funkce: j n , y n
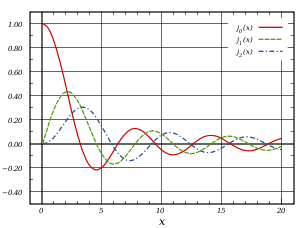
Sférické Besselovy funkce prvního druhu,
j n ( x ) , pro
n = 0, 1, 2
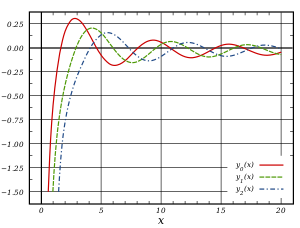
Sférické Besselovy funkce druhého druhu,
y n ( x ) , pro
n = 0, 1, 2
Při řešení Helmholtzovy rovnice v sférických souřadnicích oddělením proměnných má radiální rovnice tvar

Dvě lineárně nezávislá řešení této rovnice se nazývá sférické Besselovy funkce j n a y n , a jsou spojeny s běžnými Besselovy funkce J n a Y n podle

y n je také označeno n n nebo η n ; někteří autoři nazývají tyto funkce sférické Neumannovy funkce .
Sférické Besselovy funkce lze také zapsat jako ( Rayleighovy vzorce )

Nulová sférická Besselova funkce j 0 ( x ) je také známá jako (nenormalizovaná) sinc funkce . Prvních několik sférických Besselových funkcí je:

a

Generující funkce
Sférické Besselovy funkce mají generující funkce

Diferenciální vztahy
V následujícím textu je f n libovolné z j n , y n , h(1)
č, h(2)
čpro n = 0, ± 1, ± 2, ...

Sférické Hankelovy funkce: h(1)
č, h(2)
č
Existují také sférické analogie Hankelových funkcí:

Ve skutečnosti existují jednoduché výrazy v uzavřené formě pro Besselovy funkce polovičního čísla , pokud jde o standardní goniometrické funkce , a tedy pro sférické Besselovy funkce. Zejména pro nezáporná celá čísla n :

a h(2)
čje komplexní konjugát tohoto (pro skutečné x ). Z toho například vyplývá, že j 0 ( x ) =hřích x/Xa y 0 ( x ) = -cos x/X, a tak dále.
Sférické Hankelovy funkce se objevují v problémech zahrnujících šíření sférických vln , například v multipólové expanzi elektromagnetického pole .
Riccati – Besselovy funkce: S n , C n , ξ n , ζ n
Riccatiho -Bessel funguje jen nepatrně liší od sférických funkcí Bessel:

Splňují diferenciální rovnici

Například tento druh diferenciální rovnice se objevuje v kvantové mechanice při řešení radiální složky Schrödingerovy rovnice s hypotetickou válcovou nekonečnou bariérou potenciálu. Tato diferenciální rovnice a řešení Riccati – Bessel také vzniká v problému rozptylu elektromagnetických vln koulí, známého jako Mieův rozptyl po prvním publikovaném řešení Mie (1908). Nedávný vývoj a reference viz např. Du (2004).
Po Debye (1909), notaci ln n , χ n je někdy používán místo S n , C n .
Asymptotické formy
Besselovy funkce mají následující asymptotické formy. Pro malé argumenty 0 < z ≪ √ α + 1 získáme, když α není záporné celé číslo:

Když α je záporné celé číslo, máme

Pro Besselovu funkci druhého druhu máme tři případy:

kde γ je Eulerova – Mascheroniho konstanta (0,5772 ...).
Pro velké skutečné argumenty z ≫ | α 2 -1/4| „Nelze napsat skutečnou asymptotickou formu pro Besselovy funkce prvního a druhého druhu (pokud α není poloviční číslo ), protože mají nuly až do nekonečna, které by musely být přesně shodné s jakoukoli asymptotickou expanzí. Pro danou hodnotu arg z však lze napsat rovnici obsahující termín řádu | z | −1 :

(Pro α =1/2poslední výrazy v těchto vzorcích úplně vypadnou; viz výše uvedené sférické Besselovy funkce.) Přestože jsou tyto rovnice pravdivé, pro komplexní z mohou být k dispozici lepší aproximace . Například J 0 ( z ), když je z blízko záporné reálné čáry, se lépe aproximuje o

než tím

Asymptotické formy pro Hankelovy funkce jsou:

Ty lze rozšířit na další hodnoty arg z pomocí rovnic vztahujících se k H(1)
α( ze im π ) a H(2)
α( ze im π ) do H(1)
α( z ) a H(2)
α( z ) .
Je zajímavé, že ačkoliv je Besselova funkce prvního druhu průměrem obou Hankelských funkcí, J α ( z ) není asymptotická k průměru těchto dvou asymptotických forem, když z je záporné (protože jedna nebo druhá nebude tam, v závislosti na použitém arg z ). Ale asymptotické formy pro Hankelovy funkce nám umožňují psát asymptotické formy pro Besselovy funkce prvního a druhého druhu pro komplexní (nereálné) z , pokud | z | jde do nekonečna při konstantním fázovém úhlu arg z (pomocí odmocniny s kladnou skutečnou částí):

Pro modifikované Besselovy funkce vyvinul Hankel také asymptotická (velká argumentační) rozšíření :

Existuje také asymptotická forma (pro velké reálné )

![{\ Displaystyle {\ begin {aligned} I _ {\ alpha} (z) = {\ frac {1} {{\ sqrt {2 \ pi z}} {\ sqrt [{4}] {1+{\ frac { \ alpha ^{2}} {z ^{2}}}}}}} \ exp \ left (-\ alpha \ operatorname {arsinh} \ left ({\ frac {\ alpha} {z}} \ right)+ z {\ sqrt {1+{\ frac {\ alpha ^{2}} {z ^{2}}}}} \ right) \ left (1+O \ left ({\ frac {1} {z {\ sqrt {1+{\ frac {\ alpha ^{2}} {z ^{2}}}}}}} \ right) \ right). \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e8dffc51e4f1eb138fc189cc6349721add2bb02)
Když α =1/2, všechny podmínky kromě prvního zmizí, a máme

Pro malé argumenty 0 <| z | ≪ √ α + 1 , máme

Plné doménové aproximace s elementárními funkcemi
Velmi dobré aproximace (chyba pod maximální hodnotou 1) Besselovy funkce pro libovolnou hodnotu argumentu x lze dosáhnout pomocí elementárních funkcí spojením trigonometrické aproximace pracující pro menší hodnoty x s výrazem obsahujícím oslabenou kosinusovou funkci platí pro velké argumenty s využitím funkce hladkého přechodu, tj



![{\ Displaystyle J_ {0} (x) \ cca \ left [{\ frac {1} {6}}+{\ frac {1} {3}} \ cos {\ frac {x} {2}}+{ \ frac {1} {3}} \ cos {\ frac {{\ sqrt {3}} x} {2}}+{\ frac {1} {6}} \ cos x \ right] {\ frac {1 } {1+ (x/7)^{20}}}+{\ sqrt {\ frac {2} {\ pi | x |}}} \ cos \ left [x-{\ frac {\ pi} {4 }} \ operatorname {sgn} (x) \ right] \ left [1-{\ frac {1} {1+ (x/7)^{20}}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07df886d28fae6897c6fa4e420bfa2850ea3718c)
Vlastnosti
Pro celé číslo α = n je J n často definováno pomocí Laurentovy řady pro generující funkci:

přístup, který použil PA Hansen v roce 1843. (To lze zobecnit na neceločíselné pořadí pomocí obrysové integrace nebo jinými metodami.) Dalším důležitým vztahem pro celočíselné řády je Jacobi-Angerova expanze :

a

který se používá k rozšíření rovinné vlny jako součtu válcových vln nebo k nalezení Fourierovy řady tónově modulovaného signálu FM .
Obecněji řečeno, série

se nazývá Neumannova expanze f . Koeficienty pro ν = 0 mají explicitní formu

kde O k je Neumannův polynom .
Vybrané funkce připouštějí zvláštní reprezentaci

s

kvůli vztahu ortogonality

Obecněji řečeno, pokud f má bod odbočky blízko původu takové povahy, že

pak

nebo

kde je Laplaceova transformace z f .

Dalším způsobem, jak definovat Besselovy funkce, je Poissonův reprezentační vzorec a Mehler-Sonine vzorec:
![{\ displaystyle {\ begin {aligned} J _ {\ nu} (z) & = {\ frac {\ left ({\ frac {z} {2}} \ right)^{\ nu}} {\ Gamma \ left (\ nu +{\ frac {1} {2}} \ right) {\ sqrt {\ pi}}}} \ int _ {-1}^{1} e^{izs} \ left (1-s^ {2} \ right)^{\ nu -{\ frac {1} {2}}} \, ds \\ [5px] & = {\ frac {2} {{\ left ({\ frac {z} { 2}} \ right)}^{\ nu} \ cdot {\ sqrt {\ pi}} \ cdot \ Gamma \ left ({\ frac {1} {2}}-\ nu \ right)}} \ int _ {1}^{\ infty} {\ frac {\ sin zu} {\ left (u^{2} -1 \ right)^{\ nu +{\ frac {1} {2}}}}} \, du \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248363b3af99701e32dcec48127f0dfc6e7586bf)
kde ν> -1/2a z ∈ C . Tento vzorec je užitečný zejména při práci s Fourierovými transformacemi .
Protože se Besselova rovnice stává hermitovskou (samodružnou), pokud je dělena x , musí řešení splňovat vztah ortogonality pro příslušné okrajové podmínky. Z toho zejména vyplývá, že:
![{\ Displaystyle \ int _ {0}^{1} xJ _ {\ alpha} \ left (xu _ {\ alpha, m} \ right) J _ {\ alpha} \ left (xu _ {\ alpha, n} \ right) \ , dx = {\ frac {\ delta _ {m, n}} {2}} \ left [J _ {\ alpha +1} \ left (u _ {\ alpha, m} \ right) \ right]^{2} = {\ frac {\ delta _ {m, n}} {2}} \ left [J _ {\ alpha} '\ left (u _ {\ alpha, m} \ right) \ right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4901ce8ec95f647c69297f8a6a92d245466ba632)
kde α > -1 , δ m , n je Kroneckerovo delta , a u alfa , m je m th nulu z J- alfa ( x ) . Tento vztah ortogonality pak lze použít k extrakci koeficientů v řadě Fourier – Bessel , kde je funkce rozšířena na základě funkcí J α ( x u α , m ) pro pevné α a měnící se m .
Analogický vztah pro sférické Besselovy funkce následuje okamžitě:
![{\ Displaystyle \ int _ {0}^{1} x^{2} j _ {\ alpha} \ left (xu _ {\ alpha, m} \ right) j _ {\ alpha} \ left (xu _ {\ alpha, n } \ right) \, dx = {\ frac {\ delta _ {m, n}} {2}} \ left [j _ {\ alpha +1} \ left (u _ {\ alpha, m} \ right) \ right ]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de6fbc1b8ac85fb7dd6253a931d1b78cec9b89ae)
Jestliže jeden definuje boxcar funkci z x , která závisí na malém parametru e jako:

(kde rect je funkce obdélníku ), pak Hankelova transformace (libovolného pořadí α > -1/2), g ε ( k ) , se blíží k J α ( k ), jak se ε blíží nule, pro jakékoli dané k . Naopak Hankelova transformace (stejného řádu) g ε ( k ) je f ε ( x ) :

což je nula všude kromě blízko 1. Jak se ε blíží nule, pravá strana se blíží k δ ( x -1) , kde δ je Diracova delta funkce . To připouští limit (v distribučním smyslu):

Změna proměnných pak poskytne uzavírací rovnici :

pro α > -1/2. Hankelova transformace může vyjadřovat docela libovolnou funkci jako integrál Besselových funkcí různých měřítek. Pro sférické Besselovy funkce je vztah ortogonality:

pro α > −1 .
Další důležitá vlastnost Besselových rovnic, která vyplývá z Abelovy identity , zahrnuje wronské řešení:

kde α a B α jsou jakékoliv dvě řešení Besselovy rovnice, a C α je konstantní nezávisle na x (v závislosti na a a na konkrétních Besselovy funkce považovány). Zejména,

a

pro α > −1 .
Pro α > −1 má sudá celá funkce rodu 1, x - α J α ( x ) pouze skutečné nuly. Nechat

tedy všechny jeho kladné nuly

(Existuje velké množství dalších známých integrálů a identit, které zde nejsou reprodukovány, ale které lze nalézt v referencích.)
Vztahy s opakováním
Funkce J α , Y α , H(1)
αa H.(2)
αvšechny splňují relace opakování

a

kde Z označuje J , Y , H (1) nebo H (2) . Tyto dvě identity jsou často kombinovány, např. Sčítány nebo odčítány, aby se získaly různé další vztahy. Tímto způsobem lze například vypočítat Besselovy funkce vyšších řádů (nebo vyšších derivátů) vzhledem k hodnotám nižších řádů (nebo nižších derivací). Z toho zejména vyplývá
![{\ displaystyle {\ begin {aligned} \ left ({\ frac {1} {x}} {\ frac {d} {dx}} \ right)^{m} \ left [x^{\ alpha} Z_ { \ alpha} (x) \ right] & = x^{\ alpha -m} Z _ {\ alpha -m} (x), \\\ left ({\ frac {1} {x}} {\ frac {d } {dx}} \ right)^{m} \ left [{\ frac {Z _ {\ alpha} (x)} {x^{\ alpha}}} \ right] & = (-1)^{m} {\ frac {Z _ {\ alpha +m} (x)} {x^{\ alpha +m}}}. \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59565e99a36cfef8426d543521d8e4df7bc07a2)
Modifikované Besselovy funkce sledují podobné vztahy:

a

a

Relace opakování čte

kde C α označuje I α nebo e αi π K α . Tyto relace opakování jsou užitečné pro diskrétní problémy s difúzí.
Násobící věta
Besselovy funkce se řídí multiplikační větou

kde λ a ν lze brát jako libovolná komplexní čísla. Pro | λ 2 - 1 | <1 , výše uvedený výraz platí také v případě, J nahrazuje Y . Analogické identity pro upravené Besselovy funkce a | λ 2 - 1 | <1 jsou

a

Nuly Besselovy funkce
Bourgetova hypotéza
Sám Bessel původně dokázal, že pro nezáporná celá čísla n má rovnice J n ( x ) = 0 nekonečný počet řešení v x . Když jsou však funkce J n ( x ) vyneseny do stejného grafu, zdá se, že žádná z nul se neshoduje pro různé hodnoty n kromě nuly v x = 0 . Tento jev je známý jako Bourgetova hypotéza podle francouzského matematika 19. století, který studoval Besselovy funkce. Konkrétně uvádí, že pro všechna celá čísla n ≥ 0 a m ≥ 1 nemají funkce J n ( x ) a J n + m ( x ) žádné společné nuly kromě té v x = 0 . Hypotézu dokázal v roce 1929 Carl Ludwig Siegel .
Numerické přístupy
Číselné studie o nulách Besselovy funkce viz Gil, Segura & Temme (2007) , Kravanja et al. (1998) a Moler (2004) .
Viz také
Poznámky
Reference
-
Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [červen 1964]. „Kapitola 9“ . Příručka matematických funkcí se vzorci, grafy a matematickými tabulkami . Řada aplikované matematiky. 55 (Devátý dotisk s dalšími opravami desátého originálního tisku s opravami (prosinec 1972); první vydání). Washington DC; New York: Ministerstvo obchodu USA, National Bureau of Standards; Dover Publications. s. 355, 435. ISBN 978-0-486-61272-0. LCCN 64-60036 . MR 0167642 . LCCN 65-12253 . Viz také kapitola 10 .
-
Arfken, George B. a Hans J. Weber, Mathematical Methods for Physicists , 6. vydání (Harcourt: San Diego, 2005). ISBN 0-12-059876-0 .
- Bowman, Frank Úvod do Besselových funkcí (Dover: New York, 1958). ISBN 0-486-60462-4 .
-
Mie, G. (1908). „Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen“ . Annalen der Physik . 25 (3): 377. Bibcode : 1908AnP ... 330..377M . doi : 10.1002/andp.19083300302 .
-
Olver, FWJ ; Maximon, LC (2010), „Besselova funkce“ , v Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
-
Stiskněte, WH ; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), „Oddíl 6.5. Besselovy funkce celočíselného řádu“ , Numerical Recipes: The Art of Scientific Computing (3. vyd.), New York: Cambridge University Press, ISBN 978-0-521-88068-8.
- B Španělsko, MG Smith, Funkce matematické fyziky , Van Nostrand Reinhold Company, London, 1970. Kapitola 9 se zabývá Besselovými funkcemi.
- NM Temme, speciální funkce. Úvod do klasických funkcí matematické fyziky , John Wiley and Sons, Inc., New York, 1996. ISBN 0-471-11313-1 . Kapitola 9 se zabývá Besselovými funkcemi.
-
Watson, GN , Pojednání o teorii Besselových funkcí, druhé vydání , (1995) Cambridge University Press. ISBN 0-521-48391-3 .
-
Weber, H. (1873), „Ueber eine Darstellung willkürlicher Functionen durch Bessel'sche Functionen“, Mathematische Annalen , 6 (2): 146–161, doi : 10.1007/BF01443190 , S2CID 122409461.
-
Gil, A .; Segura, J .; Temme, NM (2007). Numerické metody pro speciální funkce . Společnost pro průmyslovou a aplikovanou matematiku.
-
Kravanja, P .; Ragos, O .; Vrahatis, MN; Zafiropoulos, FA (1998), „ZEBEC: Matematický softwarový balíček pro výpočet jednoduchých nul Besselových funkcí skutečného řádu a komplexního argumentu“, Computer Physics Communications , 113 (2–3): 220–238, Bibcode : 1998CoPhC.113. 0,220 K , doi : 10,1016/S0010-4655 (98) 00064-2.
externí odkazy
-
Lizorkin, PI (2001) [1994], „Besselovy funkce“ , encyklopedie matematiky , EMS Press.
-
Karmazina, LN; Prudnikov, AP (2001) [1994], „Cylinder function“ , Encyclopedia of Mathematics , EMS Press.
-
Rozov, N. Kh. (2001) [1994], „Besselova rovnice“ , encyklopedie matematiky , EMS Press.
- Stránky funkce Wolfram na Bessel J a Y funkce a modifikovaných Bessel I a K funkcí. Stránky obsahují vzorce, hodnotitele funkcí a kalkulačky vykreslování.
-
Wolfram Mathworld - Besselovy funkce prvního druhu .
- Besselovy funkce J ν , Y ν , I ν a K ν v příručce Librow Function .
- FWJ Olver, LC Maximon, Bessel Functions (kapitola 10 Digitální knihovny matematických funkcí).
-
Moler, CB (2004). Numerické výpočty s MATLABem (PDF) . Společnost pro průmyslovou a aplikovanou matematiku. Archivováno z originálu (PDF) 8. srpna 2017.






























































![{\ Displaystyle {\ begin {aligned} I _ {\ alpha} (z) = {\ frac {1} {{\ sqrt {2 \ pi z}} {\ sqrt [{4}] {1+{\ frac { \ alpha ^{2}} {z ^{2}}}}}}} \ exp \ left (-\ alpha \ operatorname {arsinh} \ left ({\ frac {\ alpha} {z}} \ right)+ z {\ sqrt {1+{\ frac {\ alpha ^{2}} {z ^{2}}}}} \ right) \ left (1+O \ left ({\ frac {1} {z {\ sqrt {1+{\ frac {\ alpha ^{2}} {z ^{2}}}}}}} \ right) \ right). \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e8dffc51e4f1eb138fc189cc6349721add2bb02)





![{\ Displaystyle J_ {0} (x) \ cca \ left [{\ frac {1} {6}}+{\ frac {1} {3}} \ cos {\ frac {x} {2}}+{ \ frac {1} {3}} \ cos {\ frac {{\ sqrt {3}} x} {2}}+{\ frac {1} {6}} \ cos x \ right] {\ frac {1 } {1+ (x/7)^{20}}}+{\ sqrt {\ frac {2} {\ pi | x |}}} \ cos \ left [x-{\ frac {\ pi} {4 }} \ operatorname {sgn} (x) \ right] \ left [1-{\ frac {1} {1+ (x/7)^{20}}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07df886d28fae6897c6fa4e420bfa2850ea3718c)












![{\ displaystyle {\ begin {aligned} J _ {\ nu} (z) & = {\ frac {\ left ({\ frac {z} {2}} \ right)^{\ nu}} {\ Gamma \ left (\ nu +{\ frac {1} {2}} \ right) {\ sqrt {\ pi}}}} \ int _ {-1}^{1} e^{izs} \ left (1-s^ {2} \ right)^{\ nu -{\ frac {1} {2}}} \, ds \\ [5px] & = {\ frac {2} {{\ left ({\ frac {z} { 2}} \ right)}^{\ nu} \ cdot {\ sqrt {\ pi}} \ cdot \ Gamma \ left ({\ frac {1} {2}}-\ nu \ right)}} \ int _ {1}^{\ infty} {\ frac {\ sin zu} {\ left (u^{2} -1 \ right)^{\ nu +{\ frac {1} {2}}}}} \, du \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248363b3af99701e32dcec48127f0dfc6e7586bf)
![{\ Displaystyle \ int _ {0}^{1} xJ _ {\ alpha} \ left (xu _ {\ alpha, m} \ right) J _ {\ alpha} \ left (xu _ {\ alpha, n} \ right) \ , dx = {\ frac {\ delta _ {m, n}} {2}} \ left [J _ {\ alpha +1} \ left (u _ {\ alpha, m} \ right) \ right]^{2} = {\ frac {\ delta _ {m, n}} {2}} \ left [J _ {\ alpha} '\ left (u _ {\ alpha, m} \ right) \ right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4901ce8ec95f647c69297f8a6a92d245466ba632)
![{\ Displaystyle \ int _ {0}^{1} x^{2} j _ {\ alpha} \ left (xu _ {\ alpha, m} \ right) j _ {\ alpha} \ left (xu _ {\ alpha, n } \ right) \, dx = {\ frac {\ delta _ {m, n}} {2}} \ left [j _ {\ alpha +1} \ left (u _ {\ alpha, m} \ right) \ right ]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de6fbc1b8ac85fb7dd6253a931d1b78cec9b89ae)












![{\ displaystyle {\ begin {aligned} \ left ({\ frac {1} {x}} {\ frac {d} {dx}} \ right)^{m} \ left [x^{\ alpha} Z_ { \ alpha} (x) \ right] & = x^{\ alpha -m} Z _ {\ alpha -m} (x), \\\ left ({\ frac {1} {x}} {\ frac {d } {dx}} \ right)^{m} \ left [{\ frac {Z _ {\ alpha} (x)} {x^{\ alpha}}} \ right] & = (-1)^{m} {\ frac {Z _ {\ alpha +m} (x)} {x^{\ alpha +m}}}. \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59565e99a36cfef8426d543521d8e4df7bc07a2)






