Soudržný stav - Coherent state

V fyziky , konkrétně v kvantové mechaniky , je soudržný stát je specifická kvantový stav na quantum harmonický oscilátor , často popisován jako stav, který má dynamiku nejpodobnějších oscilačního chování klasické harmonický oscilátor . Byl to první příklad kvantové dynamiky, když ji v roce 1926 odvodil Erwin Schrödinger , když hledal řešení Schrödingerovy rovnice, která splňují princip korespondence . Kvantový harmonický oscilátor (a tedy i koherentní stavy) vznikají v kvantové teorii široké škály fyzikálních systémů. Například koherentní stav popisuje oscilační pohyb částice omezené v kvadratické potenciálové jámě (pro časný odkaz viz např. Schiffova učebnice). Koherentní stav popisuje stav v systému, pro který je vlněný balíček základního stavu přemístěn od počátku systému. Tento stav může souviset s klasickými řešeními pomocí částice kmitající s amplitudou ekvivalentní posunutí.

Tyto stavy, vyjádřené jako vektorů na snižování provozovatele a tvořící overcomplete rodinu, byl představen v časných prací z John R. Klauder , například v kvantové teorie světla ( kvantové elektrodynamiky ) a další Bosonic teorií kvantové pole , byly zavedeny koherentní stavy prací Roye J. Glaubera v roce 1963 a jsou také známé jako státy Glauber .

Koncept koherentních států byl značně abstrahován; to se stalo hlavním tématem v matematické fyzice a v aplikované matematice , s aplikacemi od kvantování po zpracování signálu a zpracování obrazu (viz Koherentní stavy v matematické fyzice ). Z tohoto důvodu jsou koherentní stavy spojené s kvantovým harmonickým oscilátorem někdy označovány jako kanonické koherentní stavy (CCS), standardní koherentní stavy , Gaussovy stavy nebo stavy oscilátoru.

Koherentní stavy v kvantové optice

Obrázek 1: Elektrické pole měřené optickou homodynovou detekcí jako funkce fáze pro tři koherentní stavy vyzařované laserem Nd: YAG. Množství kvantového šumu v elektrickém poli je zcela nezávislé na fázi. Jak se zvyšuje intenzita pole, tj. Amplituda oscilace α koherentního stavu, je kvantový šum nebo nejistota konstantní na 1/2, a tak se stává méně a méně významným. V limitu velkého pole se stav stává dobrou aproximací bezhlučné stabilní klasické vlny. Průměrné počty fotonů ze tří stavů shora dolů jsou ⟨n⟩ = 4,2, 25,2, 924,5

Obrázek 2: Oscilační vlnový paket odpovídající druhému koherentnímu stavu znázorněnému na obrázku 1. V každé fázi světelného pole je distribuce Gaussian s konstantní šířkou.

Obrázek 3: Wignerova funkce koherentního stavu znázorněného na obrázku 2. Distribuce je soustředěna na amplitudu stavu α a kolem tohoto bodu je symetrická . Vlny jsou způsobeny experimentálními chybami.

V kvantové optice se koherentním stavem rozumí stav kvantovaného elektromagnetického pole atd., Který popisuje maximální druh koherence a klasický druh chování. Erwin Schrödinger ji v roce 1926 odvodil jako Gaussovu vlnovou sadu „minimální nejistoty “ a hledal řešení Schrödingerovy rovnice, která splňují zásadu korespondence . Jedná se o stav minimální nejistoty , přičemž je zvolen jediný volný parametr, aby se relativní disperze (standardní odchylka v přirozených bezrozměrných jednotkách) rovnala poloze a hybnosti, přičemž každý z nich by byl při vysoké energii stejně malý.

Dále, na rozdíl od vlastních energetických stavů systému, je časový vývoj koherentního stavu soustředěn podél klasických trajektorií . Kvantový lineární harmonický oscilátor, a tedy koherentní stavy, vznikají v kvantové teorii široké škály fyzikálních systémů. Vyskytují se v kvantové teorii světla ( kvantová elektrodynamika ) a dalších bosonických kvantových teoriích pole .

I když byla minimální nejistota Gaussových vlnových balíčků dobře známa, nepřitahovaly plnou pozornost, dokud Roy J. Glauber v roce 1963 neposkytl úplný kvantově-teoretický popis koherence v elektromagnetickém poli. V tomto ohledu by neměl být opomenut souběžný příspěvek EKG Sudarshan , (v Glauberově článku je však poznámka, která zní: „Použití těchto států jako generujících funkcí pro -kvantové státy však učinil J. Schwinger). Glauber byl k tomu vyzván, aby poskytl popis experimentu Hanbury-Brown & Twiss, který generoval velmi široké základní interferenční vzory (stovky nebo tisíce mil), které by mohly být použity k určení hvězdných průměrů. Tím se otevřely dveře mnohem komplexnější pochopení koherence. (Další informace najdete v kvantově mechanickém popisu .) ${\ displaystyle n}$

V klasické optice je světlo považováno za elektromagnetické vlny vyzařující ze zdroje. Koherentní laserové světlo je často považováno za světlo vyzařované mnoha zdroji, které jsou ve fázi . Ve skutečnosti není obraz jednoho fotonu ve fázi s druhým v kvantové teorii platný. Laserové záření je produkováno v rezonanční dutině, kde rezonanční frekvence dutiny je stejná jako frekvence spojená s přechody atomových elektronů zajišťujících tok energie do pole. Jak se energie v rezonančním režimu hromadí, zvyšuje se pravděpodobnost stimulované emise pouze v tomto režimu. Jedná se o smyčku pozitivní zpětné vazby, ve které se amplituda v rezonančním režimu exponenciálně zvyšuje, dokud ji nelineární efekty neomezují. Jako protiklad například žárovka vyzařuje světlo do kontinua režimů a neexistuje nic, co by vybíralo jeden režim nad druhým. Emisní proces je v prostoru a čase vysoce náhodný (viz tepelné světlo ). V laseru je však světlo emitováno do rezonančního režimu a tento režim je vysoce koherentní . Laserové světlo je tedy idealizováno jako koherentní stav. (Klasicky takový stav popisujeme elektrickým polem kmitajícím jako stabilní vlna. Viz obr.1)

Kromě popisu laserů se koherentní stavy chovají také pohodlně při popisu kvantového působení rozdělovačů paprsků : dva vstupní paprsky koherentního stavu se jednoduše převedou na dva paprsky koherentního stavu na výstupu s novými amplitudami danými klasickými vzorci elektromagnetických vln; takové jednoduché chování se u ostatních vstupních stavů, včetně stavů čísel, nevyskytuje. Podobně pokud je svazek paprsků koherentního stavu částečně absorbován, pak zbytek je čistý koherentní stav s menší amplitudou, zatímco částečná absorpce světla nekoherentního stavu vytváří komplikovanější statistický smíšený stav . Termální světlo lze popsat jako statistickou směs koherentních stavů a typickým způsobem definování neklasického světla je, že jej nelze popsat jako jednoduchou statistickou směs koherentních stavů.

Energetické vlastní stavy lineárního harmonického oscilátoru (např. Hmoty na pružinách, mřížkové vibrace v pevné látce, vibrační pohyby jader v molekulách nebo oscilace v elektromagnetickém poli) jsou kvantové stavy s pevným počtem. Stav Fock (např jediný foton) je nejvíce částic podobného stavu; má stálý počet částic a fáze je neurčitá. Koherentní stav rozděluje svou kvantově-mechanickou nejistotu rovnoměrně mezi kanonicky konjugované souřadnice , polohu a hybnost a relativní nejistota ve fázi [definovaná heuristicky ] a amplituda jsou zhruba stejné - a malé při vysoké amplitudě.

Kvantová mechanická definice

Matematicky je koherentní stav definován jako (jedinečný) vlastní stav vyhlazovacího operátoru $â$ s odpovídající vlastní hodnotou $α$ . Formálně to zní: ${\ displaystyle | \ alpha \ rangle}$

{\ displaystyle {\ hat {a}} | \ alpha \ rangle = \ alpha | \ alpha \ rangle ~.}

Protože $â$ není poustevník , $α$ je obecně komplexní číslo. Psaní | $α$ | a $θ$ se nazývají amplituda a fáze stavu . ${\ displaystyle \ alpha = | \ alpha | e ^ {i \ theta},}$ ${\ displaystyle | \ alpha \ rangle}$

Stát se v literatuře nazývá kanonický koherentní stav , protože existuje mnoho dalších typů koherentních stavů, jak je vidět v doprovodném článku Koherentní stavy v matematické fyzice . ${\ displaystyle | \ alpha \ rangle}$

Fyzikálně tento vzorec znamená, že koherentní stav zůstává nezměněn anihilací buzení pole, nebo řekněme částice. Vlastní stav provozovatele anihilace má distribuci Poissonian čísla, když je vyjádřen na základě energetických vlastních stavů, jak je uvedeno níže. Poissonovo rozdělení je nutný a postačující podmínkou, že všechny detekce jsou statisticky nezávislé. Porovnejte to se stavem jedné částice (stav Fock ): jakmile je detekována jedna částice, je nulová pravděpodobnost detekce další. ${\ displaystyle | 1 \ rangle}$

Původ tohoto využijí (netradičně normalizovány) operátorů bezrozměrné , $X$ a $P$ , které se běžně nazývají pole kvadratur v kvantové optice. (Viz Nedimenzionalizace .) Tyto operátory souvisejí s operátory polohy a hybnosti hmotnosti $m$ na pružině s konstantou $k$ ,

{\ displaystyle {P} = {\ sqrt {\ frac {1} {2 \ hbar m \ omega}}} \ {\ hat {p}} {\ text {,}} \ quad {X} = {\ sqrt {\ frac {m \ omega} {2 \ hbar}}} \ {\ hat {x}} {\ text {,}} \ quad \ quad {\ text {kde}} \ omega \ equiv {\ sqrt {k / m}} ~.}

Obrázek 4: Pravděpodobnost detekce n fotonů, distribuce počtu fotonů, koherentního stavu na obrázku 3. Jak je nutné pro Poissonovo rozdělení, střední číslo fotonu se rovná rozptylu distribuce počtu fotonů. Sloupce odkazují na teorii, tečky na experimentální hodnoty.

Pro optického pole ,

{\ displaystyle ~ E _ {\ rm {R}} = \ vlevo ({\ frac {2 \ hbar \ omega} {\ epsilon _ {0} V}} \ vpravo) ^ {1/2} \! \! \ ! \ cos (\ theta) X \ qquad {\ text {a}} \ qquad ~ E _ {\ rm {I}} = \ left ({\ frac {2 \ hbar \ omega} {\ epsilon _ {0} V }} \ vpravo) ^ {1/2} \! \! \! \ sin (\ theta) X ~}

jsou skutečné a imaginární složky režimu elektrického pole uvnitř dutiny objemu . ${\ displaystyle V}$

S těmito (bezrozměrnými) operátory se Hamiltonian obou systémů stává

{\ displaystyle {H} = \ hbar \ omega \ left ({P} ^ {2} + {X} ^ {2} \ right) {\ text {,}} \ qquad {\ text {with}} \ qquad \ left [{X}, {P} \ right] \ equiv {XP} - {PX} = {\ frac {i} {2}} \, {I}.}

Erwin Schrödinger hledal nejklasičtější státy, když poprvé představil minimální nejistotu Gaussových vlnových paketů. Kvantový stav harmonického oscilátoru, který minimalizuje vztah nejistoty s nejistotou rovnoměrně rozložen mezi $X$ a $P$ splňuje rovnice

{\ displaystyle \ left ({X} - \ langle {X} \ rangle \ right) \, | \ alpha \ rangle = -i \ left ({P} - \ langle {P} \ rangle \ right) \, | \ alpha \ rangle {\ text {,}}}

nebo ekvivalentně

{\ displaystyle \ left ({X} + i {P} \ right) \, \ left | \ alpha \ right \ rangle = \ left \ langle {X} + i {P} \ right \ rangle \, \ left | \ alpha \ right \ rangle ~,}

a tudíž

{\ displaystyle \ langle \ alpha \! \ mid \ left ({X} - \ langle X \ rangle \ right) ^ {2} + \ left ({P} - \ langle P \ rangle \ right) ^ {2} \ mid \! \ alpha \ rangle = 1/2 ~.}

Vzhledem k $(∆ X ∆ (P) ² \geq 0 tedy$ Schrödinger zjistil, že stavy minimální nejistoty pro lineární harmonický oscilátor jsou vlastní stavy $(X + iP)$ . Protože â je $(X + iP)$ , lze jej ve smyslu výše uvedené definice rozpoznat jako koherentní stav.

Glauber pomocí notace pro stavy více fotonů charakterizoval stav úplné koherence všech řádů v elektromagnetickém poli jako vlastní stav vyhlazovacího operátora - formálně v matematickém smyslu stejný stav, jaký našel Schrödinger. Název soudržný stát se ujal po práci Glaubera.

Pokud je nejistota minimalizována, ale nemusí být nutně stejně vyvážená mezi $X$ a $P$ , stav se nazývá vymačkaný koherentní stav .

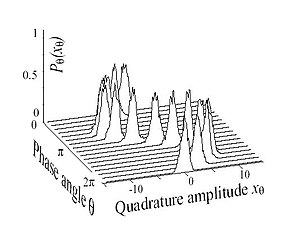
Umístění koherentního stavu v komplexní rovině ( fázový prostor ) je vystředěno v poloze a hybnosti klasického oscilátoru fáze $θ$ a amplitudy | α | dáno vlastním číslem α (nebo stejnou komplexní hodnotou elektrického pole pro elektromagnetickou vlnu). Jak je znázorněno na obrázku 5, nejistota, stejně šíří do všech směrů, je reprezentován kotouče o průměru 1 / 2 . Jak se fáze mění, koherentní stavové kruhy kolem počátku a disk se nezkreslí ani nerozšíří. Toto je nejpodobnější kvantový stav jednomu bodu ve fázovém prostoru.

Obrázek 5: Fázový prostorový diagram koherentního stavu. To ukazuje, že nejistota v koherentním stavu je rovnoměrně rozložena ve všech směrech. Vodorovná a svislá osa jsou kvadratury pole X a P (viz text). Červené tečky na ose x sledují hranice kvantového šumu na obrázku 1. Podrobněji viz odpovídající obrázek formulace fázového prostoru .

Vzhledem k tomu, nejistota (a tudíž pro měření hluku) zůstává konstantní na 1 / 2, jako amplituda zvyšuje kmitání, státní chová více jako sinusové vlny, jak je znázorněno na obrázku 1. Kromě toho, protože podtlak stav je jen soudržný stát s $α$ = 0, všechny koherentní stavy mají stejnou nejistotu jako vakuum. Proto lze interpretovat kvantový šum koherentního stavu jako způsobený fluktuacemi vakua. ${\ displaystyle | 0 \ rangle}$

Zápis neodkazuje na Fockův stav . Například když $α$ = 1, neměli bychom se mýlit se stavem Fock s jedním fotonem, který je také označen jeho vlastní notací. Výraz s $α$ = 1 představuje Poissonovo rozdělení stavů čísel se středním počtem fotonů jednoty. ${\ displaystyle | \ alpha \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | \ alpha \ rangle}$ ${\ displaystyle | n \ rangle}$

Formálním řešením rovnice vlastních čísel je vakuový stav přemístěný do polohy $α$ ve fázovém prostoru, tj. Je získán tak, že operátor jednotkového posunutí $D (α)$ pracuje na vakuu,

{\ displaystyle | \ alpha \ rangle = e ^ {\ alpha {\ hat {a}} ^ {\ dagger} - \ alpha ^ {*} {\ hat {a}}} | 0 \ rangle = D (\ alpha ) | 0 \ rangle}

,

kde $â = X + iP$ a $â † = X-iP$ .

To lze snadno vidět, stejně jako prakticky všechny výsledky zahrnující koherentní stavy, za použití reprezentace koherentního stavu na základě Fockových stavů,

{\ displaystyle | \ alpha \ rangle = e ^ {- {| \ alpha | ^ {2} \ nad 2}} \ sum _ {n = 0} ^ {\ infty} {\ alpha ^ {n} \ nad { \ sqrt {n!}}} | n \ rangle = e ^ {- {| \ alpha | ^ {2} \ nad 2}} e ^ {\ alpha {\ hat {a}} ^ {\ dagger}} e ^ {- {\ alpha ^ {*} {\ hat {a}}}} | 0 \ rangle ~,}

kde jsou energetické (početné) vlastní vektory hamiltoniánu ${\ displaystyle | n \ rangle}$

{\ displaystyle H = \ hbar \ omega ({\ hat {a}} ^ {\ dagger} {\ hat {a}} + {\ frac {1} {2}}) ~.}

Pro odpovídající Poissonovu distribuci je pravděpodobnost detekce $n$ fotonů

{\ displaystyle P (n) = | \ langle n | \ alpha \ rangle | ^ {2} = e ^ {- \ langle n \ rangle} {\ frac {\ langle n \ rangle ^ {n}} {n! }} ~.}

Podobně je průměrný počet fotonů v koherentním stavu

{\ displaystyle ~ \ langle n \ rangle = \ langle {\ hat {a}} ^ {\ dagger} {\ hat {a}} \ rangle = | \ alpha | ^ {2} ~}

a rozptyl je

{\ displaystyle ~ (\ Delta n) ^ {2} = {\ rm {Var}} \ left ({\ hat {a}} ^ {\ dagger} {\ hat {a}} \ right) = | \ alpha | ^ {2} ~}

.

To znamená, že standardní odchylka detekovaného čísla jde jako druhá odmocnina detekovaného čísla. Takže v limitu velkého $α$ jsou tyto detekční statistiky ekvivalentní statistikám klasické stabilní vlny.

Tyto výsledky se vztahují na výsledky detekce u jednoho detektoru a vztahují se tedy ke koherenci prvního řádu (viz stupeň koherence ). U měření, která korelují detekce na více detektorech, je však zahrnuta koherence vyššího řádu (např. Korelace intenzity, koherence druhého řádu, u dvou detektorů). Glauberova definice kvantové koherence zahrnuje korelační funkce n-tého řádu (koherence n-tého řádu) pro všechna $n$ . Dokonalý koherentní stav má všech n-řádů korelace rovných 1 (koherentní). Je dokonale koherentní se všemi objednávkami.

Práce Roye J. Glaubera byla podněcována výsledky Hanbury-Brown a Twiss, které produkovaly interferenční vzory prvního řádu dlouhého doletu (stovky nebo tisíce mil) pomocí kolísání intenzity (nedostatek koherence druhého řádu), s úzkopásmové filtry (částečná koherence prvního řádu) na každém detektoru. (Lze si představit, během velmi krátkých dob, téměř okamžitý interferenční obrazec ze dvou detektorů, kvůli úzkopásmovým filtrům, který náhodně tancuje kvůli měnícímu se relativnímu fázovému rozdílu. S čítačem náhod by taneční interferenční obrazec být silnější v době zvýšené intenzity [společné pro oba paprsky] a tento vzor by byl silnější než hluk pozadí.) Téměř všechny optiky se týkaly koherence prvního řádu. Výsledky Hanbury-Brown a Twiss přiměly Glaubera, aby se podíval na koherenci vyššího řádu, a přišel s úplným kvantově-teoretickým popisem koherence ke všem řádům v elektromagnetickém poli (a kvantově-teoretickým popisem signálu plus šum). . Vytvořil pojem koherentní stav a ukázal, že vznikají při interakci klasického elektrického proudu s elektromagnetickým polem.

V $α ≫ 1$ , z obrázku 5, jednoduchá geometrie dává Δθ | α | = 1/2. Z toho se ukazuje, že existuje kompromis mezi nejistotou čísel a fázovou nejistotou, Δθ Δn = 1/2, což se někdy interpretuje jako vztah nejistoty číselné fáze; ale nejde o formální přísný vztah nejistoty: v kvantové mechanice neexistuje jednoznačně definovaný fázový operátor.

Vlnová funkce koherentního stavu

Časový vývoj rozdělení pravděpodobnosti s kvantovou fází (barvou) koherentního stavu s α = 3.

Pro nalezení vlnové funkce koherentního stavu, Schrödingerovy vlnové sady s minimální nejistotou, je nejjednodušší začít s Heisenbergovým obrazem kvantového harmonického oscilátoru pro koherentní stav . Všimněte si, že ${\ displaystyle | \ alpha \ rangle}$

{\ displaystyle ~ a (t) | \ alpha \ rangle = e ^ {- i \ omega t} a (0) | \ alpha \ rangle}

Koherentní stát je vlastním stavem vyhlazovacího operátora na Heisenbergově obrázku .

Je snadné vidět, že na Schrödingerově obrázku je to stejné vlastní číslo

{\ displaystyle ~ \ alpha (t) = e ^ {- i \ omega t} \ alpha (0) ~}

nastane,

{\ displaystyle ~ a | \ alpha (t) \ rangle = \ alpha (t) | \ alpha (t) \ rangle}

.

V souřadnicových reprezentacích vyplývajících z operace by to činilo diferenciální rovnici, ${\ displaystyle \ langle x |}$

{\ displaystyle ~ {\ sqrt {\ frac {m \ omega} {2 \ hbar}}} \ vlevo (x + {\ frac {\ hbar} {m \ omega}} {\ frac {\ částečné} {\ částečné x }} \ right) \ psi ^ {\ alpha} (x, t) = \ alpha (t) \ psi ^ {\ alpha} (x, t) ~,}

který lze snadno vyřešit

{\ displaystyle ~ \ psi ^ {(\ alpha)} (x, t) = \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ right) ^ {1/4} \ exp {\ Bigg (} - {\ frac {m \ omega} {2 \ hbar}} \ vlevo (x - {\ sqrt {\ frac {2 \ hbar} {m \ omega}}} \ Re [\ alpha (t)] \ right) ^ {2} + i {\ sqrt {\ frac {2m \ omega} {\ hbar}}} \ Im [\ alpha (t)] x + i \ theta (t) {\ Bigg)} ~, }

kde $θ (t)$ je dosud neurčená fáze, která má být stanovena požadavkem, aby vlnová funkce splňovala Schrödingerovu rovnici.

Z toho vyplývá, že

{\ displaystyle ~ \ theta (t) = - {\ frac {\ omega t} {2}} + {\ frac {| \ alpha (0) | ^ {2} \ sin (2 \ omega t-2 \ sigma )} {2}} ~, {\ text {kde}} \ qquad \ alpha (0) \ equiv | \ alpha (0) | \ exp (i \ sigma) ~,}

takže $σ$ je počáteční fáze vlastního čísla.

Střední poloha a hybnost tohoto „minimálního Schrödingerova vlnového paketu“ $ψ$ $(α)$ tedy oscilují stejně jako klasický systém ,

${\ displaystyle \ langle {\ hat {x}} (t) \ rangle = {\ sqrt {\ frac {2 \ hbar} {m \ omega}}} \ Re [\ alpha (t)] = | \ alpha ( 0) | {\ sqrt {\ frac {2 \ hbar} {m \ omega}}} \ cos (\ sigma - \ omega t) ~,}$

${\ displaystyle \ langle {\ hat {p}} (t) \ rangle = {\ sqrt {2m \ hbar \ omega}} \ Im [\ alpha (t)] = | \ alpha (0) | {\ sqrt { 2m \ hbar \ omega}} \ sin (\ sigma - \ omega t) ~.}$

Hustota pravděpodobnosti zůstává Gaussianem soustředěným na tento oscilační průměr,

{\ displaystyle | \ psi ^ {(\ alpha)} (x, t) | ^ {2} = {\ sqrt {\ frac {m \ omega} {\ pi \ hbar}}} e ^ {- {\ frac {m \ omega} {\ hbar}} \ left (x- \ langle {\ hat {x}} (t) \ rangle \ right) ^ {2}}.}

Matematické rysy kanonických koherentních stavů

Doposud popsané kanonické koherentní stavy mají tři vlastnosti, které jsou vzájemně ekvivalentní, protože každý z nich zcela specifikuje stav , jmenovitě, ${\ displaystyle | \ alpha \ rangle}$

Jsou to vektory podle provozovatele vyhlazovacího : . ${\ displaystyle {\ hat {a}} | \ alpha \ rangle = \ alpha | \ alpha \ rangle \,}$
Získávají se ze vakua použitím jednotného operátora posunutí : . ${\ displaystyle | \ alpha \ rangle = e ^ {\ alpha {\ hat {a}} ^ {\ dagger} - \ alpha ^ {*} {\ hat {a}}} | 0 \ rangle = D (\ alpha ) | 0 \ rangle \,}$
Jsou to stavy (symetrický) minimální nejistotou: . ${\ displaystyle \ Delta X = \ Delta P = 1/2 \,}$

Každá z těchto vlastností může vést k zevšeobecňování, které se obecně navzájem liší ( některé z nich naleznete v článku „ Koherentní stavy v matematické fyzice “). Zdůrazňujeme, že koherentní stavy mají matematické rysy, které se velmi liší od těch ve Fockově stavu ; například dva různé koherentní stavy nejsou kolmé,

{\ displaystyle \ langle \ beta | \ alpha \ rangle = e ^ {- {1 \ nad 2} (| \ beta | ^ {2} + | \ alpha | ^ {2} -2 \ beta ^ {*} \ alfa)} \ neq \ delta (\ alpha - \ beta)}

(souvisí se skutečností, že jsou vlastní vektory non-self-adjoint vyhlazovacího operátora $AA$ ).

Pokud je tedy oscilátor v kvantovém stavu , je také s nenulovou pravděpodobností v druhém kvantovém stavu (ale čím dále jsou státy umístěny ve fázovém prostoru, tím nižší je pravděpodobnost). Jelikož však poslouchají uzavírací vztah, lze jakýkoli stav rozložit na množinu koherentních stavů. Tvoří tedy nadkompletní základ , ve kterém lze diagonálně rozložit jakýkoli stát. To je předpoklad pro reprezentaci Sudarshan-Glauber P . ${\ displaystyle | \ alpha \ rangle}$ ${\ displaystyle | \ beta \ rangle}$

Tento uzavírací vztah lze vyjádřit rozlišením operátoru identity $I$ ve vektorovém prostoru kvantových stavů,

{\ displaystyle {\ frac {1} {\ pi}} \ int | \ alpha \ rangle \ langle \ alpha | d ^ {2} \ alpha = I \ qquad d ^ {2} \ alpha \ equiv d \ Re ( \ alpha) \, d \ Im (\ alpha) ~.}

Toto rozlišení identity je úzce spojeno s transformací Segal – Bargmann .

Další zvláštností je, že nemá vlastní eket (zatímco $â$ nemá vlastní eigenbra). Následující rovnost je nejbližší formální náhradou a ukazuje se, že je užitečná pro technické výpočty, ${\ displaystyle {\ hat {a}} ^ {\ dagger}}$

{\ displaystyle a ^ {\ dagger} | \ alpha \ rangle = \ left ({\ částečné \ nad \ částečné \ alpha} + {\ alpha ^ {*} \ nad \ alfa} {\ částečné \ nad \ částečné \ alfa ^ {*}} + \ alpha ^ {*} \ vpravo) | \ alpha \ rangle ~.}

Tento poslední stav je znám jako „stav Agarwal“ nebo koherentní stav přidaný fotony a je označen jako ${\ displaystyle | \ alpha, 1 \ rangle.}$

Normalizované stavy Agarwal řádu $n$ lze vyjádřit jako ${\ displaystyle | \ alpha, n \ rangle = [{{\ hat {a}} ^ {\ dagger}]} ^ {n} | \ alpha \ rangle / \ | [{{\ hat {a}} ^ { \ dagger}]} ^ {n} | \ alpha \ rangle \ | ~.}$

Výše uvedené rozlišení identity může být odvozeno (omezeno na jednu prostorovou dimenzi pro jednoduchost) převzetím maticových prvků mezi vlastními stavy polohy , na obou stranách rovnice. Na pravé straně to okamžitě dává $δ (xy)$ . Na levé straně je totéž získáno vložením ${\ displaystyle \ langle x | \ cdots | y \ rangle}$

{\ displaystyle \ psi ^ {\ alpha} (x, t) = \ langle x | \ alpha (t) \ rangle}

z předchozí části (čas je libovolný), pak se integruje přes pomocí Fourierovy znázornění funkce delta , a potom provedením Gaussova integrální Over . ${\ displaystyle \ Im (\ alpha)}$ ${\ displaystyle \ Re (\ alpha)}$

Z explicitní hodnoty vyplývá zejména stav Gaussian Schroedinger wavepacket

{\ displaystyle \ langle x | \ alpha \ rangle = {\ frac {e ^ {- {\ frac {(x - {\ sqrt {2}} \ Re (\ alpha)) ^ {2}} {2}} + ix {\ sqrt {2}} \ Im (\ alpha)}} {\ pi ^ {1/4}}} ~.}

Rozlišení identity může být také vyjádřeno jako poloha částic a hybnost. Pro každou souřadnicovou dimenzi (pomocí upravené notace s novým významem pro ), ${\ displaystyle x}$

{\ displaystyle | \ alpha \ rangle \ equiv | x, p \ rangle \ qquad \ qquad x \ equiv \ langle {\ hat {x}} \ rangle \ qquad \ qquad p \ equiv \ langle {\ hat {p}} \ rangle}

čte uzavírací vztah koherentních stavů

{\ displaystyle I = \ int | x, p \ rangle \, \ langle x, p | ~ {\ frac {\ mathrm {d} x \, \ mathrm {d} p} {2 \ pi \ hbar}} ~ .}

To lze vložit do jakékoli kvantově-mechanické očekávané hodnoty, vztahující se k nějakému kvaziklasickému integrálu fázového prostoru a vysvětlující zejména původ normalizačních faktorů pro klasické dělící funkce v souladu s kvantovou mechanikou. ${\ displaystyle (2 \ pi \ hbar) ^ {- 1}}$

Kromě toho, že je přesným vlastním stavem operátorů zničení, je koherentní stav přibližný společný vlastní stav polohy a hybnosti. Omezení opět na jednu dimenzi,

{\ displaystyle {\ hat {x}} | x, p \ rangle \ cca x | x, p \ rangle \ qquad \ qquad {\ hat {p}} | x, p \ rangle \ cca p | x, p \ zvonit}

Chyba v těchto aproximacích se měří nejistotami polohy a hybnosti,

{\ displaystyle \ langle x, p | \ left ({\ hat {x}} - x \ right) ^ {2} | x, p \ rangle = \ left (\ Delta x \ right) ^ {2} \ qquad \ qquad \ langle x, p | \ left ({\ hat {p}} - p \ right) ^ {2} | x, p \ rangle = \ left (\ Delta p \ right) ^ {2} ~.}

Tepelně koherentní stav

Jediný režim tepelného koherentního stavu se vyrábí přemístěním tepelně smíšeného stavu ve fázovém prostoru , v přímé analogii s posunem stavu vakua, s ohledem na generování koherentního stavu. Matice hustoty koherentního tepelného stavu v reprezentaci operátor přečte

{\ displaystyle \ rho (\ alpha, \ beta) = {\ frac {1} {Z}} D (\ alpha) e ^ {- \ hbar \ beta \ omega a ^ {\ dagger} a} D ^ {\ dýka} (\ alfa),}

kde je operátor posunutí, který generuje koherentní stav se složitou amplitudou , a . Funkce oddílu se rovná ${\ displaystyle D (\ alfa)}$ ${\ displaystyle D (\ alfa) | 0 \ rangle = | \ alpha \ rangle}$ ${\ displaystyle \ alpha}$ ${\ displaystyle \ beta = 1 / (k_ {B} T)}$

{\ displaystyle Z = {\ text {tr}} \ left \ {\ displaystyle e ^ {- \ hbar \ beta \ omega a ^ {\ dagger} a} \ right \} = \ sum _ {n = 0} ^ {\ infty} e ^ {- n \ beta \ hbar \ omega} = {\ frac {1} {1-e ^ {- \ hbar \ beta \ omega}}}}

Pomocí rozšíření provozovatele jednoty v Fock státech , je operátor hustota definice může být vyjádřena ve tvaru ${\ displaystyle I \ equiv \ sum _ {n = 0} ^ {\ infty} | n \ rangle \ langle n |}$

{\ displaystyle \ rho (\ alpha, \ beta) = {\ frac {1} {Z}} \ součet _ {n = 0} ^ {\ infty} e ^ {- n \ hbar \ beta \ omega} D ( \ alpha) | n \ rangle \ langle n | D ^ {\ dagger} (\ alpha) = {\ frac {1} {Z}} \ sum _ {n = 0} ^ {\ infty} e ^ {- n \ hbar \ beta \ omega} | \ alpha, n \ rangle \ langle \ alpha, n |,}

kde znamená vysídlený Fockův stav . Poznamenáváme, že pokud teplota klesne na nulu, máme ${\ displaystyle | \ alpha, n \ rangle}$

{\ displaystyle \ lim _ {\ beta \ to \ infty} \ rho (\ alpha, \ beta) = \ lim _ {\ beta \ to \ infty} \ součet _ {n = 0} ^ {\ infty} e ^ {-n \ hbar \ beta \ omega} (1-e ^ {- \ hbar \ beta \ omega}) | \ alpha, n \ rangle \ langle \ alpha, n | = \ sum _ {n = 0} ^ { \ infty} \ delta _ {n, 0} | \ alpha, n \ rangle \ langle \ alpha, n | = | \ alpha, 0 \ rangle \ langle \ alpha, 0 |,}

což je matice hustoty pro koherentní stav. Průměrný počet fotonů v tomto stavu lze vypočítat níže

{\ displaystyle \ langle n \ rangle = {\ text {Tr}} \ {\ rho a ^ {\ dagger} a \} = {\ frac {1} {Z}} {\ text {Tr}} \ {D ^ {\ dagger} (\ alpha) a ^ {\ dagger} D ({\ alpha}) D ^ {\ dagger} (\ alpha) aD (\ alpha) e ^ {- \ beta \ hbar \ omega a ^ { \ dagger} a} \} = {\ frac {1} {Z}} {\ text {Tr}} \ {(a ^ {\ dagger} + \ alpha ^ {*}) (a + \ alpha) e ^ { - \ beta \ hbar \ omega a ^ {\ dagger} a} \} =}

{\ displaystyle = | \ alpha | ^ {2} {\ frac {1} {Z}} {\ text {Tr}} \ {e ^ {- \ beta \ hbar \ omega a ^ {\ dagger} a} \ } + {\ frac {1} {Z}} {\ text {Tr}} \ {a ^ {\ dagger} ae ^ {- \ beta \ hbar \ omega a ^ {\ dagger} a} \} = | \ alfa | ^ {2} + {\ frac {1} {Z}} \ sum _ {n = 0} ^ {\ infty} ne ^ {- n \ beta \ hbar \ omega},}

kde za poslední semestr můžeme psát

{\ displaystyle \ sum _ {n = 0} ^ {\ infty} ne ^ {- n \ beta \ hbar \ omega} = - {\ frac {\ částečné} {\ částečné (\ beta \ hbar \ omega)}} \ left (\ sum _ {n = 0} ^ {\ infty} e ^ {- n \ beta \ hbar \ omega} \ right) = {\ frac {e ^ {- \ beta \ hbar \ omega}} {( 1-e ^ {- \ beta \ hbar \ omega}) ^ {2}}}.}

Ve výsledku jsme zjistili

{\ displaystyle \ langle n \ rangle = | \ alpha | ^ {2} + \ langle n \ rangle _ {\ text {th}},}

kde je průměr počtu fotonů vypočítaný s ohledem na tepelný stav. Zde jsme pro snadnost zápisu definovali ${\ displaystyle \ langle n \ rangle _ {\ text {th}}}$

{\ displaystyle \ langle O \ rangle _ {\ text {th}} = {\ frac {1} {Z}} {\ text {tr}} \ {e ^ {- \ beta \ hbar \ omega a ^ {\ dýka} a} O \},}

a píšeme výslovně

{\ displaystyle \ langle n \ rangle _ {\ text {th}} = {\ frac {1} {e ^ {\ beta \ hbar \ omega} -1}}.}

V limitu , který získáme , což odpovídá výrazu pro operátor matice hustoty při nulové teplotě. Podobně lze odchylku počtu fotonů vyhodnotit jako ${\ displaystyle \ beta \ to \ infty}$ ${\ displaystyle \ langle n \ rangle = | \ alpha | ^ {2}}$

{\ displaystyle \ sigma ^ {2} = \ langle n ^ {2} \ rangle - \ langle n \ rangle ^ {2} = \ sigma _ {\ text {th}} ^ {2} + | \ alpha | ^ {2} \ left (1 + 2 \ langle a ^ {\ dagger} a \ rangle _ {\ text {th}} \ right),}

s . Dedukujeme, že druhý moment nelze na rozdíl od průměrné hodnoty (první okamžik) odpojit od tepelných a kvantových distribučních momentů. V tomto smyslu není fotonová statistika posunutého tepelného stavu popsána součtem Poissonových statistik a Boltzmannovy statistiky . Distribuce počátečního tepelného stavu ve fázovém prostoru se rozšiřuje v důsledku koherentního posunutí. ${\ displaystyle \ sigma _ {\ text {th}} ^ {2} = \ langle n ^ {2} \ rangle _ {\ text {th}} - \ langle n \ rangle _ {\ text {th}} ^ {2}}$

Soudržné stavy kondenzátu Bose – Einstein

Bose-Einstein kondenzát (BEC) je kolekce atomů bosonu, které jsou všechny ve stejném kvantovém stavu. V termodynamickém systému se základní stav makroskopicky zabírá pod kritickou teplotou - zhruba, když je tepelná de Broglieho vlnová délka delší než meziatomový odstup. Předpokládá se, že superfluidita v kapalném heliu-4 je spojena s Bose-Einsteinovou kondenzací v ideálním plynu. Ale ⁴ má silné interakce a faktor kapalné struktury (statistika 2. řádu) hraje důležitou roli. Použití koherentního stavu k reprezentaci supratekuté složky ⁴ He poskytlo dobrý odhad frakcí kondenzátu / nekondenzátu v supratekutosti, což odpovídá výsledkům pomalého rozptylu neutronů. Většina speciálních superfluidních vlastností vyplývá přímo z použití koherentního stavu k reprezentaci superfluidní složky - která funguje jako makroskopicky obsazený stav jednoho těla s dobře definovanou amplitudou a fází po celém objemu. (Superfluidní složka ⁴ He přechází z nuly při teplotě přechodu na 100% při absolutní nule. Ale podíl kondenzátu je asi 6% při absolutní nulové teplotě, T = 0K.)
Na začátku studie o superfluiditě navrhli Penrose a Onsager metriku („parametr objednávky“) pro superfluiditu. Představovala ji makroskopická faktorizovaná složka (makroskopická vlastní hodnota) v matici snížené hustoty prvního řádu. Později CN Yang navrhl obecnější měřítko makroskopické kvantové koherence s názvem „Off-Diagonal Long-Range Order“ (ODLRO), které zahrnovalo fermionové i bosonové systémy. ODLRO existuje vždy, když existuje makroskopicky velká faktorizovaná složka (vlastní hodnota) v matici snížené hustoty libovolného řádu. Superfluidita odpovídá velké faktorované složce v matici snížené hustoty prvního řádu. (A všechny matice se sníženou hustotou vyššího řádu se chovají podobně.) Supravodivost zahrnuje velkou faktorovanou součást v matici se sníženou hustotou druhého řádu („ Cooperův elektronový pár “).
Matice se sníženou hustotou používané k popisu makroskopické kvantové koherence v superfluidech jsou formálně stejné jako korelační funkce používané k popisu řádů koherence v záření. Oba jsou příklady makroskopické kvantové koherence. Makroskopicky velká koherentní složka plus šum v elektromagnetickém poli, jak je dáno Glauberovým popisem signálu plus-šum, je formálně stejná jako makroskopicky velká superfluidní složka plus normální tekutá složka v modelu dvou tekutin superfluidity.
Každodenní elektromagnetické záření, jako jsou rádiové a televizní vlny, je také příkladem téměř koherentních stavů (makroskopická kvantová koherence). To by mělo „dát jednu pauzu“, pokud jde o konvenční vymezení mezi kvantovým a klasickým.
Soudržnost v superfluiditě by neměla být přičítána žádné podskupině atomů helia; jedná se o druh kolektivních jevů, do nichž jsou zapojeny všechny atomy (podobně jako u Cooperova párování v supravodivosti, jak je uvedeno v následující části).

Koherentní elektronové stavy v supravodivosti

Elektrony jsou fermiony, ale když se spojí do párů Cooper , chovají se jako bosony, a tak mohou při nízkých teplotách společně vytvářet koherentní stav. Toto párování není ve skutečnosti mezi elektrony, ale ve stavech dostupných elektronům pohybujícím se dovnitř a ven z těchto stavů. Cooperové párování označuje první model supravodivosti.
Tyto koherentní stavy jsou součástí vysvětlení účinků, jako je efekt Quantum Hall v nízkoteplotních supravodivých polovodičích.

Zobecnění

Podle Gilmora a Perelomova, kteří to ukázali samostatně, lze konstrukci koherentních stavů považovat za problém v teorii skupin , a tedy koherentní stavy mohou být spojeny se skupinami odlišnými od Heisenbergovy skupiny , což vede ke kanonickým koherentním stavům diskutovaným výše . Tyto koherentní stavy lze navíc zobecnit na kvantové skupiny . Tato témata s odkazy na původní práci jsou podrobně diskutována v Soudržných stavech v matematické fyzice .

V kvantové teorii pole a teorii strun je zobecnění koherentních stavů pro případ, kdy se k definování vakuového stavu s jinou hodnotou očekávaného vakua než původní vakuum používá nekonečně mnoho stupňů volnosti .
V jednorozměrných mnohočetných kvantových systémech s fermionickými stupni volnosti lze nízkoenergetické excitované stavy aproximovat jako koherentní stavy operátora bosonického pole, které vytváří buzení částic. Tento přístup se nazývá bosonizace .
Gaussovské koherentní stavy nerelativistické kvantové mechaniky lze zobecnit na relativistické koherentní stavy Klein-Gordonových a Diracových částic.
Koherentní stavy se objevily také v pracích o smyčkové kvantové gravitaci nebo o konstrukci (polo) klasické kanonické kvantové obecné relativity.

Languages

In other projects

Soudržný stav - Coherent state

Obsah