Rovnice spojitosti - Continuity equation

Rovnice kontinuity nebo doprava rovnice je rovnice , která popisuje přepravu některých množství. Je obzvláště jednoduchý a účinný, když je aplikován na konzervované množství , ale lze jej zobecnit, aby se aplikoval na jakékoli rozsáhlé množství . Vzhledem k tomu, že hmotnost , energie , hybnost , elektrický náboj a další přírodní veličiny jsou zachovány za příslušných příslušných podmínek, lze pomocí rovnic spojitosti popsat různé fyzikální jevy.

Rovnice kontinuity jsou silnější, místní formou zákonů zachování . Například slabá verze zákona zachování energetických stavů uvádí, že energii nelze ani vytvořit, ani zničit - tj. Celkové množství energie ve vesmíru je pevně dané. Toto tvrzení nevylučuje možnost, že by množství energie mohlo zmizet z jednoho bodu a současně se objevit v jiném bodě. Silnější tvrzení je, že energie je lokálně konzervována: energii nelze ani vytvářet, ani ničit, ani ji nelze „ teleportovat “ z jednoho místa na druhé - může se pohybovat pouze nepřetržitým tokem. Rovnice kontinuity je matematický způsob vyjádření tohoto druhu prohlášení. Například rovnice kontinuity pro elektrický náboj uvádí, že množství elektrického náboje v jakémkoli objemu prostoru se může měnit pouze podle množství elektrického proudu protékajícího do nebo z tohoto objemu přes jeho hranice.

Rovnice spojitosti mohou obecně zahrnovat termíny „zdroj“ a „potopení“, které jim umožňují popsat množství, která jsou často, ale ne vždy konzervována, jako je hustota molekulárních druhů, které mohou být vytvořeny nebo zničeny chemickými reakcemi. V každodenním příkladu existuje rovnice kontinuity pro počet živých lidí; má „zdrojový termín“, který odpovídá narozeným lidem, a „potopný termín“, který odpovídá lidem, kteří umírají.

Jakákoli rovnice kontinuity může být vyjádřena v „integrální formě“ (ve smyslu integrálu toku ), která platí pro jakoukoli konečnou oblast, nebo v „diferenciální formě“ (pokud jde o divergenční operátor), která platí v bodě.

Rovnice spojitosti jsou základem konkrétnějších transportních rovnic, jako je konvekční – difúzní rovnice , Boltzmannova dopravní rovnice a Navier – Stokesovy rovnice .

Toky řízené rovnicemi kontinuity lze zobrazit pomocí Sankeyova diagramu .

Obecná rovnice

Definice toku

Rovnice kontinuity je užitečná, když lze definovat tok . K definování toku musí nejprve existovat množství $q,$ které může proudit nebo se pohybovat, jako je hmotnost , energie , elektrický náboj , hybnost , počet molekul atd. Nechť $ρ$ je objemová hustota této veličiny, tj. Množství $q$ na jednotku objemu.

Způsob, jakým toto množství $q$ proudí, je popsán jeho tokem . Tok $q$ je vektorové pole , které označíme jako j . Zde je několik příkladů a vlastností tavidla:

Dimenze toku je „množství $q$ proudícího za jednotku času, přes jednotkovou oblast“. Například v rovnici hmotnostní kontinuity pro tekoucí vodu platí, že pokud trubkou o průřezu 1 cm ² protéká 1 gram vody za sekundu , pak průměrný hmotnostní tok $j$ uvnitř potrubí je (1 g /s) / cm ² , a jeho směr je podél potrubí ve směru, kterým voda proudí. Mimo potrubí, kde není voda, je tok nulový.
Pokud existuje rychlostní pole $u,$ které popisuje příslušný tok - jinými slovy, pokud se veškerá veličina $q$ v bodě $x$ pohybuje rychlostí $u (x)$ -, pak je tok podle definice roven hustotě a krát rychlostnímu poli : ${\ Displaystyle \ mathbf {j} = \ rho \ mathbf {u}}$ Například pokud v rovnici hmotnostní kontinuity pro tekoucí vodu $u$ je rychlost vody v každém bodě a $ρ$ je hustota vody v každém bodě, pak $j$ by byl hmotnostní tok.
V dobře známém například tok elektrického náboje je elektrický proud hustota .

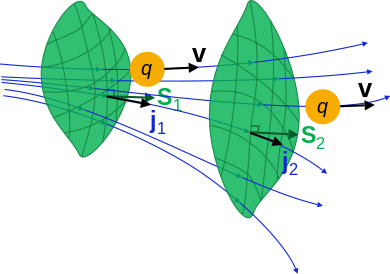Ilustrace jak tok $j$ z množství $q$ prochází otevřeným povrchem $S$ . ( $d S$ je diferenciální vektorová oblast ).
Pokud existuje imaginární povrch $S$ , pak je povrchový integrál toku přes $S$ roven množství $q,$ které prochází povrchem $S$ za jednotku času:

${\ Displaystyle ({\ text {Ohodnoťte to}} q {\ text {teče pomyslnou plochou}} S) = \ iint _ {S} \ mathbf {j} \ cdot d \ mathbf {S}}$

ve kterém je povrchový integrál . ${\ textstyle \ iint _ {S} d \ mathbf {S}}$

(Všimněte si, že koncept, který je zde nazýván „tok“, je v některé literatuře alternativně nazýván „hustota toku“, v jehož kontextu „tok“ označuje povrchový integrál hustoty toku. Podrobnosti viz hlavní článek o toku .)

Integrální forma

Integrální forma rovnice kontinuity uvádí, že:

Množství $q$ v oblasti se zvyšuje, když další $q$ proudí dovnitř povrchem oblasti, a klesá, když proudí ven;
Množství $q$ v oblasti se zvyšuje, když je uvnitř $q$ vytvořeno nové $q$ , a klesá, když je $q$ zničeno;
Kromě těchto dvou procesů neexistuje žádný jiný způsob, jak se množství $q$ v oblasti změnit.

Matematicky je integrální forma rovnice kontinuity vyjadřující rychlost nárůstu $q$ v objemu $V$ :

${\ displaystyle {\ frac {dq} {dt}}+}$ $\ oiint$ ${\ displaystyle \ scriptstyle S}$ ${\ Displaystyle \ mathbf {j} \ cdot d \ mathbf {S} = \ Sigma}$

V integrální formě rovnice kontinuity je

S

jakýkoli uzavřený povrch, který zcela uzavírá objem

V

, jako kterýkoli z povrchů vlevo.

S

může to být povrch s hranicemi, stejně jako na pravé straně. (Povrchy jsou modré, hranice jsou červené.)

kde

$S$ je jakýkoli imaginární uzavřený povrch , který obklopuje svazek $V$ ,
$\ oiint$ $S$ $d S$ označujepovrchový integrálnad tímto uzavřeným povrchem,
$q$ je celkové množství množství v objemu $V$ ,
$j$ je tok $q$ ,
$t$ je čas,
$Σ$ je čistá sazba, kterou $q$ generuje uvnitř objemu $V$ za jednotku času. Když $q$ je generován, se nazývá zdroj o $q$ , a to je $Σ$ více pozitivní. Když $q$ je zničena, se nazývá jímky o $q$ , a to je $å$ negativnější. Tento termín je někdy psán jako nebo celková změna q z jeho generování nebo zničení uvnitř řídicího svazku. ${\ displaystyle dq/dt | _ {\ text {gen}}}$

V jednoduchém příkladu $V$ může být budova a $q$ může být počet lidí v budově. Povrch $S$ bude sestávat ze stěn, dveří, střechy a základu budovy. Potom rovnice kontinuity uvádí, že počet lidí v budově se zvyšuje, když lidé vstupují do budovy (vnitřní tok povrchem), klesá, když lidé opouštějí budovu (vnější tok povrchem), zvyšuje se, když někdo v budově dává narození (zdroj, $Σ> 0$ ), a klesá, když někdo v budově zemře (umyvadlo, $Σ <0$ ).

Diferenciální forma

Podle divergenční věty lze obecnou rovnici spojitosti zapsat také v „diferenciální formě“:

${\ Displaystyle {\ frac {\ částečné \ rho} {\ částečné t}}+\ nabla \ cdot \ mathbf {j} = \ sigma}$

kde

$Div$ je divergence ,
$ρ$ je množství množství $q$ na jednotku objemu,
$j$ je tok $q$ ,
$t$ je čas,
$σ$ je generování $q$ na jednotku objemu za jednotku času. Termíny, které generují $q$ (tj. $Σ > 0$ ) nebo odebírají $q$ (tj. $Σ <0$ ), se označují jako „zdroje“ a „propady“.

Tuto obecnou rovnici lze použít k odvození jakékoli rovnice kontinuity, sahající od jednoduché rovnice pro objemovou kontinuitu po stejně komplikovanou jako Navier -Stokesovy rovnice . Tato rovnice také zobecňuje rovnici advekce . Jiné fyzikální rovnice, jako je Gaussův zákon elektrického pole a Gaussův zákon pro gravitaci , mají podobnou matematickou formu jako rovnice kontinuity, ale nejsou obvykle označovány termínem „rovnice kontinuity“, protože $j$ v těchto případech neplatí představují tok skutečné fyzické veličiny.

V případě, že $q$ je zachovaná veličina, kterou nelze vytvořit ani zničit (například energii ), $σ = 0$ a rovnice se stanou:

{\ Displaystyle {\ frac {\ částečné \ rho} {\ částečné t}}+\ nabla \ cdot \ mathbf {j} = 0}

Elektromagnetismus

V elektromagnetické teorii je rovnice kontinuity empirický zákon vyjadřující (místní) zachování náboje . Matematicky je to automatický důsledek Maxwellových rovnic , ačkoli zachování náboje je zásadnější než Maxwellovy rovnice. Uvádí, že rozdíly v proudové hustoty $J$ (v ampérech na čtvereční metr), je rovna záporné rychlosti změny hustoty náboje $p$ (v coulombs na metr krychlový),

{\ Displaystyle \ nabla \ cdot \ mathbf {J} =-{\ frac {\ částečné \ rho} {\ částečné t}}}

Soulad s Maxwellovými rovnicemi

Uvádí to jedna z Maxwellových rovnic , Ampèrův zákon (s Maxwellovou korekcí)

{\ Displaystyle \ nabla \ times \ mathbf {H} = \ mathbf {J} +{\ frac {\ partial \ mathbf {D}} {\ partial t}}.}

Vezmeme -li divergenci obou stran (divergence a parciální derivace v čase dojíždění), výsledkem je

{\ Displaystyle \ nabla \ cdot (\ nabla \ times \ mathbf {H}) = \ nabla \ cdot \ mathbf {J} +{\ frac {\ částečná (\ nabla \ cdot \ mathbf {D})} {\ částečná t}},}

ale divergence zvlnění je nulová, takže

{\ Displaystyle \ nabla \ cdot \ mathbf {J} +{\ frac {\ částečná (\ nabla \ cdot \ mathbf {D})} {\ částečná t}} = 0.}

To ale uvádí Gaussův zákon (další Maxwellova rovnice)

{\ Displaystyle \ nabla \ cdot \ mathbf {D} = \ rho,}

které lze nahradit v předchozí rovnici za vzniku rovnice kontinuity

{\ Displaystyle \ nabla \ cdot \ mathbf {J} +{\ frac {\ částečné \ rho} {\ částečné t}} = 0.}

Aktuální je pohyb náboje. Rovnice kontinuity říká, že pokud se náboj pohybuje z diferenciálního objemu (tj. Divergence proudové hustoty je kladná), pak se množství náboje v tomto objemu sníží, takže rychlost změny hustoty náboje je záporná. Rovnice kontinuity tedy znamená zachování náboje.

Pokud existují magnetické monopoly , existovala by rovnice kontinuity i pro monopólové proudy, viz článek monopolu o pozadí a dualitě mezi elektrickými a magnetickými proudy.

Dynamika tekutin

V dynamice tekutin rovnice kontinuity uvádí, že rychlost, kterou hmota vstupuje do systému, se rovná rychlosti, kterou hmota opouští systém, plus akumulace hmoty v systému. Diferenciální forma rovnice kontinuity je:

{\ Displaystyle {\ frac {\ částečné \ rho} {\ částečné t}}+\ nabla \ cdot (\ rho \ mathbf {u}) = 0}

kde

$ρ$ je hustota kapaliny,
$t$ je čas,
$u$ je vektorové pole rychlosti proudění .

Časovou derivaci lze chápat jako akumulaci (nebo ztrátu) hmoty v systému, zatímco divergenční člen představuje rozdíl v toku v porovnání s odtokem. V této souvislosti je tato rovnice také jednou z Eulerových rovnic (dynamika tekutin) . Tyto Navier-Stokesovy rovnice tvoří vektor rovnice kontinuity popisující zachování hybnosti .

Pokud je tekutina nestlačitelná (objemová deformační rychlost je nulová), rovnice kontinuity hmotnosti se zjednoduší na rovnici kontinuity objemu:

{\ Displaystyle \ nabla \ cdot \ mathbf {u} = 0,}

což znamená, že divergence rychlostního pole je všude nulová. Fyzicky se to rovná tvrzení, že rychlost místního objemového dilatace je nulová, a proto se tok vody sbíhajícím potrubím upraví pouze zvýšením jeho rychlosti, protože voda je z velké části nestlačitelná.

Počítačové vidění

V počítačovém vidění je optický tok vzorem zdánlivého pohybu předmětů ve vizuální scéně. Za předpokladu, že se jas pohybujícího se objektu mezi dvěma obrazovými snímky nezměnil, lze rovnici optického toku odvodit jako:

{\ Displaystyle {\ frac {\ částečný I} {\ částečný x}} V_ {x}+{\ frac {\ částečný I} {\ částečný y}} V_ {y}+{\ frac {\ částečný I} { \ částečné t}} = \ nabla I \ cdot \ mathbf {V} +{\ frac {\ částečné I} {\ částečné t}} = 0}

kde

$t$ je čas,
souřadnice $x$ $,$ $y$ na obrázku,
$I$ je intenzita obrazu v souřadnicích obrazu ( x , y ) a čase t ,
$V$ je vektor optické rychlosti prouděnív souřadnicích obrazu ( x , y ) a čase t ${\ displaystyle (V_ {x}, V_ {y})}$

Energie a teplo

Zachování energie říká, že energii nelze vytvářet ani ničit. ( Nuance spojené s obecnou relativitou viz níže .) Proto pro tok energie existuje rovnice kontinuity:

{\ Displaystyle {\ frac {\ částečné u} {\ částečné t}}+\ nabla \ cdot \ mathbf {q} = 0}

kde

$u$ , místní hustota energie (energie na jednotku objemu),
$q$ , tok energie (přenos energie na jednotku plochy průřezu za jednotku času) jako vektor,

Důležitým praktickým příkladem je tok tepla . Když teplo proudí uvnitř tělesa, rovnici spojitosti lze zkombinovat s Fourierovým zákonem (tepelný tok je úměrný teplotnímu gradientu), aby se dospělo k tepelné rovnici . Rovnice toku tepla může mít také zdrojové termíny: Přestože energii nelze vytvářet ani ničit, teplo lze vytvářet z jiných druhů energie, například třením nebo joulovým ohřevem .

Rozdělení pravděpodobnosti

Pokud existuje množství, které se pohybuje kontinuálně podle stochastického (náhodného) procesu, jako je umístění jediné rozpuštěné molekuly s Brownovým pohybem , pak existuje rovnice kontinuity pro její rozdělení pravděpodobnosti . Tok v tomto případě je pravděpodobnost na jednotku plochy za jednotku času, kdy částice prochází povrchem. Podle rovnice kontinuity se záporná divergence tohoto toku rovná rychlosti změny hustoty pravděpodobnosti . Rovnice kontinuity odráží skutečnost, že molekula je vždy někde - integrál jejího rozdělení pravděpodobnosti je vždy roven 1 - a že se pohybuje spojitým pohybem (bez teleportace ).

Kvantová mechanika

Kvantová mechanika je další doménou, kde existuje rovnice kontinuity související se zachováním pravděpodobnosti . Termíny v rovnici vyžadují následující definice a jsou o něco méně zřejmé než ostatní výše uvedené příklady, takže jsou zde nastíněny:

Wavefunction $Ψ$ pro jednu částici v polohovém prostoru (spíše než prostor hybností ), to znamená, je funkcí polohy $r$ a času $t$ , $ln = ln (r, t)$ .
Funkce hustoty pravděpodobnosti je ${\ Displaystyle \ rho (\ mathbf {r}, t) = \ Psi ^{*} (\ mathbf {r}, t) \ Psi (\ mathbf {r}, t) = | \ Psi (\ mathbf {r }, t) |^{2}.}$
Pravděpodobnost nalezení částice ve $V$ v $t$ je označena a definována ${\ Displaystyle P = P _ {\ mathbf {r} \ in V} (t) = \ int _ {V} \ Psi ^{*} \ Psi dV = \ int _ {V} | \ Psi | ^{2} dV.}$
Proud pravděpodobnosti (aka pravděpodobnosti toku) je ${\ Displaystyle \ mathbf {j} (\ mathbf {r}, t) = {\ frac {\ hbar} {2mi}} \ left [\ Psi ^{*} \ left (\ nabla \ Psi \ right)-\ Psi \ left (\ nabla \ Psi ^{*} \ right) \ right].}$

S těmito definicemi rovnice kontinuity zní:

{\ Displaystyle \ nabla \ cdot \ mathbf {j} +{\ frac {\ částečné \ rho} {\ částečné t}} = 0 \ mathrel {\ rightleftharpoons} \ nabla \ cdot \ mathbf {j} +{\ frac { \ částečné | \ Psi |^{2}} {\ částečné t}} = 0.}

Může být uvedena jakákoli forma. Výše uvedené veličiny intuitivně naznačují, že to představuje tok pravděpodobnosti. Pravděpodobnost nalezení částice na některé pozice $r$ a čas $t$ toků se jako tekutina ; odtud termín pravděpodobnostní proud , vektorové pole . Částice sám o sobě není průtok deterministicky v této vektorového pole .

Soulad se Schrödingerovou rovnicí

3-d časově závislá Schrödingerova rovnice a její komplexní konjugát ( $i \to -i$ v celém textu) jsou:

{\ displaystyle {\ begin {aligned}-{\ frac {\ hbar ^{2}} {2m}} \ nabla ^{2} \ Psi +U \ Psi & = i \ hbar {\ frac {\ partial \ Psi } {\ partial t}}, \\-{\ frac {\ hbar ^{2}} {2m}} \ nabla ^{2} \ Psi ^{*}+U \ Psi ^{*} & =-i \ hbar {\ frac {\ částečné \ Psi ^{*}} {\ částečné t}}, \\\ konec {zarovnáno}}}

kde

U

je potenciální funkce . Parciální derivace z

p

vzhledem k

t

je:

{\ Displaystyle {\ frac {\ částečné \ rho} {\ částečné t}} = {\ frac {\ částečné | \ Psi |^{2}} {\ částečné t}} = {\ frac {\ částečné} {\ částečné t}} \ vlevo (\ Psi ^{*} \ Psi \ vpravo) = \ Psi ^{*} {\ frac {\ částečné \ Psi} {\ částečné t}}+\ Psi {\ frac {\ částečné \ Psi ^{*}} {\ částečné t}}.}

Násobení Schrödingerovy rovnice $Ψ*$ a řešení pro $Ψ*.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} ∂Ψ/∂ t$ a podobně vynásobením komplexní konjugované Schrödingerovy rovnice $Ψ$ pak řešením pro $Ψ \partialΨ* / \partial t$ ;

{\ Displaystyle {\ begin {aligned} \ Psi ^{*} {\ frac {\ částečné \ Psi} {\ částečné t}} & = {\ frac {1} {i \ hbar}} \ left [-{\ frac {\ hbar ^{2} \ Psi ^{*}} {2m}} \ nabla ^{2} \ Psi +U \ Psi ^{*} \ Psi \ right], \\\ Psi {\ frac {\ částečné \ Psi ^{*}} {\ částečné t}} & =-{\ frac {1} {i \ hbar}} \ left [-{\ frac {\ hbar ^{2} \ Psi} {2m}} \ nabla ^{2} \ Psi ^{*}+U \ Psi \ Psi ^{*} \ right], \\\ end {aligned}}}

dosazení do časové derivace $ρ$ :

{\ Displaystyle {\ begin {aligned} {\ frac {\ částečné \ rho} {\ částečné t}} & = {\ frac {1} {i \ hbar}} \ left [-{\ frac {\ hbar ^{ 2} \ Psi ^{*}} {2m}} \ nabla ^{2} \ Psi +U \ Psi ^{*} \ Psi \ right]-{\ frac {1} {i \ hbar}} \ left [ -{\ frac {\ hbar ^{2} \ Psi} {2m}} \ nabla ^{2} \ Psi ^{*}+U \ Psi \ Psi ^{*} \ right] \\ & = {\ frac {1} {i \ hbar}} \ left [-{\ frac {\ hbar ^{2} \ Psi ^{*}} {2m}} \ nabla ^{2} \ Psi +U \ Psi ^{*} \ Psi \ right]+{\ frac {1} {i \ hbar}} \ left [+{\ frac {\ hbar ^{2} \ Psi} {2m}} \ nabla ^{2} \ Psi ^{* } -U \ Psi ^{*} \ Psi \ right] \\ [2pt] & =-{\ frac {1} {i \ hbar}} {\ frac {\ hbar ^{2} \ Psi ^{*} } {2m}} \ nabla ^{2} \ Psi +{\ frac {1} {i \ hbar}} {\ frac {\ hbar ^{2} \ Psi} {2m}} \ nabla ^{2} \ Psi ^{*} \\ [2pt] & = {\ frac {\ hbar} {2im}} \ left [\ Psi \ nabla ^{2} \ Psi ^{*}-\ Psi ^{*} \ nabla ^ {2} \ Psi \ right] \\\ end {zarovnaný}}}

Tyto Laplacian operátory ( $\nabla 2$ ) ve výše uvedené výsledku ukazují, že na pravé straně je divergence $j$ , a v obráceném pořadí termínů vyplývá, to je negativní $j$ , celkem:

{\ Displaystyle {\ begin {aligned} \ nabla \ cdot \ mathbf {j} & = \ nabla \ cdot \ left [{\ frac {\ hbar} {2mi}} \ left (\ Psi ^{*} \ left ( \ nabla \ Psi \ right)-\ Psi \ left (\ nabla \ Psi ^{*} \ right) \ right) \ right] \\ & = {\ frac {\ hbar} {2mi}} \ left [\ Psi ^{*} \ left (\ nabla ^{2} \ Psi \ right)-\ Psi \ left (\ nabla ^{2} \ Psi ^{*} \ right) \ right] \\ & =-{\ frac {\ hbar} {2mi}} \ left [\ Psi \ left (\ nabla ^{2} \ Psi ^{*} \ right)-\ Psi ^{*} \ left (\ nabla ^{2} \ Psi \ vpravo) \ vpravo] \\\ konec {zarovnaný}}}

rovnice spojitosti je tedy:

{\ Displaystyle {\ begin {aligned} & {\ frac {\ částečné \ rho} {\ částečné t}} =-\ nabla \ cdot \ mathbf {j} \\ [3pt] {} \ Rightarrow {} & {\ frac {\ částečné \ rho} {\ částečné t}}+\ nabla \ cdot \ mathbf {j} = 0 \\\ end {zarovnáno}}}

Integrální forma následuje jako pro obecnou rovnici.

Polovodič

Celkový tok proudu v polovodiči se skládá z driftového proudu a difuzního proudu jak elektronů ve vodivém pásmu, tak otvorů ve valenčním pásmu.

Obecný formulář pro elektrony v jedné dimenzi:

{\ Displaystyle {\ frac {\ částečný n} {\ částečný t}} = n \ mu _ {n} {\ frac {\ částečný E} {\ částečný x}}+\ mu _ {n} E {\ frac {\ částečné n} {\ částečné x}}+D_ {n} {\ frac {\ částečné ^{2} n} {\ částečné x ^{2}}}+(G_ {n} -R_ {n}) }

kde:

n je místní koncentrace elektronů
${\ displaystyle \ mu _ {n}}$ je pohyblivost elektronů
E je elektrické pole v oblasti vyčerpání
D _n je difúzní koeficient pro elektrony
G _n je rychlost generování elektronů
R _n je rychlost rekombinace elektronů

Podobně pro otvory:

{\ Displaystyle {\ frac {\ částečný p} {\ částečný t}} =-p \ mu _ {p} {\ frac {\ částečný E} {\ částečný x}}-\ mu _ {p} E {\ frac {\ částečný p} {\ částečný x}}+D_ {p} {\ frac {\ částečný ^{2} p} {\ částečný x ^{2}}}+(G_ {p} -R_ {p} )}

kde:

p je místní koncentrace otvorů
${\ displaystyle \ mu _ {p}}$ je pohyblivost děr
E je elektrické pole v oblasti vyčerpání
D _p je difúzní koeficient pro otvory
G _p je rychlost generování děr
R _p je rychlost rekombinace děr

Derivace

Tato část uvádí odvození výše uvedené rovnice pro elektrony. Podobnou derivaci lze nalézt pro rovnici pro otvory.

Vezměte v úvahu skutečnost, že počet elektronů je zachován v celém objemu polovodičového materiálu s plochou průřezu, A a délkou, dx , podél osy x . Přesněji lze říci:

{\ Displaystyle {\ text {Míra změny hustoty elektronů}} = ({\ text {Electron flux in}}-{\ text {Electron flux out}})+{\ text {Net generation inside a volume}}}

Matematicky lze tuto rovnost zapsat:

{\ displaystyle {\ begin {aligned} {\ frac {dn} {dt}} A \, dx & = [J (x+dx) -J (x)] {\ frac {A} {e}}+(G_ {n} -R_ {n}) A \, dx \\ [3pt] {\ frac {dn} {dt}} A \, dx & = [J (x)+{\ frac {dJ} {dx}} dx -J (x)] {\ frac {A} {e}}+(G_ {n} -R_ {n}) A \, dx \\ [3pt] {\ frac {dn} {dt}} & = { \ frac {1} {e}} {\ frac {dJ} {dx}}+(G_ {n} -R_ {n}) \ end {zarovnáno}}}

Zde J označuje proudovou hustotu (jejíž směr je konvenčně proti toku elektronů) v důsledku toku elektronů v uvažovaném objemu polovodiče. Říká se mu také hustota elektronového proudu.

Celková hustota proudu elektronu je součtem hustot driftového proudu a difuzního proudu:

{\ Displaystyle J_ {n} = en \ mu _ {n} E+eD_ {n} {\ frac {dn} {dx}}}

Proto máme

{\ Displaystyle {\ frac {dn} {dt}} = {\ frac {1} {e}} {\ frac {d} {dx}} \ left (en \ mu _ {n} E+eD_ {n} {\ frac {dn} {dx}} \ right)+(G_ {n} -R_ {n})}

Výsledkem použití pravidla produktu je konečný výraz:

{\ Displaystyle {\ frac {dn} {dt}} = \ mu _ {n} E {\ frac {dn} {dx}}+\ mu _ {n} n {\ frac {dE} {dx}}+ D_ {n} {\ frac {d^{2} n} {dx^{2}}}+(G_ {n} -R_ {n})}

Řešení

Klíčem k řešení těchto rovnic v reálných zařízeních je, kdykoli je to možné, vybrat oblasti, ve kterých je většina mechanismů zanedbatelná, aby se rovnice zmenšily na mnohem jednodušší formu.

Relativistická verze

Speciální relativita

Zápis a nástroje speciální relativity , zejména 4-vektory a 4-gradienty , nabízejí pohodlný způsob zápisu jakékoli rovnice spojitosti.

Hustotu veličiny $ρ$ a její proud $j$ lze zkombinovat do 4 vektoru nazývaného 4 proud :

{\ Displaystyle J = \ left (c \ rho, j_ {x}, j_ {y}, j_ {z} \ right)}

kde

c

je rychlost světla . 4- Divergence tohoto proudu je:

{\ Displaystyle \ partial _ {\ mu} J^{\ mu} = c {\ frac {\ částečné \ rho} {\ částečné ct}}+\ nabla \ cdot \ mathbf {j}}

kde

\partial μ

je 4-gradient a

μ

je index označující rozměr časoprostoru . Rovnice spojitosti pak je:

{\ Displaystyle \ partial _ {\ mu} J^{\ mu} = 0}

v obvyklém případě, kdy neexistují žádné zdroje nebo jímky, tj. pro dokonale konzervovaná množství, jako je energie nebo náboj. Tato rovnice kontinuity je zjevně („zjevně“) Lorentzově invariantní .

Příklady rovnic kontinuity často psaných v této formě zahrnují zachování elektrického náboje

{\ Displaystyle \ partial _ {\ mu} J^{\ mu} = 0}

kde

J

je elektrický 4-proud ; a zachování hybnosti energie

{\ Displaystyle \ partial _ {\ nu} T^{\ mu \ nu} = 0}

kde

T

je tenzor napětí – energie .

Obecná relativita

V obecné relativitě , kde je časoprostor zakřivený, rovnice kontinuity (v diferenciální formě) pro energii, náboj nebo jiné konzervované veličiny zahrnuje kovarianční divergenci místo běžné divergence.

Například tenzor napětí – energie je tenzorové pole druhého řádu obsahující hustoty energie – hybnosti, toky energie – hybnosti a smyková napětí o distribuci hmotné energie. Diferenciální forma zachování energie a hybnosti v obecné relativitě uvádí, že kovarianční divergence tenzoru napětí-energie je nulová:

{\ Displaystyle {T^{\ mu}} _ {\ nu; \ mu} = 0.}

Toto je důležité omezení formy, kterou mají Einsteinovy rovnice pole v obecné relativitě .

Avšak běžné divergence na stres-energie tensor však není nutně zmizí:

{\ Displaystyle \ partial _ {\ mu} T^{\ mu \ nu} =-\ Gamma _ {\ mu \ lambda}^{\ mu} T^{\ lambda \ nu}-\ Gamma _ {\ mu \ lambda}^{\ nu} T^{\ mu \ lambda},}

Pravá strana striktně zmizí pouze pro plochou geometrii.

V důsledku toho je integrální forma rovnice kontinuity obtížně definovatelná a nemusí nutně platit pro oblast, v níž je časoprostor výrazně zakřivený (např. Kolem černé díry nebo napříč celým vesmírem).

Fyzika částic

Kvarky a gluony mají barevný náboj , který je vždy zachován jako elektrický náboj, a pro takové proudy barevného náboje existuje rovnice kontinuity (explicitní výrazy pro proudy jsou uvedeny v tenzoru síly pole gluonu ).

Ve fyzice částic existuje mnoho dalších veličin, které jsou často nebo vždy konzervovány: baryonové číslo (úměrné počtu kvarků minus počet antikvarků), elektronové číslo, mu číslo, tau číslo , isospin a další. Každý z nich má odpovídající rovnici kontinuity, případně včetně podmínek zdroje / jímky.

Noetherova věta

Jedním z důvodů, proč se ve fyzice často vyskytují rovnice zachování, je Noetherova věta . Toto uvádí, že kdykoli mají fyzikální zákony spojitou symetrii , existuje rovnice kontinuity pro nějakou zachovanou fyzikální veličinu. Tři nejznámější příklady jsou:

Fyzikální zákony jsou neměnné, pokud jde o časový překlad- například fyzikální zákony jsou dnes stejné jako včera. Tato symetrie vede k rovnici kontinuity pro zachování energie .
Fyzikální zákony jsou neměnné, pokud jde o vesmírný překlad-například fyzikální zákony v Brazílii jsou stejné jako fyzikální zákony v Argentině. Tato symetrie vede k rovnici kontinuity pro zachování hybnosti .
Fyzikální zákony jsou vzhledem k orientaci invariantní - například když se vznáší ve vesmíru, neexistuje žádné měření, které byste mohli říci, „která cesta je nahoru“; fyzikální zákony jsou stejné bez ohledu na to, jak jste orientovaní. Tato symetrie vede k rovnici kontinuity pro zachování momentu hybnosti .

Viz také

Reference

Další čtení

Hydrodynamika, H. Lamb , Cambridge University Press, (2006 digitalizace 6. vydání 1932) ISBN 978-0-521-45868-9
Úvod do elektrodynamiky (3. vydání), DJ Griffiths , Pearson Education Inc, 1999, ISBN 81-7758-293-3
Elektromagnetismus (2. vydání), IS Grant, WR Phillips , Manchester Physics Series, 2008 ISBN 0-471-92712-0
Gravitace, JA Wheeler, C. Misner, KS Thorne , WH Freeman & Co, 1973, ISBN 0-7167-0344-0

Languages

In other projects