Konvoluce - Convolution

Vizuální srovnání konvoluce, křížové korelace a autokorelace . Pro operace zahrnující funkci f a za předpokladu, že výška f je 1,0, je hodnota výsledku v 5 různých bodech označena stínovanou oblastí pod každým bodem. Důvodem je také symetrie f a v tomto příkladu jsou totožné.${\ displaystyle g*f}$${\ displaystyle f \ star g}$

V matematiky (zejména funkční analýzy ), konvoluce je matematická operace na dvou funkcí ( f a g ), který vytváří třetí funkci ( ), který vyjadřuje, jak se tvar jedné modifikované jiný. Termín konvoluce se týká jak výsledkové funkce, tak procesu jejího výpočtu. Je definován jako integrál součinu dvou funkcí poté, co je jedna obrácena a posunuta. Integrál je vyhodnocen pro všechny hodnoty posunu, čímž vzniká konvoluční funkce. ${\ displaystyle f*g}$

Některé vlastnosti konvoluce jsou podobné křížové korelaci : u funkcí s reálnou hodnotou se spojitá nebo diskrétní proměnná liší od křížové korelace ( ) pouze v tom, že buď f ( x ) nebo g ( x ) se odráží na y -osa; jde tedy o vzájemnou korelaci f ( x ) a g ( -x ) nebo f ( -x ) a g ( x ) . U složitějších-cenil funkce, operátor cross-korelace je adjoint provozovatele konvoluce. ${\ displaystyle f \ star g}$

Konvoluce má aplikace, které zahrnují pravděpodobnost , statistiky , akustiku , spektroskopii , zpracování signálu a zpracování obrazu , inženýrství , fyziku , počítačové vidění a diferenciální rovnice .

Konvoluci lze definovat pro funkce v euklidovském prostoru a dalších skupinách . Například periodické funkce , jako je Fourierova transformace s diskrétním časem , lze definovat na kružnici a konvolvovat periodickou konvolucí . (Viz řádek 18 v DTFT § Vlastnosti .) Pro funkce na sadě celých čísel lze definovat diskrétní konvoluci .

Zobecnění konvoluce má aplikace v oblasti numerické analýzy a numerické lineární algebry a v návrhu a implementaci filtrů konečné odezvy impulzů při zpracování signálu.

Výpočet inverzní operace konvoluce je známý jako dekonvoluce .

Definice

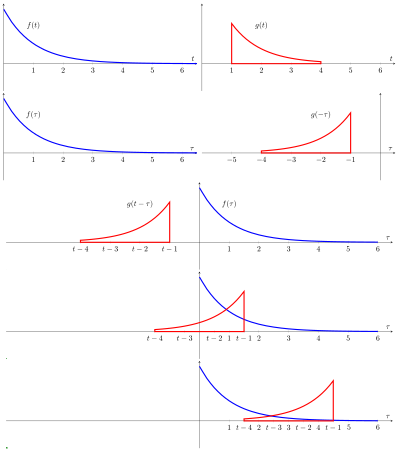
Konvoluce f a g je napsána f ∗ g , označující operátor symbolem ∗ . Je definován jako integrál součinu dvou funkcí poté, co je jedna obrácena a posunuta. Jedná se tedy o zvláštní druh integrální transformace :

${\ Displaystyle (f*g) (t): = \ int _ {-\ infty}^{\ infty} f (\ tau) g (t- \ tau) \, d \ tau.}$

Ekvivalentní definice je (viz komutativita ):

${\ Displaystyle (f*g) (t): = \ int _ {-\ infty}^{\ infty} f (t- \ tau) g (\ tau) \, d \ tau.}$

Zatímco symbol t je použit výše, nemusí představovat časovou doménu. Ale v tomto kontextu lze konvoluční vzorec popsat jako oblast pod funkcí f ( τ ) váženou funkcí g ( - τ ) posunutou o množství t . Jako t se mění, vážící funkce g ( t - τ ) zdůrazňuje různé části vstupní funkce f ( ▼ se ) .

U funkcí f , g podporovaných pouze na [0, ∞) (tj. Nula pro negativní argumenty) lze integrační limity zkrátit, což má za následek:

${\ Displaystyle (f*g) (t) = \ int _ {0}^{t} f (\ tau) g (t- \ tau) \, d \ tau \ quad \ {\ text {for}} f , g: [0, \ infty) \ to \ mathbb {R}.}$

Pro vícedimenzionální formulaci konvoluce viz definiční doména (níže).

Zápis

Běžnou technickou notační konvencí je:

${\ Displaystyle f (t)*g (t) \ mathrel {: =} \ underbrace {\ int _ {-\ infty}^{\ infty} f (\ tau) g (t- \ tau) \, d \ tau} _ {(f*g) (t)},}$

což je třeba interpretovat opatrně, aby nedošlo k záměně. Například f ( t ) ∗ g ( t - t ₀ ) je ekvivalentní ( f ∗ g ) ( t - t ₀ ) , ale f ( t - t ₀ ) ∗ g ( t - t ₀ ) je ve skutečnosti ekvivalentní do ( f ∗ g ) ( t - 2 t ₀ ) .

Odvození

Konvoluce popisuje výstup (pokud jde o vstup) důležité třídy operací známých jako lineární časově invariantní (LTI). Viz teorie systému LTI o odvození konvoluce v důsledku omezení LTI. Pokud jde o Fourierovy transformace vstupu a výstupu operace LTI, nevytvářejí se žádné nové frekvenční složky. Stávající jsou pouze upraveny (amplituda a/nebo fáze). Jinými slovy, výstupní transformace je bodovým součinem vstupní transformace se třetí transformací (známá jako přenosová funkce ). Odvození této vlastnosti konvoluce viz Konvoluční věta . Konvoluci lze naopak odvodit jako inverzní Fourierovu transformaci bodového součinu dvou Fourierových transformací.

Vizuální vysvětlení

Každou funkci vyjádřete pomocí fiktivní proměnné ${\ Displaystyle \ tau.}$ Odrážejte jednu z funkcí: →${\ displaystyle g (\ tau)}$${\ Displaystyle g (-\ tau).}$ Přidejte časový posun, t , který vám umožní klouzat podél osy.${\ Displaystyle g (t- \ tau)}$${\ displaystyle \ tau}$ Začněte t na −∞ a posuňte jej až na +∞ . Kdekoli se obě funkce protnou, najděte integrál jejich produktu. Jinými slovy, v čase t spočítejte plochu pod funkcí váženou funkcí vážení${\ Displaystyle f (\ tau)}$${\ Displaystyle g (t- \ tau).}$ Výsledný tvar vlny (zde není ukázán) je konvoluce funkcí f a g . Pokud f ( t ) je jednotkový impuls , výsledkem tohoto procesu je jednoduše g ( t ) . Formálně: ${\ Displaystyle \ int _ {-\ infty}^{\ infty} \ delta (\ tau) g (t- \ tau) \, d \ tau = g (t)}$
V tomto příkladu je červeně zbarvený „impuls“, je i funkce tak, konvoluce je ekvivalentní korelace. Snímek tohoto „filmu“ ukazuje funkce a (modře) pro určitou hodnotu parametru, která je libovolně definována jako vzdálenost od osy ke středu červeného impulsu. Množství žluté je plocha produktu vypočtená pomocí konvolučního/korelačního integrálu. Film vzniká nepřetržitou změnou a přepočítáním integrálu. Výsledek (zobrazený černě) je funkcí, ale je vykreslen na stejné ose jako pro pohodlí a srovnání. ${\ displaystyle \ g (\ tau),}$ ${\ Displaystyle (\ g (-\ tau) = g (\ tau) \),}$${\ Displaystyle g (t- \ tau)}$${\ Displaystyle f (\ tau)}$${\ displaystyle t,}$${\ displaystyle \ tau = 0}$${\ Displaystyle f (\ tau) \ cdot g (t- \ tau),}$${\ displaystyle t}$${\ displaystyle t,}$${\ displaystyle \ tau,}$
V tomto zobrazení, může představovat odezvu obvodu RC na úzkém impulsu, který se vyskytuje v Jinými slovy, je-li výsledkem konvoluce je jen Ale když je širší puls (červeně), odpověď je „rozmazaná“ verze Začíná na, protože jsme definovali jako vzdálenost od osy ke středu širokého impulzu (místo náběžné hrany). ${\ Displaystyle f (\ tau)}$${\ displaystyle \ tau = 0.}$${\ Displaystyle g (\ tau) = \ delta (\ tau),}$${\ Displaystyle f (t).}$${\ displaystyle g (\ tau)}$${\ Displaystyle f (t).}$${\ displaystyle t = -0,5,}$${\ displaystyle t}$${\ displaystyle \ tau = 0}$

Historický vývoj

Jedno z prvních použití konvolučního integrálu se objevilo v D'Alembertově odvození Taylorovy věty v Recherches sur différents points importants du système du monde, publikované v roce 1754.

Také výraz typu:

${\ Displaystyle \ int f (u) \ cdot g (xu) \, du}$

používá Sylvestre François Lacroix na straně 505 své knihy s názvem Pojednání o rozdílech a sériích , která je posledním ze 3 svazků encyklopedické řady: Traité du calcul différentiel et du calcul intégral , Chez Courcier, Paris, 1797–1800. Brzy poté se v dílech Pierra Simona Laplace , Jean-Baptiste Josepha Fouriera , Siméona Denise Poissona a dalších objevují konvoluční operace . Samotný termín se začal široce používat až v 50. nebo 60. letech minulého století. Předtím to bylo někdy známé jako Faltung (což v němčině znamená skládání ), kompoziční produkt , superpoziční integrál a Carsonův integrál . Přesto se zdá, že již v roce 1903, i když definice je ve starších použití poněkud neznámá.

Operace:

${\ Displaystyle \ int _ {0}^{t} \ varphi (s) \ psi (ts) \, ds, \ quad 0 \ leq t <\ infty,}$

je zvláštním případem kompozičních produktů uvažovaných italským matematikem Vito Volterrou v roce 1913.

Kruhová konvoluce

Když je funkce g _T periodická, s periodou T , pak pro funkce f , taková, že f ∗ g _T existuje, je konvoluce také periodická a identická s:

${\ Displaystyle (f*g_ {T}) (t) \ equiv \ int _ {t_ {0}}^{t_ {0}+T} \ left [\ sum _ {k =-\ infty}^{\ infty} f (\ tau +kT) \ right] g_ {T} (t- \ tau) \, d \ tau,}$

kde t ₀ je libovolná volba. Součtu se říká periodické součty funkce f .

Když g _T je periodické shrnutí jiné funkce g , pak f ∗ g _T je známé jako kruhová nebo cyklická konvoluce f a g .

A v případě, že periodické součet výše je nahrazena f _T , operace se nazývá periodická konvoluce f _T i g _T .

Diskrétní konvoluce

Pro komplexní hodnotou funkce f , g definované na množině Z celých čísel je diskrétní konvoluce o f a g je dána vztahem:

${\ Displaystyle (f*g) [n] = \ sum _ {m =-\ infty}^{\ infty} f [m] g [nm],}$

nebo ekvivalentně (viz komutativita ):

${\ Displaystyle (f*g) [n] = \ sum _ {m =-\ infty}^{\ infty} f [nm] g [m].}$

Konvoluce dvou konečných sekvencí je definována rozšířením sekvencí na konečně podporované funkce v sadě celých čísel. Když jsou sekvence koeficienty dvou polynomů , pak koeficienty běžného produktu těchto dvou polynomů jsou konvolucí původních dvou sekvencí. Toto je známé jako Cauchyho součin koeficientů sekvencí.

Když má tedy g v sadě konečnou podporu (představující například konečnou impulsní odezvu ), lze použít konečné součty: ${\ Displaystyle \ {-M, -M+1, \ tečky, M-1, M \}}$

${\ Displaystyle (f*g) [n] = \ sum _ {m = -M}^{M} f [nm] g [m].}$

Kruhová diskrétní konvoluce

Když je funkce g _N periodická, s periodou N , pak pro funkce f , taková, že f ∗ g _N existuje, je konvoluce také periodická a identická s:

${\ Displaystyle (f*g_ {N}) [n] \ equiv \ sum _ {m = 0}^{N-1} \ left (\ sum _ {k =-\ infty}^{\ infty} {f } [m+kN] \ vpravo) g_ {N} [nm].}$

Součet na k se nazývá periodické součty funkce f .

Pokud g _N je periodická součet jiné funkce, g , pak f * g _N je známý jako kruhová konvoluce o f a g .

Když jsou nenulové doby trvání f a g omezeny na interval [0, N -1] ,  f ∗ g _{N se} redukuje na tyto běžné formy:

${\ Displaystyle {\ begin {aligned} \ left (f*g_ {N} \ right) [n] & = \ sum _ {m = 0}^{N-1} f [m] g_ {N} [nm ] \\ & = \ součet _ {m = 0}^{n} f [m] g [nm]+\ součet _ {m = n+1}^{N-1} f [m] g [N+ nm] \\ [2pt] & = \ sum _ {m = 0}^{N-1} f [m] g [(nm) _ {\ bmod {N}}] \\ [2pt] & \ triangleq \ vlevo (f*_ {N} g \ vpravo) [n] \ konec {zarovnáno}}}$

( Rovnice 1 )

Notace ( f * _N g ) pro cyklické konvoluce značí konvoluce nad cyklické skupiny z celých čísel N .

Kruhová konvoluce vzniká nejčastěji v kontextu rychlé konvoluce s algoritmem rychlé Fourierovy transformace (FFT).

Algoritmy rychlé konvoluce

V mnoha situacích lze diskrétní konvoluce převést na kruhové konvoluce, takže k implementaci výpočtu lze použít rychlé transformace s konvoluční vlastností. Například konvoluce číslicových sekvencí je operace jádra při násobení víceciferných čísel, kterou lze tedy efektivně implementovat pomocí transformačních technik ( Knuth 1997 , §4.3.3.C; von zur Gathen & Gerhard 2003 , §8.2).

Eq.1 vyžaduje N aritmetických operací na výstupní hodnotu a N ² operací pro N výstupů. To lze výrazně snížit pomocí některého z několika rychlých algoritmů. Digitální zpracování signálu a další aplikace obvykle používají rychlé konvoluční algoritmy ke snížení nákladů na konvoluci nasložitostO ( N log N ).

Nejběžnější algoritmy rychlé konvoluce používají algoritmy rychlé Fourierovy transformace (FFT) prostřednictvím věty o kruhové konvoluci . Konkrétně je kruhová konvoluce dvou sekvencí konečné délky nalezena odebráním FFT každé sekvence, bodovým násobením a následným provedením inverzního FFT. Konvoluce výše definovaného typu jsou pak efektivně implementovány pomocí této techniky ve spojení s nulovým rozšířením a/nebo vyřazením částí výstupu. Jiné rychlé konvoluční algoritmy, jako je Schönhage -Strassenův algoritmus nebo Mersennova transformace, používají rychlé Fourierovy transformace v jiných prstencích .

Pokud je jedna sekvence mnohem delší než druhá, nulové prodloužení kratší sekvence a rychlá kruhová konvoluce nejsou výpočetně nejúčinnější dostupnou metodou. Místo toho dekompozice delší sekvence na bloky a svinutí každého bloku umožňuje rychlejší algoritmy, jako je metoda overlap – save a overlap – add . Metoda hybridní konvoluce, která kombinuje blokové a FIR algoritmy, umožňuje nulovou latenci vstupních a výstupních hodnot, která je užitečná pro konvoluční výpočty v reálném čase.

Definiční doména

Konvoluce dvou komplexně hodnocený funkcí na R ^d je sám o sobě komplexní hodnotou funkce na R ^d , definovaný:

${\ Displaystyle (f*g) (x) = \ int _ {\ mathbf {R} ^{d}} f (y) g (xy) \, dy = \ int _ {\ mathbf {R} ^{d }} f (xy) g (y) \, dy,}$

a je dobře definován pouze tehdy, pokud se f a g dostatečně rychle rozkládají v nekonečnu, aby integrál existoval. Podmínky pro existenci konvoluce mohou být složité, protože výbuch v g v nekonečnu lze snadno kompenzovat dostatečně rychlým rozpadem ve f . Otázka existence tedy může zahrnovat různé podmínky na f a g :

Kompaktně podporované funkce

Pokud f a g jsou kompaktně podporovány spojité funkce , pak existuje jejich konvoluce, a je také podporováno kompaktně a kontinuální ( Hörmander 1983 , kapitola 1). Obecněji řečeno, pokud je některá funkce (řekněme f ) kompaktně podporována a druhá je lokálně integrovatelná , pak je konvoluční f ∗ g dobře definovaná a spojitá.

Konvoluce f a g je také dobře definována, když jsou obě funkce lokálně čtvercové integrovatelné na R a podporované v intervalu tvaru [ a , +∞) (nebo obě podporované na [−∞, a ] ).

Integrovatelné funkce

Konvoluce f a g existuje, pokud f a g jsou obě Lebesgueovy integrovatelné funkce v L ¹ ( R ^d ) , a v tomto případě je f ∗ g také integrovatelné ( Stein & Weiss 1971 , Věta 1.3). To je důsledek Tonelliho věty . To platí také pro funkce v L ¹ , v rámci diskrétní konvoluce, nebo obecněji pro konvoluci v jakékoli skupině .

Podobně platí, že pokud f ∈ L ¹ ( R ^d ) a   g ∈ L ^p ( R ^d ) kde 1 ≤ p ≤ ∞ , pak   f ∗ g ∈ L ^p ( R ^d ), a

${\ Displaystyle \ | {f}*g \ | _ {p} \ leq \ | f \ | _ {1} \ | g \ | _ {p}.}$

V konkrétním případě p = 1 to ukazuje, že L ¹ je Banachova algebra pod konvolucí (a rovnost obou stran platí, pokud f a g nejsou záporné téměř všude).

Obecněji řečeno, Youngova nerovnost znamená, že konvoluce je spojitá bilineární mapa mezi vhodnými prostory L ^p . Konkrétně, pokud 1 ≤ p , q , r ≤ ∞ splňuje:

${\ displaystyle {\ frac {1} {p}}+{\ frac {1} {q}} = {\ frac {1} {r}}+1,}$

pak

${\ Displaystyle \ left \ Vert f*g \ right \ Vert _ {r} \ leq \ left \ Vert f \ right \ Vert _ {p} \ left \ Vert g \ right \ Vert _ {q}, \ quad f \ v {\ mathcal {L}}^{p}, \ g \ v {\ mathcal {L}}^{q},}$

takže konvoluce je spojité bilineární mapování od L ^p × L ^q do L ^r . Youngova nerovnost pro konvoluci platí také v jiných kontextech (kruhová skupina, konvoluce na Z ). Předchozí nerovnost není na skutečné přímce ostrá: když 1 < p , q , r <∞ , existuje konstanta B _{p , q} <1 taková, že:

${\ Displaystyle \ left \ Vert f*g \ right \ Vert _ {r} \ leq B_ {p, q} \ left \ Vert f \ right \ Vert _ {p} \ left \ Vert g \ right \ Vert _ { q}, \ quad f \ v {\ mathcal {L}}^{p}, \ g \ v {\ mathcal {L}}^{q}.}$

Optimální hodnota B _{p , q} byla objevena v roce 1975 a nezávisle v roce 1976, viz Brascamp – Liebova nerovnost .

Silnější odhad je pravdivý za předpokladu 1 < p , q , r <∞ :

${\ Displaystyle \ | f*g \ | _ {r} \ leq C_ {p, q} \ | f \ | _ {p} \ | g \ | _ {q, w}}$

kde je slabá norma L ^q . Konvoluce také definuje bilineární souvislou mapu pro , kvůli slabé Youngově nerovnosti: ${\ Displaystyle \ | g \ | _ {q, w}}$${\ Displaystyle L^{p, w} \ times L^{q, w} \ to L^{r, w}}$${\ Displaystyle 1 <p, q, r <\ infty}$

${\ Displaystyle \ | f*g \ | _ {r, w} \ leq C_ {p, q} \ | f \ | _ {p, w} \ | g \ | _ {r, w}.}$

Funkce rychlého rozpadu

Kromě kompaktně podporovaných funkcí a integrovatelných funkcí lze konvolvovat také funkce, které mají dostatečně rychlý rozpad v nekonečnu. Důležitým rysem konvoluce je, že pokud se f a g rychle rozpadají, pak se rychle rozpadá i f ∗ g . Zejména pokud f a g jsou rychle klesající funkce , pak je to také konvoluční f ∗ g . V kombinaci se skutečností, že konvoluce dochází k diferenciaci (viz #Vlastnosti ), vyplývá, že třída funkcí Schwartz je pod konvolucí uzavřena ( Stein & Weiss 1971 , Věta 3.3).

Distribuce

Za určitých okolností je možné definovat konvoluci funkce s distribucí nebo dvou distribucí. Pokud f je kompaktně podporovaná funkce a g je rozdělení, pak f ∗ g je hladká funkce definovaná distribučním vzorcem analogickým

${\ Displaystyle \ int _ {\ mathbf {R} ^{d}} {f} (y) g (xy) \, dy.}$

Obecněji je možné definici konvoluce rozšířit jedinečným způsobem tak, aby asociativní právo

${\ Displaystyle f*(g*\ varphi) = (f*g)*\ varphi}$

zůstává platný v případě, kde f je distribuce, a g kompaktně podporované rozdělení ( Hörmander 1983 , §4.2).

Opatření

Konvoluce jakýchkoli dvou opatření Borel u Stabilizátory a ν na konečnou variací je měřítkem definovaný ( Rudin 1962 ) ${\ Displaystyle \ mu *\ nu}$

${\ Displaystyle \ int _ {\ mathbf {R} ^{d}} f (x) \, d (\ mu *\ nu) (x) = \ int _ {\ mathbf {R} ^{d}} \ int _ {\ mathbf {R} ^{d}} f (x+y) \, d \ mu (x) \, d \ nu (y).}$

Zejména,

${\ Displaystyle (\ mu *\ nu) (A) = \ int _ {\ mathbf {R} ^{d} \ times \ mathbf {R} ^{d}} 1_ {A} (x+y) \, d (\ mu \ times \ nu) (x, y),}$

kde je měřitelná množina a je funkční ukazatel of . ${\ Displaystyle A \ subset \ mathbf {R} ^{d}}$${\ displaystyle 1_ {A}}$${\ displaystyle A}$

To souhlasí s výše definovanou konvolucí, když jsou μ a ν považovány za distribuce, stejně jako s konvolucí funkcí L ^1, když μ a ν jsou absolutně spojité s ohledem na Lebesgueovu míru.

Konvoluce opatření také splňuje následující verzi Youngovy nerovnosti

${\ Displaystyle \ | \ mu *\ nu \ | \ leq \ | \ mu \ | \ | \ nu \ |}$

kde normou je celková variace míry. Protože prostor opatření ohraničené variace je Banachovým prostorem , konvoluce opatření může být ošetřena standardními metodami funkční analýzy, které nemusí platit pro konvoluci distribucí.

Vlastnosti

Algebraické vlastnosti

Konvoluce definuje produkt na lineárním prostoru integrovatelných funkcí. Tento produkt splňuje následující algebraické vlastnosti, které formálně znamenají, že prostor integrovatelných funkcí s produktem daný konvolucí je komutativní asociativní algebra bez identity ( Strichartz 1994 , §3.3). Ostatní lineární prostory funkcí, jako je prostor spojitých funkcí kompaktní podpory, jsou pod konvolucí uzavřeny , a tak také tvoří komutativní asociativní algebry.

Komutativita

$${\ Displaystyle f*g = g*f}$$

Důkaz: Podle definice:

$${\ Displaystyle (f*g) (t) = \ int _ {-\ infty}^{\ infty} f (\ tau) g (t- \ tau) \, d \ tau}$$

Následuje změna proměnné integrace na výsledek.${\ Displaystyle u = t- \ tau}$

Asociativita

$${\ Displaystyle f*(g*h) = (f*g)*h}$$

Důkaz: Vyplývá to z použití Fubiniho věty (tj. Dvojité integrály lze vyhodnotit jako iterované integrály v libovolném pořadí).

Distribuce

$${\ Displaystyle f*(g+h) = (f*g)+(f*h)}$$

Důkaz: Vyplývá to z linearity integrálu.

Asociativita se skalárním násobením

$${\ Displaystyle a (f*g) = (af)*g}$$

pro jakékoli skutečné (nebo komplexní) číslo .${\ displaystyle a}$

Multiplikativní identita

Žádná algebra funkcí nemá identitu pro konvoluci. Nedostatek identity obvykle nepředstavuje zásadní nepříjemnost, protože většina sbírek funkcí, na nichž se konvoluce provádí, může být spojena s delta distribucí (unitární impuls se středem na nulu) nebo přinejmenším (jako je tomu v případě L ¹ ) připustit sbližování identity . Lineární prostor kompaktně podporovaných distribucí však přiznává identitu pod konvolucí. Konkrétně

$${\ Displaystyle f*\ delta = f}$$

kde δ je rozdělení delta.

Inverzní prvek

Některá rozdělení S mají pro konvoluci inverzní prvek S ^−1, který pak musí splňovat

$${\ Displaystyle S^{-1}*S = \ delta}$$

ze kterého lze získat explicitní vzorec pro S ⁻¹ .

Sada invertibilních distribucí tvoří v konvoluci abelianskou skupinu .

Složitá konjugace

${\ displaystyle {\ overline {f*g}} = {\ overline {f}}*{\ overline {g}}}$

Vztah s diferenciací

$${\ Displaystyle (f*g) '= f'*g = f*g '}$$

Důkaz:

$${\ Displaystyle {\ begin {aligned} (f*g) '& = {\ frac {d} {dt}} \ int _ {-\ infty}^{\ infty} f (\ tau) g (t- \ tau) \, d \ tau \\ [4pt] & = \ int _ {-\ infty}^{\ infty} f (\ tau) {\ frac {\ částečný} {\ částečný t}} g (t- \ tau) \, d \ tau \\ [4pt] & = \ int _ {-\ infty}^{\ infty} f (\ tau) g '(t- \ tau) \, d \ tau = f*g' . \ end {aligned}}}$$

Vztah s integrací

Kdyby a pak${\ textstyle F (t) = \ int _ {-\ infty}^{t} f (\ tau) d \ tau,}$${\ textstyle G (t) = \ int _ {-\ infty}^{t} g (\ tau) \, d \ tau,}$

$${\ Displaystyle (F*g) (t) = (f*G) (t) = \ int _ {-\ infty}^{t} (f*g) (\ tau) \, d \ tau.}$$

Integrace

Pokud f a g jsou integrovatelné funkce, pak integrál jejich konvoluce v celém prostoru jednoduše získáme jako součin jejich integrálů:

${\ Displaystyle \ int _ {\ mathbf {R} ^{d}} (f*g) (x) \, dx = \ left (\ int _ {\ mathbf {R} ^{d}} f (x) \, dx \ right) \ left (\ int _ {\ mathbf {R} ^{d}} g (x) \, dx \ right).}$

Vyplývá to z Fubiniho věty . Stejný výsledek platí, pokud jsou f a g pouze považovány za nezáporné měřitelné funkce podle Tonelliho věty .

Diferenciace

V případě jedné proměnné

${\ Displaystyle {\ frac {d} {dx}} (f*g) = {\ frac {df} {dx}}*g = f*{\ frac {dg} {dx}}}$

kde d / dx je derivát . Obecněji platí, že v případě funkcí několika proměnných platí analogický vzorec s parciální derivací :

${\ Displaystyle {\ frac {\ částečný} {\ částečný x_ {i}}} (f*g) = {\ frac {\ částečný f} {\ částečný x_ {i}}}*g = f*{\ frac {\ částečný g} {\ částečný x_ {i}}}.}$

Zvláštním důsledkem toho je, že na konvoluci lze pohlížet jako na „vyhlazovací“ operaci: konvoluce f a g je diferencovatelná tolikrát, kolikrát jsou f a g celkem.

Tyto identity platí za přesné podmínky, že f a g jsou absolutně integrovatelné a alespoň jedna z nich má absolutně integrovatelný (L ¹ ) slabý derivát, jako důsledek Youngovy konvoluční nerovnosti . Například když f je spojitě diferencovatelný s kompaktní podporou a g je libovolná lokálně integrovatelná funkce,

${\ Displaystyle {\ frac {d} {dx}} (f*g) = {\ frac {df} {dx}}*g.}$

Tyto identity také platí mnohem široce ve smyslu temperovaných distribucí, pokud jedna z f nebo g je rychle se snižující temperovaná distribuce , kompaktně podporovaná temperovaná distribuce nebo Schwartzova funkce a druhá je temperovaná distribuce. Na druhou stranu dvě pozitivní integrovatelné a nekonečně diferencovatelné funkce nemusí mít nikde souvislou konvoluci.

V diskrétním případě splňuje operátor rozdílu D f ( n ) = f ( n + 1) - f ( n ) analogický vztah:

${\ Displaystyle D (f*g) = (Df)*g = f*(Dg).}$

Konvoluční věta

Tyto konvoluční teorém se uvádí, že

${\ Displaystyle {\ mathcal {F}} \ {f*g \} = k \ cdot {\ mathcal {F}} \ {f \} \ cdot {\ mathcal {F}} \ {g \}}$

kde označuje Fourierovy transformace z , a je konstanta, která závisí na specifické normalizace Fourierovy transformace. Verze této věty platí také pro Laplaceovu transformaci , oboustrannou Laplaceovu transformaci , Z-transformaci a Mellinovu transformaci . ${\ displaystyle {\ mathcal {F}} \ {f \}}$${\ displaystyle f}$${\ displaystyle k}$

Na druhou stranu, pokud je Fourierova transformační matice , pak ${\ displaystyle {\ mathcal {W}}}$

${\ Displaystyle {\ mathcal {W}} \ left (C^{(1)} x \ ast C^{(2)} y \ right) = \ left ({\ mathcal {W}} C^{(1 )} \ bullet {\ mathcal {W}} C^{(2)} \ right) (x \ otimes y) = {\ mathcal {W}} C^{(1)} x \ circle {\ mathcal {W }} C^{(2)} y}$,

kde je produkt rozdělující obličej , označuje produkt Kronecker , označuje produkt Hadamard (tento výsledek je vývoj vlastností skici počtu ). ${\ displaystyle \ bullet}$${\ Displaystyle \ otimes}$${\ displaystyle \ circ}$

Translační ekvivalence

Konvoluce dojíždí s překlady, to znamená

${\ Displaystyle \ tau _ {x} (f*g) = (\ tau _ {x} f)*g = f*(\ tau _ {x} g)}$

kde τ _x f je překlad funkce f o x definovaný

${\ Displaystyle (\ tau _ {x} f) (y) = f (yx).}$

Pokud f je Schwartzova funkce , pak τ _x f je konvoluce s přeloženou Diracovou delta funkcí τ _x f = f ∗ τ _x δ . Translační invariance konvoluce Schwartzových funkcí je tedy důsledkem asociativity konvoluce.

Kromě toho je za určitých podmínek konvoluce nejobecnější translační invariantní operací. Neformálně řečeno platí následující

Předpokládejme, že S je omezený lineární operátor působící na funkce, které dojíždějí s překlady: S ( τ _x f ) = τ _x ( Sf ) pro všechna x . Poté je S uveden jako konvoluce s funkcí (nebo distribucí) g _S ; to je Sf = g _S ∗ f .

Některé překladově invariantní operace tedy mohou být reprezentovány jako konvoluce. Konvoluce hrají důležitou roli při studiu časově invariantních systémů a zejména teorie systému LTI . Zastupující funkce g _S je impulsní odezva transformačního S .

Přesnější verze výše citované věty vyžaduje určení třídy funkcí, na nichž je konvoluce definována, a také vyžaduje za předpokladu, že navíc musí být S spojitý lineární operátor s ohledem na příslušnou topologii . Je například známo, že každý spojitý lineární operátor invariantní s kontinuálním překladem na L ¹ je konvoluce s konečnou Borelskou mírou . Obecněji řečeno, každý spojitý lineární operátor invariantní s kontinuálním překladem na L ^p pro 1 ≤ p <∞ je konvoluce s temperovaným rozdělením, jehož Fourierova transformace je ohraničená. Všechny jsou dány ohraničenými Fourierovými multiplikátory .

Konvoluce o skupinách

Pokud G je vhodná skupina obdařená mírou λ a pokud f a g jsou skutečné nebo komplexně integrovatelné funkce na G , pak můžeme jejich konvoluci definovat

${\ Displaystyle (f*g) (x) = \ int _ {G} f (y) g \ left (y^{-1} x \ right) \, d \ lambda (y).}$

Obecně není komutativní. V typických případech zájmu je G lokálně kompaktní topologická skupina Hausdorff a λ je (vlevo) Haarova míra . V takovém případě, pokud G není unimodulární , konvoluce definovaná tímto způsobem není stejná jako . Upřednostňuje se jedno před druhým tak, aby konvoluce s pevnou funkcí g dojížděla s levým překladem ve skupině: ${\ textstyle \ int f \ left (xy^{-1} \ right) g (y) \, d \ lambda (y)}$

${\ Displaystyle L_ {h} (f*g) = (L_ {h} f)*g.}$

Kromě toho je konvence také vyžadována pro soulad s níže uvedenou definicí konvoluce opatření. Avšak u pravého namísto levého Haarova opatření je upřednostňován druhý integrál před prvním.

Na lokálně kompaktních abelianských skupinách platí verze konvoluční věty : Fourierova transformace konvoluce je bodovým součinem Fourierových transformací. Kruhu skupiny T s opatřením Lebesgue je okamžitá příkladem. Pro pevné g v L ¹ ( T ) máme následující známý operátor působící na Hilbertův prostor L ² ( T ):

${\ Displaystyle T {f} (x) = {\ frac {1} {2 \ pi}} \ int _ {\ mathbf {T}} {f} (y) g (xy) \, dy.}$

Obsluha T je kompaktní . Přímý výpočet ukazuje, že jeho pomocný T* je konvoluce s

${\ displaystyle {\ bar {g}} (-y).}$

Podle výše uvedené vlastnosti komutativity je T normální : T * T = TT *. Také T dojíždí s operátory překladu. Uvažujme rodinu S operátorů skládající se ze všech takových konvolucí a překladových operátorů. Pak S je dojíždějící rodina normálních operátorů. Podle spektrální teorii , existuje ortonormální báze { h _K }, který současně diagonalizes S . To charakterizuje závity na kruhu. Konkrétně máme

${\ Displaystyle h_ {k} (x) = e^{ikx}, \ quad k \ in \ mathbb {Z}, \;}$

které jsou přesně znaky z T . Každá konvoluce je na tomto základě kompaktním operátorem násobení . Na to lze pohlížet jako na verzi konvoluční věty diskutované výše.

Diskrétním příkladem je konečná cyklická skupina řádu n . Konvoluční operátory jsou zde reprezentovány cirkulačními maticemi a mohou být diagonalizovány diskrétní Fourierovou transformací .

Podobný výsledek platí pro kompaktní skupiny (ne nutně abelianské): maticové koeficienty konečných dimenzionálních unitárních reprezentací tvoří ortonormální základ v L ² podle Peter-Weylovy věty a analogie konvoluční věty nadále platí, spolu s mnoha další aspekty harmonické analýzy, které závisí na Fourierově transformaci.

Konvoluce opatření

Nechť G je (multiplikačně psaná) topologická skupina. Pokud μ a ν jsou konečné Borel opatření na G , pak jejich konvoluce μ * ν je definována jako pushforward opatření na skupinové akce a lze zapsat jako

${\ Displaystyle (\ mu *\ nu) (E) = \ iint 1_ {E} (xy) \, d \ mu (x) \, d \ nu (y)}$

pro každý měřitelná podmnožina E z G . Konvoluce je také konečným měřítkem, jehož celková variace vyhovuje

${\ Displaystyle \ | \ mu *\ nu \ | \ leq \ left \ | \ mu \ right \ | \ left \ | \ nu \ right \ |.}$

V případě, že je G lokálně kompaktní s (vlevo) Haarovou mírou λ a μ a ν jsou absolutně spojité vzhledem k λ, takže každý má funkci hustoty , pak je konvoluce μ ∗ ν také absolutně spojitá a jeho funkce hustoty je jen konvolucí dvou oddělených funkcí hustoty.

Pokud μ a ν jsou pravděpodobnostní míry na topologické skupině ( R , +), pak konvoluce μ ∗ ν je rozdělení pravděpodobnosti součtu X + Y dvou nezávislých náhodných proměnných X a Y, jejichž příslušná rozdělení jsou μ a ν.

Bialgebry

Nechť ( X , Δ, ∇, ε , η ) je bialgebra s násobením Δ, násobením ∇, jednotkou η a počítáním ε . Konvoluce je produkt definovaný na konci endomorfismu algebry End ( X ) následujícím způsobem. Nechť φ , ψ ∈ End ( X ), tj. Φ , ψ : X → X jsou funkce, které respektují veškerou algebraickou strukturu X , pak je konvoluce φ ∗ ψ definována jako složení

${\ Displaystyle X \ mathrel {\ xrightarrow {\ Delta}} X \ otimes X \ mathrel {\ xrightarrow {\ phi \ otimes \ psi}} X \ otimes X \ mathrel {\ xrightarrow {\ nabla}} X.}$

Konvoluce se objevuje zejména v definici Hopfových algeber ( Kassel 1995 , §III.3). Bialgebra je Hopfova algebra právě tehdy, pokud má antipod: endomorfismus S takový, že

${\ displaystyle S*\ operatorname {id} _ {X} = \ operatorname {id} _ {X}*S = \ eta \ circ \ varepsilon.}$

Aplikace

Gaussovské rozostření lze použít k získání hladkého digitálního obrazu polotónových výtisků ve stupních šedi .

Konvoluční a související operace se nacházejí v mnoha aplikacích ve vědě, strojírenství a matematice.

• Při zpracování obrazu

  Při zpracování digitálního obrazu hraje konvoluční filtrování důležitou roli v mnoha důležitých algoritmech při detekci hran a souvisejících procesech.

  V optice je fotografie bez zaostření konvolucí ostrého obrazu s funkcí objektivu. Fotografický termín pro toto je bokeh .

  V aplikacích pro zpracování obrazu, jako je přidání rozmazání.

• V digitálním zpracování dat

  V analytické chemii , Savitzky-Golay vyhlazovacích filtrů se používají pro analýzu spektroskopická data. Mohou zlepšit poměr signálu k šumu s minimálním zkreslením spekter

  Ve statistikách je vážený klouzavý průměr konvolucí.

• V akustice je dozvuk konvolucí původního zvuku s ozvěnami od předmětů obklopujících zdroj zvuku.

  Při zpracování digitálního signálu se konvoluce používá k mapování impulzní odezvy skutečné místnosti na digitální zvukový signál.

  V elektronické hudbě je konvoluce uložení spektrální nebo rytmické struktury zvuku. Tato obálka nebo struktura je často převzata z jiného zvuku. Konvoluce dvou signálů je filtrováním jednoho přes druhý.

• V elektrotechnice poskytuje konvoluce jedné funkce ( vstupního signálu ) s druhou funkcí (impulzní odezva) výstup lineárního časově invariantního systému (LTI). V každém daném okamžiku je výstup kumulovaným efektem všech předchozích hodnot vstupní funkce, přičemž největší vliv mají obvykle nejnovější hodnoty (vyjádřené jako multiplikativní faktor). Funkce impulzní odezvy poskytuje tento faktor jako funkci uplynulého času od okamžiku, kdy došlo ke každé vstupní hodnotě.
• Ve fyzice , kdekoli existuje lineární systém s „ principem superpozice “, se objeví konvoluční operace. Například při spektroskopickém rozšiřování čar v důsledku Dopplerova jevu dává samotný Gaussův spektrální tvar čáry a samotné kolizní rozšíření dává tvar Lorentzianovy čáry. Když jsou oba efekty operativní, tvar čáry je konvolucí Gaussova a Lorentzianova, Voigtova funkce .

  V časově rozlišené fluorescenční spektroskopii může být excitační signál zpracován jako řetězec delta pulzů a naměřená fluorescence je součtem exponenciálních rozpadů z každého delta pulsu.

  Ve výpočetní dynamiky tekutin je velký vířit simulace (LES) Model turbulence používá operace konvoluce snížit rozsah délkových stupnic nezbytných výpočtů a tím snižuje náklady na výpočetní.

• V teorii pravděpodobnosti je rozdělení pravděpodobnosti sumy dvou nezávislých náhodných proměnných je konvoluce jejich individuální distribucí.

  Při odhadu hustoty jádra se distribuce odhaduje z bodů vzorku pomocí konvoluce s jádrem, jako je izotropní Gaussian.

• V systémech plánování léčby radioterapií používá většina všech moderních výpočtových kódů algoritmus konvoluční superpozice .
• Ve strukturální spolehlivosti lze index spolehlivosti definovat na základě konvoluční věty.

  Definici indexu spolehlivosti pro funkce mezních stavů s nenormálními rozděleními lze stanovit odpovídající funkci společné distribuce . Ve skutečnosti lze společnou distribuční funkci získat pomocí konvoluční teorie.

• Konvoluční neurální sítě používají více kaskádových konvolučních jader s aplikacemi ve strojovém vidění a umělé inteligenci . Ačkoli se ve většině případů jedná spíše o vzájemné korelace než o spleti.
• V hydrodynamice vyhlazených částic se simulace dynamiky tekutin vypočítávají pomocí částic, z nichž každá má okolní jádra. Pro jakoukoli danou částici se nějaká fyzikální veličina vypočítá jako konvoluce s váhovou funkcí, kde označuje sousedy částice : ty, které se nacházejí v jejím jádře. Konvoluce je aproximována jako součet nad každým sousedem.${\ displaystyle i}$${\ displaystyle A_ {i}}$${\ displaystyle A_ {j}}$${\ displaystyle j}$${\ displaystyle i}$

Viz také

Poznámky

Reference

Další čtení

• Bracewell, R. (1986), Fourierova transformace a její aplikace (2. vydání), McGraw – Hill, ISBN 0-07-116043-4.
• Damelin, S .; Miller, W. (2011), Matematika zpracování signálu , Cambridge University Press, ISBN 978-1107601048
• Diggle, PJ (1985), „Kernel method for smoothing point process process data“, Journal of the Royal Statistical Society, Series C , 34 (2): 138–147, doi : 10.2307/2347366 , JSTOR  2347366 , S2CID  116746157
• Dominguez-Torres, Alejandro (2. listopadu 2010). „Původ a historie konvoluce“. 41 stran http://www.slideshare.net/Alexdfar/origin-adn-history-of-convolution . Cranfield, Bedford MK43 OAL, UK. Citováno 13. března 2013.
• Ghasemi, S. Hooman; Nowak, Andrzej S. (2017), „Reliability Index for Non-normal Distributions of Limit State Functions“, Structural Engineering and Mechanics , 62 (3): 365–372, doi : 10,12989/sem.2017.62.3.365
• Grinshpan, AZ (2017), „Nerovnost pro více konvolucí ve vztahu k Dirichletově pravděpodobnosti“, Advances in Applied Mathematics , 82 (1): 102–119, doi : 10,1016/j.aam.2016.08.001
• Hewitt, Edwin; Ross, Kenneth A. (1979), Abstraktní harmonická analýza. Sv. I , Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 115 (2. vyd.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-09434-0, MR  0551496.
• Hewitt, Edwin; Ross, Kenneth A. (1970), Abstraktní harmonická analýza. Sv. II: Struktura a analýza pro kompaktní skupiny. Analýza lokálně kompaktních abelianských skupin , Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlin, New York: Springer-Verlag , MR  0262773.
• Hörmander, L. (1983), Analýza lineárních parciálních diferenciálních operátorů I , Grundl. Matematika. Wissenschaft., 256 , Springer, doi : 10.1007/978-3-642-96750-4 , ISBN 3-540-12104-8, MR  0717035.
• Kassel, Christian (1995), Quantum groups , Graduate Texts in Mathematics, 155 , Berlin, New York: Springer-Verlag , doi : 10.1007/978-1-4612-0783-2 , ISBN 978-0-387-94370-1, MR  1321145.
• Knuth, Donald (1997), Seminumerické algoritmy (3. vyd.), Reading, Massachusetts: Addison – Wesley, ISBN 0-201-89684-2.
• Narici, Lawrence ; Beckenstein, Edward (2011). Topologické vektorové prostory . Čistá a aplikovaná matematika (druhé vydání.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC  144216834 .
• Reed, Michael; Simon, Barry (1975), Metody moderní matematické fyziky. II. Fourierova analýza, soběstačnost , New York-Londýn: Academic Press Harcourt Brace Jovanovich, Publishers, s. Xv+361, ISBN 0-12-585002-6, MR  0493420
• Rudin, Walter (1962), Fourierova analýza skupin , Interscience Tracts in Pure and Applied Mathematics, 12 , New York – London: Interscience Publishers, ISBN 0-471-52364-X, MR  0152834.
• Schaefer, Helmut H .; Wolff, Manfred P. (1999). Topologické vektorové prostory . GTM . 8 (druhé vydání.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC  840278135 .
• Stein, Elias ; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces , Princeton University Press, ISBN 0-691-08078-X.
• Sobolev, VI (2001) [1994], „Konvoluce funkcí“ , Encyklopedie matematiky , EMS Press.
• Strichartz, R. (1994), Průvodce distribuční teorií a Fourierovými transformacemi , CRC Press, ISBN 0-8493-8273-4.
• Titchmarsh, E (1948), Úvod do teorie Fourierových integrálů (2. vyd.), New York, NY: Chelsea Pub. Co. (vydáno 1986), ISBN 978-0-8284-0324-5.
• Trèves, François (2006) [1967]. Topologické vektorové prostory, distribuce a jádra . Mineola, NY: Dover Publications. ISBN 978-0-486-45352-1. OCLC  853623322 .
• Uludag, AM (1998), „O možném zhoršení hladkosti při operaci konvoluce“, J. Math. Anální. Appl. , 227 (2): 335–358, doi : 10,1006/jmaa.1998.6091
• von zur Gathen, J .; Gerhard, J. (2003), Modern Computer Algebra , Cambridge University Press, ISBN 0-521-82646-2.

externí odkazy

• Nejčasnější použití: Záznam o Convolution má několik historických informací.
• Konvoluce , na The Data Analysis BriefBook
• http://www.jhu.edu/~signals/convolve/index.html Vizuální konvoluce Java Applet
• http://www.jhu.edu/~signals/discreteconv2/index.html Vizuální konvoluce Applet Java pro funkce diskrétního času
• online kalkulačka https://get-the-solution.net/projects/discret-convolution discret-convolution
• https://lpsa.swarthmore.edu/Convolution/CI.html Konvoluční demo a vizualizace v javascriptu
• https://phiresky.github.io/convolution-demo/ Další demo konvoluce v javascriptu
• Přednášky o zpracování obrazu: Sbírka 18 přednášek ve formátu pdf z Vanderbilt University. Přednáška 7 je o 2-D konvoluci. , Alan Peters
• * https://archive.org/details/Lectures_on_Image_Processing
• Interaktivní výukový program Convolution Kernel Mask Operation
• Konvoluce na MathWorld
• Freeverb3 Impulse Response Processor : Opensource procesor s nulovou latencí impulsní odezva s doplňky VST
• Interaktivní Flash demo Stanford University CS 178 ukazující, jak funguje prostorová konvoluce.
• Video přednáška na téma konvoluce od Salmana Khana
• Příklad konvoluce FFT pro rozpoznávání vzorů (zpracování obrazu)
• Intuitivní průvodce konvolucí Blogpost o intuitivní interpretaci konvoluce.