Počitatelná sada - Countable set

„Počitatelné“ přeadresuje tady. Lingvistický koncept najdete v tématu hraběcí podstatné jméno . Politická mediální společnost viz Countable (aplikace) .
Nesmí být zaměňována s (rekurzivně) vyčíslitelnými sadami .

V matematiky , je počitatelné sada je sada se stejnou mohutnost ( počet prvků) jako nějakou podmnožinu množiny přirozených čísel . Počitatelná množina je buď konečná množina, nebo spočitatelně nekonečná množina. Ať už jsou konečné nebo nekonečné, prvky počitatelné množiny lze vždy počítat po jednom a - i když počítání nemusí nikdy skončit - každý prvek sady je spojen s unikátním přirozeným číslem.

Georg Cantor představil koncept počitatelných množin, kontrastních množin, které jsou počitatelné s těmi, které jsou nepočitatelné . Počítatelné množiny dnes tvoří základ oboru matematiky, kterému se říká diskrétní matematika .

Poznámka k terminologii

Ačkoli zde definované pojmy „počitatelné“ a „spočitatelně nekonečné“ jsou celkem běžné, terminologie není univerzální. Alternativní styl používá počitatelné to, co se zde nazývá spočitatelně nekonečné, a nanejvýš počitatelné znamená to, čemu se zde říká počitatelné. Abychom se vyhnuli nejasnostem, můžeme se omezit na výrazy „nanejvýš spočitatelné“ a „spočitatelně nekonečné“, ačkoli s ohledem na závěr je to nejhorší z obou světů. Pokud se čtenář v literatuře setká s pojmem „počitatelný“, doporučuje se zkontrolovat používanou definici.

Mohou být také použity pojmy vyjmenovatelné a vyčíslitelné , např. Odkazující na spočitatelné a spočitatelně nekonečné, ale jak se definice liší, čtenáři se opět doporučuje zkontrolovat používanou definici.

Definice

Nejvýstižnější definice je z hlediska mohutnosti . Sada S je počitatelná, pokud je její mohutnost | S | je menší než nebo rovno ( Aleph-null ), mohutnost množiny přirozených čísel N . Množina S je spočítatelně nekonečná, pokud | S | = . Sada je nepočítatelná, pokud není spočitatelná, tj. Její mohutnost je větší než ; čtenář je odkázán na sadu Uncountable pro další diskusi.

Ekvivalentně je množina S počitatelná, pokud :

Podobně je množina S spočitatelně nekonečná, pokud :

  • mezi S a N existuje injektivní a surjektivní (a tedy bijektivní ) mapování . Jinými slovy, sada je countably nekonečná, pokud má jedna k jedné korespondenci s přírodním sadě čísel, N .
  • Prvky S mohou být uspořádány v nekonečné posloupnosti , kde je odlišný od pro a každý prvek S je uveden.

Dějiny

V roce 1874 ve svém prvním článku o teorii množin Cantor dokázal, že množina reálných čísel je nepočitatelná, což ukazuje, že ne všechny nekonečné množiny jsou spočitatelné. V roce 1878 použil korespondence jeden na jednoho k definování a porovnání kardinalit. V roce 1883 rozšířil přirozená čísla svými nekonečnými řadovými čísly a použil množiny řadových čísel k vytvoření nekonečna množin s různými nekonečnými kardinalitami.

Úvod

Sada je soubor prvků , a může být popsán mnoha způsoby. Jedním ze způsobů je jednoduše vyjmenovat všechny jeho prvky; například sada sestávající z celých čísel 3, 4 a 5 může být označena {3, 4, 5}, nazývaná forma seznamu. Toto je však účinné pouze pro malé sady; u větších sad by to bylo časově náročné a náchylné k chybám. Místo výčtu každého jednotlivého prvku se někdy používá elipsa („...“), která představuje mnoho prvků mezi počátečním prvkem a koncovým prvkem v sadě, pokud pisatel věří, že čtenář snadno uhodne, co ... představuje ; například {1, 2, 3, ..., 100} pravděpodobně označuje množinu celých čísel od 1 do 100. I v tomto případě je však stále možné uvést všechny prvky, protože počet prvků v sada je konečná.

Některé sady jsou nekonečné ; tyto sady mají více než n prvků, kde n je jakékoli celé číslo, které lze zadat. (Bez ohledu na to, jak velké je zadané celé číslo n , například n = 9 × 10 32 , nekonečné množiny mají více než n prvků.) Například množina přirozených čísel, označitelná jako {0, 1, 2, 3, 4 , 5, ...}, má nekonečně mnoho prvků a pro jeho velikost nemůžeme použít žádné přirozené číslo. Nicméně se ukazuje, že nekonečné množiny mají přesně definovaný pojem velikosti (nebo přesněji, mohutnosti , odborného výrazu pro počet prvků v sadě), a ne všechny nekonečné množiny mají stejnou mohutnost.

Bijektivní mapování z celých čísel na sudá čísla

Abychom pochopili, co to znamená, nejprve zkoumat, co to nebude znamenat. Například existuje nekonečně mnoho lichých celých čísel, nekonečně mnoho sudých celých čísel a (tedy) celkově nekonečně mnoho celých čísel. Ukazuje se však, že počet sudých celých čísel, který je stejný jako počet lichých celých čísel, je také stejný jako celkový počet celých čísel. Je to proto, že můžeme zařídit věci tak, že pro každé celé číslo existuje odlišné sudé číslo:

nebo obecněji (viz obrázek). To, co jsme zde udělali, je uspořádat celá čísla a sudá celá čísla do korespondence jedna k jedné (neboli bijection ), což je funkce, která mapuje mezi dvěma množinami tak, že každý prvek každé sady odpovídá jednomu prvku v druhé soubor.

Ne všechny nekonečné množiny však mají stejnou mohutnost. Například Georg Cantor (který představil tento koncept) prokázal, že skutečná čísla nelze dávat do vzájemné korespondence s přirozenými čísly (nezáporná celá čísla), a proto má množina reálných čísel větší mohutnost než množina přirozených čísel.

Formální přehled

Podle definice, soubor S je spočetná , když existuje prosté zobrazení f  : S → N z S na přirozených čísel N = {0, 1, 2, 3, ...}. To potom znamená, že každý prvek S má korespondenci na jiný prvek v N .

Může se zdát přirozené rozdělit sady do různých tříd: dát dohromady všechny sady obsahující jeden prvek; všechny sady obsahující dva prvky dohromady; ...; nakonec dejte dohromady všechny nekonečné množiny a považujte je za stejně velké. Tento pohled je však při přirozené definici velikosti neudržitelný.

Abychom to rozvinuli, potřebujeme koncept bijekce . Ačkoli se „bijekce“ může zdát pokročilejším pojmem než číslo, obvyklý vývoj matematiky z hlediska teorie množin definuje funkce před čísly, protože jsou založeny na mnohem jednodušších množinách. Zde přichází na řadu koncept bijekce: definujte korespondenci

a ↔ 1, b ↔ 2, c ↔ 3

Protože každý prvek { a , b , c } je spárován právě s

jedním prvkem {1, 2, 3} a naopak, definuje to bijekci.

Nyní tuto situaci zobecňujeme; můžeme definovat , že dva soubory mají stejnou velikost, tehdy a jen tehdy, pokud existuje bijekce mezi nimi. U všech konečných množin nám to dává obvyklou definici „stejné velikosti“.

Pokud jde o nekonečné množiny, zvažte množiny A = {1, 2, 3, ...}, množinu kladných celých čísel a B = {2, 4, 6, ...}, množinu sudých kladná celá čísla. Tvrdíme, že podle naší definice mají tyto sady stejnou velikost, a proto je B spočitatelně nekonečné. Připomeňme si, že abychom to dokázali, musíme mezi nimi ukázat bijekci. Toho lze dosáhnout přiřazením n ↔ 2 n , takže

1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....

Stejně jako v předchozím příkladu byl každý prvek A spárován s přesně jedním prvkem B a naopak. Proto mají stejnou velikost. Toto je příklad sady stejné velikosti jako jedna z jejích vlastních podmnožin , což je u konečných sad nemožné.

Stejně tak množina všech uspořádaných dvojic přirozených čísel ( karteziánský součin dvou množin přirozených čísel, N × N ) je spočítatelně nekonečná, jak je vidět na cestě podobné té na obrázku:

Funkce párování Cantor přiřadí každému páru přirozených čísel jedno přirozené číslo

Výsledné mapování probíhá následovně:

0 ↔ (0, 0), 1 ↔ (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), ....

Toto mapování pokrývá všechny takto seřazené páry.

Tato forma trojúhelníkového mapování rekurzivně generalizuje na n - tice přirozených čísel, tj. ( A 1 , a 2 , a 3 , ..., a n ) kde a i a n jsou přirozená čísla, opakovaným mapováním prvních dvou prvků z n -tuple k přirozené číslo. Například (0, 2, 3) lze zapsat jako ((0, 2), 3). Potom (0, 2) mapuje na 5, takže ((0, 2), 3) mapuje na (5, 3), pak (5, 3) mapuje na 39. Vzhledem k jiné 2-tice, to je pár, jako je ( a , b ), mapuje na jiné přirozené číslo, rozdíl mezi dvěma n-ticemi jedním prvkem stačí k zajištění mapování n-tic na různá přirozená čísla. Je tedy prokázána injekce ze sady n -tuples do množiny přirozených čísel N. Pro množinu n-tic vytvořených karteziánským součinem konečných mnoha různých množin má každý prvek v každé n-tici korespondenci s přirozeným číslem, takže každé n-tice lze zapsat přirozenými čísly, pak se pro potvrzení věty použije stejná logika .

Věta: Kartézský součin z finitely mnoha spočetné množiny je spočetný.

Množina všech celá čísla Z a soubor všech racionálních čísel Q může intuitivně zdát mnohem větší než N . Ale zdání může klamat. Je-li dvojice působí jako čitatele a jmenovatele části vulgární frakce (frakce ve formě a / b , kde a

b * 0 jsou celá čísla), pak pro každé pozitivní frakce, můžeme přijít s zřetelným přirozené číslo odpovídající k tomu. Tato reprezentace také zahrnuje přirozená čísla, protože každé přirozené číslo je také zlomek N /1. Můžeme tedy usoudit, že existuje přesně tolik kladných racionálních čísel, kolik je kladných celých čísel. To platí také pro všechna racionální čísla, jak je vidět níže.

Věta: Z (množina všech celých čísel) a Q (množina všech racionálních čísel) jsou počitatelné.

Podobným způsobem lze spočítat množinu algebraických čísel .

Někdy je užitečné více než jedno mapování: sada A, která má být zobrazena jako počitatelná, je mapována jedna ku jedné (injekce) do jiné sady B, pak je A prokázána jako spočítatelná, pokud je B mapována jedna k jedné do množiny přirozená čísla. Například sadu kladných racionálních čísel lze snadno mapovat jedna k jedné do sady párů přirozených čísel (2-tice), protože p / q mapuje na ( p , q ). Vzhledem k tomu, že množina párů přirozených čísel je mapována jedna ku jedné (ve skutečnosti korespondence nebo bijekce jedna k jedné) do množiny přirozených čísel, jak je uvedeno výše, pozitivní racionální množina čísel se prokáže jako spočitatelná.

Věta: Každé konečné spojení počitatelných množin je spočitatelné.

S předvídavostí vědomí, že existují nespočetné množiny, si můžeme klást otázku, zda lze tento poslední výsledek posunout dále. Odpověď zní „ano“ a „ne“, můžeme ji rozšířit, ale musíme k tomu předpokládat nový axiom.

Věta: (Za předpokladu axiomu počitatelné volby ) Spojení spočitatelných mnoha počitatelných množin je spočitatelné.

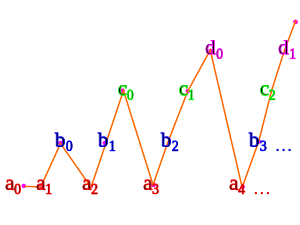
Například dané počitatelné sady a , b , c , ...

Výčet pro počitatelný počet počitatelných sad

Pomocí varianty trojúhelníkového výčtu jsme viděli výše:

  • a 0 mapuje na 0
  • a 1 mapuje na 1
  • b 0 mapuje na 2
  • a 2 mapuje na 3
  • b 1 mapuje na 4
  • c 0 mapuje na 5
  • a 3 mapy na 6
  • b 2 mapy na 7
  • c 1 mapuje na 8
  • d 0 mapuje na 9
  • a 4 mapy na 10
  • ...

To funguje pouze v případě, že sady a , b , c , ... jsou nesouvislé . Pokud ne, pak je unie ještě menší, a je tedy také započítatelná podle předchozí věty.

K indexování

všech množin a , b , c , ... potřebujeme axiom spočitatelné volby .

Věta: Množinu všech konečných sekvencí přirozených čísel lze spočítat.

Tato sada je spojením sekvencí délky 1, sekvencí délky 2 a sekvencí délky 3, z nichž každá je spočítatelná množina (konečný karteziánský součin). Mluvíme tedy o spočitatelném svazku počitatelných množin, který je započítatelný předchozí větou.

Věta: Množina všech konečných podmnožin přirozených čísel je spočitatelná.

Prvky jakékoli konečné podmnožiny lze uspořádat do konečné sekvence. Existuje pouze spočitatelně mnoho konečných sekvencí, takže také existuje pouze spočitatelně mnoho konečných podmnožin.

Věta: Nechť S a T jsou množiny.

  1. Pokud je funkce f  : S → T injektivní a T je počitatelné, pak S je počitatelné.
  2. Pokud je funkce g  : S → T surjektivní a S je počitatelná, pak T je počitatelná.

Ty vyplývají z definic počitatelné množiny jako injektivní / surjektivní funkce.

Cantorova věta tvrdí, že pokud A je množina a P ( A ) je její mocnina , tj. Množina všech podmnožin A , pak neexistuje žádná surjektivní funkce od A do P ( A ). Důkaz je uveden v článku Cantorova věta . Jako bezprostřední důsledek toho a výše uvedené základní věty máme:

Tvrzení: Množina P ( N ) se nedá spočítat; tj. je nepočítatelný .

Rozpracování tohoto výsledku viz Cantorův diagonální argument .

Množina reálných čísel je nepočitatelná, stejně jako množina všech nekonečných posloupností přirozených čísel.

Minimální model teorie množin je počitatelný

Pokud existuje množina, která je standardním modelem (viz vnitřní model ) teorie množin ZFC, pak existuje minimální standardní model ( viz Konstruovatelný vesmír ). Pomocí věty Löwenheim – Skolem lze ukázat, že tento minimální model je počitatelný. Skutečnost, že pojem „nepočítatelnosti“ má smysl i v tomto modelu, a zejména v tom, že tento model M obsahuje prvky, které jsou:

  • podmnožiny M , tedy počitatelné,
  • ale nepočitatelné z hlediska M ,

byl v počátcích teorie množin považován za paradoxní, více viz Skolemův paradox .

Minimální standardní model obsahuje všechna algebraická čísla a všechna efektivně vyčíslitelná transcendentální čísla , stejně jako mnoho dalších druhů čísel.

Celkový počet objednávek

Počitatelné sady lze zcela objednat různými způsoby, například:

  • Objednávky studny (viz také pořadové číslo ):
    • Obvyklé pořadí přirozených čísel (0, 1, 2, 3, 4, 5, ...)
    • Celá čísla v pořadí (0, 1, 2, 3, ...; −1, −2, −3, ...)
  • Další ( špatně objednané):
    • Obvyklé pořadí celých čísel (..., −3, −2, −1, 0, 1, 2, 3, ...)
    • Obvyklé pořadí racionálních čísel (Nelze explicitně zapsat jako seřazený seznam!)

V obou příkladech řádů vrtů zde má jakákoli podmnožina nejmenší prvek ; a v obou příkladech objednávek, které se netýkají dobře, některé podmnožiny nemají nejmenší prvek . Toto je klíčová definice, která určuje, zda je celková objednávka také objednávkou vrtu.

Viz také

Poznámky

Citace

Reference