Bravaisova mříž - Bravais lattice

V geometrii a krystalografii je Bravaisova mříž , pojmenovaná po Auguste Bravaisovi ( 1850 ), nekonečná řada diskrétních bodů generovaných sadou diskrétních translačních operací popsaných v trojrozměrném prostoru:

{\ Displaystyle \ mathbf {R} = n_ {1} \ mathbf {a} _ {1}+n_ {2} \ mathbf {a} _ {2}+n_ {3} \ mathbf {a} _ {3} }

kde n _i jsou libovolná celá čísla a a _i jsou primitivní translační vektory nebo primitivní vektory, které leží v různých směrech (ne nutně vzájemně kolmých) a pokrývají mřížku. Volba primitivních vektorů pro danou Bravaisovu mřížku není ojedinělá. Zásadním aspektem jakékoli Bravaisovy mřížky je, že při jakékoli volbě směru se mřížka bude při pohledu v tomto zvoleném směru zdát úplně stejná z každého z diskrétních bodů mřížky.

Bravaisova mřížková koncepce se používá k formálnímu definování krystalického uspořádání a jeho (konečných) hranic. Krystal se skládá z jednoho nebo více atomů, nazvaný základ nebo motiv , v každém bodě mřížky. Základ se může skládat z atomů , molekul , nebo polymerní řetězce pevných látek , a mřížka zajišťuje umístění základě.

Dvě mřížky Bravais jsou často považovány za ekvivalentní, pokud mají skupiny izomorfní symetrie. V tomto smyslu existuje 5 možných Bravaisových mřížek ve 2-dimenzionálním prostoru a 14 možných Bravaisových mřížek v trojrozměrném prostoru. 14 možných skupin symetrie Bravaisových mřížek je 14 z 230 vesmírných skupin . V kontextu klasifikace vesmírných skupin se mřížkám Bravais také říká Bravaisovy třídy, Bravaisovy aritmetické třídy nebo Bravaisova hejna.

Jednotková buňka

V krystalografii existuje koncept jednotkové buňky, která zahrnuje prostor mezi sousedními body mřížky a také všechny atomy v tomto prostoru. Jednotková buňka je definována jako prostor, který při překladu podskupinou všech popsaných vektorů vyplňuje prostor mřížky bez překrývání nebo prázdnoty. (Tj., Mřížkový prostor je násobkem jednotkové buňky.) Existují hlavně dva typy jednotkových buněk: primitivní jednotkové buňky a konvenční jednotkové buňky. Primitivní buňka je úplně nejmenší složkou mřížky (nebo krystalu), která při skládání společně s translačními operacemi mřížky reprodukuje celou mřížku (nebo krystal). Všimněte si, že překlady musí být mřížkovými překladovými operacemi, které způsobí, že se mřížka po překladu zobrazí beze změny. Pokud by byly povoleny libovolné překlady, bylo by možné vytvořit primitivní buňku o polovinu menší než skutečnou a přeložit jako příklad dvakrát častěji. Dalším způsobem, jak definovat velikost primitivní buňky, která se vyhýbá vyvolávání translačních operací mřížky, je říci, že primitivní buňka je nejmenší možná složka mřížky (nebo krystalu), kterou lze opakovat za účelem reprodukce celé mřížky (nebo krystalu), a to obsahuje přesně jeden mřížkový bod. V obou definicích je primitivní buňka charakterizována svou malou velikostí. Existuje zjevně mnoho možností buňky, která dokáže při skládání reprodukovat celou mřížku (například dvě poloviny mřížky) a požadavek na minimální velikost odlišuje primitivní buňku od všech těchto ostatních platných opakujících se jednotek. Pokud je mřížka nebo krystal 2-dimenzionální, má primitivní buňka minimální plochu; podobně ve 3 rozměrech má primitivní buňka minimální objem. Navzdory tomuto přísnému požadavku na minimální velikost neexistuje jediná jedinečná volba primitivní jednotkové buňky. Ve skutečnosti všechny buňky, jejichž hranice jsou primitivními translačními vektory, budou primitivní jednotkové buňky. Skutečnost, že pro danou mřížku neexistuje jedinečná volba primitivních translačních vektorů, vede k multiplicitě možných primitivních jednotkových buněk. Konvenční jednotkové buňky na druhé straně nemusí být nutně buňkami minimální velikosti. Vybírají se čistě pro pohodlí a často se používají pro ilustrační účely. Jsou volně definovány. ${\ Displaystyle \ mathbf {R} = n_ {1} \ mathbf {a} _ {1}+n_ {2} \ mathbf {a} _ {2}+n_ {3} \ mathbf {a} _ {3} }$

Primitivní jednotkové buňky jsou definovány jako jednotkové buňky s nejmenším objemem pro daný krystal. (Krystal je mřížka a základ v každém bodu mřížky.) Aby měl primitivní jednotkový článek nejmenší objem buňky, musí obsahovat (1) pouze jeden bod mřížky a (2) minimální množství základních složek (např. počet atomů v základu). Pro první požadavek je počítání počtu mřížkových bodů v jednotkové buňce takové, že pokud je mřížkový bod sdílen m sousedními jednotkovými buňkami kolem tohoto mřížkového bodu, pak se bod počítá jako 1/ m . Druhý požadavek je nezbytný, protože existují krystaly, které lze popsat více než jednou kombinací mřížky a báze. Například krystal, viděný mřížkou s atomy jednoho druhu umístěnými v každém bodě mřížky (nejjednodušší základní forma), může být také viděn jinou mřížkou na základě dvou atomů. V tomto případě je primitivní jednotková buňka jednotková buňka, která má pouze jeden bod mřížky v prvním způsobu popisu krystalu, aby byl zajištěn nejmenší objem jednotkové buňky.

Může existovat více než jeden způsob výběru primitivní buňky pro daný krystal a každá volba bude mít jiný tvar primitivní buňky, ale objem primitivní buňky je pro každou volbu stejný a každá volba bude mít tu vlastnost, že -jedna korespondence může být stanovena mezi primitivními jednotkovými buňkami a diskrétními mřížkovými body nad přidruženou mřížkou. Všechny primitivní jednotkové buňky s různými tvary pro daný krystal mají podle definice stejný objem; Pokud pro daný krystal platí, že n je hustota bodů mřížky v mřížce zajišťující minimální množství základních složek a v je objem zvolené primitivní buňky, pak nv = 1, což má za následek v = 1/ n , takže každá primitivní buňka má stejný objem 1/ n .

Ze všech možných primitivních buněk pro daný krystal může být zřejmou primitivní buňkou rovnoběžnostěnka tvořená zvolenou sadou primitivních translačních vektorů. (Opět platí, že tyto vektory musí vytvořit mřížku s minimálním množstvím základních složek.) Tedy množina všech bodů, kde a je zvolený primitivní vektor. Tato primitivní buňka ne vždy ukazuje jasnou symetrii daného krystalu. V tomto případě se často používá konvenční jednotková buňka snadno zobrazující krystalovou symetrii. Konvenční objem jednotkové buňky bude celočíselným násobkem primitivního objemu jednotkové buňky. ${\ Displaystyle \ mathbf {r} = x_ {1} \ mathbf {a} _ {1}+x_ {2} \ mathbf {a} _ {2}+x_ {3} \ mathbf {a} _ {3} }$ ${\ Displaystyle 0 \ leq x_ {i} <1}$ ${\ displaystyle \ mathbf {a} _ {i}}$

Původ konceptu

Ve dvou rozměrech lze libovolnou mřížku určit délkou jejích dvou primitivních translačních vektorů a úhlem mezi nimi. Existuje nekonečný počet možných mřížek, které lze tímto způsobem popsat. Je žádoucí nějaký způsob kategorizace různých typů mřížek. Jedním ze způsobů, jak toho dosáhnout, je rozpoznat, že některé mříže mají inherentní symetrii. Lze stanovit podmínky pro délku primitivních translačních vektorů a pro úhel mezi nimi pro vytváření různých symetrických mřížek. Tyto symetrie jsou kategorizovány do různých typů, jako jsou zrcadlové symetrie, inverzní symetrie, rotační symetrie a translační symetrie. Konkrétní kombinace těchto symetrií (například dvojnásobná rotační symetrie a zrcadlová symetrie) se nazývá bodová skupina . Mříže lze tedy kategorizovat podle toho, jaká bodová skupina se na ně vztahuje. Nejzákladnější bodová skupina odpovídá rotační invarianci pod 2π a π, nebo 1- a 2násobné rotační symetrii. To ve skutečnosti platí automaticky pro všechny 2-dimenzionální mřížky a je to nejobecnější bodová skupina. Mříže obsažené v této skupině (technicky všechny mříže, ale obvykle všechny mříže, které nespadají do žádné jiné skupiny bodů) se nazývají šikmé mříže . Odtamtud jsou ve dvou dimenzích další 4 bodové skupiny (nebo ekvivalentně 4 typy omezení délek/úhlů primitivních translačních vektorů), které odpovídají 4 zbývajícím kategoriím mřížky: čtvercový, šestihranný, obdélníkový a středový obdélníkový . Celkem tedy existuje 5 Bravaisových mřížek ve 2 rozměrech. Podobně ve 3 rozměrech existuje 14 mřížek Bravais: 1 obecná kategorie „odpadkový koš“ ( tříkolka ) a 13 dalších kategorií. Těchto 14 typů mřížek je dále pohodlně seskupeno do 7 mřížkových systémů (triklinické, monoklinické, ortorombické, tetragonální, kubické, trigonální a hexagonální).

Ve 2 rozměrech

Ve dvourozměrném prostoru je 5 Bravaisových mřížek, seskupených do čtyř krystalových rodin .

Poznámka: V diagramech jednotkových buněk v následující tabulce jsou body mřížky znázorněny pomocí černých kruhů a buňky buněk jsou zobrazeny pomocí rovnoběžníků (což mohou být čtverce nebo obdélníky) vyznačené černě. Ačkoli každý ze čtyř rohů každého rovnoběžníku navazuje na bod mřížky, pouze jeden ze čtyř bodů mřížky technicky patří k dané jednotkové buňce a každý z dalších tří bodů mřížky patří k jedné ze sousedních jednotkových buněk. To lze vidět na představě, jak se pohybuje rovnoběžník jednotkové buňky mírně doleva a mírně dolů, přičemž všechny černé kruhy bodů mřížky zůstávají pevné.

Krystalová rodina	Bodová skupina ( Schönfliesova notace )	5 mříží Bravais
Krystalová rodina	Bodová skupina ( Schönfliesova notace )	Primitivní (p)	Na střed (c)
Monoklinika (m)	C ₂	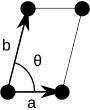Šikmý (mp)
Orthorhombic (o)	D ₂	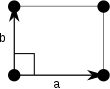Obdélníkový (op)	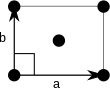Vycentrovaný obdélníkový (oc)
Tetragonal (t)	D ₄	Náměstí (tp)
Šestihranný (h)	D ₆	Šestihranný (hp)

Jednotkové buňky jsou specifikovány podle relativních délek okrajů buněk ( a a b ) a úhlu mezi nimi ( θ ). Plochu jednotkové buňky lze vypočítat vyhodnocením normy || a × b || , kde a a b jsou mřížkové vektory. Vlastnosti krystalových rodin jsou uvedeny níže:

Krystalová rodina	Plocha	Osové vzdálenosti (délky hran)	Axiální úhel
Monoklinika	${\ Displaystyle ab \, \ sin \ theta}$	a ≠ b	θ ≠ 90 °
Orthorhombic	${\ Displaystyle ab}$	a ≠ b	θ = 90 °
Tetragonální	${\ displaystyle a^{2}}$	a = b	θ = 90 °
Šestihranný	${\ displaystyle {\ frac {\ sqrt {3}} {2}} \, a^{2}}$	a = b	θ = 120 °

Ve 3 rozměrech

2 × 2 × 2 jednotkové buňky diamantové krychlové mřížky

V trojrozměrném prostoru je 14 mřížek Bravais. Ty se získají kombinací jednoho ze sedmi mřížkových systémů s jedním z typů centrování. Typy centrování identifikují umístění bodů mřížky v jednotkové buňce následovně:

Primitivní (P): mřížkové body pouze v rozích buněk (někdy se nazývá jednoduché)
Základna se středem (A, B nebo C): body mřížky v rozích buněk s jedním dalším bodem ve středu každé plochy jedné dvojice rovnoběžných ploch buňky (někdy se nazývá střed s koncem)
Body-centered (I): body mřížky v rozích buněk, s jedním dalším bodem uprostřed buňky
Na střed obličeje (F): mřížkové body v rozích buněk s jedním dalším bodem ve středu každé z ploch buňky

K popisu všech možných mřížek nejsou zapotřebí všechny kombinace mřížkových systémů a typů centrování, protože je možné ukázat, že některé z nich jsou ve skutečnosti navzájem ekvivalentní. Například monoklinická mřížka I může být popsána monoklinickou mřížkou C různým výběrem krystalových os. Podobně mohou být všechny mříže se středem A nebo B popsány buď C-nebo P-středěním. Tím se sníží počet kombinací na 14 konvenčních mřížek Bravais, uvedených v tabulce níže. Pod každým diagramem je Pearsonův symbol pro Bravaisovu mřížku.

Poznámka: V diagramech jednotkových buněk v následující tabulce jsou zobrazeny všechny body mřížky na hranici buňky (rohy a plochy); ne všechny tyto mřížové body však technicky patří do dané jednotkové buňky. To lze vidět na představě, jak se jednotková buňka mírně pohybuje v záporném směru každé osy, přičemž body mřížky zůstávají pevné. Zhruba řečeno, lze to považovat za posunutí buňky jednotky mírně doleva, mírně dolů a mírně mimo obrazovku. To ukazuje, že pouze jeden z osmi rohových mřížových bodů (konkrétně přední, levý, spodní) náleží dané jednotkové buňce (dalších sedm bodů mřížky patří sousedním jednotkovým buňkám). Do dané jednotkové buňky navíc patří pouze jeden ze dvou bodů mřížky zobrazených na horním a dolním povrchu ve sloupci se středem základny . Nakonec do dané jednotkové buňky patří pouze tři ze šesti bodů mřížky na plochách ve sloupci na střed plochy .

Krystalová rodina	Mřížkový systém	Bodová skupina ( Schönfliesova notace )	14 mříží Bravais
Krystalová rodina	Mřížkový systém	Bodová skupina ( Schönfliesova notace )	Primitivní (P)	Základna-střed (S)	Tělo-střed (I)	Na střed obličeje (F)
Triclinic (a)		C _i	aP
Monoklinika (m)		C _2h	mP	slečna
Orthorhombic (o)		D _2h	oP	oS	oI	z
Tetragonal (t)		D _4h	tP		tI
Šestihranný (h)	Kosočtverečný	D _3d	hR
Šestihranný (h)	Šestihranný	D _6h	hP
Krychlový (c)		O _h	cP		cI	cF

Jednotkové buňky jsou specifikovány podle šesti parametrů mřížky, což jsou relativní délky okrajů buněk ( a , b , c ) a úhly mezi nimi ( α , β , γ ). Objem jednotkové buňky lze vypočítat vyhodnocením trojného součinu a · ( b × c ) , kde a , b , a c jsou mřížkové vektory. Vlastnosti mřížových systémů jsou uvedeny níže:

Krystalová rodina	Mřížkový systém	Objem	Osové vzdálenosti (délky hran)	Axiální úhly	Odpovídající příklady
Triclinic		${\ Displaystyle abc {\ sqrt {1- \ cos ^{2} \ alpha -\ cos ^{2} \ beta -\ cos ^{2} \ gamma +2 \ cos \ alpha \ cos \ beta \ cos \ gamma }}}$	(Všechny zbývající případy)		K ₂ Cr ₂ O ₇ , CuSO ₄ · 5H ₂ O , H ₃ BO ₃
Monoklinika		${\ Displaystyle abc \, \ sin \ beta}$	a ≠ c	α = γ = 90 °, β ≠ 90 °	Monoklinická síra , Na ₂ SO ₄ · 10H ₂ O , PbCrO ₃
Orthorhombic		${\ displaystyle abc}$	a ≠ b ≠ c	α = β = γ = 90 °	Kosočtverečná síra , KNO ₃ , BaSO ₄
Tetragonální		${\ displaystyle a^{2} c}$	a = b ≠ c	α = β = γ = 90 °	Bílý cín , SnO ₂ , TiO ₂ , CaSO ₄
Šestihranný	Kosočtverečný	${\ Displaystyle a ^{3} {\ sqrt {1-3 \ cos ^{2} \ alpha +2 \ cos ^{3} \ alpha}}}$	a = b = c	α = β = γ ≠ 90 °	Kalcit (CaCO ₃ ), rumělka (HgS)
Šestihranný	Šestihranný	${\ displaystyle {\ frac {\ sqrt {3}} {2}} \, a^{2} c}$	a = b	α = β = 90 °, γ = 120 °	Grafit , ZnO , CdS
Krychlový		${\ displaystyle a^{3}}$	a = b = c	α = β = γ = 90 °	NaCl , směs zinku , kov mědi , KCl , diamant , stříbro

Ve 4 rozměrech

Ve čtyřech rozměrech je 64 mříží Bravais. Z nich je 23 primitivních a 41 soustředěných. Deset mřížek Bravais se rozdělilo na enantiomorfní páry.

Viz také

Reference

Další čtení

Bravais, A. (1850). „Mémoire sur les systèmes formés par les points distributiones régulièrement sur un plan ou dans l'espace“ [Monografie o systémech tvořených body pravidelně rozmístěnými v rovině nebo v prostoru]. J. École Polytech . 19 : 1–128. (Anglicky: Memoir 1, Crystallographic Society of America, 1949.)
Hahn, Theo, ed. (2002). Mezinárodní tabulky pro krystalografii, svazek A: Symetrie vesmírných skupin . Mezinárodní tabulky pro krystalografii. A (5. vyd.). Berlín, New York: Springer-Verlag . doi : 10,1107/97809553602060000100 . ISBN 978-0-7923-6590-7.

externí odkazy

Katalog mřížek (Nebe a Sloane)
Smith, Walter Fox (2002). „The Bravais Lattices Song“ .

Languages

In other projects