DFT matice - DFT matrix

V aplikované matematice je DFT matice výrazem diskrétní Fourierovy transformace (DFT) jako transformační matice , kterou lze aplikovat na signál prostřednictvím násobení matice .

Definice

N -bodu DFT je vyjádřena jako násobek , kde je původní vstupní signál, je na N -by- N čtvercový DFT matice, a je DFT signálu. ${\ displaystyle X = Wx}$${\ displaystyle x}$${\ displaystyle W}$ ${\ displaystyle X}$

Transformační matici lze definovat jako nebo ekvivalentně: ${\ displaystyle W}$${\ displaystyle W = \ left ({\ frac {\ omega ^ {jk}} {\ sqrt {N}}} \ right) _ {j, k = 0, \ ldots, N-1}}$

${\ displaystyle W = {\ frac {1} {\ sqrt {N}}} {\ begin {bmatrix} 1 & 1 & 1 & 1 & \ cdots & 1 \\ 1 & \ omega & \ omega ^ {2} & \ omega ^ {3} & \ cdots & \ omega ^ {N-1} \\ 1 & \ omega ^ {2} & \ omega ^ {4} & \ omega ^ {6} & \ cdots & \ omega ^ {2 (N-1)} \\ 1 & \ omega ^ {3} & \ omega ^ {6} & \ omega ^ {9} & \ cdots & \ omega ^ {3 (N-1)} \\\ vdots & \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ 1 & \ omega ^ {N-1} & \ omega ^ {2 (N-1)} & \ omega ^ {3 (N-1)} & \ cdots & \ omega ^ {(N -1) (N-1)} \ end {bmatrix}}}$,

kde je primitivní N- tý kořen jednoty, ve kterém . Můžeme se vyhnout psaní velkých exponentů pro použití skutečnosti, že pro každého exponenta máme identitu Toto je Vandermondeova matice pro kořeny jednoty, až do normalizačního faktoru. Všimněte si, že normalizační faktor před sum ( ) a znaménko exponenta v ω jsou pouze konvence a liší se v některých postupech. Všechna následující diskuse platí bez ohledu na konvenci, s maximálně malými úpravami. Jediné, co je důležité, že dopředu a inverzní transformace mají opačné znaménko exponenty, a že produktem jejich normalizace faktorů být 1 / N . Díky této volbě je však výsledná matice DFT jednotná , což je za mnoha okolností výhodné. ${\ displaystyle \ omega = e ^ {- 2 \ pi i / N}}$${\ displaystyle i ^ {2} = - 1}$${\ displaystyle \ omega}$${\ displaystyle x}$${\ displaystyle \ omega ^ {x} = \ omega ^ {x \ mod N}.}$${\ displaystyle 1 / {\ sqrt {N}}}$${\ displaystyle 1 / {\ sqrt {N}}}$

Algoritmy rychlé Fourierovy transformace využívají symetrie matice ke zkrácení doby vynásobení vektoru touto maticí z obvyklého . Podobné techniky lze použít pro násobení maticemi, jako je Hadamardova matice a Walshova matice . ${\ displaystyle O (N ^ {2})}$

Příklady

Dvoubodový

Dvoubodový DFT je jednoduchý případ, kdy první položka je DC (součet) a druhá položka je AC (rozdíl).

${\ displaystyle W = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 & 1 \\ 1 & -1 \ end {bmatrix}}}$

První řádek provádí součet a druhý řádek provádí rozdíl.

Faktorem je, aby byla transformace jednotná (viz níže). ${\ displaystyle 1 / {\ sqrt {2}}}$

Čtyřbodový

Čtyřbodová matice DFT ve směru hodinových ručiček je následující:

${\ displaystyle W = {\ frac {1} {\ sqrt {4}}} {\ begin {bmatrix} \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ { 0} \\\ omega ^ {0} & \ omega ^ {1} & \ omega ^ {2} & \ omega ^ {3} \\\ omega ^ {0} & \ omega ^ {2} & \ omega ^ {4} & \ omega ^ {6} \\\ omega ^ {0} & \ omega ^ {3} & \ omega ^ {6} & \ omega ^ {9} \\\ end {bmatrix}} = {\ frac {1} {\ sqrt {4}}} {\ begin {bmatrix} 1 & 1 & 1 & 1 \\ 1 & -i & -1 & i \\ 1 & -1 & 1 & -1 \\ 1 & i & -1 & -i \ end {bmatrix}}}$

kde . ${\ displaystyle \ omega = e ^ {- {\ frac {2 \ pi i} {4}}} = - i}$

Osmibodový

První netriviální celočíselná síla dvou případů je pro osm bodů:

${\ displaystyle W = {\ frac {1} {\ sqrt {8}}} {\ begin {bmatrix} \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ { 0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} & \ omega ^ {0} \\\ omega ^ {0} & \ omega ^ {1} & \ omega ^ { 2} & \ omega ^ {3} & \ omega ^ {4} & \ omega ^ {5} & \ omega ^ {6} & \ omega ^ {7} \\\ omega ^ {0} & \ omega ^ { 2} & \ omega ^ {4} & \ omega ^ {6} & \ omega ^ {8} & \ omega ^ {10} & \ omega ^ {12} & \ omega ^ {14} \\\ omega ^ { 0} & \ omega ^ {3} & \ omega ^ {6} & \ omega ^ {9} & \ omega ^ {12} & \ omega ^ {15} & \ omega ^ {18} & \ omega ^ {21 } \\\ omega ^ {0} & \ omega ^ {4} & \ omega ^ {8} & \ omega ^ {12} & \ omega ^ {16} & \ omega ^ {20} & \ omega ^ {24 } & \ omega ^ {28} \\\ omega ^ {0} & \ omega ^ {5} & \ omega ^ {10} & \ omega ^ {15} & \ omega ^ {20} & \ omega ^ {25 } & \ omega ^ {30} & \ omega ^ {35} \\\ omega ^ {0} & \ omega ^ {6} & \ omega ^ {12} & \ omega ^ {18} & \ omega ^ {24 } & \ omega ^ {30} & \ omega ^ {36} & \ omega ^ {42} \\\ omega ^ {0} & \ omega ^ {7} & \ omega ^ {14} & \ omega ^ {21 } & \ omega ^ {28} & \ omega ^ {35} & \ omega ^ {42} & \ omega ^ {49} \\\ end {bmatrix}} = {\ frac {1} {\ sqrt {8} }} {\ begin {bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & \ omega & -i & -i \ omega & -1 & - \ omega & i & i \ omega \\ 1 & -i & -1 & i & 1 & -i & -1 & i \\ 1 & -i \ omega & i & \ omega & -1 & i \ omega & -i & - \ omega \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & - \ omega & -i & i \ omega & -1 & \ omega & i & -i \ omega \\ 1 & i & -1 & -i & 1 & i & -1 & -i \\ 1 & i \ omega & i & - \ omega & -1 & -i \ omega & -i & \ omega \\\ konec {bmatrix}}}$

kde

${\ displaystyle \ omega = e ^ {- {\ frac {2 \ pi i} {8}}} = {\ frac {1} {\ sqrt {2}}} - {\ frac {i} {\ sqrt { 2}}}}$

(Všimněte si toho .) ${\ displaystyle \ omega ^ {8 + n} = \ omega ^ {n}}$

Následující obrázek zobrazuje DFT jako násobení matice, přičemž prvky matice jsou znázorněny vzorky komplexních exponenciálů:

Skutečná část (kosinová vlna) je označena plnou čarou a imaginární část (sinusová vlna) přerušovanou čarou.

Horní řádek jsou všechny (měřítko pro jednotnost), takže "měří" stejnosměrnou složku ve vstupním signálu. V dalším řádku je osm vzorků negativního jednoho cyklu komplexního exponenciálu, tj. Signálu s frakční frekvencí −1/8, takže „měří“, kolik „síly“ existuje při frakční frekvenci +1/8 v signál. Připomeňme, že odpovídající filtr porovnává signál s časově obrácenou verzí všeho, co hledáme, takže když hledáme fracfreq. 1/8 srovnáváme s fracfreq. −1/8, proto má tento řádek zápornou frekvenci . Další řádek jsou záporné dva cykly komplexního exponenciálu, vzorkované na osmi místech, takže má zlomkovou frekvenci −1/4, a tak „měří“ rozsah, v jakém má signál zlomkovou frekvenci +1/4. ${\ displaystyle 1 / {\ sqrt {8}}}$

Následující text shrnuje, jak funguje 8bodový DFT, řádek po řádku, pokud jde o zlomkovou frekvenci:

• 0 měří, kolik DC je v signálu
• −1/8 měří, kolik signálu má zlomkovou frekvenci +1/8
• −1/4 měří, kolik signálu má zlomkovou frekvenci +1/4
• −3/8 měří, kolik signálu má zlomkovou frekvenci +3/8
• −1/2 měří, kolik signálu má zlomkovou frekvenci +1/2
• −5/8 měří, kolik signálu má zlomkovou frekvenci +5/8
• −3/4 měří, kolik signálu má zlomkovou frekvenci +3/4
• −7/8 měří, kolik signálu má zlomkovou frekvenci +7/8

Ekvivalentně lze říci, že poslední řádek má zlomkovou frekvenci +1/8, a tak měří, kolik signálu má zlomkovou frekvenci -1/8. Tímto způsobem by se dalo říci, že horní řádky matice „měří“ kladný frekvenční obsah v signálu a spodní řádky měří zápornou frekvenční složku v signálu.

Jednotná transformace

DFT je (nebo může být vhodnou volbou škálování) jednotková transformace, tj. Transformace, která šetří energii. Vhodná volba škálování pro dosažení jednoty je taková, že energie ve fyzické doméně bude stejná jako energie ve Fourierově doméně, tj. K uspokojení Parsevalovy věty . (Pro výpočetní pohodlí se běžně používají i jiné než unitární škálování ; např. Věta o konvoluci má o něco jednodušší formu s škálováním zobrazeným v diskrétním článku Fourierovy transformace .) ${\ displaystyle 1 / {\ sqrt {N}}}$

Další vlastnosti

Další vlastnosti matice DFT, včetně jejích vlastních čísel, připojení k konvolucím, aplikacím atd., Najdete v článku o diskrétní Fourierově transformaci .

Omezující případ: operátor Fourier

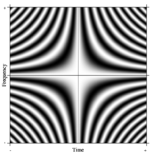
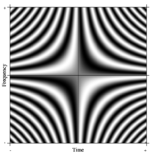
Pojem Fourierovy transformace je snadno zobecnitelný . Jedno takové formální zevšeobecnění N- bodu DFT si lze představit tak, že N je libovolně velké. V limitu přísný matematický aparát zachází s takovými lineárními operátory jako s takzvanými integrálními transformacemi . V tomto případě, pokud vytvoříme velmi velkou matici se složitými exponenciály v řádcích (tj. Kosinové reálné části a sinusové imaginární části), a zvětšíme rozlišení bez vazby, přiblížíme se k jádru Fredholmovy integrální rovnice 2. druhu, jmenovitě Fourierův operátor, který definuje spojitou Fourierovu transformaci. Obdélníková část tohoto spojitého Fourierova operátoru může být zobrazena jako obrázek, analogický s maticí DFT, jak je znázorněno vpravo, kde hodnota pixelu ve stupních šedi označuje číselnou veličinu.

Viz také

• Vícedimenzionální transformace
• Hodinové a posuvné matice

Reference

• Příručka Transformace a komprese dat od PC Yipa, K. Ramamohana Raa - viz kapitola 2, kde je popsáno zpracování DFT založené převážně na matici DFT

externí odkazy

• Fourierův operátor a decimace v čase (DIT)