Deltahedron - Deltahedron

Největší přísně konvexní deltahedron je pravidelný icosahedron

Jedná se o zkrácený čtyřstěn s šestiúhelníky rozdělenými do trojúhelníků. Toto číslo není striktně konvexní deltahedron, protože koplanární plochy nejsou v definici povoleny.

V geometrii je deltahedron ( množné číslo deltahedra ) mnohostěn, jehož tváře jsou všechny rovnostranné trojúhelníky . Název je převzat z řecké velké delty (Δ), která má tvar rovnostranného trojúhelníku. Deltahedra je nekonečně mnoho, všechny mají sudý počet tváří lemmatu potřesení rukou . Z nich je pouze osm konvexních a má 4, 6, 8, 10, 12, 14, 16 a 20 tváří. Počet ploch, hran a vrcholů je uveden níže pro každou z osmi konvexních deltahedra.

Osm konvexní deltahedra

Existuje pouze osm striktně konvexních deltahedrů: tři jsou pravidelné mnohostěny a pět jsou Johnsonovy pevné látky .

Pravidelná deltahedra
obraz	název	Tváře	Hrany	Vrcholy	Konfigurace vrcholů	Skupina symetrie
	čtyřstěn	4	6	4	4 × 3 3	T d , [3,3]
	osmistěn	8	12	6	6 × 3 4	O h , [4,3]
	icosahedron	20	30	12	12 × 3 5	I h , [5,3]
Johnson deltahedra
obraz	název	Tváře	Hrany	Vrcholy	Konfigurace vrcholů	Skupina symetrie
	trojúhelníkový bipyramid	6	9	5	2 × 3 3 3 × 3 4	D 3h , [3,2]
	pětiúhelníkový bipyramid	10	15	7	5 × 3 4 2 × 3 5	D 5h , [5,2]
	urazit disphenoid	12	18	8	4 × 3 4 4 × 3 5	D 2d , [2,2]
	trojúhelníkový trojúhelníkový hranol	14	21	9	3 × 3 4 6 × 3 5	D 3h , [3,2]
	gyroelongovaný čtvercový bipyramid	16	24	10	2 × 3 4 8 × 3 5	D 4d , [4,2]

V deltahedronu se 6 tvářemi mají některé vrcholy stupeň 3 a určitý stupeň 4. V deltahedře s 10, 12, 14 a 16 tvářemi mají některé vrcholy stupeň 4 a určitý stupeň 5. Těchto pět nepravidelných deltahedra patří třída Johnsonových těles : konvexní mnohostěn s pravidelnými mnohoúhelníky pro tváře.

Deltahedra si zachovává svůj tvar, i když se okraje mohou volně otáčet kolem svých vrcholů, takže úhly mezi hranami jsou plynulé. Ne všechny mnohostěny mají tuto vlastnost: například pokud uvolníte některé úhly krychle , může být krychle deformována do pravoúhlého hranolového hranolu .

Neexistuje žádný konvexní deltahedron s 18 tvářemi. Icosahedron se staženým okrajem však uvádí příklad oktadekedru, který může být buď konvexní s 18 nepravidelnými trojúhelníkovými plochami, nebo vyroben s rovnostrannými trojúhelníky, které obsahují dvě koplanární sady tří trojúhelníků.

Nekriticky konvexní případy

There are infinitely many cases with coplanar triangles, allowing for sections of the infinite triangular tilings. If the sets of coplanar triangles are considered a single face, a smaller set of faces, edges, and vertices can be counted. The coplanar triangular faces can be merged into rhombic, trapezoidal, hexagonal, or other equilateral polygon faces. Each face must be a convex polyiamond such as , , , , , , and , ...

Mezi menší příklady patří:

Coplanar deltahedra

obraz	název	Tváře	Hrany	Vrcholy	Konfigurace vrcholů	Skupina symetrie
	Augmented octahedron Augmentation 1 tet + 1 oct	10	15	7	1 × 3 3 3 × 3 4 3 × 3 5 0 × 3 6	C 3v , [3]
		4 3	12
	Trigonální lichoběžník Augmentace 2 tety + 1 okt	12	18	8	2 × 3 3 0 × 3 4 6 × 3 5 0 × 3 6	C 3v , [3]
		6	12
	Zvětšení 2 tets + 1 oct	12	18	8	2 × 3 3 1 × 3 4 4 × 3 5 1 × 3 6	C 2v , [2]
		2 2 2	11	7
	Zvětšení trojúhelníkového frustu 3 tety + 1 okt	14	21	9	3 × 3 3 0 × 3 4 3 × 3 5 3 × 3 6	C 3v , [3]
		1 3 1	9	6
	Prodloužené osmistěnové augmentace 2 tety + 2 oct	16	24	10	0 × 3 3 4 × 3 4 4 × 3 5 2 × 3 6	D 2h , [2,2]
		4 4	12	6
	Zvětšení čtyřstěnu 4 tety + 1 okt	16	24	10	4 × 3 3 0 × 3 4 0 × 3 5 6 × 3 6	T d , [3,3]
		4	6	4
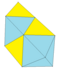
	Zvětšení 3 tety + 2 oct	18	27	11	1 × 3 3 2 × 3 4 5 × 3 5 3 × 3 6	D 2h , [2,2]
		2 1 2 2	14	9
	Hranatý smršťovací icosahedron	18	27	11	0 × 3 3 2 × 3 4 8 × 3 5 1 × 3 6	C 2v , [2]
		12 2	22	10
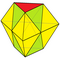
	Trojúhelníkový bifrustum Augmentace 6 TETS + 2 ZZÚ	20	30	12	0 × 3 3 3 × 3 4 6 × 3 5 3 × 3 6	D 3h , [3,2]
		2 6	15	9
	trojúhelníková kupole Zvětšení 4 tety + 3 oct	22	33	13	0 × 3 3 3 × 3 4 6 × 3 5 4 × 3 6	C 3v , [3]
		3 3 1 1	15	9
	Trojúhelníkové bipyramidové augmentace 8 tets + 2 oct	24	36	14	2 × 3 3 3 × 3 4 0 × 3 5 9 × 3 6	D 3h , [3]
		6	9	5
	Šestihranný antiprism	24	36	14	0 × 3 3 0 × 3 4 12 × 3 5 2 × 3 6	D 6d , [12,2 + ]
		12 2	24	12
	Zkrácení čtyřstěnu Augmentace 6 tets + 4 oct	28	42	16	0 × 3 3 0 × 3 4 12 × 3 5 4 × 3 6	T d , [3,3]
		4 4	18	12
	Tetrakis cuboctahedron Octahedron Augmentation 8 tets + 6 octs	32	48	18	0 × 3 3 12 × 3 4 0 × 3 5 6 × 3 6	O h , [4,3]
		8	12	6

Nekonvexní formy

Existuje nekonečně mnoho nekonvexních forem.

Několik příkladů obličeje protínajících se deltahedra:

• Velký icosahedron - těleso Kepler -Poinsot s 20 protínajícími se trojúhelníky

  

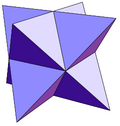
Další nekonvexní deltahedra lze generovat přidáním rovnostranných pyramid na plochy všech 5 pravidelných mnohostěnů:

triakis čtyřstěn	tetrakis šestihran	triakis octahedron ( stella octangula )	pentakis dodecahedron	triakis icosahedron
12 trojúhelníků	24 trojúhelníků		60 trojúhelníků

Mezi další augmentace čtyřstěnu patří:

Příklady: Augmented tetrahedra

8 trojúhelníků	10 trojúhelníků	12 trojúhelníků

Také přidáním obrácených pyramid na tváře:

• Vytěžený dvanáctistěn

Vytěžený dvanáctistěn	Toroidní deltahedron
60 trojúhelníků	48 trojúhelníků

Viz také

• Simplicial polytop - polytopes with all simplex facets

Reference

Další čtení

• Rausenberger, O. (1915), „Konvexe pseudoreguläre Polyeder“, Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht , 46 : 135–142.
• Cundy, H. Martyn (prosinec 1952), „Deltahedra“, Mathematical Gazette , 36 : 263–266, doi : 10,2307/3608204 , JSTOR  3608204.
• Cundy, H. Martyn ; Rollett, A. (1989), „3.11. Deltahedra“, Mathematical Models (3. vyd.), Stradbroke, England: Tarquin Pub., S. 142–144.
• Gardner, Martin (1992), Fractal Music, Hypercards a další: Mathematical Recreations from Scientific American , New York: WH Freeman, s. 40, 53 a 58-60.
• Pugh, Anthony (1976), Polyhedra: A visual approach , California: University of California Press Berkeley, ISBN 0-520-03056-7 s. 35–36

externí odkazy

• Weisstein, Eric W. , „Deltahedron“ , MathWorld
• Osm konvexní deltahedra
• Deltahedron
• Deltahedron