Diskrétní Fourierova transformace - Discrete Fourier transform

Vztah mezi (spojitou) Fourierovou transformací a diskrétní Fourierovou transformací. Levý sloupec: Spojitá funkce (nahoře) a její Fourierova transformace (dole). Středový levý sloupec: Periodické součty původní funkce (nahoře). Fourierova transformace (dole) je nula s výjimkou diskrétních bodů. Inverzní transformace je součtem sinusoidů zvaných Fourierova řada . Pravý středový sloupec: Původní funkce je diskretizována (vynásobena Diracovým hřebenem ) (nahoře). Jeho Fourierova transformace (dole) je periodickou sumací ( DTFT ) původní transformace. Pravý sloupec:DFT (dole) vypočítá diskrétní vzorky spojitého DTFT. Inverzní DFT (nahoře) je periodickým součtem původních vzorků. FFT algoritmus počítá jeden cyklus DFT a její inverze je jeden cyklus DFT inverzní.

Znázornění Fourierovy transformace (vlevo nahoře) a její periodické součty (DTFT) v dolním levém rohu. Spektrální sekvence v (a) vpravo nahoře a (b) vpravo dole se vypočítají z (a) jednoho cyklu periodického součtu s (t) a (b) jednoho cyklu periodického součtu sekvence s (nT) . Příslušné vzorce jsou (a) integrál Fourierovy řady a (b) součet DFT . Jeho podobnosti s původní transformací, S (f), a jeho relativní výpočetní snadnost jsou často motivací pro výpočet DFT sekvence.

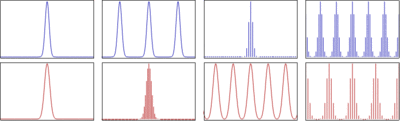
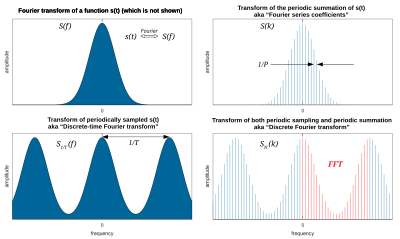
V matematiky je diskrétní Fourierova transformace ( DFT ) převede konečnou sekvenci rovnoměrně rozložených vzorků jednoho funkce do stejné délky posloupnosti rovnoměrně rozložených vzorků diskrétního Fourierova transformace (DTFT), který je s komplexními hodnotami funkce frekvence. Interval, ve kterém je vzorkován DTFT, je převrácenou délkou vstupní sekvence. Inverzní DFT je Fourierova řada , využívající vzorky DTFT jako koeficienty komplexních sinusoidů na odpovídajících frekvencích DTFT. Má stejné ukázkové hodnoty jako původní vstupní sekvence. DFT je proto údajně reprezentací původní vstupní sekvence ve frekvenční oblasti . Pokud původní sekvence překlenuje všechny nenulové hodnoty funkce, je její DTFT spojitý (a periodický) a DFT poskytuje diskrétní vzorky jednoho cyklu. Pokud je původní sekvence jeden cyklus periodické funkce, DFT poskytuje všechny nenulové hodnoty jednoho cyklu DTFT.

DFT je nejdůležitější diskrétní transformace , která se používá k provádění Fourierovy analýzy v mnoha praktických aplikacích. Při digitálním zpracování signálu je funkcí jakákoli veličina nebo signál, který se v čase mění, například tlak zvukové vlny , rádiový signál nebo denní měření teploty , vzorkované v určitém časovém intervalu (často definovaném funkcí okna ). Při zpracování obrazu mohou být vzorky hodnotami pixelů podél řádku nebo sloupce rastrového obrázku . DFT se také používá k efektivnímu řešení parciálních diferenciálních rovnic a k provádění dalších operací, jako jsou konvoluce nebo násobení velkých celých čísel.

Protože se zabývá konečným množstvím dat, může být implementován do počítačů pomocí numerických algoritmů nebo dokonce vyhrazeného hardwaru . Tyto implementace obvykle využívají efektivní rychlé algoritmy Fourierovy transformace (FFT); natolik, že pojmy „FFT“ a „DFT“ jsou často používány zaměnitelně. Před svým současným použitím mohl být inicializmus „FFT“ také použit pro nejednoznačný termín „ konečná Fourierova transformace “.

Definice

Diskrétní Fourierova transformace transformuje sekvencí z N komplexních čísel do jiné sekvence komplexních čísel, která je definována ${\ Displaystyle \ left \ {\ mathbf {x_ {n}} \ right \}: = x_ {0}, x_ {1}, \ ldots, x_ {N-1}}$${\ Displaystyle \ left \ {\ mathbf {X_ {k}} \ right \}: = X_ {0}, X_ {1}, \ ldots, X_ {N-1},}$

kde poslední výraz vyplývá z prvního Eulerovým vzorcem .

Transformace je někdy označena symbolem jako in nebo or . ${\ displaystyle {\ mathcal {F}}}$${\ displaystyle \ mathbf {X} = {\ mathcal {F}} \ left \ {\ mathbf {x} \ right \}}$${\ displaystyle {\ mathcal {F}} \ left (\ mathbf {x} \ right)}$${\ displaystyle {\ mathcal {F}} \ mathbf {x}}$

Motivace

Rovnici 1 lze také vyhodnotit mimo doménua tato rozšířená sekvence je- periodická . V souladu s tímse někdy používají ijiné sekvenceindexů, jako například(je-lisudé) a(je-liliché), což znamená prohození levé a pravé poloviny výsledku transformace. ${\ Displaystyle k \ v [0, N-1]}$${\ displaystyle N}$${\ displaystyle N}$${\ textstyle \ left [-{\ frac {N} {2}}, {\ frac {N} {2}}-1 \ right]}$${\ displaystyle N}$${\ textstyle \ left [-{\ frac {N-1} {2}}, {\ frac {N-1} {2}} \ right]}$${\ displaystyle N}$

Eq.1 lze interpretovat nebo odvodit různými způsoby, například:

Normalizační faktor násobící DFT a IDFT (zde 1 a ) a znaky exponentů jsou pouze konvence a v některých způsobech léčby se liší. Jediné požadavky těchto konvencí jsou, aby DFT a IDFT měly exponenty s opačným znaménkem a aby byl součin jejich normalizačních faktorů . Normalizace pro DFT i IDFT například činí transformace unitární. Diskrétní impuls, při n  = 0 a 0 jinak; se může transformovat na pro všechna k (použijte normalizační faktory 1 pro DFT a pro IDFT). DC signál, při k  = 0 a 0 jinak; se může inverzně transformovat na pro všechny (použití pro DFT a 1 pro IDFT), což je v souladu se zobrazením DC jako průměrného průměru signálu. ${\ textstyle {\ frac {1} {N}}}$${\ textstyle {\ frac {1} {N}}}$${\ textstyle {\ sqrt {\ frac {1} {N}}}}$${\ displaystyle x_ {n} = 1}$${\ displaystyle X_ {k} = 1}$${\ textstyle {\ frac {1} {N}}}$${\ displaystyle X_ {k} = 1}$${\ displaystyle x_ {n} = 1}$${\ displaystyle n}$${\ textstyle {\ frac {1} {N}}}$

Příklad

Znázornění matice DFT pro N = 8. Každý prvek je reprezentován obrazem jeho umístění v komplexní rovině ve vztahu k jednotkové kružnici.

Nechat a ${\ displaystyle N = 4}$

${\ Displaystyle \ mathbf {x} = {\ begin {pmatrix} x_ {0} \\ x_ {1} \\ x_ {2} \\ x_ {3} \ end {pmatrix}} = {\ begin {pmatrix} 1 \\ 2-i \\-i \\-1+2i \ end {pmatrix}}}$

Zde předvádíme, jak vypočítat DFT pomocí rovnice 1 : ${\ displaystyle \ mathbf {x}}$

${\ Displaystyle X_ {0} = e^{-i2 \ pi 0 \ cdot 0/4} \ cdot 1+e^{-i2 \ pi 0 \ cdot 1/4} \ cdot (2-i)+e^ {-i2 \ pi 0 \ cdot 2/4} \ cdot (-i)+e^{-i2 \ pi 0 \ cdot 3/4} \ cdot (-1+2i) = 2}$

${\ Displaystyle X_ {1} = e^{-i2 \ pi 1 \ cdot 0/4} \ cdot 1+e^{-i2 \ pi 1 \ cdot 1/4} \ cdot (2-i)+e^ {-i2 \ pi 1 \ cdot 2/4} \ cdot (-i)+e^{-i2 \ pi 1 \ cdot 3/4} \ cdot (-1+2i) =-2-2i}$

${\ Displaystyle X_ {2} = e^{-i2 \ pi 2 \ cdot 0/4} \ cdot 1+e^{-i2 \ pi 2 \ cdot 1/4} \ cdot (2-i)+e^ {-i2 \ pi 2 \ cdot 2/4} \ cdot (-i)+e^{-i2 \ pi 2 \ cdot 3/4} \ cdot (-1+2i) =-2i}$

${\ Displaystyle X_ {3} = e^{-i2 \ pi 3 \ cdot 0/4} \ cdot 1+e^{-i2 \ pi 3 \ cdot 1/4} \ cdot (2-i)+e^ {-i2 \ pi 3 \ cdot 2/4} \ cdot (-i)+e^{-i2 \ pi 3 \ cdot 3/4} \ cdot (-1+2i) = 4+4i}$

${\ Displaystyle \ mathbf {X} = {\ begin {pmatrix} X_ {0} \\ X_ {1} \\ X_ {2} \\ X_ {3} \ end {pmatrix}} = {\ begin {pmatrix} 2 \\-2-2i \\-2i \\ 4+4i \ end {pmatrix}}}$

Inverzní transformace

Diskrétní Fourierova transformace je invertibilní, lineární transformace

${\ Displaystyle {\ mathcal {F}} \ colon \ mathbb {C} ^{N} \ to \ mathbb {C} ^{N}}$

s označením množiny komplexních čísel . Jeho inverze je známá jako Inverse Discrete Fourier Transform (IDFT). Jinými slovy, pro všechny , An N rozměrný komplexní vektor má DFT a IDFT, které se dále rozměrný komplexní vektorů. ${\ displaystyle \ mathbb {C}}$${\ displaystyle N> 0}$${\ displaystyle N}$

Inverzní transformace je dána vztahem:

Vlastnosti

Linearita

DFT je lineární transformace, tj. Pokud a pak pro všechna komplexní čísla : ${\ displaystyle {\ mathcal {F}} (\ {x_ {n} \}) _ {k} = X_ {k}}$${\ displaystyle {\ mathcal {F}} (\ {y_ {n} \}) _ {k} = Y_ {k}}$${\ displaystyle a, b}$

${\ displaystyle {\ mathcal {F}} (\ {ax_ {n}+by_ {n} \}) _ {k} = aX_ {k}+bY_ {k}}$

Obrácení času a frekvence

Obrácení čas (tj nahrazení o ) v odpovídá zpětných frekvenci (tj o ). Matematicky, pokud představuje vektor x, pak ${\ displaystyle n}$${\ displaystyle Nn}$${\ displaystyle x_ {n}}$${\ displaystyle k}$${\ displaystyle Nk}$${\ displaystyle \ {x_ {n} \}}$

-li ${\ displaystyle {\ mathcal {F}} (\ {x_ {n} \}) _ {k} = X_ {k}}$

pak ${\ displaystyle {\ mathcal {F}} (\ {x_ {Nn} \}) _ {k} = X_ {Nk}}$

Konjugace v čase

Pokud ano . ${\ displaystyle {\ mathcal {F}} (\ {x_ {n} \}) _ {k} = X_ {k}}$${\ displaystyle {\ mathcal {F}} (\ {x_ {n}^{*} \}) _ {k} = X_ {Nk}^{*}}$

Skutečná a imaginární část

Tato tabulka ukazuje některé matematické operace v časové oblasti a odpovídající efekty na její DFT ve frekvenční oblasti. ${\ displaystyle x_ {n}}$${\ displaystyle X_ {k}}$

Vlastnictví	Časová doména ${\ displaystyle x_ {n}}$	Frekvenční doména ${\ displaystyle X_ {k}}$
Skutečná část v čase	${\ displaystyle \ Re {\ left (x_ {n} \ right)}}$	${\ displaystyle {\ frac {1} {2}} \ left (X_ {k}+X_ {Nk}^{*} \ right)}$
Imaginární část v čase	${\ displaystyle \ Im {\ left (x_ {n} \ right)}}$	${\ displaystyle {\ frac {1} {2i}} \ left (X_ {k} -X_ {Nk}^{*} \ right)}$
Skutečný podíl na frekvenci	${\ displaystyle {\ frac {1} {2}} \ left (x_ {n}+x_ {Nn}^{*} \ right)}$	${\ displaystyle \ Re {\ left (X_ {k} \ right)}}$
Imaginární část frekvence	${\ displaystyle {\ frac {1} {2i}} \ left (x_ {n} -x_ {Nn}^{*} \ right)}$	${\ displaystyle \ Im {\ left (X_ {k} \ right)}}$

Ortogonalita

Vektory tvoří ortogonální základ nad množinou N -rozměrných komplexních vektorů: ${\ Displaystyle u_ {k} = \ left [\ left.e^{{\ frac {i2 \ pi} {N}} kn} \; \ right | \; n = 0,1, \ ldots, N-1 \ right]^{\ ​​mathsf {T}}}$

${\ Displaystyle u_ {k}^{\ mathsf {T}} u_ {k '}^{*} = \ sum _ {n = 0}^{N-1} \ left (e^{{\ frac {i2 \ pi} {N}} kn} \ right) \ left (e^{{\ frac {i2 \ pi} {N}} (-k ') n} \ right) = \ sum _ {n = 0}^ {N-1} e^{{\ frac {i2 \ pi} {N}} (k-k ') n} = N ~ \ delta _ {kk'}}$

kde je Kroneckerova delta . (V posledním kroku je součet triviální, pokud , kde je 1 + 1 + ⋯ = N , a jinak jde o geometrickou řadu, kterou lze explicitně sečíst za účelem získání nuly.) Tuto podmínku ortogonality lze použít k odvození vzorce pro IDFT z definice DFT a je ekvivalentní níže uvedené vlastnosti unitarity. ${\ Displaystyle \ delta _ {kk '}}$${\ displaystyle k = k '}$

Plancherelova věta a Parsevalova věta

Pokud a jsou DFTs a potom, pak Parsevalova věta uvádí: ${\ displaystyle X_ {k}}$${\ displaystyle Y_ {k}}$${\ displaystyle x_ {n}}$${\ displaystyle y_ {n}}$

${\ Displaystyle \ sum _ {n = 0}^{N-1} x_ {n} y_ {n}^{*} = {\ frac {1} {N}} \ sum _ {k = 0}^{ N-1} X_ {k} Y_ {k}^{*}}$

kde hvězda označuje komplexní konjugaci . Plancherelova věta je speciální případ pastorální věty a uvádí:

${\ Displaystyle \ sum _ {n = 0}^{N-1} | x_ {n} |^{2} = {\ frac {1} {N}} \ sum _ {k = 0}^{N- 1} | X_ {k} |^{2}.}$

Tyto věty jsou také ekvivalentní níže uvedené unitární podmínce.

Periodicita

Periodicitu lze ukázat přímo z definice:

${\ Displaystyle X_ {k+N} \ \ triangleq \ \ sum _ {n = 0}^{N-1} x_ {n} e^{-{\ frac {i2 \ pi} {N}} (k+ N) n} = \ sum _ {n = 0}^{N-1} x_ {n} e^{-{\ frac {i2 \ pi} {N}} kn} \ underbrace {e^{-i2 \ pi n}} _ {1} = \ součet _ {n = 0}^{N-1} x_ {n} e^{-{\ frac {i2 \ pi} {N}} kn} = X_ {k} .}$

Podobně lze ukázat, že vzorec IDFT vede k periodickému prodloužení.

Shiftova věta

Vynásobením o lineární fáze pro některé celé číslo m odpovídá kruhového posunu výstupu : je nahrazen , kde je index interpretován modulo N (tj periodicky). Podobně kruhový posun vstupu odpovídá vynásobení výstupu lineární fází. Matematicky, pokud představuje vektor x, pak ${\ displaystyle x_ {n}}$ ${\ Displaystyle e^{{\ frac {i2 \ pi (n-1)} {N}} m}}$${\ displaystyle X_ {k}}$${\ displaystyle X_ {k}}$${\ displaystyle X_ {km}}$ ${\ displaystyle x_ {n}}$${\ displaystyle X_ {k}}$${\ displaystyle \ {x_ {n} \}}$

-li ${\ displaystyle {\ mathcal {F}} (\ {x_ {n} \}) _ {k} = X_ {k}}$

pak ${\ Displaystyle {\ mathcal {F}} \ left (\ left \ {x_ {n} \ cdot e^{{\ frac {i2 \ pi} {N}} nm} \ right \} \ right) _ {k } = X_ {km}}$

a ${\ Displaystyle {\ mathcal {F}} \ left (\ left \ {x_ {nm} \ right \} \ right) _ {k} = X_ {k} \ cdot e^{-{\ frac {i2 \ pi } {N}} km}}$

Věta o kruhové konvoluci a věta o vzájemné korelaci

Konvoluce věta pro diskrétního Fourierova transformace (DTFT), ukazuje, že konvoluce dvou sekvencí je možno získat inverzní transformace produktu z jednotlivých transformací. K významnému zjednodušení dochází, když je jedna ze sekvencí N-periodická, zde označená proto, že je nenulová pouze na diskrétních frekvencích (viz DTFT § Periodická data ), a tedy i její součin se spojitou funkcí,   která vede ke značnému zjednodušení inverzní transformace. ${\ displaystyle y _ {_ {N}},}$${\ displaystyle \ scriptstyle {\ text {DTFT}} \ displaystyle \ {y _ {_ {N}} \}}$${\ displaystyle \ scriptstyle {\ text {DTFT}} \ displaystyle \ {x \}.}$

${\ displaystyle x*y _ {_ {N}} \ = \ \ scriptstyle {\ rm {DTFT}}^{-1} \ displaystyle \ left [\ scriptstyle {\ rm {DTFT}} \ displaystyle \ {x \} \ cdot \ scriptstyle {\ rm {DTFT}} \ displaystyle \ {y _ {_ {N}} \} \ right] \ = \ \ scriptstyle {\ rm {DFT}}^{-1} \ displaystyle \ left [\ scriptstyle {\ rm {DFT}} \ displaystyle \ {x _ {_ {N}} \} \ cdot \ scriptstyle {\ rm {DFT}} \ displaystyle \ {y _ {_ {N}} \} \ right],}$

kde je periodická součet o sekvenci :${\ displaystyle x _ {_ {N}}}$${\ displaystyle x}$ ${\ Displaystyle (x _ {_ {N}}) _ {n} \ \ triangleq \ sum _ {m =-\ infty}^{\ infty} x _ {(n-mN)}.}$

Obvykle jsou nad doménou převzaty souhrny DFT a inverzní DFT . Definování těchto DFT jako a výsledkem je :${\ displaystyle [0, N-1]}$${\ displaystyle X}$${\ displaystyle Y}$

${\ Displaystyle (x*y _ {_ {N}}) _ {n} \ triangleq \ sum _ {\ ell =-\ infty}^{\ infty} x _ {\ ell} \ cdot (y _ {_ {N} }) _ {n- \ ell} = \ underbrace {{\ mathcal {F}}^{-1}} _ {\ rm {DFT^{-1}}} \ left \ {X \ cdot Y \ right \ } _ {n}.}$

V praxi má sekvence obvykle délku N nebo méně a je periodickým rozšířením sekvence délky N , kterou lze také vyjádřit jako kruhovou funkci :${\ displaystyle x}$${\ displaystyle y _ {_ {N}}}$${\ displaystyle y}$

${\ Displaystyle (y _ {_ {N}}) _ {n} = \ sum _ {p =-\ infty}^{\ infty} y _ {(n-pN)} = y _ {(n \ operatorname {mod} N)}, \ quad n \ in \ mathbb {Z}.}$

Pak může být konvoluce zapsána jako :

což vede k interpretaci jako kruhové konvoluce a často se používá k efektivnímu výpočtu jejich lineární konvoluce. (viz Kruhová konvoluce , algoritmy rychlé konvoluce a uložení s překrytím ) ${\ displaystyle x}$${\ Displaystyle y.}$

Podobně, vzájemná korelace z a je dán vztahem :${\ displaystyle x}$${\ displaystyle y _ {_ {N}}}$

${\ Displaystyle (x \ star y _ {_ {N}}) _ {n} \ triangleq \ sum _ {\ ell =-\ infty}^{\ infty} x _ {\ ell}^{*} \ cdot (y_ {_ {N}}) _ {n+\ ell} = {\ mathcal {F}}^{-1} \ left \ {X^{*} \ cdot Y \ right \} _ {n}.}$

Dualita věty o konvoluci

Lze také ukázat, že :

${\ Displaystyle {\ mathcal {F}} \ left \ {\ mathbf {x \ cdot y} \ right \} _ {k} \ \ triangleq \ sum _ {n = 0}^{N-1} x_ {n } \ cdot y_ {n} \ cdot e^{-i {\ frac {2 \ pi} {N}} kn}}$

${\ displaystyle = {\ frac {1} {N}} (\ mathbf {X*Y_ {N}}) _ {k},}$což je kruhová konvoluce a .${\ displaystyle \ mathbf {X}}$${\ displaystyle \ mathbf {Y}}$

Trigonometrický interpolační polynom

Trigonometrické interpolace polynom

${\ Displaystyle p (t) = {\ begin {cases} {\ frac {1} {N}} \ left [X_ {0}+X_ {1} e^{i2 \ pi t}+\ cdots+X_ { N/2-1} e^{i2 \ pi (N/2-1) t}+X_ {N/2} \ cos (N \ pi t)+X_ {N/2+1} e^{-i2 \ pi (N/2-1) t} +\ cdots +X_ {N-1} e^{-i2 \ pi t} \ right] & N {\ text {even}} \\ {\ frac {1} { N}} \ left [X_ {0}+X_ {1} e^{i2 \ pi t}+\ cdots+X _ {(N-1)/2} e^{i \ pi (N-1) t} +X _ {(N+1)/2} e^{-i \ pi (N-1) t}+\ cdots+X_ {N-1} e^{-i2 \ pi t} \ right] & N {\ text {odd}} \ end {cases}}}$

kde koeficienty X _k jsou dány DFT x _n výše, splňuje vlastnost interpolace pro . ${\ Displaystyle p (n/N) = x_ {n}}$${\ Displaystyle n = 0, \ ldots, N-1}$

U sudého N si všimněte, že se komponentou Nyquist zachází speciálně. ${\ textstyle {\ frac {X_ {N/2}} {N}} \ cos (N \ pi t)}$

Tato interpolace není ojedinělá : aliasing znamená, že by bylo možné přidat N ke kterékoli z komplexně sinusových frekvencí (např. Změna na ), aniž by došlo ke změně vlastnosti interpolace, ale mezi body by byly poskytnuty různé hodnoty . Výše uvedená volba je však typická, protože má dvě užitečné vlastnosti. Nejprve se skládá ze sinusoidů, jejichž frekvence mají nejmenší možné velikosti: interpolace je pásmová . Za druhé, pokud jsou reálná čísla, pak je také reálná. ${\ displaystyle e^{-it}}$${\ Displaystyle e^{i (N-1) t}}$${\ displaystyle x_ {n}}$${\ displaystyle x_ {n}}$${\ displaystyle p (t)}$

Naproti tomu nejzjevnějším trigonometrickým interpolačním polynomem je ten, ve kterém se frekvence pohybují od 0 do (místo zhruba do výše), podobně jako inverzní vzorec DFT. Tato interpolace však není minimalizovat sklon, a nikoli obecně reálná doopravdy ; jeho použití je častou chybou. ${\ displaystyle N-1}$${\ displaystyle -N/2}$${\ displaystyle +N/2}$${\ displaystyle x_ {n}}$

Unitární DFT

Další způsob, jak se dívat na DFT je třeba poznamenat, že ve výše uvedené diskusi DFT může být vyjádřena jako DFT matrice , je vandermondova matice , zavedeného Sylvester v roce 1867,

${\ Displaystyle \ mathbf {F} = {\ begin {bmatrix} \ omega _ {N}^{0 \ cdot 0} & \ omega _ {N}^{0 \ cdot 1} & \ cdots & \ omega _ { N}^{0 \ cdot (N-1)} \\\ omega _ {N}^{1 \ cdot 0} & \ omega _ {N}^{1 \ cdot 1} & \ cdots & \ omega _ { N}^{1 \ cdot (N-1)} \\\ vdots & \ vdots & \ ddots & \ vdots \\\ omega _ {N}^{(N-1) \ cdot 0} & \ omega _ { N}^{(N-1) \ cdot 1} & \ cdots & \ omega _ {N}^{(N-1) \ cdot (N-1)} \\\ end {bmatrix}}}$

kde je primitivní N tý kořen jednoty . ${\ Displaystyle \ omega _ {N} = e^{-i2 \ pi /N}}$

Inverzní transformace je pak dána inverzí výše uvedené matice,

${\ Displaystyle \ mathbf {F} ^{-1} = {\ frac {1} {N}} \ mathbf {F} ^{*}}$

S jednotkovými normalizačními konstantami se DFT stává unitární transformací , definovanou unitární maticí: ${\ textstyle 1/{\ sqrt {N}}}$

${\ displaystyle {\ begin {aligned} \ mathbf {U} & = {\ frac {1} {\ sqrt {N}}} \ mathbf {F} \\\ mathbf {U} ^{-1} & = \ mathbf {U} ^{*} \\\ left | \ det (\ mathbf {U}) \ right | & = 1 \ end {aligned}}}$

kde je určující funkce. Determinant je součin vlastních čísel, která jsou vždy nebo jak je popsáno níže. Ve skutečném vektorovém prostoru si lze unitární transformaci představit jednoduše jako tuhou rotaci souřadného systému a všechny vlastnosti tuhé rotace lze nalézt v unitárním DFT. ${\ displaystyle \ det ()}$${\ Displaystyle \ pm 1}$${\ Displaystyle \ pm i}$

Ortogonalita DFT je nyní vyjádřena jako podmínka ortonormality (která vzniká v mnoha oblastech matematiky, jak je popsáno v kořeni jednoty ):

${\ Displaystyle \ sum _ {m = 0}^{N-1} U_ {km} U_ {mn}^{*} = \ delta _ {kn}}$

Pokud je X definováno jako unitární DFT vektoru x , pak

${\ Displaystyle X_ {k} = \ sum _ {n = 0}^{N-1} U_ {kn} x_ {n}}$

a Parsevalova věta je vyjádřena jako

${\ Displaystyle \ sum _ {n = 0}^{N-1} x_ {n} y_ {n}^{*} = \ sum _ {k = 0}^{N-1} X_ {k} Y_ { k}^{*}}$

Pokud pohlížíme na DFT pouze jako transformaci souřadnic, která jednoduše specifikuje složky vektoru v novém souřadném systému, pak výše uvedené je pouze tvrzení, že bodový součin dvou vektorů je zachován pod jednotnou transformací DFT. Pro zvláštní případ to znamená, že je zachována i délka vektoru - je to jen Plancherelova věta , ${\ displaystyle \ mathbf {x} = \ mathbf {y}}$

${\ Displaystyle \ sum _ {n = 0}^{N-1} | x_ {n} |^{2} = \ sum _ {k = 0}^{N-1} | X_ {k} |^{ 2}}$

Důsledkem věty o kruhové konvoluci je, že DFT matice F diagonalizuje jakoukoli cirkulační matici .

Vyjádření inverzního DFT ve smyslu DFT

Užitečnou vlastností DFT je, že inverzní DFT lze snadno vyjádřit pomocí (dopředného) DFT pomocí několika známých „triků“. (Například ve výpočtech je často vhodné implementovat pouze rychlou Fourierovu transformaci odpovídající jednomu směru transformace a poté získat druhý směr transformace z prvního.)

Nejprve můžeme vypočítat inverzní DFT obrácením všech vstupů kromě jednoho (Duhamel et al. , 1988):

${\ displaystyle {\ mathcal {F}}^{-1} (\ {x_ {n} \}) = {\ frac {1} {N}} {\ mathcal {F}} (\ {x_ {Nn} \})}$

(Jako obvykle jsou dolní indexy interpretovány modulo N ; tedy pro , máme .) ${\ displaystyle n = 0}$${\ displaystyle x_ {N-0} = x_ {0}}$

Za druhé, lze také spojit vstupy a výstupy:

${\ Displaystyle {\ mathcal {F}} ^{-1} (\ mathbf {x}) = {\ frac {1} {N}} {\ mathcal {F}} \ left (\ mathbf {x} ^{ *} \ vpravo)^{*}}$

Za třetí, varianta tohoto konjugačního triku, která je někdy výhodnější, protože nevyžaduje žádnou úpravu datových hodnot, zahrnuje výměnu skutečných a imaginárních částí (což lze provést na počítači jednoduše úpravou ukazatelů ). Definovat jako s jeho skutečné a imaginární části vyměnil, to znamená, že v případě, pak je . Ekvivalentně, rovná se . Pak ${\ textstyle \ operatorname {swap} (x_ {n})}$${\ displaystyle x_ {n}}$${\ displaystyle x_ {n} = a+bi}$${\ textstyle \ operatorname {swap} (x_ {n})}$${\ displaystyle b+ai}$${\ textstyle \ operatorname {swap} (x_ {n})}$${\ displaystyle ix_ {n}^{*}}$

${\ displaystyle {\ mathcal {F}}^{-1} (\ mathbf {x}) = {\ frac {1} {N}} \ operatorname {swap} ({\ mathcal {F}} (\ operatorname { swap} (\ mathbf {x})))}$

To znamená, že inverzní transformace je stejná jako dopředná transformace se skutečnými a imaginárními částmi vyměněnými za vstup i výstup, a to až do normalizace (Duhamel et al. , 1988).

Konjugační trik lze také použít k definování nové transformace, úzce související s DFT, která je nedovolená - to znamená, že je její vlastní inverzní. Zejména je jasně jeho vlastní inverzní: . Úzce související evolutorní transformace (faktorem ) je , protože faktory ruší 2. Pro skutečné vstupy není skutečnou součástí nikdo jiný než diskrétní Hartleyova transformace , která je také evolutorní. ${\ Displaystyle T (\ mathbf {x}) = {\ mathcal {F}} \ left (\ mathbf {x} ^{*} \ right)/{\ sqrt {N}}}$${\ Displaystyle T (T (\ mathbf {x})) = \ mathbf {x}}$${\ textstyle {\ frac {1+i} {\ sqrt {2}}}}$${\ Displaystyle H (\ mathbf {x}) = {\ mathcal {F}} \ left ((1+i) \ mathbf {x} ^{*} \ right)/{\ sqrt {2N}}}$${\ displaystyle (1+i)}$${\ Displaystyle H (H (\ mathbf {x}))}$${\ displaystyle \ mathbf {x}}$${\ displaystyle H (\ mathbf {x})}$

Vlastní čísla a vlastní vektory

Vlastní čísla matice DFT jsou jednoduchá a dobře známá, zatímco vlastní vektory jsou komplikovaná, nikoli jedinečná a jsou předmětem probíhajícího výzkumu.

Zvažte jednotnou formu definovanou výše pro DFT délky N , kde ${\ displaystyle \ mathbf {U}}$

${\ Displaystyle \ mathbf {U} _ {m, n} = {\ frac {1} {\ sqrt {N}}} \ omega _ {N}^{(m-1) (n-1)} = { \ frac {1} {\ sqrt {N}}} e^{-{\ frac {i2 \ pi} {N}} (m-1) (n-1)}.}$

Tato matice splňuje maticovou polynomickou rovnici:

${\ Displaystyle \ mathbf {U} ^{4} = \ mathbf {I}.}$

To lze vidět na výše uvedených inverzních vlastnostech: dvakrát operovat dává původní data v opačném pořadí, takže čtyřnásobná operace vrací původní data a je tedy maticí identity . To znamená, že vlastní čísla splňují rovnici: ${\ displaystyle \ mathbf {U}}$${\ displaystyle \ mathbf {U}}$${\ Displaystyle \ lambda}$

${\ Displaystyle \ lambda ^{4} = 1.}$

Vlastní čísla jsou tedy čtvrtými kořeny jednoty : je +1, −1, + i , nebo - i . ${\ displaystyle \ mathbf {U}}$${\ Displaystyle \ lambda}$

Protože pro tuto matici existují pouze čtyři odlišná vlastní čísla , mají určitou multiplicitu . Násobnost udává počet lineárně nezávislých vlastních vektorů odpovídajících každé vlastní hodnotě. (Existuje N nezávislých vlastních vektorů; unitární matice není nikdy vadná .) ${\ displaystyle N \ times N}$

Problém jejich mnohosti vyřešili McClellan a Parks (1972), ačkoli se později ukázalo, že byl ekvivalentní problému, který vyřešil Gauss (Dickinson a Steiglitz, 1982). Násobnost závisí na hodnotě N modulo 4 a je dána následující tabulkou:

Jinak řečeno, charakteristický polynom z IS: ${\ displaystyle \ mathbf {U}}$

${\ Displaystyle \ det (\ lambda I- \ mathbf {U}) = (\ lambda -1)^{\ left \ lfloor {\ tfrac {N +4} {4}} \ right \ rfloor} (\ lambda + 1)^{\ left \ lfloor {\ tfrac {N+2} {4}} \ right \ rfloor} (\ lambda+i)^{\ left \ lfloor {\ tfrac {N+1} {4}} \ vpravo \ rfloor} (\ lambda -i)^{\ left \ lfloor {\ tfrac {N -1} {4}} \ right \ rfloor}.}$

Není znám jednoduchý analytický vzorec pro obecné vlastní vektory. Vlastní čísla navíc nejsou jedinečná, protože jakákoli lineární kombinace vlastních vektorů pro stejné vlastní číslo je také vlastním vektorem pro toto vlastní číslo. Různí vědci navrhli různé možnosti vlastních vektorů, vybraných tak, aby uspokojovaly užitečné vlastnosti, jako je ortogonalita, a aby měly „jednoduché“ formy (např. McClellan a Parks, 1972; Dickinson a Steiglitz, 1982; Grünbaum, 1982; Atakishiyev a Wolf, 1997; Candan et al. , 2000; Hanna et al. , 2004; Gurevich a Hadani, 2008).

Jednoduchým přístupem je diskretizace vlastní funkce spojité Fourierovy transformace , z nichž nejznámější je Gaussova funkce . Protože periodická sumace funkce znamená diskretizaci jejího frekvenčního spektra a diskretizace znamená periodickou sumaci spektra, diskretizovaná a periodicky sečtená Gaussova funkce poskytuje vlastní vektor diskrétní transformace:

• ${\ Displaystyle F (m) = \ sum _ {k \ in \ mathbb {Z}} \ exp \ left (-{\ frac {\ pi \ cdot (m+N \ cdot k)^{2}} {N }}\že jo).}$

Výraz uzavřené formy pro řadu lze vyjádřit Jacobi theta funguje jako

• ${\ Displaystyle F (m) = {\ frac {1} {\ sqrt {N}}} \ vartheta _ {3} \ left ({\ frac {\ pi m} {N}}, \ exp \ left (- {\ frac {\ pi} {N}} \ right) \ right).}$

Byly nalezeny další dva jednoduché uzavřené analytické vlastní vektory pro speciální období DFT N (Kong, 2008):

Pro období DFT N = 2 L + 1 = 4 K + 1, kde K je celé číslo, následující je vlastní vektor DFT:

• ${\ Displaystyle F (m) = \ prod _ {s = K+1}^{L} \ left [\ cos \ left ({\ frac {2 \ pi} {N}} m \ right)-\ cos \ vlevo ({\ frac {2 \ pi} {N}} s \ right) \ right]}$

Pro období DFT N = 2 L = 4 K , kde K je celé číslo, je vlastní vektor DFT:

• ${\ Displaystyle F (m) = \ sin \ left ({\ frac {2 \ pi} {N}} m \ right) \ prod _ {s = K+1}^{L-1} \ left [\ cos \ left ({\ frac {2 \ pi} {N}} m \ right)-\ cos \ left ({\ frac {2 \ pi} {N}} s \ right) \ right]}$

Volba vlastních vektorů DFT matice je v posledních letech důležitá, aby bylo možné definovat diskrétní analog zlomkové Fourierovy transformace - DFT matici lze přenést na zlomkové mocniny umocněním vlastních čísel (např. Rubio a Santhanam, 2005). Pro spojitou Fourierovu transformaci jsou přirozenými ortogonálními vlastními funkcemi Hermitovy funkce , takže jako vlastní vektory DFT byly použity různé jejich diskrétní analogy, jako jsou Kravčukovy polynomy (Atakishiyev a Wolf, 1997). „Nejlepší“ volba vlastních vektorů k definování zlomkové diskrétní Fourierovy transformace však zůstává otevřenou otázkou.

Zásady nejistoty

Princip pravděpodobnostní neurčitosti

Pokud je náhodná proměnná X _k omezena

${\ Displaystyle \ sum _ {n = 0}^{N-1} | X_ {n} |^{2} = 1,}$

pak

${\ displaystyle P_ {n} = | X_ {n} |^{2}}$

může být považován za diskrétní pravděpodobnost hmotnostní funkci z n , s přidruženým pravděpodobnost hmotnostní funkce vytvořené z transformovaného proměnné,

${\ Displaystyle Q_ {m} = N | x_ {m} |^{2}.}$

Pro případ spojitých funkcí a to říká Heisenbergův princip neurčitosti${\ displaystyle P (x)}$${\ displaystyle Q (k)}$

${\ displaystyle D_ {0} (X) D_ {0} (x) \ geq {\ frac {1} {16 \ pi ^{2}}}}$

kde a jsou odchylky a respektive s rovností dosaženou v případě vhodně normalizovaného Gaussova rozdělení . Ačkoli mohou být odchylky pro DFT definovány analogicky, analogický princip nejistoty není užitečný, protože nejistota nebude invariantní vůči posunu. Massar a Spindel přesto zavedli smysluplný princip nejistoty. ${\ displaystyle D_ {0} (X)}$${\ displaystyle D_ {0} (x)}$${\ displaystyle | X |^{2}}$${\ displaystyle | x |^{2}}$

Hirschmanova entropická nejistota však bude mít užitečný analog pro případ DFT. Hirschmanův princip neurčitosti je vyjádřen shannonskou entropií obou pravděpodobnostních funkcí.

V diskrétním případě jsou Shannonovy entropie definovány jako

${\ Displaystyle H (X) =-\ sum _ {n = 0}^{N-1} P_ {n} \ ln P_ {n}}$

a

${\ Displaystyle H (x) =-\ sum _ {m = 0}^{N-1} Q_ {m} \ ln Q_ {m},}$

a princip entropické nejistoty se stává

${\ Displaystyle H (X)+H (x) \ geq \ ln (N).}$

Rovnost se získá pro rovné překladům a modulacím vhodně normalizovaného Kroneckerova hřebene období, kde je jakýkoli přesný celočíselný dělitel . Funkce pravděpodobnostní hmotnosti pak bude úměrná vhodně přeloženému Kroneckerovu hřebenu období . ${\ displaystyle P_ {n}}$${\ displaystyle A}$${\ displaystyle A}$${\ displaystyle N}$${\ displaystyle Q_ {m}}$${\ displaystyle B = N/A}$

Deterministický princip neurčitosti

Existuje také dobře známý princip deterministické neurčitosti, který využívá řídkost signálu (nebo počet nenulových koeficientů). Nechť a je počet nenulových prvků časové a frekvenční posloupnosti a . Pak, ${\ Displaystyle \ left \ | x \ right \ | _ {0}}$${\ Displaystyle \ left \ | X \ right \ | _ {0}}$${\ displaystyle x_ {0}, x_ {1}, \ ldots, x_ {N-1}}$${\ displaystyle X_ {0}, X_ {1}, \ ldots, X_ {N-1}}$

${\ Displaystyle N \ leq \ left \ | x \ right \ | _ {0} \ cdot \ left \ | X \ right \ | _ {0}.}$

Jako bezprostřední důsledek nerovnosti aritmetických a geometrických průměrů má také jeden . Ukázalo se, že oba principy nejistoty jsou těsné pro specificky zvolené sekvence „picket-plot“ (diskrétní impulzní vlaky) a nacházejí praktické využití pro aplikace pro obnovu signálu. ${\ Displaystyle 2 {\ sqrt {N}} \ leq \ left \ | x \ right \ | _ {0}+\ left \ | X \ right \ | _ {0}}$

DFT skutečných a čistě imaginárních signálů

• Pokud jsou reálná čísla , protože často jsou v praktických aplikacích, pak DFT je i symetrický :${\ displaystyle x_ {0}, \ ldots, x_ {N-1}}$${\ displaystyle X_ {0}, \ ldots, X_ {N-1}}$

${\ Displaystyle x_ {n} \ in \ mathbb {R} \ quad \ forall n \ in \ {0, \ ldots, N-1 \} \ implikuje X_ {k} = X _ {-k \ mod N}^{ *} \ quad \ forall k \ in \ {0, \ ldots, N-1 \}}$, kde označuje komplexní konjugaci .${\ displaystyle X^{*} \,}$

Z toho vyplývá, že pro sudé a mají skutečnou hodnotu a zbytek DFT je zcela specifikován pouze komplexními čísly. ${\ displaystyle N}$ ${\ displaystyle X_ {0}}$${\ displaystyle X_ {N/2}}$${\ Displaystyle N/2-1}$

• Pokud jsou čistě imaginární čísla, pak DFT je liché symetrický :${\ displaystyle x_ {0}, \ ldots, x_ {N-1}}$${\ displaystyle X_ {0}, \ ldots, X_ {N-1}}$

${\ Displaystyle x_ {n} \ in i \ mathbb {R} \ quad \ forall n \ in \ {0, \ ldots, N-1 \} \ implikuje X_ {k} =-X _ {-k \ mod N} ^{*} \ quad \ forall k \ in \ {0, \ ldots, N-1 \}}$, kde označuje komplexní konjugaci .${\ displaystyle X^{*} \,}$

Zobecněný DFT (posunutá a nelineární fáze)

Je možné posunout transformace vzorkování v čase a / nebo frekvenční doméně skutečnými posuny dobu a B , v uvedeném pořadí. Toto je někdy známé jako zobecněný DFT (nebo GDFT ), také nazývaný posunutý DFT nebo offsetový DFT , a má analogické vlastnosti s běžným DFT:

${\ Displaystyle X_ {k} = \ sum _ {n = 0}^{N-1} x_ {n} e^{-{\ frac {i2 \ pi} {N}} (k+b) (n+ a)} \ quad \ quad k = 0, \ dots, N-1.}$

Nejčastěji se používají posuny (polovina vzorku). Zatímco obyčejný DFT odpovídá periodickému signálu v časové i frekvenční oblasti, vytváří signál, který je ve frekvenční doméně ( ) antiodiodický a naopak . Konkrétní případ je tedy znám jako lichá časová lichá frekvence diskrétní Fourierova transformace (nebo O ² DFT). Takto posunuté transformace se nejčastěji používají pro symetrická data, pro reprezentaci různých hraničních symetrií a pro real-symetrická data odpovídají různým formám diskrétních kosinových a sinusových transformací. ${\ Displaystyle 1/2}$${\ displaystyle a = 1/2}$${\ displaystyle X_ {k+N} =-X_ {k}}$${\ Displaystyle b = 1/2}$${\ Displaystyle a = b = 1/2}$

Další zajímavou volbou je , která se nazývá centrovaný DFT (nebo CDFT ). Vycentrovaný DFT má užitečnou vlastnost, že když N je násobek čtyř, všechny čtyři vlastní hodnoty (viz výše) mají stejnou multiplicitu (Rubio a Santhanam, 2005) ${\ Displaystyle a = b =-(N-1)/2}$

Termín GDFT se také používá pro nelineární fázová rozšíření DFT. Metoda GDFT proto poskytuje zobecnění pro ortogonální blokové transformace s konstantní amplitudou včetně lineárních a nelineárních fázových typů. GDFT je rámec pro zlepšení vlastností časové a frekvenční oblasti tradičního DFT, např. Automatické/křížové korelace, přidáním správně navržené funkce tvarování fází (obecně nelineární) k původním funkcím lineární fáze (Akansu a Agirman-Tosun, 2010).

Na diskrétní Fourierovu transformaci lze pohlížet jako na speciální případ z-transformace , hodnocené na jednotkové kružnici v komplexní rovině; obecnější z-transformace odpovídají komplexním posunům a a b výše.

Multidimenzionální DFT

Běžný DFT transformuje jednorozměrnou sekvenci nebo pole, které je funkcí přesně jedné diskrétní proměnné n . Multidimenzionální DFT vícerozměrného pole, které je funkcí d diskrétních proměnných pro in, je definováno: ${\ displaystyle x_ {n}}$${\ Displaystyle x_ {n_ {1}, n_ {2}, \ tečky, n_ {d}}}$${\ Displaystyle n _ {\ ell} = 0,1, \ tečky, N _ {\ ell} -1}$${\ displaystyle \ ell}$${\ Displaystyle 1,2, \ tečky, d}$

${\ Displaystyle X_ {k_ {1}, k_ {2}, \ dots, k_ {d}} = \ sum _ {n_ {1} = 0}^{N_ {1} -1} \ left (\ omega _ {N_ {1}}^{~ k_ {1} n_ {1}} \ sum _ {n_ {2} = 0}^{N_ {2} -1} \ left (\ omega _ {N_ {2}} ^{~ k_ {2} n_ {2}} \ cdots \ sum _ {n_ {d} = 0}^{N_ {d} -1} \ omega _ {N_ {d}}^{~ k_ {d} n_ {d}} \ cdot x_ {n_ {1}, n_ {2}, \ dots, n_ {d}} \ right) \ right),}$

kde, jak je uvedeno výše, a odtud běží indexy výstupu d . Toto je kompaktněji vyjádřeno ve vektorovém zápisu, kde definujeme a jako d -rozměrné vektory indexů od 0 do , které definujeme jako : ${\ displaystyle \ omega _ {N _ {\ ell}} = \ exp (-i2 \ pi /N _ {\ ell})}$${\ Displaystyle k _ {\ ell} = 0,1, \ tečky, N _ {\ ell} -1}$${\ Displaystyle \ mathbf {n} = (n_ {1}, n_ {2}, \ dots, n_ {d})}$${\ Displaystyle \ mathbf {k} = (k_ {1}, k_ {2}, \ tečky, k_ {d})}$${\ Displaystyle \ mathbf {N} -1}$${\ Displaystyle \ mathbf {N} -1 = (N_ {1} -1, N_ {2} -1, \ dots, N_ {d} -1)}$

${\ Displaystyle X _ {\ mathbf {k}} = \ sum _ {\ mathbf {n} = \ mathbf {0}}^{\ mathbf {N} -1} e^{ -i2 \ pi \ mathbf {k} \ cdot (\ mathbf {n} /\ mathbf {N})} x _ {\ mathbf {n}} \ ,,}$

kde je dělení definováno tak, aby bylo provedeno po prvcích, a součet označuje sadu vnořených součtů výše. ${\ Displaystyle \ mathbf {n} /\ mathbf {N}}$${\ Displaystyle \ mathbf {n}/\ mathbf {N} = (n_ {1}/N_ {1}, \ tečky, n_ {d}/N_ {d})}$

Převrácená hodnota vícerozměrného DFT je, analogicky k jednorozměrnému případu, dána vztahem:

${\ Displaystyle x _ {\ mathbf {n}} = {\ frac {1} {\ prod _ {\ ell = 1}^{d} N _ {\ ell}}} \ sum _ {\ mathbf {k} = \ mathbf {0}}^{\ mathbf {N} -1} e^{i2 \ pi \ mathbf {n} \ cdot (\ mathbf {k} /\ mathbf {N})} X _ {\ mathbf {k}} \ ,.}$

Protože jednorozměrný DFT vyjadřuje vstup jako superpozici sinusoidů, multidimenzionální DFT vyjadřuje vstup jako superpozici rovinných vln nebo vícerozměrných sinusoidů. Směr oscilace v prostoru je . Amplitudy jsou . Tento rozklad má velký význam pro vše od digitálního zpracování obrazu (dvojrozměrného) po řešení parciálních diferenciálních rovnic . Roztok je rozdělen na rovinné vlny. ${\ displaystyle x_ {n}}$${\ Displaystyle \ mathbf {k} /\ mathbf {N}}$${\ displaystyle X _ {\ mathbf {k}}}$

Multidimenzionální DFT lze vypočítat složením sekvence jednorozměrných DFT podél každé dimenze. V dvojrozměrném případě se nejprve vypočítají nezávislé DFT řádků (tj. Podél ), aby vytvořily nové pole . Poté se vypočítají nezávislé DFT y podél sloupců (podél ) a vytvoří konečný výsledek . Alternativně lze nejprve vypočítat sloupce a poté řádky. Pořadí je nehmotné, protože vnořené součty nad dojížděním . ${\ displaystyle x_ {n_ {1}, n_ {2}}}$${\ displaystyle N_ {1}}$${\ displaystyle n_ {2}}$${\ displaystyle y_ {n_ {1}, k_ {2}}}$${\ displaystyle N_ {2}}$${\ displaystyle n_ {1}}$${\ displaystyle X_ {k_ {1}, k_ {2}}}$