Einstein solid - Einstein solid

Einstein pevná látka je model krystalická pevná látka, která obsahuje velký počet nezávislých trojrozměrný lineární harmonický oscilátor na stejné frekvenci. Předpoklad nezávislosti je v modelu Debye zmírněn .

Zatímco model poskytuje kvalitativní shodu s experimentálními daty, zejména pro vysokoteplotní limit, tyto oscilace jsou ve skutečnosti fonony nebo kolektivní režimy zahrnující mnoho atomů. Einstein si byl vědom, že získání frekvence skutečných oscilací by bylo obtížné, nicméně navrhl tuto teorii, protože to byla obzvláště jasná ukázka, že kvantová mechanika může vyřešit problém specifického tepla v klasické mechanice.

Historický dopad

Původní teorie navržená Einsteinem v roce 1907 má velký historický význam. Tepelná kapacita z pevných látek , jak předpokládá empirickým zákonem Dulong-Petit se požaduje klasické mechaniky , měrné teplo pevných látek by měla být nezávislá na teplotě. Ale experimenty při nízkých teplotách ukázaly, že tepelná kapacita se mění a na absolutní nulu jde k nule. Jak teplota stoupá, stoupá měrné teplo, dokud se při vysoké teplotě nepřiblíží předpovědi Dulong a Petit.

Použitím Planckova kvantizačního předpokladu Einsteinova teorie poprvé představovala pozorovaný experimentální trend. Spolu s fotoelektrickým efektem se to stalo jedním z nejdůležitějších důkazů o potřebě kvantizace. Einstein používal úrovně kvantově mechanického oscilátoru mnoho let před příchodem moderní kvantové mechaniky .

Tepelná kapacita

Pro termodynamický přístup lze tepelnou kapacitu odvodit pomocí různých statistických souborů . Všechna řešení jsou ekvivalentní na termodynamické hranici .

Mikrokanonický soubor

Tepelná kapacita Einsteinovy pevné látky jako funkce teploty. Experimentální hodnota 3 Nk se získá při vysokých teplotách.

Tepelná kapacita objektu při konstantním objemu V je definován prostřednictvím vnitřní energie U jako

{\ displaystyle C_ {V} = \ vlevo ({\ částečné U \ nad \ částečné T} \ pravé) _ {V}.}

${\ displaystyle T}$ , teplotu systému, lze zjistit z entropie

{\ displaystyle {1 \ přes T} = {\ částečné S \ přes \ částečné U}.}

Chcete-li najít entropii, zvažte pevnou látku vytvořenou z atomů, z nichž každý má 3 stupně volnosti. Existují tedy kvantové harmonické oscilátory (dále SHO pro „Simple Harmonic Oscillators“). ${\ displaystyle N}$ ${\ displaystyle 3N}$

{\ displaystyle N ^ {\ prime} = 3N}

Možné energie SHO jsou dány

{\ displaystyle E_ {n} = \ hbar \ omega \ left (n + {1 \ over 2} \ right)}

nebo jinými slovy, energetické úrovně jsou rovnoměrně rozmístěny a lze definovat kvantum energie

{\ displaystyle \ varepsilon = \ hbar \ omega}

což je nejmenší a jediné množství, o které se zvyšuje energie SHO. Dále musíme vypočítat multiplicitu systému. To znamená, že spočítejte počet způsobů, jak rozdělit kvantum energie mezi SHO. Tento úkol se stává jednodušším, pokud si někdo pomyslí na distribuci oblázků přes krabice ${\ displaystyle q}$ ${\ displaystyle N ^ {\ prime}}$ ${\ displaystyle q}$ ${\ displaystyle N ^ {\ prime}}$

nebo oddělování hromádek oblázků s oddíly ${\ displaystyle N ^ {\ prime} -1}$

nebo uspořádání oblázků a příček ${\ displaystyle q}$ ${\ displaystyle N ^ {\ prime} -1}$

Poslední obrázek je nejdůležitější. Počet uspořádání objektů je . Počet možných uspořádání oblázků a oddílů je tedy . Pokud by se však oddíl č. 3 a oddíl č. 5 obchodoval, nikdo by si toho nevšiml. Stejný argument platí pro kvantá. K získání počtu možných rozlišitelných uspořádání je třeba vydělit celkový počet uspořádání počtem nerozlišitelných uspořádání. Existují stejná uspořádání kvant a stejná uspořádání oddílů. Násobnost systému je tedy dána vztahem ${\ displaystyle n}$ ${\ displaystyle n!}$ ${\ displaystyle q}$ ${\ displaystyle N ^ {\ prime} -1}$ ${\ displaystyle \ left (q + N ^ {\ prime} -1 \ right)!}$ ${\ displaystyle q!}$ ${\ displaystyle (N ^ {\ prime} -1)!}$

{\ displaystyle \ Omega = {\ vlevo (q + N ^ {\ prime} -1 \ vpravo)! \ přes q! (N ^ {\ prime} -1)!}}

což je, jak již bylo zmíněno dříve, počet způsobů, jak vložit kvantum energie do oscilátorů. Entropie systému má formu ${\ displaystyle q}$ ${\ displaystyle N ^ {\ prime}}$

{\ Displaystyle S / k = \ ln \ Omega = \ ln {\ doleva (q + N ^ {\ prime} -1 \ doprava)! \ over q! (N ^ {\ prime} -1)!}.}

${\ displaystyle N ^ {\ prime}}$ je obrovské číslo - odečtení jednoho od něj nemá žádný celkový účinek:

{\ displaystyle S / k \ přibližně \ ln {\ doleva (q + N ^ {\ prime} \ doprava)! \ přes q! N ^ {\ prime}!}}

Pomocí Stirlingovy aproximace lze entropii zjednodušit:

{\ Displaystyle S / k \ přibližně \ vlevo (q + N ^ {\ prime} \ vpravo) \ ln \ vlevo (q + N ^ {\ prime} \ vpravo) -N ^ {\ prime} \ ln N ^ { \ prime} -q \ ln q.}

Celková energie pevné látky je dána vztahem

{\ displaystyle U = {N ^ {\ prime} \ varepsilon \ nad 2} + q \ varepsilon,}

protože v systému je kromě energie základního stavu každého oscilátoru celkem q energie. Někteří autoři, například Schroeder, tuto základní energii ve své definici celkové energie Einsteinovy pevné látky vynechávají.

Nyní jsme připraveni vypočítat teplotu

{\ displaystyle {1 \ přes T} = {\ částečné S \ přes \ částečné U} = {\ částečné S \ přes \ částečné q} {dq \ přes dU} = {1 \ přes \ varepsilon} {\ částečné S \ přes \ částečné q} = {k \ přes \ varepsilon} \ ln \ vlevo (1 + N ^ {\ prime} / q \ vpravo)}

Vyloučení q mezi dvěma předchozími vzorci dává pro U:

{\ displaystyle U = {N ^ {\ prime} \ varepsilon \ nad 2} + {N ^ {\ prime} \ varepsilon \ nad e ^ {\ varepsilon / kT} -1}.}

První člen je spojen s energií nulového bodu a nepřispívá k měrnému teplu. V dalším kroku tedy bude ztracen.

Diferenciací s ohledem na teplotu, kterou najdeme , získáme: ${\ displaystyle C_ {V}}$

{\ displaystyle C_ {V} = {\ částečné U \ nad \ částečné T} = {N ^ {\ prime} \ varepsilon ^ {2} \ nad kT ^ {2}} {e ^ {\ varepsilon / kT} \ nad \ doleva (e ^ {\ varepsilon / kT} -1 \ doprava) ^ {2}}}

nebo

${\ displaystyle C_ {V} = 3Nk \ left ({\ varepsilon \ over kT} \ right) ^ {2} {e ^ {\ varepsilon / kT} \ over \ left (e ^ {\ varepsilon / kT} -1 \ right) ^ {2}}.}$

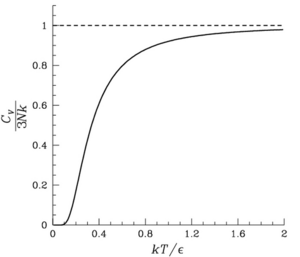
Ačkoli Einsteinův model tělesa přesně předpovídá tepelnou kapacitu při vysokých teplotách a v tomto limitu

${\ displaystyle \ lim _ {T \ rightarrow \ infty} C_ {V} = 3Nk}$ ,

což odpovídá zákonu Dulong – Petit .

Tepelná kapacita se nicméně při nízkých teplotách znatelně liší od experimentálních hodnot. Viz Debyeův model, jak vypočítat přesné nízkoteplotní tepelné kapacity.

Kanonický soubor

Tepelná kapacita se získává pomocí funkce kanonického dělení jednoduchého kvantového harmonického oscilátoru.

{\ displaystyle Z = \ sum _ {n = 0} ^ {\ infty} e ^ {- E_ {n} / kT}}

kde

{\ displaystyle E_ {n} = \ varepsilon \ left (n + {1 \ over 2} \ right)}

dosazením tohoto do vzorce funkce oddílu se získá výtěžek

{\ displaystyle {\ begin {aligned} Z = \ sum _ {n = 0} ^ {\ infty} e ^ {- \ varepsilon \ left (n + 1/2 \ right) / kT} = e ^ {- \ varepsilon / 2kT} \ sum _ {n = 0} ^ {\ infty} e ^ {- n \ varepsilon / kT} = e ^ {- \ varepsilon / 2kT} \ sum _ {n = 0} ^ {\ infty} \ left (e ^ {- \ varepsilon / kT} \ right) ^ {n} \\ = {e ^ {- \ varepsilon / 2kT} \ přes 1-e ^ {- \ varepsilon / kT}} = {1 \ přes e ^ {\ varepsilon / 2kT} -e ^ {- \ varepsilon / 2kT}} = {1 \ nad 2 \ sinh \ left ({\ varepsilon \ přes 2kT} \ right)}. \ end {zarovnáno}}}

Toto je funkce rozdělení jednoho harmonického oscilátoru. Protože statisticky jsou tepelná kapacita, energie a entropie pevné látky rovnoměrně rozloženy mezi její atomy, můžeme s touto funkcí rozdělení pracovat na získání těchto veličin a pak je jednoduše vynásobit, abychom získali součet. Dále vypočítáme průměrnou energii každého oscilátoru ${\ displaystyle N ^ {\ prime}}$

{\ displaystyle \ langle E \ rangle = U = - {1 \ nad Z} \ částečné _ {\ beta} Z}

kde

{\ displaystyle \ beta = {1 \ nad kT}.}

Proto,

{\ displaystyle U = -2 \ sinh \ left ({\ varepsilon \ nad 2kT} \ right) {- \ cosh \ left ({\ varepsilon \ nad 2kT} \ right) \ přes 2 \ sinh ^ {2} \ vlevo ({\ varepsilon \ nad 2kT} \ vpravo)} {\ varepsilon \ nad 2} = {\ varepsilon \ nad 2} \ coth \ left ({\ varepsilon \ nad 2kT} \ right).}

Tepelná kapacita jednoho oscilátoru je tedy

{\ displaystyle c_ {V} = {\ částečné U \ nad \ částečné T} = - {\ varepsilon \ nad 2} {1 \ nad \ sinh ^ {2} \ vlevo ({\ varepsilon \ nad 2kT} \ vpravo) } \ left (- {\ varepsilon \ nad 2kT ^ {2}} \ right) = k \ left ({\ varepsilon \ nad 2kT} \ right) ^ {2} {1 \ over \ sinh ^ {2} \ left ({\ varepsilon \ přes 2kT} \ vpravo)}.}

Doposud jsme počítali tepelnou kapacitu jedinečného stupně volnosti, který byl modelován jako kvantová harmonická. Tepelná kapacita celé pevné látky je pak dána vztahem , kde celkový počet stupňů volnosti pevné látky je třikrát (pro třísměrný stupeň volnosti) krát počet atomů v pevné látce. Jeden tak získá ${\ displaystyle C_ {V} = 3Nc_ {V}}$ ${\ displaystyle N}$

${\ displaystyle C_ {V} = 3Nk \ left ({\ varepsilon \ over 2kT} \ right) ^ {2} {1 \ over \ sinh ^ {2} \ left ({\ varepsilon \ over 2kT} \ right)} .}$

který je algebraicky identický se vzorcem odvozeným v předchozí části.

Veličina má rozměry teploty a je charakteristickou vlastností krystalu. Je známá jako Einsteinova teplota . Einsteinův model krystalů proto předpovídá, že energetické a tepelné kapacity krystalu jsou univerzální funkcí bezrozměrného poměru . Podobně model Debye předpovídá univerzální funkci poměru , kde je teplota Debye. ${\ displaystyle T _ {\ rm {E}} = \ varepsilon / k}$ ${\ displaystyle T / T _ {\ rm {E}}}$ ${\ displaystyle T / T _ {\ rm {D}}}$ ${\ displaystyle T _ {\ rm {D}}}$

Omezení a následný model

V Einsteinově modelu se specifické teplo blíží k nule exponenciálně rychle při nízkých teplotách. Je to proto, že všechny oscilace mají jednu společnou frekvenci. Správné chování lze zjistit kvantováním normálních režimů tělesa stejným způsobem, jaký navrhoval Einstein. Frekvence vln pak nejsou všechny stejné a specifické teplo jde na nulu jako zákon síly, který odpovídá experimentu. Tato úprava se nazývá model Debye , který se objevil v roce 1912. ${\ displaystyle T ^ {3}}$

Když se Walther Nernst dozvěděl o Einsteinově dokumentu z roku 1906 o specifickém ohni, byl tak nadšený, že cestoval s ním až z Berlína do Curychu.

Viz také

Kinetická teorie pevných látek

Reference

externí odkazy

Zeleny, Enrique. „Demonstrační projekt Wolfram - Einstein Solid“ . Citováno 2016-03-18 . .

Languages

In other projects