Speciální funkce definovaná integrálem
V matematice je exponenciální integrál Ei speciální funkcí na komplexní rovině . Je definován jako jeden konkrétní určitý integrál poměru mezi exponenciální funkcí a jejím argumentem .
Definice
Pro skutečné nenulové hodnoty x je exponenciální integrál Ei ( x ) definován jako

Risch algoritmus ukazuje, že Ei není elementární funkce . Výše uvedenou definici lze použít pro kladné hodnoty x , ale integrál je třeba chápat z hlediska Cauchyovy hlavní hodnoty kvůli singularitě integrandu na nule.
U komplexních hodnot argumentu se definice stává nejednoznačnou kvůli bodům větví na 0 a . Místo Ei se používá následující zápis,


Pro kladné hodnoty x máme .
Obecně platí, že řez větve se bere na záporné reálné ose a E 1 lze definovat analytickým pokračováním jinde v komplexní rovině.
Pro kladné hodnoty skutečné části lze toto zapsat


Chování E 1 v blízkosti řezu větve je možné vidět z následujícího vztahu:

Vlastnosti
Několik vlastností exponenciálního integrálu níže v určitých případech umožňuje vyhnout se jeho explicitnímu vyhodnocení pomocí výše uvedené definice.
Konvergentní série
Pro skutečné nebo složité argumenty mimo zápornou skutečnou osu lze vyjádřit jako


kde je konstanta Euler – Mascheroni . Součet konverguje pro celý komplex a my vezmeme obvyklou hodnotu komplexního logaritmu, který má řez větve podél záporné reálné osy.


Tento vzorec lze použít k výpočtu operací s pohyblivou řádovou čárkou pro reálné hodnoty od 0 do 2,5. Pro výsledek je nepřesné kvůli zrušení .



Ramanujan našel rychlejší konvergující sérii :

Tyto střídavé řady lze také použít k poskytnutí dobrých asymptotických hranic pro malá x, např .:

pro .

Asymptotická (divergentní) série
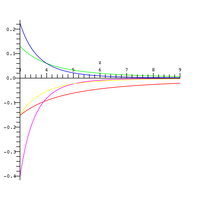
Relativní chyba asymptotické aproximace pro různý počet výrazů ve zkrácené sumě

Pro argumenty s větším modulem je bohužel konvergence výše uvedené řady pomalá. Například pro x = 10 je pro správnou odpověď na tři platné číslice pro vyžadováno více než 40 výrazů . Existuje však divergentní aproximace řady, kterou lze získat integrací po částech:



který má chybu objednávky a je platný pro velké hodnoty . Relativní chyba výše uvedené aproximace je vynesena na obrázku vpravo pro různé hodnoty , počet členů ve zkráceném součtu ( červeně, růžově).





Exponenciální a logaritmické chování: bracketing

Bracketing elementárních funkcí

Ze dvou řad navržených v předchozích podsekcích vyplývá, že se chová jako negativní exponenciál pro velké hodnoty argumentu a jako logaritmus pro malé hodnoty. Pro kladné reálné hodnoty argumentu mohou být složené závorky elementárních funkcí následovně:



Levá strana této nerovnosti je v grafu znázorněna vlevo modře; střední část je zobrazena černě a pravá strana je zobrazena červeně.

Definice Ein
Oba a mohou být zapsány jednodušeji pomocí celé funkce definované jako




(Všimněte si, že toto je jen střídající se řada ve výše uvedené definici ). Pak máme



Vztah s jinými funkcemi
Kummerova rovnice

je obvykle řešeno splývajícími hypergeometrickými funkcemi a Ale když a to je,





my máme

pro všechny z . Druhé řešení je pak dáno E 1 ( - z ). Ve skutečnosti,
![{\ Displaystyle E_ {1} (-z) =-\ gamma -i \ pi +{\ frac {\ částečný [U (a, 1, z) -M (a, 1, z)]} {\ částečný a }}, \ qquad 0 <{\ rm {Arg}} (z) <2 \ pi}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baf776ea1a2dea96558b4a7f2cf7bae3d8cad7ac)
s derivátem vyhodnoceným na Další souvislosti s konfluentními hypergeometrickými funkcemi je, že E 1 je exponenciální doba funkce U (1,1, z ):


Exponenciální integrál podle vzorce úzce souvisí s logaritmickou integrální funkcí li ( x )

pro nenulové skutečné hodnoty .

Zobecnění
Exponenciální integrál lze také zobecnit na

což lze zapsat jako zvláštní případ neúplné funkce gama :

Zobecněnému tvaru se někdy říká funkce Misra , definovaná jako


Mnoho vlastností této generalizované formy lze nalézt v digitální knihovně matematických funkcí NIST.
Včetně logaritmu definuje generalizovanou integro-exponenciální funkci

Neurčitý integrál:

je podobný ve formě k obvyklému funkci generující pro , počet dělitele z :



Deriváty
Deriváty generalizovaných funkcí lze vypočítat pomocí vzorce


Všimněte si, že tuto funkci lze snadno vyhodnotit (díky čemuž je tato rekurze užitečná), protože je spravedlivá .


Exponenciální integrál imaginárního argumentu
Pokud je imaginární, má nezápornou skutečnou část, takže můžeme použít vzorec


získat vztah s goniometrickými integrály a :


![{\ Displaystyle E_ {1} (ix) = i \ left [-{\ tfrac {1} {2}} \ pi +\ operatorname {Si} (x) \ right]-\ operatorname {Ci} (x) \ qquad (x> 0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc6245104e0362c31571f3abda13b3f5f06d06c9)
Skutečné a imaginární části jsou vykresleny na obrázku vpravo s černými a červenými křivkami.

Aproximace
Pro exponenciální integrální funkci došlo k řadě přiblížení. Tyto zahrnují:
- Sbližování Swamee a Ohija

kde
![{\ displaystyle {\ begin {aligned} A & = \ ln \ left [\ left ({\ frac {0,56146} {x}}+0,65 \ right) (1+x) \ right] \\ B & = x^{4 } e^{7,7x} (2+x)^{3,7} \ end {zarovnaný}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2fee0fd224536a437d20c1e057ed6ed4187b21d)
- Allenova a Hastingsova aproximace

kde
![{\ Displaystyle {\ begin {aligned} {\ textbf {a}} & \ triangleq [-0,57722,0,99999, -0,24991,0,05519, -0,00976,0,00108]^{T} \\ {\ textbf {b}} & \ triangleq [0.26777,8.63476,18.05902,8.57333]^{T} \\ {\ textbf {c}} & \ triangleq [3.95850,21.09965,25.63296,9.57332]^{T} \\ {\ textbf {x}} _ { k} & \ triangleq [x^{0}, x^{1}, \ tečky, x^{k}]^{T} \ end {zarovnáno}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd59588e32d86da6a1545610b3b27d9f8ec38b7f)
- Pokračující expanze frakcí

- Sbližování Barry et al.
![{\ Displaystyle E_ {1} (x) = {\ frac {e^{-x}} {G+(1-G) e^{-{\ frac {x} {1-G}}}}} \ ln \ left [1+{\ frac {G} {x}}-{\ frac {1-G} {(h+bx)^{2}}} \ right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90bab5b2a5c683e40d3dbf066bf2b79160d692b)
kde:

s bytí Eulerova konstanta .
Aplikace
- Časově závislý přenos tepla
- Nevyrovnané proudění podzemní vody v Theisově řešení (nazývá se funkce studny )
- Radiační přenos ve hvězdné a planetární atmosféře
- Rovnice radiální difuzivity pro přechodný nebo nestabilní tok s linkovými zdroji a propady
- Řešení neutronové transportní rovnice ve zjednodušených 1-D geometriích
Viz také
Poznámky
Reference
-
Abramowitz, Milton; Irene Stegun (1964). Příručka matematických funkcí se vzorci, grafy a matematickými tabulkami . Abramowitz a Stegun . New York: Dover. ISBN 978-0-486-61272-0., Kapitola 5 .
-
Bender, Carl M .; Steven A. Orszag (1978). Pokročilé matematické metody pro vědce a inženýry . McGraw -Hill. ISBN 978-0-07-004452-4.
-
Bleistein, Norman; Richard A. Handelsman (1986). Asymptotická rozšíření integrálů . Dover. ISBN 978-0-486-65082-1.
-
Busbridge, Ida W. (1950). „O integro-exponenciální funkci a hodnocení některých integrálů, které ji zahrnují“. Kvart. J. Math. (Oxford) . 1 (1): 176–184. Bibcode : 1950QJMat ... 1..176B . doi : 10,1093/qmath/1.1.176 .
-
Stankiewicz, A. (1968). „Tabulky integro-exponenciálních funkcí“. Acta Astronomica . 18 : 289. Bibcode : 1968AcA .... 18..289S .
-
Sharma, RR; Zohuri, Bahman (1977). „Obecná metoda pro přesné vyhodnocení exponenciálních integrálů E 1 (x), x> 0“. J. Comput. Fyz . 25 (2): 199–204. Bibcode : 1977JCoPh..25..199S . doi : 10,1016/0021-9991 (77) 90022-5 .
-
Kölbig, KS (1983). „Na integrálním exp ( - μt ) t ν − 1 log m t dt “ . Matematika. Výpočet . 41 (163): 171–182. doi : 10,1090/S0025-5718-1983-0701632-1 .
-
Milgram, MS (1985). „Zobecněná integro-exponenciální funkce“ . Matematika výpočtu . 44 (170): 443–458. doi : 10,1090/S0025-5718-1985-0777276-4 . JSTOR 2007964 . MR 0777276 .
-
Misra, Rama Dhar; Narozen, M. (1940). „O stabilitě krystalových mřížek. II“. Matematický sborník Cambridgeské filozofické společnosti . 36 (2): 173. Bibcode : 1940PCPS ... 36..173M . doi : 10,1017/S030500410001714X .
-
Chiccoli, C .; Lorenzutta, S .; Maino, G. (1988). „O hodnocení generalizovaných exponenciálních integrálů E ν (x)“. J. Comput. Fyz . 78 (2): 278–287. Bibcode : 1988JCoPh..78..278C . doi : 10,1016/0021-9991 (88) 90050-2 .
-
Chiccoli, C .; Lorenzutta, S .; Maino, G. (1990). „Nedávné výsledky pro generalizované exponenciální integrály“ . Počítačová matematika. Žádost . 19 (5): 21–29. doi : 10,1016/0898-1221 (90) 90098-5 .
-
MacLeod, Allan J. (2002). „Efektivní výpočet některých generalizovaných exponenciálních integrálů“ . J. Comput. Appl. Math . 148 (2): 363–374. Bibcode : 2002JCoAm.138..363M . doi : 10.1016/S0377-0427 (02) 00556-3 .
-
Stiskněte, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), „Část 6.3. Exponenciální integrály“ , Numerical Recipes: The Art of Scientific Computing (3. vyd.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
-
Temme, NM (2010), „Exponenciální, logaritmické, sinusové a kosinové integrály“ , v Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
externí odkazy











































![{\ Displaystyle E_ {1} (-z) =-\ gamma -i \ pi +{\ frac {\ částečný [U (a, 1, z) -M (a, 1, z)]} {\ částečný a }}, \ qquad 0 <{\ rm {Arg}} (z) <2 \ pi}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baf776ea1a2dea96558b4a7f2cf7bae3d8cad7ac)





















![{\ Displaystyle E_ {1} (ix) = i \ left [-{\ tfrac {1} {2}} \ pi +\ operatorname {Si} (x) \ right]-\ operatorname {Ci} (x) \ qquad (x> 0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc6245104e0362c31571f3abda13b3f5f06d06c9)


![{\ displaystyle {\ begin {aligned} A & = \ ln \ left [\ left ({\ frac {0,56146} {x}}+0,65 \ right) (1+x) \ right] \\ B & = x^{4 } e^{7,7x} (2+x)^{3,7} \ end {zarovnaný}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2fee0fd224536a437d20c1e057ed6ed4187b21d)

![{\ Displaystyle {\ begin {aligned} {\ textbf {a}} & \ triangleq [-0,57722,0,99999, -0,24991,0,05519, -0,00976,0,00108]^{T} \\ {\ textbf {b}} & \ triangleq [0.26777,8.63476,18.05902,8.57333]^{T} \\ {\ textbf {c}} & \ triangleq [3.95850,21.09965,25.63296,9.57332]^{T} \\ {\ textbf {x}} _ { k} & \ triangleq [x^{0}, x^{1}, \ tečky, x^{k}]^{T} \ end {zarovnáno}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd59588e32d86da6a1545610b3b27d9f8ec38b7f)

![{\ Displaystyle E_ {1} (x) = {\ frac {e^{-x}} {G+(1-G) e^{-{\ frac {x} {1-G}}}}} \ ln \ left [1+{\ frac {G} {x}}-{\ frac {1-G} {(h+bx)^{2}}} \ right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90bab5b2a5c683e40d3dbf066bf2b79160d692b)
