Faktorizace - Factorization
V matematice , faktorizace (nebo faktorizace naleznete English rozdíly hláskování ), nebo factoring se skládá z psaní číslo nebo jiný matematický objekt jako součin několika faktorů , obvykle menší nebo jednodušších objektů stejného druhu. Například 3 × 5 je faktorizace celého čísla 15 a ( x - 2) ( x + 2) je faktorizace polynomu x 2 - 4 .
Faktorizace není obvykle považována za smysluplnou v číselných systémech s dělením , jako jsou reálná nebo komplexní čísla , protože jakékoli lze triviálně zapsat, jako vždy, když není nula. Smysluplnou faktorizaci pro racionální číslo nebo racionální funkci však lze získat tak, že ji napíšeme v nejnižších termínech a oddělíme faktoring jejího čitatele a jmenovatele.
Faktorizace byla poprvé zvažována starověkými řeckými matematiky v případě celých čísel. Dokázali základní teorém aritmetiky , který tvrdí, že každé kladné celé číslo může být započítáno do součinu prvočísel , které nelze dále započítat do celých čísel větších než 1. Navíc je tato faktorizace jedinečná až do pořadí faktorů. Ačkoli je celočíselná faktorizace druhem inverze k násobení, je to algoritmicky mnohem obtížnější , což je skutečnost, která se v kryptosystému RSA využívá k implementaci kryptografie s veřejným klíčem .
Polynomiální faktorizace byla také studována po staletí. V elementární algebře faktoring polynomu redukuje problém nalezení jeho kořenů na nalezení kořenů faktorů. Polynomy s koeficienty v celých číslech nebo v poli mají jedinečnou faktorizační vlastnost , což je verze základní věty o aritmetice s prvočísly nahrazenými neredukovatelnými polynomy . Zejména univariační polynom se složitými koeficienty připouští jedinečnou (až do uspořádání) faktorizaci na lineární polynomy : toto je verze základní věty algebry . V tomto případě lze faktorizaci provést pomocí algoritmů pro hledání kořenů . Případ polynomů s celočíselnými koeficienty je zásadní pro počítačovou algebru . Existují efektivní počítačové algoritmy pro výpočet (úplné) faktorizace v kruhu polynomů s koeficienty racionálních čísel (viz faktorizace polynomů ).
Komutativní kroužek mající jedinečnou rozklad vlastnost se nazývá jedinečné faktorizace doména . Existují číselné systémy , například určité prstence algebraických celých čísel , které nejsou jedinečnými doménami faktorizace. Kruhy algebraických celých čísel však uspokojují slabší vlastnosti Dedekindových domén : ideály faktor jedinečně do prvotních ideálů .
Faktorizace může také odkazovat na obecnější dekompozice matematického objektu na součin menších nebo jednodušších objektů. Například každá funkce může být zahrnuta do složení surjektivní funkce s injektivní funkcí . Matice mají mnoho druhů maticových faktorizací . Například každá matice má jedinečnou faktorizaci LUP jako součin nižší trojúhelníkové matice L se všemi diagonálními vstupy rovnými jedné, horní trojúhelníkové matice U a permutační matice P ; toto je maticová formulace Gaussovy eliminace .
Celá čísla
Podle základní věty o aritmetice má každé celé číslo větší než 1 jedinečnou (až na pořadí faktorů) faktorizaci na prvočísla , což jsou taková celá čísla, která nelze dále faktorizovat na součin celých čísel větších než jedna.
Pro výpočet rozklad celé číslo n , jeden potřebuje algoritmus pro nalezení dělitel q z n a rozhodování o tom, že n je prvočíslo. Když je takový dělitel nalezen, opakovaná aplikace tohoto algoritmu na faktory q a n / q nakonec poskytne úplnou faktorizaci n .
Pro nalezení dělitel q z n , pokud existuje, stačí otestovat všechny hodnoty q tak, že 1 <q a q 2 ≤ n . Ve skutečnosti, pokud r je dělitel n takový, že r 2 > n , pak q = n / r je dělitel n takový, že q 2 ≤ n .
Pokud testujeme hodnoty q ve vzestupném pořadí, první nalezený dělitel je nutně prvočíslo a kofaktor r = n / q nemůže mít žádný dělitel menší než q . K získání úplné faktorizace stačí tedy pokračovat v algoritmu hledáním dělitel r, který není menší než q a není větší než √ r .
Pro použití metody není třeba testovat všechny hodnoty q . V zásadě stačí testovat pouze primární dělitele. To musí mít tabulku prvočísel, která může být generována například pomocí síta Eratosthenes . Protože metoda faktorizace funguje v podstatě stejně jako síto Eratosthenes, je obecně efektivnější testovat na dělitel pouze ta čísla, u nichž není hned jasné, zda jsou prvočísla nebo ne. Obvykle lze postupovat testováním 2, 3, 5 a čísel> 5, jejichž poslední číslice je 1, 3, 7, 9 a součet číslic není násobkem 3.
Tato metoda funguje dobře pro faktoring malých celých čísel, ale je neúčinná pro větší celá čísla. Například Pierre de Fermat nebyl schopen zjistit, že 6. číslo Fermat
není prvočíslo. Ve skutečnosti by aplikace výše uvedené metody vyžadovala více než10 000 divizí pro číslo, které má 10 desetinných míst .
Existují účinnější algoritmy faktoringu. Zůstávají však relativně neefektivní, protože při současném stavu techniky nelze ani u výkonnějších počítačů rozložit faktor na 500 desetinných číslic, který je součinem dvou náhodně vybraných prvočísel. Tím je zajištěna bezpečnost kryptosystému RSA , který je široce používán pro zabezpečenou internetovou komunikaci.
Příklad
Pro faktoring n = 1386 do prvočísel:
- Začněte dělením 2: číslo je sudé a n = 2 · 693 . Pokračujte číslem 693 a 2 jako první dělitel.
- 693 je lichý (2 není dělitel), ale je násobkem 3: jeden má 693 = 3 · 231 a n = 2 · 3 · 231 . Pokračujte 231 a 3 jako první dělitel kandidát.
- 231 je také násobkem 3: jeden má 231 = 3,7 , a tedy n = 2 · 3 2 · 77 . Pokračujte číslem 77 a 3 jako první dělitel.
- 77 není násobkem 3, protože součet jeho číslic je 14, není násobkem 3. Rovněž to není násobek 5, protože jeho poslední číslice je 7. Další lichý dělitel, který se má testovat, je 7. Jeden má 77 = 7 · 11 , a tedy n = 2 · 3 2 · 7 · 11 . To ukazuje, že 7 je primární (snadno se testuje přímo). Pokračujte čísly 11 a 7 jako kandidát prvního dělitele.
- Jako 7 2 > 11 jedna skončila. 11 je tedy prvočíslo a primární faktorizace je
- 1386 = 2 · 3 2 · 7 · 11 .
Výrazy
Manipulace s výrazy je základem algebry . Faktorizace je jednou z nejdůležitějších metod pro manipulaci s výrazem z několika důvodů. Pokud lze dát rovnici do faktorizované podoby E ⋅ F = 0 , pak se problém řešení rovnice rozdělí na dva nezávislé (a obecně jednodušší) problémy E = 0 a F = 0 . Když lze výraz zohlednit, faktory jsou často mnohem jednodušší a mohou tak nabídnout určitý náhled na problém. Například,
16 násobení, 4 odčítání a 3 sčítání může být zapracováno do mnohem jednoduššího výrazu
pouze se dvěma násobeními a třemi odečty. Faktorovaný tvar navíc okamžitě dává kořeny x = a , b , c jako kořeny polynomu.
Na druhou stranu faktorizace není vždy možná, a když je to možné, faktory nejsou vždy jednodušší. Například lze rozdělit na dva neredukovatelné faktory a .
Pro nalezení faktorizace byly vyvinuty různé metody; některé jsou popsány níže .
Na řešení algebraických rovnic lze pohlížet jako na problém polynomiální faktorizace. Ve skutečnosti lze základní větu algebry vyjádřit následovně: každý polynom v x stupně n s komplexními koeficienty může být faktorizován do n lineárních faktorů pro i = 1, ..., n , kde a i s jsou kořeny polynomu. I přesto, že struktura faktorizace je v těchto případech je znám, i to obecně nemohou být vypočteny z hlediska zbytků ( n th kořeny), u Abel-Ruffini teorém . Ve většině případů lze nejlépe provést výpočet přibližných hodnot kořenů pomocí algoritmu pro hledání kořenů .
Historie faktorizace výrazů
Systematické používání algebraických manipulací pro zjednodušování výrazů (konkrétněji rovnic )) lze datovat do 9. století s al-Khwarizmiho knihou The Compendious Book on Calculation by Completion and Balancing , která je pojmenována dvěma takovými druhy manipulace.
Avšak ani pro řešení kvadratických rovnic nebyla faktoringová metoda použita před Harriotovou prací publikovanou v roce 1631, deset let po jeho smrti. Ve své knize Artis Analyticae Praxis reklama Aequationes Algebraicas Resolvendas , Harriot nakreslil, stoly pro sčítání, odčítání, násobení a dělení monomials , dvojčleny a trinomials . Potom ve druhé části nastavil rovnici aa - ba + ca = + bc a ukázal, že to odpovídá formě násobení, kterou předtím poskytl, což dává faktorizaci ( a - b ) ( a + c ) .
Obecné metody
Následující metody platí pro jakýkoli výraz, který je součtem nebo který lze převést na součet. Proto jsou nejčastěji aplikovány na polynomy , i když je lze použít také v případě, že podmínky součtu nejsou monomiální , to znamená, že podmínky součtu jsou součinem proměnných a konstant.
Společný faktor
Může se stát, že všechny podmínky částky jsou produkty a že některé faktory jsou společné pro všechny podmínky. V tomto případě distribuční právo umožňuje rozdělit tento společný faktor. Pokud existuje několik takových společných faktorů, stojí za to rozdělit ten největší společný faktor. Pokud existují celočíselné koeficienty, lze také vyloučit největšího společného dělitele těchto koeficientů.
Například,
protože 2 je největší společný dělitel 6, 8 a 10 a dělí všechny výrazy.
Seskupení
Seskupovací podmínky mohou umožňovat použití jiných metod pro získání faktorizace.
Například faktorovat
lze poznamenat, že první dva termíny mají společný faktor x a poslední dva termíny mají společný faktor y . Tím pádem
Poté jednoduchá kontrola ukazuje společný faktor x + 5 , což vede k faktorizaci
Obecně to funguje pro částky 4 výrazů, které byly získány jako součin dvou binomů . I když to není často, může to fungovat i u složitějších příkladů.
Sčítání a odčítání výrazů
Někdy se může stát, že některé seskupení výrazů bude součástí rozpoznatelného vzoru . Potom je užitečné přidat termíny pro dokončení vzoru a odečíst je, pokud neměníte hodnotu výrazu.
Typickým použitím je dokončení metody square pro získání kvadratického vzorce .
Dalším příkladem je faktorizace: Pokud člověk zavádí nereálnou odmocninu –1 , běžně označovanou i , pak má rozdíl čtverců
Lze však také chtít faktorizaci s reálnými číselnými koeficienty. Sečtením a odečtením a seskupením tří výrazů dohromady lze rozpoznat čtverec binomické :
Odečtením a přidáním také získáte faktorizaci:
Tyto faktorizace fungují nejen na komplexních číslech, ale také na libovolném poli , kde –1, 2 nebo –2 je čtverec. V konečném poli je součin dvou jiných než čtverců čtverec; to znamená, že polynom, který je neredukovatelný na celá čísla, je redukovatelné modulo každé prvočíslo . Například,
- od té doby
- od té doby
- od té doby
Rozpoznatelné vzory
Mnoho identit poskytuje rovnost mezi součtem a produktem. Výše uvedené metody lze použít k tomu, aby se souhrnná stránka určité identity objevila ve výrazu, který může být proto nahrazen produktem.
Níže jsou uvedeny identity, jejichž levé strany se běžně používají jako vzory (to znamená, že proměnné E a F, které se v těchto identitách objevují, mohou představovat jakýkoli podvýraz výrazu, který je třeba faktorizovat.
- Například,
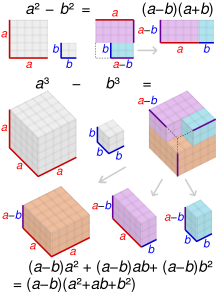
- Součet/rozdíl dvou kostek
- Rozdíl dvou čtvrtých mocností
- Součet/rozdíl dvou n -tých mocnin
- U následujících identit mohou být faktory často dále faktorizovány:
- Rozdíl, dokonce exponent
- Rozdíl, sudý nebo lichý exponent
- Toto je příklad, který ukazuje, že faktory mohou být mnohem větší než součet, který je faktorizován.
- Součet, lichý exponent
- (získané změnou F o - F v předchozím vzorci)
- Součet, dokonce exponent
- Pokud je exponent mocninou dvou, pak výraz nelze obecně faktorizovat bez zavedení komplexních čísel (pokud E a F obsahují komplexní čísla, nemusí tomu tak být). Pokud má n lichý dělitel, to znamená, že pokud n = pq s p lichým, lze použít předchozí vzorec (v „součtu, lichý exponent“) aplikovaný na
- Trojčleny a krychlové vzorce
- Binomická rozšíření
- Tyto binomické poučky dodává vzory, které mohou být snadno rozpozná z celých čísel, které se objevují v nich
- V nízké míře:
- Obecněji řečeno, koeficienty rozšířených forem a jsou binomické koeficienty , které se objevují v n -té řadě Pascalova trojúhelníku .
Kořeny jednoty
N th kořeny jednoty jsou komplexní čísla , z nichž každý se o kořen polynomu Jsou tedy čísla
pro
Z toho vyplývá, že pro jakékoli dva výrazy E a F má jeden:
Pokud E a F jsou skutečné výrazy a člověk chce skutečné faktory, musí nahradit každý pár komplexních konjugovaných faktorů jeho součinem. Protože komplexní konjugát je a
jeden má následující skutečné faktorizace (jeden přechází z jednoho do druhého změnou k na n - k nebo n + 1 - k a použitím obvyklých trigonometrických vzorců :
Tyto kosiny , které se objevují v těchto factorizations jsou algebraická čísla , a může být vyjádřena z hlediska zbytků (to je možné proto, že jejich Galois skupina je cyklická); tyto radikální výrazy jsou však příliš složité na to, aby byly použity, s výjimkou nízkých hodnot n . Například,
Často chce někdo faktorizaci s racionálními koeficienty. Taková faktorizace zahrnuje cyklotomické polynomy . Vyjadřovat racionální factorizations částek a rozdíly nebo pravomoci, potřebujeme zápis pro homogenizaci polynom : pokud její homogenizace je bivariate polynom Tak, jeden má
kde produkty jsou převzaty všechny dělitelé n nebo všechny dělitelé 2 n , které nerozdělují n , a je n -tým cyklotomickým polynomem.
Například,
protože dělitelé 6 jsou 1, 2, 3, 6 a dělitelé 12, kteří nerozdělují 6, jsou 4 a 12.
Polynomy
U polynomů je faktorizace silně spojena s problémem řešení algebraických rovnic . Algebraická rovnice má tvar
kde P ( x ) je polynom v x s Roztok této rovnice (která se také nazývá kořen polynomu) je hodnota r o x tak, že
Pokud je faktorizace P ( x ) = 0 jako součin dvou polynomů, pak kořeny P ( x ) jsou spojením kořenů Q ( x ) a kořenů R ( x ) . Řešení P ( x ) = 0 se tedy redukuje na jednodušší úlohy řešení Q ( x ) = 0 a R ( x ) = 0 .
Naopak, faktor věta uvádí, že, je-li r je kořen P ( x ) = 0 , pak P ( x ) mohou být zapracovány jako
kde Q ( x ) je kvocient euklidovské dělení z P ( x ) = 0 o lineární (studia jednoho) faktor x - r .
V případě, že koeficienty P ( x ) je reálná nebo komplexní čísla, má základní věta algebry tvrdí, že P ( x ) je skutečný nebo komplexní kořen. Rekurzivně s využitím faktorové věty to má za následek, že
kde jsou skutečné nebo komplexní kořeny P , přičemž některé z nich se možná opakují. Tato úplná faktorizace je jedinečná až do pořadí faktorů.
Pokud jsou koeficienty P ( x ) reálné, obecně se chce faktorizace, kde faktory mají skutečné koeficienty. V tomto případě může mít úplná faktorizace některé kvadratické (stupeň dva) faktory. Tuto faktorizaci lze snadno odvodit z výše uvedené úplné faktorizace. Ve skutečnosti, pokud r = a + ib je nereálný kořen P ( x ) , pak jeho komplexní konjugát s = a - ib je také kořenem P ( x ) . Takže produkt
je faktor P ( x ) se skutečnými koeficienty. Opakováním pro všechny nereálné faktory získáte faktorizaci s lineárními nebo kvadratickými reálnými faktory.
Pro výpočet těchto skutečných nebo složitých faktorizací je třeba kořeny polynomu, které nemusí být vypočítány přesně a pouze aproximovány pomocí algoritmů pro vyhledávání kořenů .
V praxi má většina zájmových algebraických rovnic celočíselné nebo racionální koeficienty a člověk může chtít faktorizaci s faktory stejného druhu. Základní věta aritmetiky lze zobecnit na tento případ s tím, že polynomy s integer nebo racionálními koeficienty mají jedinečnou vlastnost faktorizace . Přesněji, každý polynom s racionálními koeficienty může být v produktu faktorizován
kde q je racionální číslo a jsou nekonstantní polynomy s celočíselnými koeficienty, které jsou neredukovatelné a primitivní ; to znamená, že žádný z nich nesmí být zapsán jako součin dvou polynomů (s celočíselnými koeficienty), které nejsou ani 1 ani –1 (celá čísla jsou považována za polynomy stupně nula). Tato faktorizace je navíc jedinečná až do pořadí faktorů a znaků faktorů.
Pro výpočet této faktorizace existují účinné algoritmy , které jsou implementovány ve většině systémů počítačové algebry . Viz faktorizace polynomů . Tyto algoritmy jsou bohužel příliš komplikované na použití pro výpočty typu papír a tužka. Kromě výše uvedené heuristiky je pro ruční výpočty vhodné pouze několik metod, které obecně fungují pouze pro polynomy nízkého stupně s několika nenulovými koeficienty. Hlavní takové metody jsou popsány v následujících podsekcích.
Faktorizace primitivní části a obsahu
Každý polynom s racionálními koeficienty může být faktorizován jedinečným způsobem jako součin racionálního čísla a polynomu s celočíselnými koeficienty, který je primitivní (to znamená, že největší společný dělitel koeficientů je 1) a má kladný vedoucí koeficient (koeficient termínu nejvyššího stupně). Například:
Při této faktorizaci se racionální číslo nazývá obsah a primitivní polynom je primitivní část . Výpočet této faktorizace lze provést následujícím způsobem: za prvé redukujte všechny koeficienty na společného jmenovatele, abyste získali kvocient o celé číslo q polynomu s celočíselnými koeficienty. Potom se rozdělí větší společný dělitel p koeficientů tohoto polynomu pro získání primitivní části, přičemž obsah je Nakonec, pokud je to potřeba, změní se znaménka p a všechny koeficienty primitivní části.
Tato faktorizace může vést k výsledku, který je větší než původní polynom (typicky když existuje mnoho společných jmenovatelů), ale i když je tomu tak, s primitivní částí se obecně snáze manipuluje pro další faktorizaci.
Pomocí faktorové věty
Faktor teorém říká, že pokud r se o kořen z polynomu
což znamená P ( r ) = 0 , pak existuje faktorizace
kde
s . Pak polynomiální dlouhé dělení nebo syntetické dělení dává:
To může být užitečné, když člověk ví nebo může uhodnout kořen polynomu.
Například pro člověka může být snadno vidět, že součet jeho koeficientů je 0, takže r = 1 je kořen. As r + 0 = 1 , a jeden má
Racionální kořeny
U polynomů s koeficienty racionálních čísel lze hledat kořeny, které jsou racionálními čísly. Primitivní faktorizace částečného obsahu (viz výše ) redukuje problém hledání racionálních kořenů na případ polynomů s celočíselnými koeficienty, které nemají netriviálního společného dělitele .
If je racionální kořen takového polynomu
faktorová věta ukazuje, že člověk má faktorizaci
kde oba faktory mají celočíselné koeficienty (skutečnost, že Q má celočíselné koeficienty, vyplývá z výše uvedeného vzorce pro podíl P ( x ) podle ).
Porovnání koeficientů stupně n a konstantních koeficientů ve výše uvedené rovnosti ukazuje, že je -li racionální kořen v redukované formě , pak q je dělitelem a p je dělitelem Proto existuje konečný počet možností pro p a q , které lze systematicky zkoumat.
Například pokud je polynom
má racionální kořen s q > 0 , pak p musí dělit 6; to je a q musí dělit 2, to znamená, že navíc, pokud x <0 , všechny členy polynomu jsou záporné, a proto kořen nemůže být záporný. To znamená, že člověk musí mít
Přímý výpočet ukazuje, že pouze root je, takže nemůže existovat žádný jiný racionální root. Použití faktorové věty nakonec vede k faktorizaci
Kvadratická metoda AC
Výše uvedený způsob lze upravit pro kvadratické polynomy , což vede k ac faktorizační metodě .
Zvažte kvadratický polynom
s celočíselnými koeficienty. Pokud se má racionální kořen, musí být jeho jmenovatel rozdělit rovnoměrně, a to může být psáno jako možná redukovatelné frakci By viètovy vzorce , druhý kořen je
s Tedy druhý kořen je také racionální a Vietův druhý vzorec dává
to je
Kontrola všech párů celých čísel, jejichž součinem je ac, poskytne racionální kořeny, pokud existují.
Uvažujme například kvadratický polynom
Kontrola faktorů ac = 36 vede k 4 + 9 = 13 = b , čímž získáme dva kořeny
a faktorizace
Použití vzorců pro polynomické kořeny
Libovolný univariantní kvadratický polynom lze založit pomocí kvadratického vzorce :
kde a jsou dva kořeny polynomu.
Pokud jsou a, b, c všechny reálné , pak jsou faktory reálné právě tehdy, pokud diskriminant není záporný. V opačném případě nelze kvadratický polynom faktorizovat na nekonstantní reálné faktory.
Kvadratická rovnice je platná, pokud koeficienty do žádné oblasti z charakteristického odlišný od dvou, a zejména na koeficienty v konečného pole s lichým počtem prvků.
Existují také vzorce pro kořeny krychlových a kvartických polynomů, které jsou obecně pro praktické použití příliš komplikované. Tyto Abel-Ruffini věta ukazuje, že neexistují žádné obecné kořenové vzorce, pokud jde o zbytky pro polynomy stupně pět nebo vyšší.
Využití vztahů mezi kořeny
Může se stát, že člověk zná nějaký vztah mezi kořeny polynomu a jeho koeficienty. Použití těchto znalostí může pomoci faktoring polynomu a nalezení jeho kořenů. Galoisova teorie je založena na systematickém studiu vztahů mezi kořeny a koeficienty, které zahrnují Vietovy vzorce .
Zde uvažujeme jednodušší případ, kdy vztah uspokojují dva kořeny a polynom
kde Q je polynom.
To znamená, že je společným kořenem a Jeho je tedy kořenem největšího společného dělitele těchto dvou polynomů. Z toho vyplývá, že tento největší společný dělitel je nekonstantním faktorem euklidovského algoritmu pro polynomy, který umožňuje vypočítat tento největší společný faktor.
Pokud například někdo ví nebo hádá, že: má dva kořeny, které se sčítají na nulu, lze použít euklidovský algoritmus na a První krok dělení spočívá v přidání k získání zbytku
Poté, dělení podle dává nulu jako nový zbytek a x - 5 jako podíl, což vede k úplné faktorizace
Unikátní faktorizační domény
Celá čísla a polynomy nad polem sdílejí vlastnost jedinečné faktorizace, to znamená, že každý nenulový prvek může být zapracován do součinu invertibilního prvku ( jednotka , ± 1 v případě celých čísel) a součinu neredukovatelných prvků ( prvočísla , v případě celých čísel), a tato faktorizace je jedinečná až do přeskupení faktorů a přesunu jednotek mezi faktory. Integrální domény, které sdílejí tuto vlastnost, se nazývají jedinečné faktorizační domény (UFD).
V UFD existují největší společní dělitelé a naopak každá integrální doména, ve které existují největší společní dělitelé, je UFD. Každá hlavní ideální doména je UFD.
Euclidean doména je nedílnou domény, na kterém je definována euklidovské dělení podobný tomu z celých čísel. Každá euklidovská doména je hlavní ideální doménou, a tedy UFD.
V euklidovské doméně umožňuje euklidovské dělení definování euklidovského algoritmu pro výpočet největších společných dělitelů. To však neznamená existenci faktorizačního algoritmu. Existuje explicitní příklad pole F , takže v euklidovské doméně F [ x ] univariačních polynomů nad F nemůže existovat žádný faktorizační algoritmus .
Ideály
V teorii algebraických čísel vedlo studium diofantických rovnic v průběhu 19. století matematiky k zavedení generalizací celých čísel zvaných algebraická celá čísla . První prsten algebraických celých čísel , které byly zvažovány, byla Gaussova celá a Eisensteinova celá čísla , která sdílejí s obvyklými celými čísly tu vlastnost, že jsou hlavními ideálními doménami , a mají tedy jedinečnou vlastnost faktorizace .
Bohužel se brzy ukázalo, že většina prstenců algebraických celých čísel není hlavní a nemá jedinečnou faktorizaci. Nejjednodušší příklad je ve kterém
a všechny tyto faktory jsou neredukovatelné .
Tento nedostatek jedinečné faktorizace je hlavní obtíž při řešení diofantických rovnic. Například mnoho špatných důkazů Fermatovy poslední věty (pravděpodobně včetně Fermatova „skutečně úžasného důkazu toho, který je tento okraj příliš úzký na to, aby obsahoval“ ) bylo založeno na implicitním předpokladu jedinečné faktorizace.
Tuto obtíž vyřešil Dedekind , který dokázal, že prstence algebraických celých čísel mají jedinečnou faktorizaci ideálů : v těchto prstencích je každý ideál produktem prvotních ideálů a tato faktorizace je jedinečná podle pořadí faktorů. Tyto obory integrity , které mají tuto jedinečnou vlastnost faktorizace se nyní nazývají dedekindův obor . Mají mnoho pěkných vlastností, které je činí základními v teorii algebraických čísel.
Matice
Maticové prstence jsou nekomutativní a nemají jedinečnou faktorizaci: obecně existuje mnoho způsobů, jak psát matici jako produkt matic. Problém faktorizace tedy spočívá v hledání faktorů specifikovaných typů. Například, LU rozklad poskytuje matici jako produkt, jehož dolní trojúhelníkovou matici pomocí horní trojúhelníkovou matici . Protože to není vždy možné, obecně se za třetí faktor považuje „rozklad LUP“ s permutační maticí .
Nejběžnější typy maticových faktorizací najdete v části Rozklad matice.
Logické matice reprezentuje binární relaci , a maticové násobení odpovídá složení vztahů . Dekompozice vztahu prostřednictvím faktorizace slouží k profilování povahy vztahu, jako je například difunkční vztah.
Viz také
- Eulerova faktorizační metoda pro celá čísla
- Fermatova faktorizační metoda pro celá čísla
- Monoidní faktorizace
- Multiplikativní oddíl
- Tabulka Gaussových celočíselných faktorizací
Poznámky
Reference
- Burnside, William Snow ; Panton, Arthur William (1960) [1912], Teorie rovnic s úvodem do teorie binárních algebraických forem (svazek první) , Dover
- Dickson, Leonard Eugene (1922), první kurz teorie rovnic , New York: John Wiley & Sons
- Fite, William Benjamin (1921), College Algebra (revidovaný) , Boston: DC Heath & Co.
- Klein, Felix (1925), Elementární matematika z pokročilého hlediska; Aritmetika, algebra, analýza , Dover
- Selby, Samuel M., CRC Standard Mathematical Tables (18. vydání.), The Chemical Rubber Co.

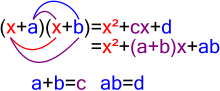






























































































































![\ mathbb {Z} [{\ sqrt {-5}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/643ef2c1e3b8b8e684a0ddf73d649cb0202cc0c1)
