Iterace s pevným bodem - Fixed-point iteration

V numerické analýze , s pevnou řádovou čárkou iterační je způsob výpočtu pevných bodů funkce.

Přesněji řečeno, vzhledem k tomu, funkce definované na základě reálných čísel se skutečnými hodnotami a daný bod v doméně z je s pevnou řádovou čárkou iterace ${\ displaystyle f}$ ${\ displaystyle x_ {0}}$ ${\ displaystyle f}$

{\ displaystyle x_ {n + 1} = f (x_ {n}), \, n = 0,1,2, \ tečky}

což vede k posloupnosti, u které se doufá, že konverguje k bodu . Pokud je spojitý, pak lze dokázat, že získaný je pevný bod , tj. ${\ displaystyle x_ {0}, x_ {1}, x_ {2}, \ dots}$ ${\ displaystyle x}$ ${\ displaystyle f}$ ${\ displaystyle x}$ ${\ displaystyle f}$

{\ displaystyle f (x) = x. \,}

Obecněji lze funkci definovat v jakémkoli metrickém prostoru s hodnotami ve stejném prostoru. ${\ displaystyle f}$

Příklady

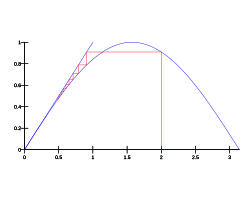
První jednoduché a užitečné příkladem je babylonský metoda pro výpočet druhé odmocniny z > 0, který spočívá v tom , tedy střední hodnota x a / X , přiblížit k hranici (z jakéhokoli výchozího bodu ). Toto je zvláštní případ níže uvedené Newtonovy metody . ${\ displaystyle f (x) = {\ frac {1} {2}} \ vlevo ({\ frac {a} {x}} + x \ vpravo)}$ ${\ displaystyle x = {\ sqrt {a}}}$ ${\ displaystyle x_ {0} \ gg 0}$

Iterace s pevným bodem x _{n +1} = sin x _n s počáteční hodnotou x ₀ = 2 konverguje k 0. Tento příklad nesplňuje předpoklady Banachovy věty o pevném bodě, a proto je jeho rychlost konvergence velmi pomalá.

Iterace s pevným bodem konverguje k jedinečnému pevnému bodu funkce pro libovolný počáteční bod. Tento příklad splňuje předpoklady Banachovy věty o pevném bodě . Proto chyba po n krocích splňuje (kde můžeme vzít , pokud začneme od .) Když je chyba menší než násobek nějaké konstanty q , řekneme, že máme lineární konvergenci . Banachova věta o pevném bodě umožňuje jednomu získat iterace s pevným bodem s lineární konvergencí. ${\ displaystyle x_ {n + 1} = \ cos x_ {n} \,}$ ${\ displaystyle f (x) = \ cos x \,}$ ${\ displaystyle x_ {0}.}$ ${\ displaystyle | x_ {n} -x | \ leq {q ^ {n} \ nad 1-q} | x_ {1} -x_ {0} | = Cq ^ {n}}$ ${\ displaystyle q = 0,85}$ ${\ displaystyle x_ {0} = 1}$ ${\ displaystyle q ^ {n}}$
Iterace s pevným bodem se bude lišit, pokud . Říkáme, že pevný bod je odpuzující. ${\ displaystyle x_ {n + 1} = 2x_ {n} \,}$ ${\ displaystyle x_ {0} = 0}$ ${\ displaystyle f (x) = 2x \,}$
Požadavek, že f je spojitý, je důležitý, jak ukazuje následující příklad. Iterace ${\ displaystyle x_ {n + 1} = {\ begin {cases} {\ frac {x_ {n}} {2}}, & x_ {n} \ neq 0 \\ 1, & x_ {n} = 0 \ end { případy}}}$ konverguje na 0 pro všechny hodnoty . 0 však není pevným bodem funkce ${\ displaystyle x_ {0}}$ ${\ displaystyle f (x) = {\ begin {cases} {\ frac {x} {2}}, & x \ neq 0 \\ 1, & x = 0 \ end {cases}}}$ protože tato funkce není spojitá v , a ve skutečnosti nemá žádné pevné body. ${\ displaystyle x = 0}$

Aplikace

Newtonova metoda pro nalezení kořenů dané diferencovatelné funkce je ${\ displaystyle f (x)}$ ${\ textstyle x_ {n + 1} = x_ {n} - {\ frac {f (x_ {n})} {f '(x_ {n})}}.}$
Pokud píšeme , můžeme přepsat Newtonovu iteraci jako iteraci s pevným bodem . ${\ textstyle g (x) = x - {\ frac {f (x)} {f '(x)}}}$ ${\ textstyle x_ {n + 1} = g (x_ {n})}$

Pokud Tato iterace konverguje k pevnému bodu $x$ o $g$ , tedy tak, ${\ textstyle x = g (x) = x - {\ frac {f (x)} {f '(x)}}}$ ${\ textstyle f (x) / f '(x) = 0.}$
Reciproční čehokoli je nenulová, tedy $f (x) = 0$ : $x$ je kořen z $f$ . Na základě předpokladů Banachovy věty o pevném bodě Newtonova iterace, zarámovaná jako metoda s pevným bodem, demonstruje lineární konvergenci . Podrobnější analýza však ukazuje kvadratickou konvergenci , tj. Za určitých okolností. ${\ textstyle | x_ {n} -x | <Cq ^ {2 ^ {n}}}$
Halleyova metoda je obdobou Newtonovy metody, když funguje správně, ale její chyba je ( kubická konvergence ). Obecně je možné navrhnout metody, které konvergují s rychlostí pro všechny . Obecně platí, že čím vyšší $k$ , tím méně stabilní a výpočetně dražší. Z těchto důvodů se metody vyššího řádu obvykle nepoužívají. ${\ displaystyle | x_ {n} -x | <Cq ^ {3 ^ {n}}}$ ${\ displaystyle Cq ^ {k ^ {n}}}$ ${\ displaystyle k \ in \ mathbb {N}}$
Metody Runge – Kutta a numerické běžné řešení diferenciálních rovnic obecně lze považovat za iterace s pevným bodem. Základní myšlenkou při analýze A-stability řešení ODE je začít se zvláštním případem , kde je komplexní číslo , a zkontrolovat, zda řešení ODE konverguje do pevného bodu, kdykoli je jeho skutečná část záporná. ${\ displaystyle y '= ay}$ ${\ displaystyle a}$ ${\ displaystyle y = 0}$ ${\ displaystyle a}$
Picard-Lindelöf věta , která ukazuje, že obyčejné diferenciální rovnice má řešení, je v podstatě aplikace Banachových s pevnou řádovou čárkou teorém zvláštního sledu funkcí, které tvoří pevné bodu iteraci, konstrukci řešení rovnice. Řešení ODR tímto způsobem se nazývá Picardova iterace , Picardova metoda nebo Picardův iterační proces .
Schopnost iterace v aplikaci Excel lze použít k nalezení řešení Colebrookovy rovnice s přesností na 15 platných čísel.
Některá schémata „postupné aproximace“ používaná v dynamickém programování k řešení Bellmanovy funkční rovnice jsou založena na iteracích s pevným bodem v prostoru návratové funkce.

Kontrakce

Pokud je funkce definovaná na reálné linii se skutečnými hodnotami Lipschitzova spojitá s Lipschitzovou konstantou , pak má tato funkce přesně jeden pevný bod a iterace pevného bodu konverguje k tomuto pevnému bodu pro jakýkoli počáteční odhad. Tuto větu lze zobecnit na jakýkoli úplný metrický prostor. ${\ displaystyle f}$ ${\ displaystyle L <1}$ ${\ displaystyle x_ {0}.}$

Důkaz této věty:

Jelikož je Lipschitzova spojitost s Lipschitzovou konstantou , pak pro sekvenci máme: ${\ displaystyle f}$ ${\ displaystyle L <1}$ ${\ displaystyle \ {x_ {n}, n = 0,1,2, \ ldots \}}$

{\ displaystyle {\ begin {aligned} | x_ {2} -x_ {1} | = | f (x_ {1}) - f (x_ {0}) | & \ leq L | x_ {1} -x_ { 0} |, \\ | x_ {3} -x_ {2} | = | f (x_ {2}) - f (x_ {1}) | & \ leq L | x_ {2} -x_ {1} | , \\ & \, \, \, \ vdots \ \ \ {\ text {and}} \\ | x_ {n} -x_ {n-1} | = | f (x_ {n-1}) - f (x_ {n-2}) | & \ leq L | x_ {n-1} -x_ {n-2} |. \ end {zarovnáno}}}

Kombinace výše uvedených nerovností přináší:

{\ displaystyle | x_ {n} -x_ {n-1} | \ leq L ^ {n-1} | x_ {1} -x_ {0} |.}

Protože , jak ${\ displaystyle L <1}$ ${\ displaystyle L ^ {n-1} \ rightarrow 0}$ ${\ displaystyle n \ rightarrow \ infty.}$

Můžeme tedy ukázat, že jde o Cauchyovu posloupnost, a tedy konverguje k bodu . ${\ displaystyle \ {x_ {n} \}}$ ${\ displaystyle x ^ {*}}$

Pro iteraci necháme jít do nekonečna na obou stranách rovnice, kterou získáme . To ukazuje, že je to pevný bod pro . Dokázali jsme tedy, že iterace nakonec konverguje k pevnému bodu. ${\ displaystyle x_ {n} = f (x_ {n-1})}$ ${\ displaystyle n}$ ${\ displaystyle x ^ {*} = f (x ^ {*})}$ ${\ displaystyle x ^ {*}}$ ${\ displaystyle f}$

Tato vlastnost je velmi užitečná, protože ne všechny iterace mohou dospět ke konvergentnímu pevnému bodu. Při konstrukci iterace s pevným bodem je velmi důležité zajistit, aby konvergovala. Existuje několik vět s pevným bodem, které zaručují existenci pevného bodu, ale protože iterační funkce je spojitá, můžeme obvykle použít výše uvedenou větu k otestování, zda iterace konverguje nebo ne. Důkaz zobecněné věty o dokončení metrických prostorů je podobný.

Zrychlení konvergence

Rychlost konvergence iterační sekvence lze zvýšit pomocí metody zrychlení konvergence, jako je Aitkenův delta-kvadrát proces . Aplikace Aitkenovy metody na iteraci s pevným bodem je známá jako Steffensenova metoda a lze ukázat, že Steffensenova metoda přináší míru konvergence, která je přinejmenším kvadratická.

Viz také

Reference

Další čtení

Burden, Richard L .; Faires, J. Douglas (1985). "Iterace s pevným bodem". Numerická analýza (třetí vydání). Vydavatelé PWS. ISBN 0-87150-857-5.
Hoffman, Joe D .; Frankel, Steven (2001). "Iterace s pevným bodem" . Numerické metody pro inženýry a vědce (druhé vydání). New York: CRC Press. str. 141–145. ISBN 0-8247-0443-6.
Judd, Kenneth L. (1998). "Iterace s pevným bodem" . Numerické metody v ekonomii . Cambridge: MIT Press. str. 165–167. ISBN 0-262-10071-1.

Languages

In other projects