Mechanika třecího kontaktu - Frictional contact mechanics

Část série na
Mechanika kontinua
:${\ Displaystyle J = -D {\ frac {d \ varphi} {dx}}}$ Fickovy zákony difúze
Zákony Konzervace Hmotnost Hybnost Energie Nerovnosti Clausius – Duhem (entropie)
Pevná mechanika Deformace Pružnost lineární Plasticita Hookův zákon Stres Konečné napětí Nekonečně malé napětí Kompatibilita Ohýbání Kontaktujte mechaniky třecí Teorie selhání materiálu Mechanika lomu
Mechanika tekutin Kapaliny Statika  · Dynamika Archimédův princip  · Bernoulliho princip Navier – Stokesovy rovnice Poiseuilleova rovnice  · Pascalův zákon Viskozita ( Newtonský  · nenewtonský ) Vztlak  · Míchání  · Tlak Kapaliny Povrchové napětí Kapilární akce Plyny Atmosféra Boyleův zákon Charlesův zákon Kombinovaný plynový zákon Fickův zákon Gay-Lussacov zákon Grahamův zákon Plazma
Reologie Viskoelasticita Reometrie Reometr Chytré tekutiny Elektrorheologické Magnetoreologické Ferrofluidy
Vědci Bernoulli Boyle Cauchy Charlesi Euler Fick Gay-Lussac Grahame Hooke Newton Navier Noll Pascal Stokes Truesdell
proti t E

Kontaktní mechanika je studie o deformaci z pevných látek , které se dotýkají navzájem v jednom nebo více bodech. To lze rozdělit na tlakové a adhezivní síly ve směru kolmém na rozhraní a třecí síly v tangenciálním směru. Mechanika třecího kontaktu je studium deformace těles za přítomnosti třecích účinků, zatímco mechanika bez tření předpokládá nepřítomnost takových účinků.

Mechanika třecího kontaktu se zabývá velkým rozsahem různých měřítek.

• V makroskopickém měřítku se používá pro zkoumání pohybu kontaktních těles (viz Kontaktní dynamika ). Například odraz gumové koule na povrch závisí na třecí interakci na kontaktním rozhraní. Zde je hlavním problémem celková síla versus odsazení a boční posun.
• V mezilehlém měřítku se člověk zajímá o místní napětí , deformace a deformace kontaktních těles v kontaktní oblasti a v její blízkosti. Například odvozovat nebo ověřovat kontaktní modely v makroskopickém měřítku nebo zkoumat opotřebení a poškození povrchů kontaktujících těl. Oblasti použití v tomto měřítku jsou interakce vozovky s pneumatikami, interakce železničního kola s kolejnicí, analýza válečkových ložisek atd.
• Konečně, v mikroskopických a nanorozsahech se kontaktní mechanika používá k lepšímu porozumění tribologickým systémům (např. Zkoumá původ tření ) a pro konstrukci pokročilých zařízení, jako jsou mikroskopy atomových sil a zařízení MEMS .

Tato stránka se zabývá především druhou škálou: získání základního vhledu do napětí a deformací v kontaktní ploše a poblíž ní, aniž by se příliš věnovala podrobným mechanismům, díky nimž vznikají.

Dějiny

K pochopení tření přispělo několik slavných vědců, inženýrů a matematiků. Patří mezi ně Leonardo da Vinci , Guillaume Amontons , John Theophilus Desaguliers , Leonhard Euler a Charles-Augustin de Coulomb . Později Nikolai Pavlovič Petrov , Osborne Reynolds a Richard Stribeck toto chápání doplnili teoriemi mazání .

Deformaci pevných materiálů zkoumali v 17. a 18. století Robert Hooke , Joseph Louis Lagrange a v 19. a 20. století d'Alembert a Timoshenko . Pokud jde o kontaktní mechaniku, vyniká klasický přínos Heinricha Hertze . Dále zásadní řešení Boussinesq a Cerruti mají primární význam pro zkoumání problémů s třecím kontaktem v (lineárně) elastickém režimu.

V železničních aplikacích je třeba znát vztah mezi dotvarováním (rozdílem rychlosti) a třecí silou .${\ displaystyle \ xi}$${\ displaystyle F_ {w}}$

Klasické výsledky skutečného problému s třecím kontaktem se týkají papírů FW Cartera (1926) a H. Fromma (1927). Nezávisle prezentovali vztah dotvarování a dotvarování síly pro válec v rovině nebo pro dva válce v ustáleném valivém kontaktu pomocí Coulombova zákona o suchém tření (viz níže). Ty jsou aplikovány na trakci železniční lokomotivy a pro pochopení lovecké oscilace železničních vozidel. Pokud jde o klouzání, za klasická řešení stojí C. Cattaneo (1938) a RD Mindlin (1949), kteří uvažovali o tangenciálním posunutí koule v rovině (viz níže).

V 50. letech vzrostl zájem o valivý kontakt železničních kol. V roce 1958 Kenneth L. Johnson představil přibližný přístup k 3D třecímu problému s Hertzianovou geometrií, s bočním nebo spinovým dotvarováním. Mimo jiné zjistil, že dotvarování rotace, které je symetrické ke středu kontaktní plochy, vede k valivé boční síle v podmínkách odvalování. To je způsobeno rozdíly mezi rozdělením tahů v kontaktní ploše dopředu a dozadu.

V roce 1967 publikoval Joost Jacques Kalker svou milníkovou disertační práci na téma lineární teorie pro valivý kontakt. Tato teorie je přesná pro situaci koeficientu nekonečného tření, v takovém případě oblast skluzu zmizí, a je přibližná pro nemizející dotvarování. Předpokládá Coulombův třecí zákon, který víceméně vyžaduje (úzkostlivě) čisté povrchy. Tato teorie je pro masivní tělesa, jako je železniční kolo-kolejový kontakt. Pokud jde o interakci mezi silnicí a pneumatikou, důležitý příspěvek se týká takzvané magické formule pneumatiky od Hanse Pacejky .

V sedmdesátých letech bylo navrženo mnoho numerických modelů. Zvláště variační přístupy , jako jsou ty, které se opírají o Duvautovu a Lionovu existenci a teorie jedinečnosti. Postupem času tyto přerostly do přístupů konečných prvků pro kontaktní problémy s obecnými materiálovými modely a geometriemi a do přístupů založených na polovičním prostoru pro takzvané problémy s hladkými hranami pro lineárně elastické materiály. Modely první kategorie představili Laursen a Wriggers. Příkladem druhé kategorie je model Kalker's CONTACT.

Nevýhodou dobře podložených variačních přístupů je jejich velká doba výpočtu. Proto bylo také navrženo mnoho různých přibližných přístupů. Několik známých přibližných teorií pro problém valivého kontaktu je Kalkerův přístup FASTSIM, Shen-Hedrick-Elkinsův vzorec a Polachův přístup.

Další informace o historii problému s kontaktem kola/kolejnice jsou uvedeny v Knotheho příspěvku. Dále Johnson ve své knize shromáždil obrovské množství informací o kontaktní mechanice a souvisejících předmětech. S ohledem na mechaniku valivých kontaktů uvádí Kalker také přehled různých teorií. Zajímavé jsou nakonec kurzy CISM, které poskytují úvod do pokročilejších aspektů teorie valivých kontaktů.

Formulace problému

Ústředním bodem analýzy problémů s třecím kontaktem je pochopení toho, že napětí na povrchu každého tělesa se prostorově mění. V důsledku toho se napětí a deformace těl mění také podle polohy. A pohyb částic kontaktních těles se může na různých místech lišit: v části kontaktních ploch mohou částice protilehlých těl k sobě přilnout (držet), zatímco v jiných částech kontaktní plochy dochází k relativnímu pohybu. Tato místní relativní klouzání se nazývá mikro- skluz .

Toto rozdělení kontaktní oblasti na tyčovou (adhezní) a kluzkou oblast se projevuje mimo jiné třením . Všimněte si, že opotřebení dochází pouze tehdy, pokud výkon je rozptýlena, což vyžaduje stres a místní relativní posunutí (skluz) mezi dvěma povrchy.

Velikost a tvar samotné kontaktní plochy a jejích adhezních a kluzných oblastí jsou obecně předem neznámé. Pokud by to byly známy, pak by elastická pole v těchto dvou tělech mohla být řešena nezávisle na sobě a problém by již nebyl problémem kontaktu.

V problému s kontaktem lze rozlišit tři různé součásti.

1. Především jde o deformaci jednotlivých těles v reakci na zatížení působící na jejich povrchy. Toto je předmětem obecné mechaniky kontinua . To do značné míry závisí na geometrii těles a na jejich ( konstitutivním ) materiálovém chování (např. Pružná vs. plastická reakce, homogenní vs. vrstvená struktura atd.).
2. Za druhé, existuje celkový pohyb těl vůči sobě navzájem. Například tělesa mohou být v klidu (statika), nebo k sobě přibližují rychle ( dopad ), a může být posunut (posuvné) nebo otáčet ( válcování ) přes sebe. Tyto celkové pohyby jsou obecně studovány v klasické mechanice , viz například dynamika více těl .
3. Nakonec existují procesy na kontaktním rozhraní : stlačení a přilnavost ve směru kolmém na rozhraní a tření a mikro skluz v tangenciálních směrech .

Poslední aspekt je hlavní starostí kontaktní mechaniky. Je popsán z hlediska takzvaných kontaktních podmínek . Pro směr kolmý na rozhraní, normální kontaktní problém, jsou účinky adheze obvykle malé (ve větších prostorových měřítcích) a obvykle se používají následující podmínky:

1. Mezera mezi dvěma povrchy musí být nulová (kontaktní) nebo přísně kladná (separace, );${\ displaystyle e_ {n}}$${\ displaystyle e_ {n}> 0}$
2. Normální napětí působící na každé těleso je nulové (separace) nebo tlakové ( v kontaktu).${\ displaystyle p_ {n}}$${\ displaystyle p_ {n}> 0}$

Matematicky: . Zde jsou funkce, které se liší podle polohy podél povrchů těl. ${\ Displaystyle e_ {n} \ geq 0, p_ {n} \ geq 0, e_ {n} \ cdot p_ {n} = 0 \, \!}$${\ displaystyle e_ {n}, p_ {n}}$

V tangenciálních směrech se často používají následující podmínky:

1. Místní (tangenciální) smykové napětí (za předpokladu normálního směru rovnoběžného s -osou) nesmí překročit určité maximum závislé na poloze, takzvanou trakční mez ;${\ displaystyle {\ vec {p}} = (p_ {x}, p_ {y})^{\ mathsf {T}} \, \!}$${\ Displaystyle z}$${\ displaystyle g}$
2. Tam, kde velikost tangenciální trakce klesne pod hranici trakce , se protilehlé povrchy spojí a mikroklouz zmizí ;${\ Displaystyle \ | {\ vec {p}} \ | <g \, \!}$${\ Displaystyle {\ vec {s}} = (s_ {x}, s_ {y})^{\ mathsf {T}} = {\ vec {0}} \, \!}$
3. K mikroprokluzu dochází tam, kde jsou tangenciální tahy na hranici tahu; směr tangenciální trakce je pak opačný ke směru mikro skluzu .${\ displaystyle {\ vec {p}} =-g {\ vec {s}}/\ | {\ vec {s}} \ | \, \!}$

Přesnou formou vázané tahové síly je takzvaný zákon místního tření. Proto se Coulombův (globální) zákon o tření často používá lokálně: s koeficientem tření. Jsou také možné podrobnější vzorce, například v závislosti na teplotě , místní kluzné rychlosti atd. ${\ Displaystyle \ | {\ vec {p}} \ | \ leq g = \ mu p_ {n} \, \!}$${\ Displaystyle \ mu}$${\ Displaystyle \ mu}$${\ displaystyle T}$${\ displaystyle \ | {\ vec {s}} \ |}$

Řešení pro statické případy

Lano na patníku, capstanova rovnice

Ilustrace pružného lana omotaného kolem pevného předmětu, jako je sloupek. Kontaktní plocha je rozdělena na zónové a kluzné zóny v závislosti na zatížení působícím na oba konce a na historii zatížení.

Zvažte lano, kde na obě strany působí stejné síly (např. ). Tím se lano trochu natáhne a vyvolá vnitřní napětí ( v každé poloze podél lana). Lano je omotáno kolem pevného předmětu, jako je sloupek ; je ohnutý a dotýká se povrchu předmětu pod kontaktním úhlem (např. ). Mezi lanem a patníkem vzniká normální tlak, ale zatím nedochází k žádnému tření. Potom se síla na jedné straně patníku zvýší na vyšší hodnotu (např. ). To způsobí třecí smyková napětí v kontaktní oblasti. V konečné situaci patník vyvíjí třecí sílu na lano tak, aby došlo ke statické situaci. ${\ displaystyle F _ {\ text {hold}} = 400 \, \ mathrm {N}}$ ${\ displaystyle T}$${\ Displaystyle T = 400 \, \ mathrm {N}}$${\ displaystyle 180^{\ circ}}$${\ displaystyle F _ {\ text {load}} = 600 \, \ mathrm {N}}$

Rozložení tahu v laně v této konečné situaci je popsáno pomocí rovnice hřebenu s řešením:

${\ displaystyle {\ begin {aligned} T (\ phi) & = T _ {\ text {hold}}, & \ phi & \ in \ left [\ phi _ {\ text {hold}}, \ phi _ {\ text {intf}} \ right] \\ T (\ phi) & = T _ {\ text {load}} e^{-\ mu \ phi}, & \ phi & \ in \ left [\ phi _ {\ text {intf}}, \ phi _ {\ text {load}} \ right] \\\ phi _ {\ text {intf}} & = {\ frac {1} {\ mu}} \ log \ left ({\ frac {T _ {\ text {load}}} {T _ {\ text {hold}}}} \ right) & \ end {aligned}}}$

Napětí se zvyšuje z uvolněné strany ( ) na vysokou stranu . Při pohledu z vyšší strany napětí exponenciálně klesá, dokud nedosáhne nižšího zatížení při . Odtud je na této hodnotě konstantní. Přechodový bod je určen poměrem obou zatížení a součinitelem tření. Zde je napětí v Newtonech a úhly v radiánech. ${\ displaystyle T _ {\ text {hold}}}$${\ displaystyle \ phi = \ phi _ {\ text {hold}}}$${\ displaystyle T _ {\ text {load}}}$${\ displaystyle \ phi = \ phi _ {\ text {load}}}$${\ displaystyle \ phi = \ phi _ {\ text {intf}}}$${\ displaystyle \ phi _ {\ text {intf}}}$${\ displaystyle T}$${\ displaystyle \ phi}$

Napětí v laně v konečné situaci se zvyšuje s ohledem na počáteční stav. Proto se lano trochu prodlouží. To znamená, že ne všechny povrchové částice lana mohly držet svou počáteční polohu na povrchu sloupku. Během nakládacího procesu lano trochu uklouzlo po povrchu patníku v oblasti skluzu . Tento skluz je dostatečně velký, aby se dostal k prodloužení, ke kterému dochází v konečném stavu. Všimněte si, že v konečném stavu nedochází k žádnému uklouznutí; termín smyková oblast se vztahuje na uklouznutí, ke kterému došlo během procesu načítání. Dále si všimněte, že umístění oblasti skluzu závisí na počátečním stavu a procesu načítání. Pokud je počáteční napětí a napětí se sníží na na uvolněné straně, pak klouzavá oblast nastane na uvolněné straně kontaktní oblasti. Pro počáteční napětí mezi a mohou být na obou stranách kluzné oblasti s mezerou mezi nimi. ${\ displaystyle T}$ ${\ displaystyle \ phi \ in [\ phi _ {\ text {intf}}, \ phi _ {\ text {load}}]}}$${\ displaystyle 600 \, \ mathrm {N}}$${\ displaystyle 400 \, \ mathrm {N}}$${\ displaystyle 400}$${\ displaystyle 600 \, \ mathrm {N}}$

Zobecnění pro lano ležící na libovolném ortotropním povrchu

Pokud lano leží v rovnováze za tangenciálních sil na drsném ortotropním povrchu, pak jsou splněny tři následující podmínky (všechny):

Tuto generalizaci získal Konyukhov A.,

Koule v letadle, (3D) problém Cattaneo

Uvažujme kouli, která je přitlačena na rovinu (poloviční prostor) a poté posunuta po povrchu roviny. Pokud jsou koule a rovina idealizovány jako tuhá tělesa, pak by ke kontaktu došlo pouze v jednom bodě a koule by se nepohybovala, dokud aplikovaná tangenciální síla nedosáhne maximální třecí síly. Poté začne klouzat po povrchu, dokud se aplikovaná síla opět nesníží.

Ve skutečnosti, s ohledem na elastické efekty, je situace velmi odlišná. Pokud je elastická koule přitlačena na elastickou rovinu ze stejného materiálu, pak se obě tělesa deformují, vznikne kruhová kontaktní oblast a vznikne (Hertzianovo) normální rozložení tlaku. Střed koule se posune dolů o vzdálenost nazývanou přiblížení , která je ekvivalentní maximálnímu průniku nedeformovaných povrchů. Pro sféru poloměru a elastických konstant toto Hertzianovo řešení zní: ${\ displaystyle \ delta _ {n}}$${\ displaystyle R}$${\ Displaystyle E, \ nu}$

${\ displaystyle {\ begin {aligned} p_ {n} (x, y) & = p_ {0} {\ sqrt {1-{\ frac {r^{2}} {a^{2}}}}} & r & = {\ sqrt {x^{2}+y^{2}}} \ leq a & a & = {\ sqrt {R \ delta _ {n}}} \\ p_ {0} & = {\ frac {2} {\ pi}} E^{*} {\ sqrt {\ frac {\ delta _ {n}} {R}}} & F_ {n} & = {\ frac {4} {3}} E^{*} {\ sqrt {R}} \ delta _ {n}^{\ frac {3} {2}} & E^{*} & = {\ frac {E} {2 \ left (1- \ nu^{2} \ right)}} \ end {aligned}}}$

Nyní zvažte, že je použita tangenciální síla, která je nižší než vazba Coulombova tření . Střed koule se pak posune do strany o malou vzdálenost, která se nazývá posun . Získá se statická rovnováha, ve které dochází k elastickým deformacím a také třecím smykovým napětím v kontaktním rozhraní. V tomto případě, pokud je tangenciální síla snížena, pak se sníží také pružné deformace a smyková napětí. Koule se do značné míry posune zpět do své původní polohy, s výjimkou ztrát třením, které vznikají v důsledku lokálního skluzu v kontaktní ploše. ${\ displaystyle F_ {x}}$${\ displaystyle \ mu F_ {n}}$${\ displaystyle \ delta _ {x}}$

Tento problém s kontaktem vyřešil přibližně Cattaneo pomocí analytického přístupu. Rozložení napětí v rovnovážném stavu se skládá ze dvou částí:

${\ Displaystyle {\ begin {aligned} p_ {x} (x, y) & = \ mu p_ {0} \ left ({\ sqrt {1-{\ frac {r^{2}} {a^{2 }}}}}-{\ frac {c} {a}} {\ sqrt {1-{\ frac {r^{2}} {c^{2}}}}} \ right) & 0 \ leq {} & r \ leq c \\ p_ {x} (x, y) & = \ mu p_ {n} (x, y) & c \ leq {} & r \ leq a \\ p_ {x} (x, y) & = 0 & a \ leq {} & r \ end {aligned}}}$

V centrální lepivé oblasti se povrchové částice letadla posunují doprava, zatímco povrchové částice koule se posunují doleva. Přestože se koule jako celek pohybuje relativně vzhledem k rovině, tyto povrchové částice se vůči sobě nepohybovaly. Ve vnějším prstenci se povrchové částice pohybovaly vůči sobě navzájem. Jejich lokální posun je získán jako ${\ Displaystyle 0 \ leq r \ leq c}$${\ Displaystyle u_ {x} = \ delta _ {x}/2}$${\ Displaystyle u_ {x} =-\ delta _ {x}/2}$${\ displaystyle \ delta _ {x}}$${\ Displaystyle c \ leq r \ leq r}$

${\ Displaystyle s_ {x} (x, y) = \ delta _ {x}+u_ {x}^{\ text {sphere}} (x, y) -u_ {x}^{\ text {plane}} (x, y)}$

Tento posun je přesně tak velký, že je získána statická rovnováha se smykovým napětím na tahu vázaném v této takzvané smykové oblasti. ${\ displaystyle s_ {x} (x, y)}$

Během tangenciálního zatížení koule tedy dochází k částečnému sklouznutí . Kontaktní oblast je tedy rozdělena na kluznou oblast, kde se povrchy pohybují vůči sobě navzájem, a na oblast palice, kde se nepohybují. V rovnovážném stavu již žádné klouzání neprobíhá.

Řešení pro problémy s dynamickým klouzáním

Řešení problému s kontaktem se skládá ze stavu na rozhraní (kde je kontakt, rozdělení kontaktní plochy na tyčové a kluzné zóny a rozdělení normálového a smykového napětí) plus elastické pole v interiérech těles. Toto řešení závisí na historii kontaktu. To lze vidět rozšířením výše popsaného problému Cattaneo.

• V problému Cattaneo je koule nejprve přitlačena na rovinu a poté tangenciálně posunuta. Tím se získá částečný skluz, jak je popsáno výše.
• Pokud je koule nejprve tangenciálně posunuta a poté přitlačena na rovinu, pak mezi protilehlými plochami není žádný rozdíl tangenciálního posunutí a v důsledku toho v dotykovém rozhraní neexistuje tangenciální napětí.
• Pokud se přiblížení v normálním směru a tangenciální posun zvýší současně ("šikmá komprese"), pak lze situace dosáhnout tangenciálním napětím, ale bez lokálního skluzu.

To ukazuje, že stav v kontaktním rozhraní nezávisí pouze na relativních polohách obou těles, ale také na jejich historii pohybu. Další příklad toho nastane, pokud je koule posunuta zpět do své původní polohy. Zpočátku nebylo v dotykovém rozhraní žádné tangenciální napětí. Po počátečním posunu došlo k mikroprokluzu. Toto mikro sklouznutí není zcela vráceno posunutím zpět. V konečné situaci tedy tangenciální napětí zůstávají v rozhraní, což vypadá jako identická konfigurace jako původní.

Vliv tření na dynamické kontakty (nárazy) je podrobně zvažován v.

Řešení problémů s valivým kontaktem

Valivý kontakt mezi válcem a rovinou. Částice se pohybují v kontaktní oblasti zprava doleva a jsou stále více namáhány, dokud se nezaskočí místní klouzání.

Problémy s valivým kontaktem jsou dynamické problémy, ve kterých se kontaktní tělesa vůči sobě neustále pohybují. Rozdíl oproti problémům s dynamickým kluzným kontaktem je ten, že existuje větší rozmanitost ve stavu různých povrchových částic. Zatímco kontaktní plocha u klouzavého problému kontinuálně sestává z více či méně stejných částic, u problému s valivým kontaktem částice vstupují a opouštějí kontaktní plochu bez ustání. Navíc při klouzavém problému jsou povrchové částice v kontaktní ploše všude vystaveny víceméně stejnému tangenciálnímu posunu, zatímco při problému s válcováním jsou povrchové částice namáhány poměrně odlišnými způsoby. Jsou bez stresu při vstupu do kontaktní plochy, poté se přilepí na částici protilehlé plochy, jsou napjaty celkovým pohybovým rozdílem mezi těmito dvěma tělesy, dokud není překročena místní hranice tahu a nezačne se místní skluz. Tento proces je různé fáze pro různé části kontaktní oblasti.

Pokud je celkový pohyb těl konstantní, pak lze dosáhnout celkového ustáleného stavu. Zde se stav každé povrchové částice mění v čase, ale celkové rozdělení může být konstantní. To je formalizováno pomocí souřadnicového systému, který se pohybuje spolu s kontaktní plochou.

Válec valící se v rovině, (2D) řešení Carter-Fromm

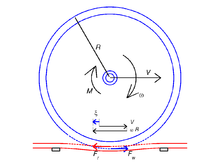
Zvažte válec, který se valí po rovině (polovičním prostoru) za stabilních podmínek, s časově nezávislým podélným dotvarováním . (Relativně) daleko od konců válců nastává situace rovinného napětí a problém je dvourozměrný. ${\ displaystyle \ xi}$

Pokud válec a rovina sestávají ze stejných materiálů, pak normální kontaktní problém není ovlivněn smykovým napětím. Kontaktní oblastí je proužek a tlak je popsán (2D) Hertzovým roztokem. ${\ Displaystyle x \ v [-a, a]}$

${\ displaystyle {\ begin {aligned} p_ {n} (x) & = {\ frac {p_ {0}} {a}} {\ sqrt {a^{2} -x^{2}}} & | x | & \ leq a & a^{2} & = {\ frac {4F_ {n} R} {\ pi E^{*}}} \\ p_ {0} & = {\ frac {2F_ {n}} { \ pi a}} &&& E ^{*} & = {\ frac {E} {2 \ left (1- \ nu ^{2} \ right)}} & \ end {aligned}}}$

Rozložení smykového napětí je popsáno v řešení Carter-Fromm. Skládá se z adhezní oblasti na náběžné hraně kontaktní oblasti a kluzné oblasti na zadní hraně. Je označena délka oblasti adheze . Souřadnice adheze je dále zavedena pomocí . V případě kladné síly (záporné dotvarování ) je to: ${\ displaystyle 2a '}$${\ displaystyle x '= x+a-a'}}$${\ displaystyle F_ {x}> 0}$${\ displaystyle \ xi <0}$

${\ Displaystyle {\ begin {aligned} p_ {x} (x) & = 0 & | & x | \ geq a \\ p_ {x} (x) & = {\ frac {\ mu p_ {0}} {a} } \ left ({\ sqrt {a^{2} -x^{2}}}-{\ sqrt {a '^{2} -x'^{2}}} \ right) & a-2a '\ leq {} & x \ leq a \\ p_ {x} (x) & = \ mu p_ {n} (x) && x \ leq a-2a '\ end {zarovnáno}}}$

Velikost oblasti adheze závisí na dotvarování, poloměru kola a součiniteli tření.

${\ displaystyle {\ begin {aligned} a '& = a {\ sqrt {1-{\ frac {| F_ {x} |} {\ mu F_ {n}}}}}, & {\ mbox {for} } | F_ {x} | \ leq \ mu F_ {n} \\\ xi & =-\ operatorname {sign} (F_ {x}) \, {\ frac {\ mu (a-a ')} R }}, & {\ mbox {ie}} | \ xi | \ leq {\ frac {\ mu a} {R}} \\ F_ {x} & =-\ operatorname {sign} (\ xi) \, \ mu F_ {n} \ left (1- \ left (1+{\ frac {R | \ xi |} {\ mu a}} \ right)^{2} \ right) \ end {aligned}}}$

U větších dotvarování tak, že dochází k úplnému sklouznutí. ${\ displaystyle a '= 0}$

Přístupy založené na polovičním prostoru

Při zvažování kontaktních problémů v mezilehlých prostorových měřítcích jsou nehomogenity drobného materiálu a drsnost povrchu ignorovány. Tělesa jsou považována za těla sestávající z hladkých povrchů a homogenních materiálů. Je použit přístup kontinua, kde jsou napětí, deformace a posuny popsány (po částech) spojitými funkcemi.

Polovina prostoru přístup je elegantním řešením strategie pro takzvané „hladkými okraji“ nebo „koncentrované“ kontaktních úloh.

1. Pokud je na malé části jeho povrchu zatíženo masivní elastické tělo, pak se elastická napětí zeslabují úměrně a elastická posunutí, když se člověk vzdálí od této povrchové oblasti.${\ Displaystyle 1/vzdálenost^{2}}$${\ Displaystyle 1/vzdálenost}$
2. Pokud těleso nemá v kontaktní oblasti nebo v její blízkosti žádné ostré rohy, pak její reakci na povrchové zatížení lze dobře aproximovat reakcí pružného půlprostoru (např. Všechny body s ).${\ Displaystyle (x, y, z) ^{\ mathsf {T}} \ in \ mathbb {R} ^{3} \, \!}$${\ Displaystyle z> 0 \, \!}$
3. Problém pružného poloprostoru je řešen analyticky, viz řešení Boussinesq-Cerruti .
4. Vzhledem k lineárnosti tohoto přístupu může být superponováno více dílčích řešení.

Pomocí základního řešení pro poloviční prostor je problém plného 3D kontaktu redukován na 2D problém ohraničujících ploch těl.

K dalšímu zjednodušení dochází, pokud jsou obě tělesa „geometricky a elasticky stejná“. Obecně platí, že napětí uvnitř tělesa v jednom směru vyvolává posunutí i v kolmých směrech. V důsledku toho existuje interakce mezi normálním napětím a tangenciálními posuny v kontaktním problému a interakce mezi tangenciálním napětím a normálním posunem. Pokud však normální napětí v kontaktním rozhraní vyvolá stejná tangenciální posunutí v obou kontaktních tělesech, pak nedochází k relativnímu tangenciálnímu posunutí obou povrchů. V takovém případě jsou normální a tangenciální problémy s kontakty odděleny. Pokud tomu tak je, pak se obě těla nazývají kvazi-identická . K tomu dochází například v případě, že těla jsou zrcadlově symetrická vzhledem k kontaktní rovině a mají stejné elastické konstanty.

Klasická řešení založená na přístupu polovičního prostoru jsou:

1. Hertz vyřešil problém kontaktu v nepřítomnosti tření, pro jednoduchou geometrii (zakřivené povrchy s konstantními poloměry zakřivení).
2. Carter zvažoval valivý kontakt mezi válcem a rovinou, jak je popsáno výše. Pro tangenciální trakci je k dispozici kompletní analytické řešení.
3. Cattaneo uvažoval o stlačení a posunutí dvou sfér, jak bylo popsáno výše. Toto analytické řešení je přibližné. Ve skutečnosti dochází k malým tangenciálním tahům, které jsou ignorovány.${\ displaystyle p_ {y}}$

Viz také

Reference

externí odkazy

• [1] Životopis Prof.dr.ir. JJ Kalker (Delft University of Technology).
• [2] Kalker's Hertzian/non-Hertzian CONTACT software.