Gödelova věta o úplnosti - Gödel's completeness theorem

Vzorec ( ∀ x . R ( x , x )) → (∀ x ∃ y . R ( x , y )) platí ve všech strukturách (vlevo je zobrazeno pouze těch nejjednodušších 8). Podle Gödelova výsledku úplnosti tedy musí mít důkaz o přirozeném odpočtu (zobrazeno vpravo).

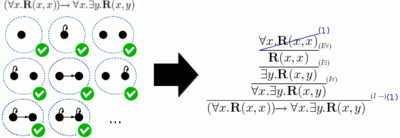
Gödelova věta o úplnosti je základní větou v matematické logice, která vytváří shodu mezi sémantickou pravdou a syntaktickou prokazatelností v logice prvního řádu .

Věta o úplnosti platí pro jakoukoli teorii prvního řádu : Pokud T je taková teorie a φ je věta (ve stejném jazyce) a jakýkoli model T je modelem φ, pak existuje důkaz (prvního řádu) φ pomocí příkazů T jako axiomů. Člověk to někdy říká jako „cokoli pravdivého je dokázatelné“.

Vytváří úzké spojení mezi modelovou teorií, která se zabývá tím, co je pravdivé v různých modelech, a teorií důkazů, která studuje, co lze formálně prokázat v konkrétních formálních systémech .

Poprvé to dokázal Kurt Gödel v roce 1929. Poté to bylo zjednodušeno v roce 1947, kdy Leon Henkin pozoroval ve své Ph.D. teze , že tvrdá část důkazu může být prezentována jako Modelová věta o existenci (publikováno v roce 1949). Henkinův důkaz zjednodušil Gisbert Hasenjaeger v roce 1953.

Předkola

Existuje mnoho deduktivních systémů pro logiku prvního řádu, včetně systémů přirozené dedukce a systémů ve stylu Hilberta . Společné pro všechny deduktivní systémy je pojem formální odpočet . Toto je posloupnost (nebo v některých případech konečný strom ) vzorců se speciálně určeným závěrem . Definice odpočtu je taková, že je konečná a že je možné algoritmicky ověřit (například počítačem nebo rukou), že daná posloupnost (nebo strom) vzorců je skutečně odpočtem.

Vzorec prvního řádu se nazývá logicky platný, pokud platí v každé struktuře pro jazyk vzorce (tj. Pro jakékoli přiřazování hodnot proměnným vzorce). Abychom formálně uvedli a poté dokázali větu úplnosti, je nutné definovat také deduktivní systém. Deduktivní systém se nazývá úplný, pokud je každý logicky platný vzorec závěrem nějaké formální dedukce a věta o úplnosti pro konkrétní deduktivní systém je věta, že je v tomto smyslu úplná. V určitém smyslu tedy pro každý deduktivní systém existuje jiná věta o úplnosti. Konverzací k úplnosti je zdravost , skutečnost, že v deduktivním systému jsou prokazatelné pouze logicky platné vzorce.

Pokud je nějaký konkrétní deduktivní systém logiky prvního řádu zdravý a úplný, pak je „dokonalý“ (vzorec je prokazatelný tehdy a jen tehdy, je-li logicky platný), tedy ekvivalentní jakémukoli jinému deduktivnímu systému se stejnou kvalitou (jakýkoli důkaz v jednom systému lze převést na druhý).

Tvrzení

Nejprve opravíme deduktivní systém predikátového počtu prvního řádu a vybereme některý ze známých ekvivalentních systémů. Gödelův původní důkaz předpokládal důkazní systém Hilbert-Ackermann.

Gödelova původní formulace

Věta o úplnosti říká, že pokud je vzorec logicky platný, pak existuje konečný odpočet (formální důkaz) vzorce.

Deduktivní systém je tedy „úplný“ v tom smyslu, že k prokázání všech logicky platných vzorců nejsou vyžadována žádná další odvozovací pravidla. Konverzací k úplnosti je zdravost , skutečnost, že v deduktivním systému jsou prokazatelné pouze logicky platné vzorce. Spolu se spolehlivostí (jejíž ověření je snadné) tato věta znamená, že vzorec je logicky platný tehdy a jen tehdy, pokud jde o uzavření formální dedukce.

Obecnější forma

Věta může být vyjádřena obecněji z hlediska logických důsledků . Říkáme, že věta s je syntaktickým důsledkem teorie T , označované , pokud je s v našem deduktivním systému prokazatelné z T. Říkáme, že to je sémantický důsledek of T , označil , pokud to má v každém modelu z T . Úplnosti teorém pak říká, že pro jakýkoli prvního řádu teorie T s dobře orderable jazyka a jakýkoli trest s jazykem T , ${\ Displaystyle T \ vdash s}$${\ Displaystyle T \ models s}$

když , tak .${\ Displaystyle T \ models s}$${\ Displaystyle T \ vdash s}$

Vzhledem k tomu, že platí i obrácení (zdravost), vyplývá, že pokud a pouze tehdy , a tedy že syntaktický a sémantický důsledek jsou ekvivalentní logice prvního řádu. ${\ Displaystyle T \ models s}$ ${\ Displaystyle T \ vdash s}$

Tato obecnější věta se používá implicitně, například když je věta ukázána jako prokazatelná z axiomů teorie grup zvážením libovolné skupiny a ukázáním, že věta je touto skupinou splněna.

Gödelova původní formulace je odvozena z konkrétního případu teorie bez jakéhokoli axiomu.

Modelová věta o existenci

Věta o úplnosti může být také chápána z hlediska konzistence , jako důsledek Henkinovy modelové věty o existenci . Říkáme, že teorie T je syntakticky konzistentní, pokud neexistuje věta s tak, že jak s, tak její negace ¬ s jsou prokazatelné z T v našem deduktivním systému. Věta o modelové existenci říká, že pro jakoukoli teorii prvního řádu T s dobře uspořádaným jazykem,

pokud je syntakticky konzistentní, pak má model.${\ displaystyle T}$${\ displaystyle T}$

Další verze s napojením na Löwenheim – Skolemovu větu říká:

Každá syntakticky konzistentní, počitatelná teorie prvního řádu má konečný nebo počitatelný model.

Vzhledem k Henkinově větě lze větu o úplnosti dokázat následovně: Pokud , pak nemá modely. Na rozdíl od Henkinovy ​​věty je pak syntakticky nekonzistentní. Takže rozpor ( ) je prokazatelný z v deduktivním systému. Z tohoto důvodu , a pak vlastnosti deduktivních systému . ${\ Displaystyle T \ models s}$${\ Displaystyle T \ cup \ lnot s}$${\ Displaystyle T \ cup \ lnot s}$${\ displaystyle \ bot}$${\ Displaystyle T \ cup \ lnot s}$${\ Displaystyle (T \ cup \ lnot s) \ vdash \ bot}$${\ Displaystyle T \ vdash s}$

Jako teorém aritmetiky

Modelovou větu o existenci a její důkaz lze formalizovat v rámci Peanoovy aritmetiky . Přesně můžeme systematicky definovat model jakékoli konzistentní efektivní teorie prvního řádu T v Peanoově aritmetice interpretací každého symbolu T pomocí aritmetického vzorce, jehož volné proměnné jsou argumenty symbolu. (V mnoha případech budeme muset jako hypotézu konstrukce předpokládat, že T je konzistentní, protože aritmetika Peano tuto skutečnost nemusí prokázat.) Definice vyjádřená tímto vzorcem však není rekurzivní (ale obecně je , Δ ₂ ).

Důsledky

Důležitým důsledkem věty o úplnosti je, že je možné rekurzivně vyjmenovat sémantické důsledky jakékoli efektivní teorie prvního řádu, vyjmenováním všech možných formálních dedukcí z axiomů teorie, a použít to k vytvoření výčtu jejich závěrů .

To je v kontrastu s přímým významem pojmu sémantický důsledek, který kvantifikuje všechny struktury v konkrétním jazyce, což zjevně není rekurzivní definice.

Také to činí koncept „prokazatelnosti“, a tedy „věty“, jasným konceptem, který závisí pouze na zvoleném systému axiomů teorie, a nikoli na volbě důkazního systému.

Vztah k větám o neúplnosti

Gödelovy věty o neúplnosti ukazují, že existují určitá omezení toho, co lze prokázat v jakékoli dané teorii prvního řádu v matematice. „Neúplnost“ v jejich názvu odkazuje na jiný význam úplnosti (viz teorie modelu - Použití vět o kompaktnosti a úplnosti ): Teorie je úplná (nebo rozhodnutelná), pokud je každá věta v jazyce buď prokazatelná ( ) nebo vyvratitelná ( ) . ${\ displaystyle T}$${\ displaystyle S}$${\ displaystyle T}$${\ Displaystyle T \ vdash S}$${\ Displaystyle T \ vdash \ neg S}$

První věta o neúplnosti uvádí, že jakákoli, která je konzistentní , účinná a obsahuje Robinsonovu aritmetiku („ Q “), musí být v tomto smyslu neúplná, a to výslovnou konstrukcí věty, která uvnitř není prokazatelně ani prokazatelná, ani vyvratitelná . Druhá věta o neúplnosti rozšiřuje tento výsledek tím, že ukazuje, že lze zvolit tak, aby vyjadřoval konzistenci sebe sama. ${\ displaystyle T}$${\ displaystyle S_ {T}}$${\ displaystyle T}$${\ displaystyle S_ {T}}$${\ displaystyle T}$

Jelikož to nelze vyvrátit , věta o úplnosti implikuje existenci modelu, v němž je nepravdivý. Ve skutečnosti je Π ₁ věta , tj. Uvádí, že nějaká finitistická vlastnost platí pro všechna přirozená čísla; takže pokud je nepravdivé, pak nějaké přirozené číslo je protipříkladem. Pokud by tento protipříklad existoval ve standardních přirozených číslech, jeho existence by vyvrátila uvnitř ; ale věta o neúplnosti ukázala, že to není možné, takže protipříkladem nesmí být standardní číslo, a proto jakýkoli model, v němž je nepravda, musí obsahovat nestandardní čísla . ${\ displaystyle S_ {T}}$${\ displaystyle T}$${\ displaystyle T}$${\ displaystyle S_ {T}}$${\ displaystyle S_ {T}}$${\ displaystyle S_ {T}}$${\ displaystyle T}$${\ displaystyle T}$${\ displaystyle S_ {T}}$

Ve skutečnosti je model jakékoli teorie obsahující Q získaný systematickou konstrukcí věty o existenci aritmetického modelu vždy nestandardní s neekvivalentním predikátem prokazatelnosti a neekvivalentním způsobem interpretace vlastní konstrukce, takže tato konstrukce je nerekurzivní (protože rekurzivní definice by byly jednoznačné).

Pokud je také alespoň o něco silnější než Q (např. Pokud zahrnuje indukci pro ohraničené existenciální vzorce), pak Tennenbaumova věta ukazuje, že nemá žádné rekurzivní nestandardní modely. ${\ displaystyle T}$

Vztah k větě kompaktnosti

Věta o úplnosti a věta o kompaktnosti jsou dva základní kameny logiky prvního řádu. I když ani jednu z těchto vět nelze zcela účinným způsobem dokázat , každou z nich lze účinně získat od druhé.

Věta kompaktnosti říká, že je -li formule φ logickým důsledkem (možná nekonečné) sady formulí Γ, pak je logickým důsledkem konečné podmnožiny Γ. To je bezprostřední důsledek věty o úplnosti, protože při formálním odpočtu φ lze uvést pouze konečný počet axiomů z Γ a zdravost deduktivního systému pak implikuje, že φ je logickým důsledkem této konečné množiny. Tento důkaz věty o kompaktnosti má původně na svědomí Gödel.

Naopak u mnoha deduktivních systémů je možné dokázat větu o úplnosti jako účinný důsledek věty o kompaktnosti.

Neúčinnost věty o úplnosti lze měřit v rovinách reverzní matematiky . Jsou-li uvažovány nad počitatelným jazykem, věty o úplnosti a kompaktnosti jsou navzájem ekvivalentní a ekvivalentní slabé formě volby známé jako slabé Königovo lemma , přičemž ekvivalence je prokazatelná v RCA ₀ (varianta druhého řádu Peanovy aritmetiky omezená na indukci) více než Σ ⁰ ₁ vzorce). Slabé Königovo lemma je prokazatelné v ZF, systému teorie množin Zermelo – Fraenkel bez zvoleného axiomu, a proto jsou v ZF prokazatelné věty o úplnosti a kompaktnosti pro počitatelné jazyky. Situace je však odlišná, pokud má jazyk od té doby libovolnou velkou mohutnost, ačkoli věty o úplnosti a kompaktnosti zůstávají v ZF prokazatelně navzájem ekvivalentní, jsou také prokazatelně ekvivalentní slabé formě axiomu volby známé jako ultrafiltrové lemma . Zejména žádná teorie rozšiřující ZF nemůže prokázat ani věty o úplnosti, ani o kompaktnosti nad libovolnými (možná nepočitatelnými) jazyky, aniž by také dokázala ultrafiltrové lemma na souboru stejné mohutnosti.

Úplnost v jiné logice

Věta o úplnosti je ústřední vlastností logiky prvního řádu, která neplatí pro všechny logiky. Logika druhého řádu například nemá větu úplnosti pro svou standardní sémantiku (ale má vlastnost úplnosti pro Henkinovu sémantiku ) a sada logicky platných vzorců v logice druhého řádu není rekurzivně vyčíslitelná. Totéž platí pro všechny logiky vyššího řádu. Je možné vyrábět zvukové deduktivní systémy pro logiku vyšších řádů, ale žádný takový systém nemůže být kompletní.

Lindströmova věta uvádí, že logika prvního řádu je nejsilnější (podléhá určitým omezením) logikou uspokojující kompaktnost i úplnost.

Věta o úplnosti může být prokázána pro modální logiku nebo intuitionistickou logiku s ohledem na sémantiku Kripke .

Důkazy

Gödelův původní důkaz věty pokračoval redukcí problému na speciální případ pro formule v určité syntaktické formě a následným zpracováním této formy ad hoc argumentem.

V moderních logických textech je Gödelova věta o úplnosti obvykle prokázána Henkinovým důkazem, než Gödelovým původním důkazem. Henkinův důkaz přímo vytváří termínový model pro jakoukoli konzistentní teorii prvního řádu. James Margetson (2004) vyvinul počítačový formální důkaz pomocí prověrky Isabellovy věty. Jsou známy i další důkazy.

Viz také

• Gödelovy věty o neúplnosti
• Originální důkaz Gödelovy věty o úplnosti

Další čtení

• Gödel, K (1929). „Über die Vollständigkeit des Logikkalküls“ . Disertační práce. Vídeňská univerzita. Citační deník vyžaduje |journal=( nápověda ) První důkaz věty o úplnosti.
• Gödel, K (1930). „Vollständigkeit der Axiome des logischen Funktionenkalküls“. Monatshefte für Mathematik (v němčině). 37 (1): 349–360. doi : 10,1007/BF01696781 . JFM  56,0046.04 . S2CID  123343522 . Stejný materiál jako disertační práce, s výjimkou stručnějších důkazů, stručnějších vysvětlení a vynechání zdlouhavého úvodu.

externí odkazy

• Stanfordská encyklopedie filozofie : „ Kurt Gödel “ - od Juliette Kennedyové .
• Životopis MacTutora: Kurt Gödel.
• Detlovs, Vilnis a Podnieks, Karlis, „ Úvod do matematické logiky “.