Sklon klesání - Gradient descent

Přehrávejte média

Gradient Descent ve 2D

Gradient klesání je prvního řádu iterativní optimalizační algoritmus pro nalezení lokálního minima o diferencovatelné funkce . Cílem je provést opakované kroky v opačném směru gradientu (nebo přibližného gradientu) funkce v aktuálním bodě, protože toto je směr nejstrmějšího klesání. Naopak vykročení ve směru gradientu povede k lokálnímu maximu této funkce; postup je pak znám jako gradientový výstup .

Gradientový sestup je obecně přisuzován Cauchymu , který jej poprvé navrhl v roce 1847. Hadamard nezávisle navrhl podobnou metodu v roce 1907. Jeho konvergenční vlastnosti pro problémy s nelineární optimalizací poprvé studoval Haskell Curry v roce 1944, přičemž metoda se stále více studovala. a používané v následujících desetiletích, často také nazývané nejstrmější klesání.

Popis

Ilustrace přechodu sestupu na sérii sad úrovní

Gradient klesání je založen na pozorování, že v případě, že multi-variabilní funkce je definována a diferencovatelná v okolí bodu , pak klesá nejrychleji pokud jde od ve směru záporného gradientu na . Z toho vyplývá, že pokud ${\ displaystyle F (\ mathbf {x})}$${\ displaystyle \ mathbf {a}}$${\ displaystyle F (\ mathbf {x})}$${\ displaystyle \ mathbf {a}}$${\ displaystyle F}$${\ displaystyle \ mathbf {a},-\ nabla F (\ mathbf {a})}$

${\ Displaystyle \ mathbf {a} _ {n+1} = \ mathbf {a} _ {n}-\ gamma \ nabla F (\ mathbf {a} _ {n})}$

tedy na dostatečně malou . Jinými slovy, výraz je odečten, protože se chceme pohybovat proti přechodu směrem k místnímu minimu. S ohledem na toto pozorování člověk začíná odhadem lokálního minima a považuje sekvenci za takovou ${\ displaystyle \ gamma \ in \ mathbb {R} _ {+}}$${\ displaystyle F (\ mathbf {a_ {n}}) \ geq F (\ mathbf {a_ {n+1}})}$${\ displaystyle \ gamma \ nabla F (\ mathbf {a})}$${\ displaystyle \ mathbf {a}}$${\ displaystyle \ mathbf {x} _ {0}}$${\ displaystyle F}$${\ Displaystyle \ mathbf {x} _ {0}, \ mathbf {x} _ {1}, \ mathbf {x} _ {2}, \ ldots}$

${\ Displaystyle \ mathbf {x} _ {n+1} = \ mathbf {x} _ {n}-\ gamma _ {n} \ nabla F (\ mathbf {x} _ {n}), \ n \ geq 0.}$

Máme monotónní posloupnost

${\ Displaystyle F (\ mathbf {x} _ {0}) \ geq F (\ mathbf {x} _ {1}) \ geq F (\ mathbf {x} _ {2}) \ geq \ cdots,}$

doufejme, že posloupnost konverguje k požadovanému místnímu minimu. Všimněte si toho, že hodnota velikosti kroku se může měnit při každé iteraci. S určitými předpoklady funkce (například konvexní a Lipschitz ) a konkrétními možnostmi (např. Zvolenými buď pomocí řádkového vyhledávání, které splňuje podmínky Wolfe , nebo metodou Barzilai – Borwein ukázanou níže), ${\ displaystyle (\ mathbf {x} _ {n})}$ ${\ displaystyle \ gamma}$${\ displaystyle F}$${\ displaystyle F}$ ${\ displaystyle \ nabla F}$ ${\ displaystyle \ gamma}$

${\ Displaystyle \ gamma _ {n} = {\ frac {\ left | \ left (\ mathbf {x} _ {n}-\ mathbf {x} _ {n-1} \ right)^{T} \ left [\ nabla F (\ mathbf {x} _ {n})-\ nabla F (\ mathbf {x} _ {n-1}) \ right] \ right |} {\ left \ | \ nabla F (\ mathbf {x} _ {n})-\ nabla F (\ mathbf {x} _ {n-1}) \ right \ |^{2}}}}$

lze zaručit konvergenci na místní minimum. Je-li funkce je konvexní , všechny lokální minima jsou také globální minima, takže v tomto případě gradientu sestupu může konvergovat ke globálnímu řešení. ${\ displaystyle F}$

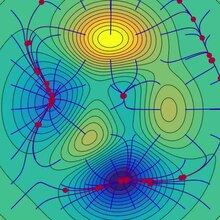
Tento proces je znázorněn na sousedním obrázku. Zde se předpokládá, že je definován v rovině, a že jeho graf má tvar misky . Modré křivky jsou vrstevnice , tj. Oblasti, ve kterých je hodnota konstantní. Červená šipka pocházející z bodu ukazuje směr negativního přechodu v tomto bodě. Všimněte si, že (negativní) gradient v bodě je ortogonální k vrstevnici procházející tímto bodem. Vidíme, že gradientový sestup nás vede ke dnu mísy, tedy do bodu, kde je hodnota funkce minimální. ${\ displaystyle F}$${\ displaystyle F}$${\ displaystyle F}$

Analogie pro pochopení gradientového sestupu

Mlha v horách

Základní intuici za klesáním lze ilustrovat na hypotetickém scénáři. Člověk uvízl v horách a snaží se dostat dolů (tj. Snaží se najít globální minimum). Je hustá mlha, takže viditelnost je extrémně nízká. Proto cesta dolů z hory není vidět, a tak musí k nalezení minima použít místní informace. Mohou použít metodu gradientového klesání, která zahrnuje pohled na strmost kopce v jejich aktuální poloze, poté postup ve směru s nejstrmějším klesáním (tj. Z kopce). Pokud se pokoušeli najít vrchol hory (tj. Maximum), postupovali by ve směru nejstrmějšího stoupání (tj. Do kopce). Pomocí této metody by nakonec našli cestu dolů z hory nebo by se mohli zaseknout v nějaké díře (tj. Místním minimu nebo sedlovém bodě ), jako horské jezero. Předpokládejme však také, že strmost kopce není při jednoduchém pozorování hned zřejmá, ale spíše vyžaduje promyšlený nástroj k měření, který dotyčný v danou chvíli náhodou má. Měření strmosti kopce nástrojem trvá docela dlouho, a proto by měli minimalizovat používání nástroje, pokud se chtěli dostat z hory před západem slunce. Obtížností pak je zvolit frekvenci, s jakou by měli měřit strmost kopce, aby nevyjížděli ze stopy.

V této analogii osoba představuje algoritmus a cesta vedená po horách představuje posloupnost nastavení parametrů, které algoritmus prozkoumá. Strmost kopce představuje sklon chybové plochy v daném bodě. Přístroj používaný k měření strmosti je diferenciace (sklon chybové plochy lze vypočítat derivací funkce čtvercové chyby v daném bodě). Směr, kterým se rozhodnou cestovat, je v souladu s gradientem chybové plochy v daném bodě. Doba, kterou stráví před provedením dalšího měření, je velikost kroku.

Příklady

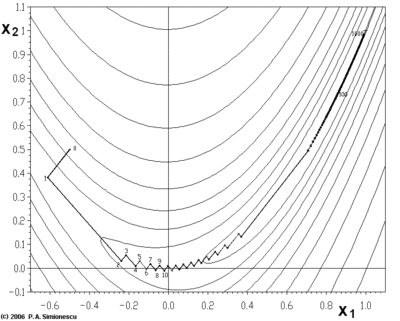
Gradientový sestup má problémy s patologickými funkcemi, jako je zde zobrazená Rosenbrockova funkce .

${\ Displaystyle f (x_ {1}, x_ {2}) = (1-x_ {1})^{2} +100 (x_ {2} -x_ {1}^{2})^{2} }$

Funkce Rosenbrock má úzké zakřivené údolí, které obsahuje minimum. Dno údolí je velmi ploché. Kvůli zakřivenému plochému údolí optimalizace pomalu kličkuje s malými velikostmi kroků směrem k minimu. Whiplash Gradient Descent řeší tento problém zvlášť.

Klikatá povaha metody je také evidentní níže, kde je aplikována metoda sestupného gradientu

${\ Displaystyle F (x, y) = \ sin \ left ({\ frac {1} {2}} x^{2}-{\ frac {1} {4}} y^{2} +3 \ right ) \ cos \ left (2x+1-e^{y} \ right).}$

Volba velikosti kroku a směru klesání

Protože použití příliš malé velikosti kroku by zpomalilo konvergenci a příliš velké by vedlo k divergenci, je nalezení dobrého nastavení důležitým praktickým problémem. Philip Wolfe také obhajoval používání „chytrých voleb směru [sestupu]“ v praxi. Zatímco použití směru, který se odchyluje od nejstrmějšího směru sestupu, se může zdát neintuitivní, myšlenka je, že menší sklon může být kompenzován tím, že bude udržován na mnohem delší vzdálenosti. ${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$

Abychom o tom mohli uvažovat matematicky, použijme velikost směru a kroku a zvažme obecnější aktualizaci: ${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$

${\ Displaystyle \ mathbf {a} _ {n+1} = \ mathbf {a} _ {n}-\ gamma _ {n} \, \ mathbf {p} _ {n}}$.

Nalezení dobrého nastavení a vyžaduje trochu přemýšlení. Nejprve bychom chtěli, aby směr aktualizace směřoval z kopce. Matematicky, nechat označovat úhel mezi, a to vyžaduje, abychom řekli více, potřebujeme více informací o objektivní funkci, kterou optimalizujeme. Za poměrně slabého předpokladu, který je průběžně diferencovatelný, můžeme dokázat, že: ${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$${\ displaystyle \ theta _ {n}}$${\ displaystyle \ nabla F (\ mathbf {a_ {n}})}$${\ displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ cos \ theta _ {n}> 0.}$${\ displaystyle F}$

${\ Displaystyle F (\ mathbf {a} _ {n+1}) \ leq F (\ mathbf {a} _ {n})-\ gamma _ {n} \ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2} \ | \ mathbf {p} _ {n} \ | _ {2} \ left [\ cos \ theta _ {n}-\ max _ {t \ in [0,1 ]} {\ frac {\ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n})-\ nabla F (\ mathbf {a} _ {n}) \ | _ {2}} {\ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}}} \ right]}$

( 1 )

Tato nerovnost znamená, že částka, o kterou si můžeme být jisti, že je funkce snížena, závisí na kompromisu mezi těmito dvěma termíny v hranatých závorkách. První člen v hranatých závorkách měří úhel mezi směrem sestupu a záporným přechodem. Druhý termín měří, jak rychle se přechod mění ve směru sestupu. ${\ displaystyle F}$

V zásadě by nerovnost ( 1 ) mohla být optimalizována a zvolit optimální velikost a směr kroku. Problém je v tom, že vyhodnocení druhého členu v hranatých závorkách vyžaduje vyhodnocení a další hodnocení gradientů je obecně nákladné a nežádoucí. Některé způsoby, jak tento problém vyřešit, jsou: ${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$${\ Displaystyle \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n})}$

• Zřekněte se výhod chytrého směru sestupu nastavením a pomocí řádkového vyhledávání najděte vhodnou velikost kroku , například takovou, která splňuje podmínky Wolfe .${\ displaystyle \ mathbf {p} _ {n} = \ nabla F (\ mathbf {a_ {n}})}$${\ displaystyle \ gamma _ {n}}$
• Za předpokladu, že je to dvakrát diferencovatelné, použijte jeho pytlovinu k odhadu Pak vyberte a optimalizací nerovnosti ( 1 ).${\ displaystyle F}$${\ displaystyle \ nabla ^{2} F}$${\ Displaystyle \ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n})-\ nabla F (\ mathbf {a} _ {n} ) \ | _ {2} \ cca \ | t \ gamma _ {n} \ nabla ^{2} F (\ mathbf {a} _ {n}) \ mathbf {p} _ {n} \ |.}$${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$
• Za předpokladu, že je to Lipschitz , použijte jeho Lipschitzovu konstantu k ohraničení Pak zvolte a optimalizací nerovnosti ( 1 ).${\ displaystyle \ nabla F}$${\ displaystyle L}$${\ Displaystyle \ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n})-\ nabla F (\ mathbf {a} _ {n} ) \ | _ {2} \ leq Lt \ gamma _ {n} \ | \ mathbf {p} _ {n} \ |.}$${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$
• Vytvořte si vlastní model pro . Poté zvolte a optimalizací nerovnosti ( 1 ).${\ Displaystyle \ max _ {t \ in [0,1]} {\ frac {\ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ { n})-\ nabla F (\ mathbf {a} _ {n}) \ | _ {2}} {\ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}}} }$${\ displaystyle F}$${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$
• Za silnějších předpokladů funkce, jako je konvexita , mohou být možné pokročilejší techniky .${\ displaystyle F}$

Obvykle při dodržení jednoho z výše uvedených receptů lze zaručit konvergenci k místnímu minimu. Je-li funkce je konvexní , všechny lokální minima jsou také globální minima, takže v tomto případě gradientu sestupu může konvergovat ke globálnímu řešení. ${\ displaystyle F}$

Řešení lineárního systému

Algoritmus nejstrmějšího klesání aplikovaný na Wienerův filtr

Gradient descent lze použít k řešení soustavy lineárních rovnic

${\ Displaystyle A \ mathbf {x} -\ mathbf {b} = 0}$

přeformulován jako problém kvadratické minimalizace. Pokud je matice systému skutečná symetrická a pozitivně definovaná , je objektivní funkce definována jako kvadratická funkce s minimalizací ${\ displaystyle A}$

${\ Displaystyle F (\ mathbf {x}) = \ mathbf {x} ^{T} A \ mathbf {x} -2 \ mathbf {x} ^{T} \ mathbf {b},}$

aby

${\ Displaystyle \ nabla F (\ mathbf {x}) = 2 (A \ mathbf {x} -\ mathbf {b}).}$

Pro obecný skutečné matice , lineární metodou nejmenších čtverců definovat ${\ displaystyle A}$

${\ Displaystyle F (\ mathbf {x}) = \ left \ | A \ mathbf {x} -\ mathbf {b} \ right \ |^{2}.}$

V tradičních lineární metodou nejmenších čtverců pro skutečné a na euklidovské normy se používá, a v tomto případě ${\ displaystyle A}$${\ displaystyle \ mathbf {b}}$

${\ Displaystyle \ nabla F (\ mathbf {x}) = 2A^{T} (A \ mathbf {x} -\ mathbf {b}).}$

Linka vyhledávání Minimalizace, zjištění místně optimální velikost kroku na každé iteraci, může být provedena analyticky pro kvadratické funkce a explicitních vzorců pro místně optimální nejsou známy. ${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$

Například pro skutečnou symetrickou a pozitivně definovanou matici může jednoduchý algoritmus vypadat následovně, ${\ displaystyle A}$

${\ Displaystyle {\ begin {aligned} & {\ text {opakujte ve smyčce:}} \\ & \ qquad \ mathbf {r}: = \ mathbf {b} -\ mathbf {Ax} \\ & \ qquad \ gamma: = {\ mathbf {r} ^{\ mathsf {T}} \ mathbf {r}}/{\ mathbf {r} ^{\ mathsf {T}} \ mathbf {Ar}} \\ & \ qquad \ mathbf {x}: = \ mathbf {x} +\ gamma \ mathbf {r} \\ & \ qquad {\ hbox {if}} \ mathbf {r} ^{\ mathsf {T}} \ mathbf {r} { \ text {je dostatečně malý, poté ukončete smyčku}} \\ & {\ text {end opakování smyčky}} \\ & {\ text {return}} \ mathbf {x} {\ text {jako výsledek}} \ end {zarovnaný}}}$

Abychom se vyhnuli násobení dvakrát za iteraci, poznamenáváme, že to znamená , což dává tradiční algoritmus, ${\ displaystyle A}$${\ Displaystyle \ mathbf {x}: = \ mathbf {x} +\ gamma \ mathbf {r}}$${\ Displaystyle \ mathbf {r}: = \ mathbf {r} -\ gamma \ mathbf {Ar}}$

${\ Displaystyle {\ begin {aligned} & \ mathbf {r}: = \ mathbf {b} -\ mathbf {Ax} \\ & {\ text {opakujte ve smyčce:}} \\ & \ qquad \ gamma: = {\ mathbf {r} ^{\ mathsf {T}} \ mathbf {r}}/{\ mathbf {r} ^{\ mathsf {T}} \ mathbf {Ar}} \\ & \ qquad \ mathbf { x}: = \ mathbf {x} +\ gamma \ mathbf {r} \\ & \ qquad {\ hbox {if}} \ mathbf {r} ^{\ mathsf {T}} \ mathbf {r} {\ text {je dostatečně malý, poté ukončete smyčku}} \\ & \ qquad \ mathbf {r}: = \ mathbf {r} -\ gamma \ mathbf {Ar} \\ & {\ text {end repeat loop}} \\ & {\ text {return}} \ mathbf {x} {\ text {jako výsledek}} \ end {aligned}}}$

Metoda se zřídka používá k řešení lineárních rovnic, přičemž metoda konjugovaného gradientu je jednou z nejpopulárnějších alternativ. Počet poklesu gradientu iterací je obecně úměrná spektrální číslo stavu systémové matrice (poměr maximální na minimální vlastní hodnoty o ) , přičemž konvergence metody sdružených gradientů je obvykle určena odmocnině počtu stavu, tedy , je mnohem rychlejší. Obě metody mohou těžit z předběžného kondicionování , kde gradientový sestup může vyžadovat méně předpokladů na kondicionéru. ${\ displaystyle \ kappa (A)}$${\ displaystyle A}$${\ displaystyle A^{T} A}$

Řešení nelineárního systému

Gradient descent lze také použít k řešení soustavy nelineárních rovnic . Níže je uveden příklad, který ukazuje, jak pomocí sestupu přechodu vyřešit tři neznámé proměnné x ₁ , x ₂ a x ₃ . Tento příklad ukazuje jednu iteraci gradientového sestupu.

Uvažujme nelineární soustavu rovnic

${\ Displaystyle {\ begin {cases} 3x_ {1}-\ cos (x_ {2} x_ {3})-{\ tfrac {3} {2}} = 0 \\ 4x_ {1}^{2}- 625x_ {2}^{2}+2x_ {2} -1 = 0 \\\ exp (-x_ {1} x_ {2})+20x_ {3}+{\ tfrac {10 \ pi -3} {3 }} = 0 \ end {případů}}}$

Pojďme si představit přidruženou funkci

${\ Displaystyle G (\ mathbf {x}) = {\ begin {bmatrix} 3x_ {1}-\ cos (x_ {2} x_ {3})-{\ tfrac {3} {2}} \\ 4x_ { 1}^{2} -625x_ {2}^{2}+2x_ {2} -1 \\\ exp (-x_ {1} x_ {2})+20x_ {3}+{\ tfrac {10 \ pi -3} {3}} \\\ end {bmatrix}},}$

kde

${\ Displaystyle \ mathbf {x} = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\ x_ {3} \\\ end {bmatrix}}.}$

Nyní lze definovat objektivní funkci

${\ Displaystyle F (\ mathbf {x}) = {\ frac {1} {2}} G^{\ mathrm {T}} (\ mathbf {x}) G (\ mathbf {x}) = {\ frac {1} {2}} \ left [\ left (3x_ {1}-\ cos (x_ {2} x_ {3})-{\ frac {3} {2}} \ right)^{2}+\ vlevo (4x_ {1}^{2} -625x_ {2}^{2}+2x_ {2} -1 \ vpravo)^{2}+\ vlevo (\ exp (-x_ {1} x_ {2}) +20x_ {3}+{\ frac {10 \ pi -3} {3}} \ right)^{2} \ right],}$

které se pokusíme minimalizovat. Jako počáteční odhad použijme

${\ Displaystyle \ mathbf {x} ^{(0)} = \ mathbf {0} = {\ begin {bmatrix} 0 \\ 0 \\ 0 \\\ end {bmatrix}}.}$

Víme, že

${\ Displaystyle \ mathbf {x} ^{(1)} = \ mathbf {0} -\ gamma _ {0} \ nabla F (\ mathbf {0}) = \ mathbf {0} -\ gamma _ {0} J_ {G} (\ mathbf {0})^{\ mathrm {T}} G ​​(\ mathbf {0}),}$

kde je jakobijská matice dána vztahem ${\ displaystyle J_ {G}}$

${\ Displaystyle J_ {G} (\ mathbf {x}) = {\ begin {bmatrix} 3 & \ sin (x_ {2} x_ {3}) x_ {3} & \ sin (x_ {2} x_ {3} ) x_ {2} \\ 8x_ {1} &-1250x_ {2}+2 & 0 \\-x_ {2} \ exp {(-x_ {1} x_ {2})} &-x_ {1} \ exp ( -x_ {1} x_ {2}) & 20 \\\ end {bmatrix}}.}$

Vypočítáme:

${\ Displaystyle J_ {G} (\ mathbf {0}) = {\ begin {bmatrix} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 20 \ end {bmatrix}}, \ qquad G (\ mathbf {0}) = {\ begin { bmatrix} -2,5 \\-1 \\ 10,472 \ end {bmatrix}}.}$

Tím pádem

${\ Displaystyle \ mathbf {x} ^{(1)} = \ mathbf {0}-\ gamma _ {0} {\ begin {bmatrix} -7,5 \\-2 \\ 209,44 \ end {bmatrix}},}$

a

${\ Displaystyle F (\ mathbf {0}) = 0,5 \ left ((--2,5)^{2}+(-1)^{2}+(10,472)^{2} \ right) = 58,456.}$

Na tento příklad byla použita animace zobrazující prvních 83 iterací klesání. Plochy jsou povrchy podle aktuálního odhadu a šipky ukazují směr sestupu. Vzhledem k malé a konstantní velikosti kroku je konvergence pomalá.${\ Displaystyle F (\ mathbf {x} ^{(n)})}}$${\ displaystyle \ mathbf {x} ^{(n)}}$

Nyní se musí najít vhodný takový, aby ${\ displaystyle \ gamma _ {0}}$

${\ Displaystyle F \ left (\ mathbf {x} ^{(1)} \ right) \ leq F \ left (\ mathbf {x} ^{(0)} \ right) = F (\ mathbf {0}) .}$

To lze provést pomocí libovolného z řady algoritmů pro řádkové vyhledávání . Dalo by se také jednoduše hádat, co dává ${\ displaystyle \ gamma _ {0} = 0,001,}$

${\ Displaystyle \ mathbf {x} ^{(1)} = {\ begin {bmatrix} 0,0075 \\ 0,002 \\-0,20944 \\\ end {bmatrix}}.}$

Vyhodnocení objektivní funkce na této hodnotě, výnosy

${\ Displaystyle F \ left (\ mathbf {x}^{(1)} \ right) = 0,5 \ left ((-2,48)^{2}+(-1,00)^{2}+(6,28)^{2 } \ right) = 23.306.}$

Snížení z na hodnotu následujícího kroku ${\ Displaystyle F (\ mathbf {0}) = 58,456}$

${\ Displaystyle F \ left (\ mathbf {x} ^{(1)} \ right) = 23.306}$

je značný pokles objektivní funkce. Další kroky by jeho hodnotu dále snižovaly, dokud by nebylo nalezeno přibližné řešení systému.

Komentáře

Gradient descent funguje v prostorech libovolného počtu dimenzí, dokonce i v nekonečně dimenzionálních. V druhém případě je vyhledávací prostor obvykle funkčním prostorem a vypočítá se Fréchetova derivace funkčního prvku, který má být minimalizován, aby se určil směr sestupu.

Že gradientový sestup funguje v libovolném počtu dimenzí (alespoň konečný počet), lze považovat za důsledek Cauchy-Schwarzovy nerovnosti . Tento článek dokazuje, že velikost vnitřního (tečkového) součinu dvou vektorů jakékoli dimenze je maximalizována, když jsou kolineární. V případě gradientového sestupu by to bylo tehdy, když je vektor nezávislých variabilních úprav úměrný gradientovému vektoru parciálních derivací.

Pokud je zakřivení v různých směrech pro danou funkci velmi odlišné, může gradientový sestup počítat mnoho iterací pro výpočet lokálního minima s požadovanou přesností . U takových funkcí předkondicionování , které mění geometrii prostoru tak, aby tvarovalo sady úrovní funkcí, jako jsou soustředné kruhy , léčí pomalou konvergenci. Konstrukce a použití předběžné úpravy však mohou být výpočetně nákladné.

Klesání gradientu lze kombinovat s hledáním řádků , při každé iteraci se najde lokálně optimální velikost kroku. Provádění řádkového vyhledávání může být časově náročné. Naopak použití fixní malé může vést ke špatné konvergenci. ${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$

Lepšími alternativami mohou být metody založené na Newtonově metodě a inverzi Hessianů pomocí technik konjugovaného gradientu . Obecně se takové metody sbližují v menším počtu iterací, ale náklady na každou iteraci jsou vyšší. Příkladem je metoda BFGS, která spočívá ve výpočtu na každém kroku matice, pomocí které se násobí vektor přechodu, aby se dostal do „lepšího“ směru, v kombinaci se sofistikovanějším algoritmem pro vyhledávání řádků , abychom našli „nejlepší“ hodnotu For extrémně velké problémy, kde dominují problémy s pamětí počítače, měla by být použita metoda omezené paměti, jako je L-BFGS, místo BFGS nebo nejstrmější klesání. ${\ displaystyle \ gamma.}$

Na gradientový sestup lze pohlížet jako na použití Eulerovy metody pro řešení běžných diferenciálních rovnic na gradientový tok . Na druhé straně může být tato rovnice odvozena jako optimální regulátor pro řídicí systém s uvedením ve formě zpětné vazby . ${\ Displaystyle x '(t) =-\ nabla f (x (t))}$${\ Displaystyle x '(t) = u (t)}$${\ displaystyle u (t)}$${\ Displaystyle u (t) =-\ nabla f (x (t))}$

Modifikace

Gradientový sestup se může sbíhat na místní minimum a zpomalovat v sousedství sedlového bodu . I pro neomezenou kvadratickou minimalizaci gradientový sestup vyvíjí cik-cak vzor následných iterací, jak iterace postupují, což má za následek pomalou konvergenci. K řešení těchto nedostatků bylo navrženo několik modifikací klesání.

Metody rychlého přechodu

Yurii Nesterov navrhl jednoduchou modifikaci, která umožňuje rychlejší konvergenci konvexních problémů a od té doby se dále generalizuje. Pro neomezené hladké problémy se tato metoda nazývá metoda rychlého přechodu (FGM) nebo metoda zrychleného přechodu (AGM). Konkrétně, pokud je diferencovatelná funkce konvexní a je Lipschitzova a nepředpokládá se, že je silně konvexní , pak bude chyba v objektivní hodnotě generované v každém kroku metodou gradientového sestupu ohraničena . Pomocí Nesterovovy akcelerační techniky se chyba snižuje při . Je známo, že míra pro snížení nákladové funkce je optimální pro optimalizační metody prvního řádu. Existuje však příležitost vylepšit algoritmus snížením konstantního faktoru. Optimalizována metoda gradientu (OGM) snižuje, že konstanta o faktor dva a je metoda optimální prvního řádu pro problémy ve velkém měřítku. ${\ displaystyle F}$${\ displaystyle \ nabla F}$${\ displaystyle F}$${\ displaystyle k}$ ${\ textstyle {\ mathcal {O}} \ left ({\ tfrac {1} {k}} \ right)}$${\ textstyle {\ mathcal {O}} \ left ({\ tfrac {1} {k^{2}}} \ right)}$${\ displaystyle {\ mathcal {O}} \ left ({k^{-2}} \ right)}$

U omezených nebo nehladkých problémů se Nesterovova FGM nazývá metoda rychlého proximálního gradientu (FPGM), zrychlení metody proximálního gradientu .

Metoda hybnosti nebo těžkého míče

Snaží prolomit klikatá vzor poklesu gradientu se hybnost nebo těžký způsob koule používá hybnost termín v analogii k těžkým míč posuvné na povrchu hodnot funkce je minimalizována, nebo pohybu hmoty v newtonovské dynamiky prostřednictvím Viskozní médium v ​​konzervativním silovém poli. Gradient descent with hybnost si pamatuje aktualizaci řešení při každé iteraci a určuje další aktualizaci jako lineární kombinaci přechodu a předchozí aktualizace. Pro neomezenou kvadratickou minimalizaci je hranice teoretické míry konvergence metody těžké koule asymptoticky stejná jako pro metodu optimálního gradientu konjugátu .

Tato technika se používá v Stochastic gradient descent#Momentum a jako rozšíření algoritmů zpětné propagace používaných k trénování umělých neuronových sítí .

Rozšíření

Klesání gradientu lze prodloužit tak, aby zvládalo omezení zahrnutím projekce na sadu omezení. Tato metoda je realizovatelná pouze tehdy, když je projekce efektivně vyčíslitelná na počítači. Za vhodných předpokladů tato metoda konverguje. Tato metoda je specifickým případem dopředně-zpětného algoritmu pro monotónní inkluze (který zahrnuje konvexní programování a variační nerovnosti ).

Viz také

Reference

Další čtení

• Boyd, Stephen ; Vandenberghe, Lieven (2004). „Neomezená minimalizace“ (PDF) . Konvexní optimalizace . New York: Cambridge University Press. s. 457–520. ISBN 0-521-83378-7.
• Chong, Edwin KP; Żak, Stanislaw H. (2013). „Přechodové metody“ . Úvod do optimalizace (čtvrté vydání). Hoboken: Wiley. s. 131–160. ISBN 978-1-118-27901-4.
• Himmelblau, David M. (1972). „Neomezené minimalizační postupy využívající deriváty“. Aplikované nelineární programování . New York: McGraw-Hill. s. 63–132. ISBN 0-07-028921-2.

externí odkazy

• Použití gradientového klesání v C ++, Boost, Ublas pro lineární regresi
• Série videí Khan Academy pojednává o stoupání
• Online kniha s výukou gradientu v kontextu hluboké neuronové sítě
• „Gradient Descent, How Neural Networks Learn“ . 3Modrá1Hnědá . 16. října 2017 - prostřednictvím YouTube .

arxiv.org/2108.1283