Greedy algoritmus - Greedy algorithm

Chamtivé algoritmy určují minimální počet mincí, které lze při změně dát. Toto jsou kroky, které by většina lidí podnikla k napodobení chamtivého algoritmu, který by představoval 36 centů a používal pouze mince s hodnotami {1, 5, 10, 20}. Mince nejvyšší hodnoty, menší než zbývající dlužná změna, je místní optimum. ( Problém změny tvorby obecně vyžaduje dynamické programování, aby bylo nalezeno optimální řešení; většina měnových systémů, včetně eura a amerického dolaru, je však zvláštním případem, kdy chamtivá strategie najde optimální řešení.)

Chamtivý algoritmus je nějaký algoritmus , který navazuje na řešení problémů heuristické tvorby místně optimální volbu v každé fázi. V mnoha problémech chamtivá strategie nepřináší optimální řešení, ale chamtivý heurista může poskytnout lokálně optimální řešení, která se v rozumném čase přiblíží globálně optimálnímu řešení.

Chamtivá strategie pro problém obchodního cestujícího (která má vysokou výpočetní náročnost) je například následující heuristika: „V každém kroku cesty navštivte nejbližší nenavštívené město.“ Tato heuristika nemá v úmyslu najít nejlepší řešení, ale končí v rozumném počtu kroků; nalezení optimálního řešení tak složitého problému obvykle vyžaduje nepřiměřeně mnoho kroků. V matematické optimalizaci chamtivé algoritmy optimálně řeší kombinatorické úlohy s vlastnostmi matroidů a poskytují aproximace konstantních faktorů optimalizačním problémům se submodulární strukturou.

Specifika

Chamtivé algoritmy mají obecně pět složek:

1. Sada kandidátů, ze které je vytvořeno řešení
2. Funkce výběru, která vybere nejlepšího kandidáta, který má být přidán do řešení
3. Funkce proveditelnosti, která se používá k určení, zda lze kandidáta použít k přispění k řešení
4. Objektivní funkce, která přiřazuje hodnotu řešení nebo částečnému řešení, a
5. Funkce řešení, která ukáže, kdy jsme objevili kompletní řešení

Chamtivé algoritmy vytvářejí dobrá řešení pro některé matematické problémy , pro jiné nikoli. Většina problémů, pro které fungují, bude mít dvě vlastnosti:

Chamtivý výběr nemovitosti

Můžeme učinit jakoukoli volbu, která se nám v tuto chvíli zdá nejlepší, a poté vyřešit dílčí problémy, které nastanou později. Volba chamtivým algoritmem může záviset na dosud provedených volbách, ale ne na budoucích rozhodnutích nebo na všech řešeních podproblému. Iterativně dělá jednu chamtivou volbu za druhou a redukuje každý daný problém na menší. Jinými slovy, chamtivý algoritmus nikdy nepřehodnotí své volby. To je hlavní rozdíl od dynamického programování , které je vyčerpávající a zaručeně najde řešení. Po každé fázi se dynamické programování rozhoduje na základě všech rozhodnutí učiněných v předchozí fázi a může přehodnotit algoritmickou cestu předchozího stupně k řešení.

Optimální spodní konstrukce

„Problém vykazuje optimální substrukturu, pokud optimální řešení problému obsahuje optimální řešení dílčích problémů.“

Případy selhání

Příklady toho, jak chamtivý algoritmus nemusí dosáhnout optimálního řešení.

Počínaje od A, chamtivý algoritmus, který se pokusí najít maximum sledováním největšího sklonu, najde místní maximum na „m“, přičemž zapomíná na globální maximum na „M“.

Aby dosáhl největšího součtu, v každém kroku chamtivý algoritmus zvolí to, co se jeví jako optimální okamžitá volba, takže v druhém kroku zvolí 12 místo 3 a nedosáhne nejlepšího řešení, které obsahuje 99.

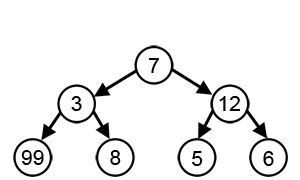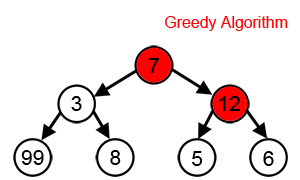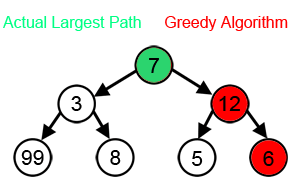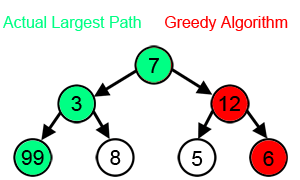
Chamtivé algoritmy nedokážou vytvořit optimální řešení pro mnoho dalších problémů a mohou dokonce vytvořit jedinečné nejhorší možné řešení. Jedním z příkladů je výše zmíněný problém obchodního cestujícího : u každého počtu měst existuje přiřazení vzdáleností mezi městy, pro která heuristika nejbližšího souseda vytváří jedinečnou nejhorší možnou cestu. Další možné příklady viz efekt horizontu .

Typy

Chamtivé algoritmy lze charakterizovat jako „krátkozraké“ a také jako „neobnovitelné“. Jsou ideální pouze pro problémy, které mají „optimální spodní konstrukci“. Navzdory tomu jsou u mnoha jednoduchých problémů chamtiví nejvhodnější algoritmy. Je však důležité si uvědomit, že chamtivý algoritmus lze použít jako výběrový algoritmus k upřednostnění možností v rámci vyhledávacího algoritmu nebo algoritmu větve a vazby. Chamtivý algoritmus má několik variant:

• Čistě chamtivé algoritmy
• Ortogonální chamtivé algoritmy
• Uvolněné chamtivé algoritmy

Teorie

Greedy algoritmy mají dlouhou historii studia v kombinatorické optimalizaci a teoretické informatice . O chamtivé heuristice je známo, že produkuje suboptimální výsledky pro mnoho problémů, a proto přirozené otázky jsou:

• Pro jaké problémy fungují chamtivé algoritmy optimálně?
• U jakých problémů zaručují chamtivé algoritmy přibližně optimální řešení?
• Pro které problémy jsou chamtivý algoritmus zaručena není produkovat optimální řešení?

Existuje velké množství literatury, která na tyto otázky odpovídá jak pro obecné třídy problémů, jako jsou matroidy , tak i pro specifické problémy, jako je sada krytí .

Matroidi

Matroid je matematická struktura, která zobecňuje pojem lineární nezávislosti od vektorových prostorů do libovolných sestav. Pokud má problém s optimalizací strukturu matroidu, pak jej příslušný chamtivý algoritmus optimálně vyřeší.

Submodulární funkce

Funkce definovaná v podmnožinách množiny se nazývá submodulární, pokud ji máme pro každého . ${\ displaystyle f}$${\ displaystyle \ Omega}$${\ Displaystyle S, T \ subseteq \ Omega}$${\ Displaystyle f (S)+f (T) \ geq f (S \ cup T)+f (S \ cap T)}$

Předpokládejme, že člověk chce najít sadu, která maximalizuje . Chamtivý algoritmus, který vytváří sadu postupným přidáváním prvku, který se v každém kroku zvyšuje nejvíce, produkuje jako výstup alespoň sadu . To znamená, že chamtivý funguje v rámci konstantního faktoru tak dobrého, jako je optimální řešení. ${\ displaystyle S}$${\ displaystyle f}$${\ displaystyle S}$${\ displaystyle f}$${\ Displaystyle (1-1/e) \ max _ {X \ subseteq \ Omega} f (X)}$${\ Displaystyle (1-1/e) \ cca 0,63}$

Podobné záruky jsou prokazatelné, když jsou na výstup uvalena další omezení, například omezení mohutnosti, ačkoli často jsou vyžadovány mírné odchylky chamtivého algoritmu. Podívejte se na přehled.

Další problémy se zárukami

Mezi další problémy, pro které chamtivý algoritmus poskytuje silnou záruku, ale ne optimální řešení, patří

• Nastavit kryt
• Problém Steinerova stromu
• Vyrovnávání zátěže
• Nezávislá sada

Mnoho z těchto problémů má odpovídající spodní hranice; tj. chamtivý algoritmus nefunguje v nejhorším případě lépe než záruka.

Aplikace

Chamtivé algoritmy obvykle (ale ne vždy) nedokážou najít globálně optimální řešení, protože obvykle nepracují vyčerpávajícím způsobem na všech datech. Mohou se zavázat k určitým rozhodnutím příliš brzy, což jim brání později najít nejlepší celkové řešení. Například všechny známé chamtivé zbarvovací algoritmy pro problém zbarvení grafu a všechny ostatní problémy s úplným NP nenacházejí konzistentně optimální řešení. Přesto jsou užitečné, protože se rychle rozmyslí a často optimálně přiblíží.

Pokud lze prokázat chamtivý algoritmus, který poskytne globální optimum pro danou třídu problémů, obvykle se stane metodou volby, protože je rychlejší než jiné optimalizační metody, jako je dynamické programování . Příklady takových chamtivých algoritmů jsou Kruskalův algoritmus a Primův algoritmus pro nalezení stromů minimálního překlenutí a algoritmus pro nalezení optimálních Huffmanových stromů .

Greedy algoritmy se objevují také ve směrování sítě . Pomocí chamtivého směrování je zpráva předána sousednímu uzlu, který je „nejblíže“ cíli. Pojem polohy uzlu (a tedy „blízkost“) může být určen jeho fyzickým umístěním, jako v geografickém směrování používaném sítěmi ad hoc . Umístění může být také zcela umělou konstrukcí, jako v malém světě směrování a distribuované hashovací tabulce .

Příklady

• Problém výběru aktivit je charakteristický pro tuto třídu problémů, kde je cílem vybrat maximální počet aktivit, které se navzájem neslučují.
• V počítačové hře Macintosh Crystal Quest je cílem sbírat krystaly, podobným způsobem jako problém obchodního cestujícího . Hra má demo režim, kde hra pomocí chamtivého algoritmu přejde ke každému krystalu. Umělá inteligence neodpovídá za překážky, takže demo režim často skončí rychle.
• Odpovídající výkon je příkladem chamtivý algoritmus aplikovaný na signálu sbližování.
• Chamtivý algoritmus najde optimální řešení Malfattiho problému nalezení tří disjunktních kruhů v daném trojúhelníku, které maximalizují celkovou plochu kruhů; předpokládá se, že stejný chamtivý algoritmus je optimální pro libovolný počet kruhů.
• K sestavení Huffmanova stromu během Huffmanova kódování se používá chamtivý algoritmus, kde najde optimální řešení.
• Při učení rozhodovacího stromu se běžně používají chamtivé algoritmy, ale není zaručeno, že najdou optimální řešení.
  • Jeden populární takový algoritmus je ID3 algoritmus pro rozhodovací stromovou konstrukci.
• Algoritmus Dijkstra a související vyhledávací algoritmus A* jsou prokazatelně optimální chamtivé algoritmy pro vyhledávání grafů a hledání nejkratších cest .
  • Hledání* je podmíněně optimální a vyžaduje „ přípustnou heuristiku “, která nebude nadhodnocovat náklady na cestu.
• Kruskalův algoritmus a Primův algoritmus jsou chamtivé algoritmy pro konstrukci stromů minimálního překlenutí daného připojeného grafu . Vždy najdou optimální řešení, které obecně nemusí být jedinečné.

Viz také

Reference

Prameny

externí odkazy

• „Greedy Algoritmus“ , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Dárek, Noah. „Příklad chamtivé mince Python“ .