Hilbertova transformace - Hilbert transform

V matematice a při zpracování signálu je Hilbertova transformace specifický lineární operátor, který přebírá funkci, $u (t)$ skutečné proměnné a vytváří další funkci skutečné proměnné $H (u) (t)$ . Tento lineární operátor je dán konvolucí s funkcí (viz § Definice ). Hilbertova transformace má obzvláště jednoduchou reprezentaci ve frekvenční oblasti : Přináší fázový posun ± 90 ° ( $π$ ⁄ 2 radiány) každé frekvenční složce funkce, znaménko posunu v závislosti na znaménku frekvence (viz § Vztah s Fourierovou transformací ). Hilbertova transformace je důležitá při zpracování signálu, kde je součástí analytické reprezentace signálu s reálnou hodnotou $u$ $($ $t$ $)$ . Hilbertovu transformaci poprvé představil David Hilbert v tomto prostředí, aby vyřešil speciální případ problému Riemann – Hilbert pro analytické funkce. ${\ Displaystyle 1/(\ pi t)}$

Definice

Hilbertovy transformace $u$ si lze představit jako konvoluce o $u (t)$ se funkce $h ( t ) =.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 1/ π t$ , známý jako jádro Cauchy . Protože 1 / $t$ není integrovatelný napříč $t = 0$ , integrál definující konvoluci nemusí vždy konvergovat. Místo toho je Hilbertova transformace definována pomocí hlavní hodnoty Cauchy (zde zde označena $pv$ ). Hilbertova transformace funkce (nebo signálu) $u (t)$ je explicitně dána vztahem

{\ displaystyle \ operatorname {H} (u) (t) = {\ frac {1} {\ pi}} \, \ operatorname {pv} \ int _ {-\ infty}^{+\ infty} {\ frac {u (\ tau)} {t- \ tau}} \; \ mathrm {d} \ tau,}

za předpokladu, že tento integrál existuje jako hlavní hodnota. To je právě konvoluce $u$ s temperovaným rozdělením $p.v. 1 / π t$ . Alternativně lze změnou proměnných integrál hlavní hodnoty zapsat explicitně jako

{\ Displaystyle \ operatorname {H} (u) (t) =-{\ frac {1} {\, \ pi \,}} \, \ lim _ {\ varepsilon \ to 0} \, \ int _ {\ varepsilon}^{\ infty} {\ frac {\, u (t+\ tau) -u (t- \ tau) \,} {\ tau}} \; \ mathrm {d} \ tau ~.}

Když se Hilbertova transformace aplikuje dvakrát za sebou na funkci $u$ , výsledek je záporný $u$ :

{\ displaystyle \ operatorname {H} {\ bigl (} \ operatorname {H} (u) {\ bigr)} (t) =-u (t),}

za předpokladu, že integrály definující obě iterace konvergují ve vhodném smyslu. Zejména je inverzní transformace $-H$ . Tuto skutečnost lze nejsnadněji zjistit zvážením účinku Hilbertovy transformace na Fourierovu transformaci $u (t)$ (viz § Vztah s Fourierovou transformací , níže).

Pro analytickou funkci v horní polorovině popisuje Hilbertova transformace vztah mezi skutečnou částí a imaginární částí hraničních hodnot. To znamená, že pokud $f (z)$ je analytický v horní poloviční komplexní rovině ${z : Im {z}> 0}$ , a $u (t) = Re {f (t + 0 \cdot i)}$ , pak $Im {f (t + 0 \cdot i)} = H (u) (t)$ až do aditivní konstanty za předpokladu, že tato Hilbertova transformace existuje.

Zápis

Při zpracování signálu je Hilbertova transformace $u (t)$ běžně označována . V matematice je však tento zápis již široce používán k označení Fourierovy transformace $u$ $($ $t$ $)$ . Občas může být Hilbertova transformace označena . Kromě toho mnoho zdrojů definuje Hilbertovu transformaci jako negativum zde definovaného. ${\ displaystyle {\ hat {u}} (t)}$ ${\ displaystyle {\ tilde {u}} (t)}$

Dějiny

Hilbertova transformace vznikla v Hilbertově práci z roku 1905 na problému, který Riemann představoval v souvislosti s analytickými funkcemi, kterému se začalo říkat problém Riemann – Hilbert . Hilbertova práce se zabývala hlavně Hilbertovou transformací pro funkce definované na kruhu. Některé z jeho dřívějších prací souvisejících s diskrétní transformací Hilberta pocházejí z přednášek, které měl v Göttingenu . Výsledky později publikoval Hermann Weyl ve své disertační práci. Schur vylepšil Hilbertovy výsledky o diskrétní Hilbertově transformaci a rozšířil je na integrální případ. Tyto výsledky byly omezeny na mezery $L 2$ a $ℓ 2$ . V roce 1928, Marcel Riesz prokázáno, že Hilbertova transformace mohou být definovány pro u v ( L ^p prostoru ) pro $1 <$ $p$ $<\infty$ , že Hilbertova transformace je ohraničený operátor na dobu $1 <$ $p$ $<\infty$ , a že podobné výsledky držet pro Hilbertova transformace na kruhu, stejně jako diskrétní Hilbertova transformace. Hilbertova transformace byla motivujícím příkladem pro Antonia Zygmunda a Alberta Calderóna při studiu singulárních integrálů . Jejich vyšetřování hrálo zásadní roli v moderní harmonické analýze. Různé zobecnění Hilbertovy transformace, jako jsou bilineární a trilineární Hilbertovy transformace, jsou dnes stále aktivní oblastí výzkumu. ${\ Displaystyle L^{p} (\ mathbb {R})}$ ${\ Displaystyle L^{p} (\ mathbb {R})}$

Vztah k Fourierově transformaci

Hilbertova transformace je operátor multiplikátoru . Násobitel $H$ je $σ H (ω) = - i sgn (ω)$ , kde $sgn$ je funkce signum . Proto:

{\ displaystyle {\ mathcal {F}} {\ bigl (} \ operatorname {H} (u) {\ bigr)} (\ omega) =-i \ operatorname {sgn} (\ omega) \ cdot {\ mathcal { F}} (u) (\ omega),}

kde označuje Fourierovu transformaci . Protože $sgn ($ $x$ $) = sgn (2$ $π$ $x$ $)$ , vyplývá, že tento výsledek platí pro tři společné definice . ${\ displaystyle {\ mathcal {F}}}$ ${\ displaystyle {\ mathcal {F}}}$

Tím, Eulerovy rovnice ,

{\ displaystyle \ sigma _ {\ operatorname {H}} (\ omega) = {\ begin {cases} ~~ i = e^{+{\ frac {i \ pi} {2}}}, & {\ text {for}} \ omega <0, \\ ~~ 0, & {\ text {for}} \ omega = 0, \\-i = e^{-{\ frac {i \ pi} {2}}} , & {\ text {for}} \ omega> 0. \ end {cases}}}

Proto $H (u) (t)$ má účinek posunutí fáze negativních frekvenčních složek $u (t)$ o +90 ° ( $π$ ⁄ 2 radiány) a fáze pozitivních frekvenčních složek o -90 °, a $i \cdot H (u) (t)$ má za následek obnovení pozitivních frekvenčních složek při posunutí negativních frekvenčních složek o dalších +90 °, což má za následek jejich negaci (tj. násobení −1).

Když se Hilbertova transformace aplikuje dvakrát, fáze záporné a kladné frekvenční složky $u (t)$ se posunou o +180 ° a -180 °, což jsou ekvivalentní množství. Signál je negován; tj. $H (H (u)) = - u$ , protože

{\ displaystyle {\ bigl (} \ sigma _ {\ operatorname {H}} (\ omega) {\ bigr)}^{2} = e^{\ pm i \ pi} =-1 \ quad {\ text { pro}} \ omega \ neq 0.}

Tabulka vybraných Hilbertových transformací

V následující tabulce je parametr frekvence skutečný. ${\ displaystyle \ omega}$

Signál ${\ displaystyle u (t)}$	Hilbertova transformace ${\ displaystyle \ operatorname {H} (u) (t)}$
${\ Displaystyle \ sin (\ omega t)}$	${\ Displaystyle {\ begin {array} {lll} \ sin \ left (\ omega t-{\ tfrac {\ pi} {2}} \ right), \ quad \ omega> 0 \\\ sin \ left (\ omega t+{\ tfrac {\ pi} {2}} \ right), \ quad \ omega <0 \ end {array}}}$
${\ displaystyle \ cos (\ omega t)}$	${\ Displaystyle {\ begin {array} {lll} \ cos \ left (\ omega t-{\ tfrac {\ pi} {2}} \ right), \ quad \ omega> 0 \\\ cos \ left (\ omega t+{\ tfrac {\ pi} {2}} \ right), \ quad \ omega <0 \ end {array}}}$
${\ displaystyle e^{i \ omega t}}$	${\ displaystyle {\ begin {array} {lll} e^{i \ left (\ omega t-{\ tfrac {\ pi} {2}} \ right)}, \ quad \ omega> 0 \\ e^{ i \ left (\ omega t+{\ tfrac {\ pi} {2}} \ right)}, \ quad \ omega <0 \ end {array}}}$
${\ Displaystyle e^{-i \ omega t}}$	${\ displaystyle {\ begin {array} {lll} e^{-i \ left (\ omega t-{\ tfrac {\ pi} {2}} \ right)}, \ quad \ omega> 0 \\ e^ {-i \ left (\ omega t+{\ tfrac {\ pi} {2}} \ right)}, \ quad \ omega <0 \ end {array}}}$
${\ displaystyle 1 \ over t^{2} +1}$	${\ displaystyle t \ over t^{2} +1}$
${\ displaystyle e^{-t^{2}}}$	${\ displaystyle {\ frac {2} {\ sqrt {\ pi \,}}} F (t)}$ (viz Dawsonova funkce )
Funkce zinku ${\ Displaystyle \ sin (t) \ over t}$	${\ Displaystyle 1- \ cos (t) \ over t}$
Funkce Dirac delta ${\ Displaystyle \ delta (t)}$	${\ displaystyle {1 \ over \ pi t}}$
Charakteristická funkce ${\ Displaystyle \ chi _ {[a, b]} (t)}$	${\ Displaystyle {{\ frac {1} {\, \ pi \,}} \ ln \ left \ vert {\ frac {ta} {tb}} \ right \ vert}}$

Poznámky

^ Někteří autoři (např. Bracewell) používajíjako definici dopředné transformacenaše $-H$ . Důsledkem je, že pravý sloupec této tabulky bude negován.
^ ^a ^b Hilbertovu transformaci funkcí sin a cos lze definovat tak, že vezmeme hlavní hodnotu integrálu v nekonečnu. Tato definice souhlasí s výsledkem distribuční definice Hilbertovy transformace.

K dispozici je rozsáhlá tabulka Hilbertových transformací. Všimněte si, že Hilbertova transformace konstanty je nulová.

Definiční doména

V žádném případě není zřejmé, že Hilbertova transformace je vůbec dobře definována, protože nesprávný integrál definující ji musí ve vhodném smyslu konvergovat. Hilbertova transformace je však dobře definována pro širokou třídu funkcí, jmenovitě pro $1 <$ $p$ $<\infty$ . ${\ Displaystyle L^{p} (\ mathbb {R})}$

Přesněji, pokud $u$ je pro $1 <$ $p$ $<\infty$ , pak mez definující nevlastní integrál ${\ Displaystyle L^{p} (\ mathbb {R})}$

{\ displaystyle \ operatorname {H} (u) (t) =-{\ frac {1} {\ pi}} \ lim _ {\ varepsilon \ to 0} \ int _ {\ varepsilon}^{\ infty} { \ frac {u (t+\ tau) -u (t- \ tau)} {\ tau}} \, d \ tau}

existuje téměř pro každé $t$ . Mezní funkce je také in a je ve skutečnosti mezní hodnotou v průměru nesprávného integrálu. To znamená, ${\ Displaystyle L^{p} (\ mathbb {R})}$

{\ Displaystyle-{\ frac {1} {\ pi}} \ int _ {\ varepsilon}^{\ infty} {\ frac {u (t+\ tau) -u (t- \ tau)} {\ tau} } \, \ mathrm {d} \ tau \ to \ operatorname {H} (u) (t)}

jako $ε \to 0$ v normě $L p$ , stejně jako bodově téměř všude, podle Titchmarshovy věty .

V případě $p = 1$ se Hilbertova transformace stále bodově sbíhá téměř všude, ale sama o sobě nemusí být integrovatelná, a to ani lokálně. Zejména konvergence průměru v tomto případě obecně nenastává. Hilbertova transformace funkce $L 1 se$ však sbíhá v $L 1$ -slabá a Hilbertova transformace je omezený operátor od $L 1$ do $L 1, w$ . (Zejména, protože Hilbertova transformace je také operátorem multiplikátoru na $L 2$ , Marcinkiewiczova interpolace a argument duality poskytují alternativní důkaz, že $H$ je ohraničeno na $L p$ .)

Vlastnosti

Ohraničenost

Pokud $1 < p <\infty$ , pak Hilbertova transformace je omezený lineární operátor , což znamená, že existuje konstantní $C$ $p$ taková, že ${\ Displaystyle L^{p} (\ mathbb {R})}$

{\ displaystyle \ left \ | \ operatorname {H} u \ right \ | _ {p} \ leq C_ {p} \ left \ | u \ right \ | _ {p}}

pro všechny . ${\ Displaystyle u \ in L^{p} (\ mathbb {R})}$

Nejlepší konstanta je dána vztahem ${\ displaystyle C_ {p}}$

{\ Displaystyle C_ {p} = {\ begin {cases} \ tan {\ frac {\ pi} {2p}} & {\ text {for}} ~ 1 <p \ leq 2 \\\ cot {\ frac { \ pi} {2p}} & {\ text {for}} ~ 2 <p <\ infty \ end {cases}}}

Snadný způsob, jak najít to nejlepší pro sílu 2, je prostřednictvím takzvané Cotlarovy identity, která pro všechny skutečné hodnotné $f$ . Stejné nejlepší konstanty platí pro periodickou Hilbertovu transformaci. ${\ displaystyle C_ {p}}$ ${\ displaystyle p}$ ${\ displaystyle (\ operatorname {H} f)^{2} = f^{2} +2 \ operatorname {H} (f \ operatorname {H} f)}$

Ohraničenost Hilbertovy transformace předpokládá konvergenci operátoru symetrického částečného součtu ${\ Displaystyle L^{p} (\ mathbb {R})}$

{\ Displaystyle S_ {R} f = \ int _ {-R}^{R} {\ hat {f}} (\ xi) e^{2 \ pi ix \ xi} \, \ mathrm {d} \ xi }

na $f$ v . ${\ Displaystyle L^{p} (\ mathbb {R})}$

Anti-self adjpointness

Hilbertova transformace je anti- self adjoint operátor ve vztahu k dualitnímu párování mezi a duálním prostorem , kde $p$ a $q$ jsou Hölderovy konjugáty a $1 <$ $p$ $,$ $q$ $<\infty$ . Symbolicky, ${\ Displaystyle L^{p} (\ mathbb {R})}$ ${\ Displaystyle L^{q} (\ mathbb {R})}$

{\ displaystyle \ langle \ operatorname {H} u, v \ rangle = \ langle u,-\ operatorname {H} v \ rangle}

pro a . ${\ Displaystyle u \ in L^{p} (\ mathbb {R})}$ ${\ Displaystyle v \ in L^{q} (\ mathbb {R})}$

Inverzní transformace

Hilbertova transformace je antiinvoluce , to znamená

{\ displaystyle \ operatorname {H} {\ bigl (} \ operatorname {H} \ left (u \ right) {\ bigr)} =-u}

za předpokladu, že každá transformace je dobře definována. Protože $H$ zachovává prostor , znamená to zejména, že Hilbertova transformace je invertibilní na , a to ${\ Displaystyle L^{p} (\ mathbb {R})}$ ${\ Displaystyle L^{p} (\ mathbb {R})}$

{\ displaystyle \ operatorname {H} ^{-1} =-\ operatorname {H}}

Složitá struktura

Protože $H 2 = -I$ („ $I$ “ je operátor identity ) ve skutečném Banachově prostoru funkcí s reálným hodnocením , definuje Hilbertova transformace lineární komplexní strukturu v tomto Banachově prostoru. Zejména, když $p$ $= 2$ , Hilbertova transformace dává Hilbertovi prostor skutečných funkcí ve struktuře komplexního Hilbertova prostoru. ${\ Displaystyle L^{p} (\ mathbb {R})}$ ${\ Displaystyle L^{2} (\ mathbb {R})}$

(Komplexní) vlastní stavy Hilbertovy transformace připouštějí reprezentace jako holomorfní funkce v horní a dolní polorovině v Hardyho prostoru $H 2$ podle Paley-Wienerovy věty .

Diferenciace

Formálně je derivátem Hilbertovy transformace Hilbertova transformace derivátu, tj. Tyto dva lineární operátory dojíždějí:

{\ displaystyle \ operatorname {H} \ left ({\ frac {\ mathrm {d} u} {\ mathrm {d} t}} \ right) = {\ frac {\ mathrm {d}} {\ mathrm {d } t}} \ operatorname {H} (u)}

Iterace této identity,

{\ displaystyle \ operatorname {H} \ left ({\ frac {\ mathrm {d} ^{k} u} {\ mathrm {d} t ^{k}}} \ right) = {\ frac {\ mathrm { d} ^{k}} {\ mathrm {d} t ^{k}}} \ operatorname {H} (u)}

To je přesně pravda, jak je uvedeno za předpokladu, že $u$ a jeho prvních $k$ derivátů patří . Lze to snadno zkontrolovat ve frekvenční oblasti, kde se z diferenciace stává násobení $ω$ . ${\ Displaystyle L^{p} (\ mathbb {R})}$

Konvoluce

Hilbertovu transformaci lze formálně realizovat jako konvoluci s temperovanou distribucí

{\ displaystyle h (t) = \ operatorname {pv} {\ frac {1} {\ pi \, t}}}

Formálně tedy

{\ displaystyle \ operatorname {H} (u) = h*u}

Nicméně, a priori, to může být definována pouze $u$ distribuci kompaktním nosičem . Je možné s tím pracovat poněkud přísně, protože kompaktně podporované funkce (což jsou distribuce a fortiori ) jsou v $L$ $p$ husté . Alternativně lze použít skutečnost, že h ( t ) je distribuční derivát funkce $log |$ $t$ $|/$ $π$ ; vtipkovat

{\ displaystyle \ operatorname {H} (u) (t) = {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ left ({\ frac {1} {\ pi}} \ left (u*\ log {\ bigl |} \ cdot {\ bigr |} \ right) (t) \ right)}

Pro většinu operačních účelů lze Hilbertovu transformaci považovat za konvoluci. Například ve formálním smyslu je Hilbertova transformace konvoluce konvolucí Hilbertovy transformace aplikované pouze na jeden z těchto faktorů:

{\ displaystyle \ operatorname {H} (u*v) = \ operatorname {H} (u)*v = u*\ operatorname {H} (v)}

To platí přesně, pokud $u$ a $v$ jsou kompaktně podporované distribuce, protože v takovém případě

{\ Displaystyle h*(u*v) = (h*u)*v = u*(h*v)}

Při přechodu na vhodnou mez je tedy také pravdivé, pokud $u \in L p$ a $v \in L q$ za předpokladu, že

{\ displaystyle 1 <{\ frac {1} {p}}+{\ frac {1} {q}}}

z věty kvůli Titchmarshovi.

Neměnnost

Hilbertova transformace má následující vlastnosti invariance . ${\ Displaystyle L^{2} (\ mathbb {R})}$

Dojíždí s překlady. To znamená, že dojíždí s operátory $T a f (x) = f (x + a)$ pro všechny $a$ in ${\ displaystyle \ mathbb {R}.}$
Dojíždí pozitivními dilatacemi. To znamená, že dojíždí s operátory $M λ f (x) = f (λ x)$ pro všechny $λ > 0$ .
To anticommutes s odrazem $R f (x) = f (- x)$ .

Až do multiplikativní konstanty je Hilbertova transformace jediným omezeným operátorem na $L$ ² s těmito vlastnostmi.

Ve skutečnosti existuje širší soubor operátorů, kteří dojíždějí s Hilbertovou transformací. Skupina působí pomocí unitárních operátorů $U$ $g$ na prostor podle vzorce ${\ displaystyle {\ text {SL}} (2, \ mathbb {R})}$ ${\ Displaystyle L^{2} (\ mathbb {R})}$

{\ displaystyle \ operatorname {U} _ {g}^{-1} f (x) = {\ frac {1} {cx+d}} \, f \ left ({\ frac {ax+b} {cx +d}} \ right) \ ,, \ qquad g = {\ begin {bmatrix} a & b \\ c & d \ end {bmatrix}} ~, \ qquad {\ text {for}} ~ ad-bc = \ pm 1. }

Tato unitární reprezentace je příkladem hlavní sériovou zastoupení všech v tomto případě je redukovat, rozdělení jako ortogonální součet dvou invariantních podprostorů, Hardy prostoru a jeho konjugátu. Jedná se o prostory hraničních hodnot $L$ $2$ holomorfních funkcí na horní a dolní polorovině. a jeho konjugát sestává přesně z těch funkcí $L$ $2$ s Fourierovými transformacemi mizícími na záporných a kladných částech skutečné osy. Vzhledem k tomu, Hilbertova transformace se rovná $H = -$ $i$ $(2$ $P$ $- I)$ , přičemž $P$ je kolmý průmět z na a $I$ operátor identity , to znamená, že i jeho kolmé jsou eigenspaces z $H$ pro vlastní čísla $\pm$ $i$ . Jinými slovy, $H$ dojíždí s operátory $U$ $g$ . Omezení operátorů $U$ $g$ to a jeho konjugátu poskytují neredukovatelné reprezentace -takzvaného limitu reprezentací diskrétních sérií . ${\ displaystyle ~ {\ text {SL}} (2, \ mathbb {R}) ~.}$ ${\ Displaystyle H^{2} (\ mathbb {R})}$ ${\ Displaystyle H^{2} (\ mathbb {R})}$ ${\ Displaystyle L^{2} (\ mathbb {R})}$ ${\ displaystyle \ operatorname {H} ^{2} (\ mathbb {R}),}$ ${\ displaystyle \ operatorname {H} ^{2} (\ mathbb {R})}$ ${\ displaystyle \ operatorname {H} ^{2} (\ mathbb {R})}$ ${\ displaystyle {\ text {SL}} (2, \ mathbb {R})}$

Rozšíření definiční domény

Hilbertova transformace distribucí

Dále je možné rozšířit Hilbertovu transformaci do určitých distribučních prostorů ( Pandey 1996 , kapitola 3). Vzhledem k tomu, Hilbertova transformace dojíždí s diferenciací, a je ohraničený operátor na $L p$ , $H$ omezuje, aby kontinuální transformace na inverzní limitu z Soboleových prostorů :

{\ displaystyle {\ mathcal {D}} _ {L^{p}} = {\ underset {n \ to \ infty} {\ underset {\ longleftarrow} {\ lim}}} W^{n, p} ( \ mathbb {R})}

Hilbertovu transformaci pak lze definovat na duálním prostoru , označeném , sestávajícím z distribucí $L$ $p$ . Toho je dosaženo pomocí duality párování: U , definujeme: ${\ displaystyle {\ mathcal {D}} _ {L^{p}}}$ ${\ displaystyle {\ mathcal {D}} _ {L^{p}} '}$
${\ displaystyle u \ in {\ mathcal {D}} '_ {L^{p}}}$

{\ displaystyle \ operatorname {H} (u) \ in {\ mathcal {D}} '_ {L^{p}} = \ langle \ operatorname {H} u, v \ rangle \ \ triangleq \ \ langle u, -\ operatorname {H} v \ rangle, \ {\ text {for all}} \ v \ in {\ mathcal {D}} _ {L^{p}}.}

Je možné definovat Hilbertovu transformaci na prostoru temperovaných distribucí také přístupem díky Gel'fandovi a Shilovovi, ale vzhledem k singularitě v integrálu je zapotřebí podstatně větší péče.

Hilbertova transformace ohraničených funkcí

Hilbertovu transformaci lze definovat i pro funkce , ale vyžaduje určité úpravy a upozornění. Správně pochopen, Hilbertovy transformace mapy do Banachova prostoru z ohraničené střední oscilace (BMO) tříd. ${\ Displaystyle L^{\ infty} (\ mathbb {R})}$ ${\ Displaystyle L^{\ infty} (\ mathbb {R})}$

Hilbertova transformace ohraničené funkce, vykládaná naivně, je jasně špatně definována. Například s $u = sgn (x)$ se integrál definující $H (u)$ rozchází téměř všude na $\pm \infty$ . Ke zmírnění těchto obtíží je proto Hilbertova transformace funkce $L \infty$ definována následující regularizovanou formou integrálu

{\ displaystyle \ operatorname {H} (u) (t) = \ operatorname {pv} \ int _ {-\ infty}^{\ infty} u (\ tau) \ left \ {h (t- \ tau)- h_ {0} (-\ tau) \ vpravo \} \, \ mathrm {d} \ tau}

kde jak výše $h (x) = 1 / πx$ a

{\ displaystyle h_ {0} (x) = {\ begin {cases} 0 & {\ text {for}} ~ | x | <1 \\ {\ frac {1} {\ pi \, x}} & {\ text {for}} ~ | x | \ geq 1 \ end {cases}}}

Upravená transformace $H$ souhlasí s původní transformací funkcí kompaktní podpory z obecného výsledku Calderóna a Zygmunda. Výsledný integrál navíc bodově konverguje téměř všude a s ohledem na normu BMO na funkci omezené střední oscilace.

Hluboký výsledek z Fefferman práce je, že funkce je ohraničené střední kmitání pouze v případě, že má formu $f$ $+ H ($ $g$ $)$ pro některé . ${\ Displaystyle f, g \ in L^{\ infty} (\ mathbb {R})}$

Funkce konjugátu

Hilbertovu transformaci lze chápat jako dvojici funkcí $f (x)$ a $g (x)$ tak, že funkce

{\ Displaystyle F (x) = f (x)+i \, g (x)}

je hraniční hodnota holomorfní funkce

F (z)

v horní polorovině. Za těchto okolností, pokud jsou

f

a

g

dostatečně integrovatelné, pak jeden je Hilbertova transformace druhého.

Předpokládejme, že pak, podle teorie Poissonova integrálu , $f$ připouští jedinečný harmonické rozšíření do horní polorovině, a toto rozšíření je dána ${\ Displaystyle f \ in L^{p} (\ mathbb {R}).}$

{\ Displaystyle u (x+iy) = u (x, y) = {\ frac {1} {\ pi}} \ int _ {-\ infty}^{\ infty} f (s) \; {\ frac {y} {(xs)^{2}+y^{2}}} \; \ mathrm {d} s}

což je konvoluce $f$ s Poissonovým jádrem

{\ Displaystyle P (x, y) = {\ frac {y} {\ pi \, \ left (x^{2}+y^{2} \ right)}}}

Kromě toho existuje v horní polorovině jedinečná harmonická funkce $v$ definovaná tak, že $F (z) = u (z) + iv (z)$ je holomorfní a

{\ Displaystyle \ lim _ {y \ to \ infty} v \, (x+i \, y) = 0}

Tato harmonická funkce je získána z $f$ konvolucí s konjugovaným Poissonovým jádrem

{\ Displaystyle Q (x, y) = {\ frac {x} {\ pi \, \ left (x^{2}+y^{2} \ right)}}.}

Tím pádem

{\ Displaystyle v (x, y) = {\ frac {1} {\ pi}} \ int _ {-\ infty}^{\ infty} f (s) \; {\ frac {xs} {\, ( xs)^{2}+y^{2} \,}} \; \ mathrm {d} s.}

Skutečné a imaginární části jádra Cauchy skutečně jsou

{\ Displaystyle {\ frac {i} {\ pi \, z}} = P (x, y)+i \, Q (x, y)}

takže $F = u + iv$ je holomorfní podle Cauchyho integrálního vzorce .

Funkce $v$ získaný z $u$ tímto způsobem se nazývá harmonické konjugát z $u$ . (Netangenciální) hraniční limit $v (x, y)$ jako $y \to 0$ je Hilbertova transformace $f$ . Stručně tedy

{\ displaystyle \ operatorname {H} (f) = \ lim _ {y \ to 0} Q (-, y) \ star f}

Titchmarshova věta

Titchmarshova věta (pojmenovaná po EC Titchmarshovi, který ji zahrnul do své práce z roku 1937) upřesňuje vztah mezi hraničními hodnotami holomorfních funkcí v horní polorovině a Hilbertovou transformací. Poskytuje nezbytné a dostatečné podmínky, aby komplexně oceněná funkce integrovatelná do čtverce $F (x)$ na reálné přímce byla hraniční hodnotou funkce v Hardyho prostoru $H 2 (U)$ holomorfních funkcí v horní polorovině $U$ .

Věta uvádí, že následující podmínky pro komplexně integrovanou funkci čtvercově integrovatelné jsou ekvivalentní: ${\ Displaystyle F: \ mathbb {R} \ to \ mathbb {C}}$

$F (x)$ je limita $z \to x$ holomorfní funkce $F (z)$ v horní polorovině tak, že ${\ Displaystyle \ int _ {-\ infty}^{\ infty} | F (x+i \, y) |^{2} \; \ mathrm {d} x <K}$
Skutečné a imaginární části $F (x)$ jsou Hilbertovy transformace navzájem.
Fourierova transformace zmizí pro $x$ $<0$ . ${\ displaystyle {\ mathcal {F}} (F) (x)}$

Slabší výsledek platí pro funkce třídy $L p$ pro $p > 1$ . Konkrétně, pokud $F (z)$ je holomorfní funkce taková, že

{\ Displaystyle \ int _ {-\ infty}^{\ infty} | F (x+i \, y) |^{p} \; \ mathrm {d} x <K}

pro všechna $y$ pak existuje komplexně hodnocená funkce $F (x)$ v tom smyslu, že $F$ $($ $x$ $+$ $iy$ $) \to$ $F$ $($ $x$ $)$ v $L$ $p$ normě jako $y$ $\to 0$ (stejně jako bodové držení téměř všude ). Kromě toho, ${\ Displaystyle L^{p} (\ mathbb {R})}$

{\ Displaystyle F (x) = f (x) -i \, g (x)}

kde $f$ je funkce se skutečnou hodnotou in a $g$ je Hilbertova transformace (třídy $L$ $p$ ) $f$ . ${\ Displaystyle L^{p} (\ mathbb {R})}$

To neplatí v případě $p = 1$ . Ve skutečnosti, Hilbertova transformace z $L 1,$ funkce $f$ potřeby nekonverguje v střední k jinému $L 1$ funkci. Nicméně Hilbertova transformace $f$ konverguje téměř všude na konečnou funkci $g$ tak, že

{\ Displaystyle \ int _ {-\ infty}^{\ infty} {\ frac {| g (x) |^{p}} {1+x^{2}}} \; \ mathrm {d} x < \ infty}

Tento výsledek je přímo analogický výsledku Andreyho Kolmogorova pro Hardyho funkce na disku. Ačkoli se obvykle nazývá Titchmarshova věta, výsledek agreguje mnoho práce ostatních, včetně Hardyho, Paleyho a Wienera (viz Paley -Wienerova věta ), stejně jako práce Riesze, Hille a Tamarkina

Problém Riemann – Hilbert

Jedna forma problému Riemann – Hilbert se snaží identifikovat páry funkcí $F +$ a $F -$ takové, že $F +$ je holomorfní v horní polorovině a $F -$ je holomorfní v dolní polorovině, takže pro $x$ podél skutečné osa,

{\ displaystyle F _ {+} (x) -F _ {-} (x) = f (x)}

kde $f (x)$ je nějaká daná funkce s reálnou hodnotou . Levou stranu této rovnice lze chápat buď jako rozdíl mezí $F$ $\pm$ od příslušných polorovin, nebo jako distribuci hyperfunkce . Dvě funkce této formy jsou řešením problému Riemann – Hilbert. ${\ displaystyle x \ in \ mathbb {R}}$

Formálně, pokud $F \pm$ vyřeší problém Riemann – Hilbert

{\ Displaystyle f (x) = F _ {+} (x) -F _ {-} (x)}

potom je Hilbertova transformace $f (x)$ dána vztahem

{\ Displaystyle H (f) (x) =-i {\ bigl (} F _ {+} (x)+F _ {-} (x) {\ bigr)}.}

Hilbertova transformace na kruhu

Pro periodickou funkci $f$ je definována kruhová Hilbertova transformace:

{\ displaystyle {\ tilde {f}} (x) \ triangleq {\ frac {1} {2 \ pi}} \ operatorname {pv} \ int _ {0}^{2 \ pi} f (t) \, \ cot \ left ({\ frac {xt} {2}} \ right) \, \ mathrm {d} t}

Kruhová Hilbertova transformace se používá při charakterizaci Hardyho prostoru a při studiu konjugované funkce ve Fourierově řadě. Jádro,

{\ displaystyle \ cot \ left ({\ frac {xt} {2}} \ right)}

je známý jako Hilbertovo jádro, protože v této podobě byla původně studována Hilbertova transformace.

Hilbertovo jádro (pro kruhovou Hilbertovu transformaci) lze získat tak, že Cauchyho jádro bude 1 / $x$ periodické. Přesněji pro $x \neq 0$

{\ Displaystyle {\ frac {1} {\, 2 \,}} \ cot \ left ({\ frac {x} {2}} \ right) = {\ frac {1} {x}}+\ sum _ {n = 1}^{\ infty} \ left ({\ frac {1} {x+2n \ pi}}+{\ frac {1} {\, x-2n \ pi \,}} \ right)}

Mnoho výsledků o kruhové Hilbertově transformaci lze odvodit z odpovídajících výsledků pro Hilbertovu transformaci z této korespondence.

Další přímější spojení poskytuje Cayleyova transformace $C (x) = (x - i) / (x + i)$ , která nese skutečnou přímku na kruh a horní polovinu roviny na disk jednotky. Vyvolává unitární mapu

{\ Displaystyle U \, f (x) = {\ frac {1} {(x+i) \, {\ sqrt {\ pi}}}} \, f \ left (C \ left (x \ right) \ že jo)}

z $L 2 (T)$ na Provozovatel $U$ nese Hardyho prostor $H$ $2$ $($ $T$ $)$ na Hardy prostoru . ${\ Displaystyle L^{2} (\ mathbb {R}).}$ ${\ Displaystyle H^{2} (\ mathbb {R})}$

Hilbertova transformace při zpracování signálu

Bedrosianova věta

Bedrosianova věta uvádí, že Hilbertova transformace součinu nízkoprůchodového a vysokoprůchodového signálu s nepřekrývajícími se spektry je dána součinem nízkoprůchodového signálu a Hilbertovy transformace horního průchodu, popř.

{\ displaystyle \ operatorname {H} \ left (f _ {\ text {LP}} (t) \ cdot f _ {\ text {HP}} (t) \ right) = f _ {\ text {LP}} (t) \ cdot \ operatorname {H} \ left (f _ {\ text {HP}} (t) \ right),}

kde $f LP$ a $f HP$ jsou signály dolního a vysokého průchodu. Kategorie komunikačních signálů, na které se to vztahuje, se nazývá model úzkopásmového signálu. Členem této kategorie je amplitudová modulace vysokofrekvenčního sinusového „nosiče“:

{\ Displaystyle u (t) = u_ {m} (t) \ cdot \ cos (\ omega t+\ phi),}

kde $u m (t)$ je tvar vlny „zprávy“ s úzkou šířkou pásma, například hlas nebo hudba. Potom podle Bedrosianovy věty:

{\ displaystyle \ operatorname {H} (u) (t) = u_ {m} (t) \ cdot \ sin (\ omega t+\ phi).}

Analytická reprezentace

Specifický typ konjugované funkce je :

{\ Displaystyle u_ {a} (t) \ triangleq u (t)+i \ cdot H (u) (t),}

známý jako analytické reprezentace z The jméno ukazuje jeho matematický povolnost, převážně v důsledku Eulerovy rovnice . Při použití Bedrosianovy věty na úzkopásmový model je analytická reprezentace : ${\ Displaystyle u (t).}$

{\ Displaystyle {\ begin {aligned} u_ {a} (t) & = u_ {m} (t) \ cdot \ cos (\ omega t+\ phi)+i \ cdot u_ {m} (t) \ cdot \ sin (\ omega t+\ phi) \\ & = u_ {m} (t) \ cdot \ left [\ cos (\ omega t+\ phi)+i \ cdot \ sin (\ omega t+\ phi) \ right] \ \ & = u_ {m} (t) \ cdot e^{i (\ omega t+\ phi)}. \, \ end {zarovnáno}}}

( Rovnice 1 )

Vlastnost Fourierovy transformace naznačuje, že tato složitá heterodynní operace může posunout všechny negativní frekvenční složky $u m (t)$ nad 0 Hz. V takovém případě je imaginární částí výsledku Hilbertova transformace skutečné části. Toto je nepřímý způsob produkce Hilbertových transformací.

Úhlová (fázová/frekvenční) modulace

Formulář:

{\ Displaystyle u (t) = A \ cdot \ cos (\ omega t+\ phi _ {m} (t))}

se nazývá úhlová modulace , která zahrnuje fázovou i frekvenční modulaci . Okamžitý kmitočet je pro dostatečně velké $W$ , ve srovnání s : ${\ Displaystyle \ omega +\ phi _ {m}^{\ prime} (t).}$ ${\ Displaystyle \ phi _ {m}^{\ prime}}$

{\ displaystyle \ operatorname {H} (u) (t) \ zhruba A \ cdot \ sin (\ omega t+\ phi _ {m} (t))}

a:

{\ Displaystyle u_ {a} (t) \ zhruba A \ cdot e^{i (\ omega t+\ phi _ {m} (t))}.}

Modulace jednoho postranního pásma (SSB)

Když $u m (t)$ v Eq.1 je také analytická reprezentace (tvaru vlny zprávy), to je:

{\ Displaystyle u_ {m} (t) = m (t)+i \ cdot {\ widehat {m}} (t)}

výsledkem je jednostranná modulace pásma :

{\ Displaystyle u_ {a} (t) = (m (t)+i \ cdot {\ widehat {m}} (t)) \ cdot e^{i (\ omega t+\ phi)}}

jehož přenášenou složkou je:

{\ Displaystyle {\ begin {aligned} u (t) & = \ operatorname {Re} \ {u_ {a} (t) \} \\ & = m (t) \ cdot \ cos (\ omega t+\ phi) -{\ widehat {m}} (t) \ cdot \ sin (\ omega t+\ phi) \ end {aligned}}}

Kauzalita

Tato funkce představuje dvě výzvy praktické implementace jako konvoluci: ${\ Displaystyle h (t) = 1/(\ pi t)}$

Jeho trvání je nekonečné (technicky nekonečná podpora ). Místo toho je nutné použít aproximaci konečné délky. Ale okenních délku také snižuje účinný dosah frekvenční transformace. Čím kratší je okno, tím větší jsou ztráty na nízkých a vysokých frekvencích. Viz také kvadraturní filtr .
Je to nekauzální filtr . Je tedy vyžadována opožděná verze . Odpovídající výstup je následně zpožděn Při vytváření imaginární části analytického signálu musí být zdroj (skutečná část) zpožděn o ekvivalentní množství. ${\ Displaystyle h (t- \ tau),}$ ${\ displaystyle \ tau.}$

Diskrétní Hilbertova transformace

Obrázek 1 : Filtr, jehož frekvenční odezva je omezena pásmem na přibližně 95% Nyquistovy frekvence

Obrázek 2 : Hilbertův transformační filtr s vysokofrekvenční frekvenční charakteristikou

Obrázek 3 .

Obrázek 4 . Hilbertova transformace

cos (ωt)

je

sin (ωt)

. Tento obrázek ukazuje

sin (ωt)

a dvě přibližné Hilbertovy transformace vypočítané funkcí knihovny MATLAB, hilbert ()

Obrázek 5 . Diskrétní Hilbertovy transformace kosinové funkce pomocí konvoluce po částech

Pro diskrétní funkce , s diskrétního Fourierova transformace (DTFT) , a diskrétní Hilbertova transformace , DTFT ze v oblasti $-$ $π$ $<ω <$ $π$ je dána vztahem: ${\ displaystyle u [n]}$ ${\ displaystyle U (\ omega)}$ ${\ displaystyle {\ hat {u}} [n]}$ ${\ displaystyle {\ hat {u}} [n]}$

{\ displaystyle \ operatorname {DTFT} ({\ hat {u}}) = U (\ omega) \ cdot (-i \ cdot \ operatorname {sgn} (\ omega)).}

Inverzní DTFT pomocí konvoluční věty je:

{\ displaystyle {\ begin {aligned} {\ hat {u}} [n] & = {\ scriptstyle \ mathrm {DTFT} ^{-1}} (U (\ omega)) \ *\ {scriptstyle \ mathrm {DTFT} ^{-1}} (-i \ cdot \ operatorname {sgn} (\ omega)) \\ & = u [n] \ *\ {\ frac {1} {2 \ pi}} \ int _ {-\ pi}^{\ pi} (-i \ cdot \ operatorname {sgn} (\ omega)) \ cdot e^{i \ omega n} \, \ mathrm {d} \ omega \\ & = u [ n] \ *\ \ underbrace {{\ frac {1} {2 \ pi}} \ left [\ int _ {-\ pi}^{0} i \ cdot e^{i \ omega n} \, \ mathrm {d} \ omega -\ int _ {0}^{\ pi} i \ cdot e^{i \ omega n} \, \ mathrm {d} \ omega \ right]} _ {h [n]}, \ end {aligned}}}

kde

{\ Displaystyle h [n] \ \ triangleq \ {\ begin {cases} 0, & {\ text {for}} n {\ text {even}} \\ {\ frac {2} {\ pi n}} & {\ text {for}} n {\ text {odd}}, \ end {cases}}}

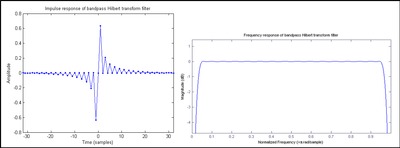
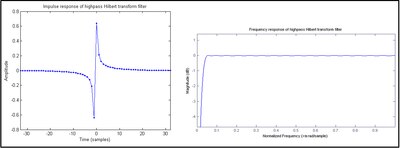
což je nekonečná impulsní reakce (IIR). Pokud je konvoluce prováděna numericky, aproximace FIR je nahrazena $h [n]$ , jak je znázorněno na obrázku 1 . FIR filtr s lichým počtem asymetrických koeficientů se nazývá typ III, který ve své podstatě vykazuje odezvy nulové velikosti na frekvencích 0 a Nyquist, což má v tomto případě za následek tvar pásmového filtru. Konstrukce typu IV (sudý počet asymetrických koeficientů) je znázorněna na obrázku 2 . Protože odezva velikosti na Nyquistově frekvenci nevypadává, přibližuje se ideálnímu Hilbertovu transformátoru o něco lépe než lichému kohoutkovému filtru. nicméně

Typická (tj. Správně filtrovaná a vzorkovaná) $u [n]$ sekvence nemá žádné užitečné složky na Nyquistově frekvenci.
Impulsní odezva typu IV vyžaduje 1 / 2 posun vzorku v sekvenci $h [n]$ . To způsobí, že se koeficienty s nulovou hodnotou stanou nenulovými, jak je vidět na obrázku 2 . Konstrukce typu III je tedy potenciálně dvakrát účinnější než typ IV.
Skupinové zpoždění návrhu typu III je celočíselný počet vzorků, což usnadňuje zarovnání s vytvořením analytického signálu . Skupinové zpoždění typu IV je na půli cesty mezi dvěma vzorky. ${\ displaystyle {\ hat {u}} [n]}$ ${\ displaystyle u [n],}$

Funkce MATLAB , hilbert (u, N) , spojuje au [n] posloupnost s periodickým součtem :

{\ Displaystyle h_ {N} [n] \ \ triangleq \ sum _ {m =-\ infty}^{\ infty} h [n-mN]}

a vrací jeden cyklus ( $N$ vzorků) periodického výsledku v imaginární části komplexní hodnotové výstupní sekvence. Konvoluce je implementována ve frekvenční oblasti jako součin pole se vzorky distribuce $-$ $i$ $sgn ($ $ω$ $)$ (jejíž skutečné a imaginární složky jsou všechny jen 0 nebo $\pm 1$ ). Obrázek 3 porovnává poloviční cyklus $h$ $N$ $[$ $n$ $]$ s ekvivalentní délkovou částí $h$ $[$ $n$ $]$ . Vzhledem k tomu, FIR aproximace pro označován náhradou za $-$ $i$ $sgn ($ $omega$ $)$ vzorky vede FIR verzi konvoluce. ${\ displaystyle {\ scriptstyle \ mathrm {DFT}} \ left (u [n] \ right)}$ ${\ Displaystyle h [n],}$ ${\ displaystyle {\ tilde {h}} [n],}$ ${\ displaystyle {\ scriptstyle \ mathrm {DFT}} \ left ({\ tilde {h}} [n] \ right)}$

Reálná část výstupního sekvence je původní vstupní sekvence tak, že komplex výstup je analytický znázornění z $u [n]$ . Když je vstupem segment čistého kosinu, výsledná konvoluce pro dvě různé hodnoty $N$ je znázorněna na obrázku 4 (červené a modré grafy). Efekty na hraně zabraňují tomu, aby byl výsledek čistě sinusová funkce (zelený plot). Protože $h N [n]$ není sekvence FIR, teoretický rozsah účinků je celá výstupní sekvence. Ale rozdíly od sinusové funkce se zmenšují se vzdáleností od okrajů. Parametr $N$ je délka výstupní sekvence. Pokud překročí délku vstupní sekvence, vstup se upraví připojením prvků s nulovou hodnotou. Ve většině případů to snižuje velikost rozdílů. Jejich trvání však dominují inherentní doby vzestupu a poklesu $h [n]$ impulzní odezvy.

Ocenění okrajových efektů je důležité, když se k provedení konvoluce na dlouhé $u$ $[$ $n$ $]$ sekvenci používá metoda zvaná overlap-save . Segmenty délky $N$ jsou spojeny s periodickou funkcí:

{\ Displaystyle {\ tilde {h}} _ {N} [n] \ \ triangleq \ sum _ {m =-\ infty}^{\ infty} {\ tilde {h}} [n-mN].}

Když doba trvání nenulových hodnot je je výstupní sekvence zahrnuje $N$ $-$ $M$ $+ 1$ vzorky $M$ $-1$ výstupů jsou vyřazeny z každého bloku $N$ a vstupní bloky se překrývají o tuto částku, aby se zabránilo mezerám. ${\ displaystyle {\ tilde {h}} [n]}$ ${\ displaystyle M <N,}$ ${\ displaystyle {\ hat {u}}.}$

Obrázek 5 je příkladem použití funkce IIR hilbert (·) a aproximace FIR. V tomto příkladu je sinusová funkce vytvořena výpočtem diskrétní Hilbertovy transformace kosinové funkce, která byla zpracována ve čtyřech překrývajících se segmentech a spojena dohromady. Jak ukazuje výsledek FIR (modrý), zkreslení patrná ve výsledku IIR (červená) nejsou způsobena rozdílem mezi $h [n]$ a $h N [n]$ (zelená a červená na obrázku 3 ). Skutečnost, že $h N [n]$ je zúžené ( okénkové ), je v této souvislosti skutečně užitečná. Skutečným problémem je, že není dostatečně oknem. Účinně $M = N$ , zatímco metoda překrývání-uložení potřebuje $M < N$ .

Číslově teoretická Hilbertova transformace

Číselná teoretická Hilbertova transformace je rozšířením diskrétní Hilbertovy transformace na celá čísla modulující příslušné prvočíslo. V tomto vyplývá zobecnění diskrétní Fourierovy transformace na číselné teoretické transformace. Hilbertovu transformaci teoretických čísel lze použít ke generování sad ortogonálních diskrétních sekvencí.

Viz také

Poznámky

Citace stránek

Reference

Bargmann, V. (1947). „Neredukovatelné unitární reprezentace Lorentzovy skupiny“. Ann. matematiky . 48 (3): 568–640. doi : 10,2307/1969129 . JSTOR 1969129 .
Bedrosian, E. (prosinec 1962). Produktová věta pro Hilbertovy transformace (PDF) (zpráva). Rand Corporation. RM-3439-PR.
Bitsadze, AV (2001) [1994], "Problémy hraničních hodnot teorie analytické funkce" , Encyklopedie matematiky , EMS Press
Bracewell, R. (2000). Fourierova transformace a její aplikace (3. vyd.). McGraw -Hill. ISBN 0-07-116043-4.
Brandwood, David (2003). Fourierovy transformace v radaru a zpracování signálu . Boston: Artech House. ISBN 9781580531740.
Calderón, AP ; Zygmund, A. (1952). „O existenci určitých singulárních integrálů“ . Acta Mathematica . 88 (1): 85–139. doi : 10,1007/BF02392130 .
Duoandikoetxea, J. (2000). Fourierova analýza . Americká matematická společnost. ISBN 0-8218-2172-5.
Duistermaat, JJ; Kolk, JAC (2010). Distribuce . Birkhäuser. doi : 10,1007/978-0-8176-4675-2 . ISBN 978-0-8176-4672-1.
Duren, P. (1970). Teorie prostorů H^p . New York, NY: Academic Press.
Fefferman, C. (1971). „Charakteristiky omezené střední oscilace“ . Bulletin Americké matematické společnosti . 77 (4): 587–588. doi : 10,1090/S0002-9904-1971-12763-5 . MR 0280994 .
Fefferman, C .; Stein, EM (1972). „H^p mezery několika proměnných“ . Acta Mathematica . 129 : 137–193. doi : 10,1007/BF02392215 . MR 0447953 .
Franks, LE (září 1969). Thomas Kailath (ed.). Teorie signálu . Informační teorie. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0138100772.
Gel'fand, IM ; Shilov, GE (1968). Zobecněné funkce . 2 . Akademický tisk. s. 153–154. ISBN 0-12-279502-4.
Grafakos, Loukas (2004). Klasická a moderní Fourierova analýza . Pearsonovo vzdělávání. s. 253–257. ISBN 0-13-035399-X.
Hardy, GH ; Littlewood, JE ; Pólya, G. (1952). Nerovnosti . Cambridge, Velká Británie: Cambridge University Press. ISBN 0-521-35880-9.
Hilbert, David (1953) [1912]. Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen [ Framework for a General Theory of Linear Integral Equations ] (v němčině). Leipzig & Berlin, DE (1912); New York, NY (1953): BG Teubner (1912); Chelsea Pub. Co. (1953). ISBN 978-3-322-00681-3. OCLC 988251080 . Citováno 2020-12-18 -přes archive.org.CS1 maint: location ( link )
Johansson, Mathias. „Hilbertova transformace, magisterská práce“ (PDF) . Archivováno z originálu (PDF) dne 2012-02-05.; také http://www.fuchs-braun.com/media/d9140c7b3d5004fbffff8007fffffff0.pdf

Kak, Subhash (1970). „Diskrétní Hilbertova transformace“. Proč. IEEE . 58 (4): 585–586. doi : 10.1109/PROC.1970.7696 .
Kak, Subhash (2014). „Teorie čísel Hilbertova transformace“. Zpracování signálu obvodových systémů . 33 (8): 2539–2548. arXiv : 1308,1688 . doi : 10,1007/s00034-014-9759-8 . S2CID 21226699 .
Khvedelidze, BV (2001) [1994], „Hilbertova transformace“ , encyklopedie matematiky , EMS Press
Král, Frederick W. (2009a). Hilbert transformuje . 1 . Cambridge, Velká Británie: Cambridge University Press.
Král, Frederick W. (2009b). Hilbert transformuje . 2 . Cambridge, Velká Británie: Cambridge University Press. p. 453. ISBN 978-0-521-51720-1.
Kress, Rainer (1989). Lineární integrální rovnice . New York, NY: Springer-Verlag. p. 91. ISBN 3-540-50616-0.
Lang, Serge (1985). SL (2, ) ${\ displaystyle \ mathbb {R}}$ . Absolventské texty z matematiky. 105 . New York, NY: Springer-Verlag. ISBN 0-387-96198-4.
Osgood, Brad, The Fourier Transform and its Applications (PDF) , Stanford University , vyvoláno 2021-04-30
Pandey, JN (1996). Hilbertova transformace Schwartzových distribucí a aplikací . Wiley-Interscience. ISBN 0-471-03373-1.
Pichorides, S. (1972). „O nejlepší hodnotě konstant ve větách Riesze, Zygmunda a Kolmogorova“ . Studia Mathematica . 44 (2): 165–179. doi : 10,4064/sm-44-2-165-179 .
Rabiner, Lawrence R .; Zlato, Bernard (1975). „Kapitola 2.27, ekv. 2.195“ . Teorie a aplikace zpracování digitálního signálu . Englewood Cliffs, New Jersey: Prentice-Hall. p. 71 . ISBN 0-13-914101-4.
Riesz, Marcel (1928). „Sur les fonctions conuguées“. Mathematische Zeitschrift (ve francouzštině). 27 (1): 218–244. doi : 10,1007/BF01171098 . S2CID 123261514 .
Rosenblum, Marvin; Rovnyak, James (1997). Hardy třídy a teorie operátorů . Dover. ISBN 0-486-69536-0.
Schwartz, Laurent (1950). Distribuce Théorie des . Paříž, FR: Hermann.
Schreier, P .; Scharf, L. (2010). Statistické zpracování signálu komplexně hodnocených dat: Teorie nevhodných a nekruhových signálů . Cambridge, Velká Británie: Cambridge University Press.
Smith, JO (2007). „Analytické signály a filtry Hilbertovy transformace, v matematice diskrétní Fourierovy transformace (DFT) se zvukovými aplikacemi“ (2. vyd.) . Citováno 2021-04-29 .; také https://www.dsprelated.com/freebooks/mdft/Analytic_Signals_Hilbert_Transform.html

Stein, Elias (1970). Singulární integrály a vlastnosti odlišitelnosti funkcí . Princeton University Press. ISBN 0-691-08079-8.
Stein, Elias ; Weiss, Guido (1971). Úvod do Fourierovy analýzy v euklidovských prostorech . Princeton University Press. ISBN 0-691-08078-X.
Sugiura, Mitsuo (1990). Jednotné reprezentace a harmonická analýza: Úvod . Severní Holandsko Matematická knihovna. 44 (2. vyd.). Elsevier. ISBN 0444885935.
Titchmarsh, E. (1986) [1948]. Úvod do teorie Fourierových integrálů (2. vyd.). Oxford, Velká Británie: Clarendon Press. ISBN 978-0-8284-0324-5.
Tretter, Steven A. (1995). RWLucky (ed.). Návrh komunikačního systému pomocí algoritmů DSP . New York: Springer. ISBN 0306450321.
Zygmund, Antoni (1988) [1968]. Trigonometrická řada (2. vyd.). Cambridge, Velká Británie: Cambridge University Press. ISBN 978-0-521-35885-9.

Další čtení

Benedetto, John J. (1996). Harmonická analýza a její aplikace . Boca Raton, FL: CRC Press. ISBN 0849378796.
Carlson; Crilly & Rutledge (2002). Komunikační systémy (4. vyd.). ISBN 0-07-011127-8.
Zlato, B .; Oppenheim, AV; Rader, CM (1969). „Teorie a implementace diskrétní Hilbertovy transformace“ (PDF) . Proceedings of the 1969 Polytechnic Institute of Brooklyn Symposium . New York . Citováno 2021-04-13 .
Grafakos, Loukas (1994). „Elementární důkaz čtvercové sčítatelnosti diskrétní Hilbertovy transformace“. American Mathematical Monthly . Mathematical Association of America. 101 (5): 456–458. doi : 10,2307/2974910 . JSTOR 2974910 .
Titchmarsh, E. (1926). „Vzájemné vzorce zahrnující řady a integrály“. Mathematische Zeitschrift . 25 (1): 321–347. doi : 10,1007/BF01283842 . S2CID 186237099 .

externí odkazy

Odvození ohraničenosti Hilbertovy transformace
Transformace Mathworld Hilbert - obsahuje tabulku transformací
Weisstein, Eric W. „Titchmarshova věta“ . MathWorld .
„GS256 Přednáška 3: Hilbertova transformace“ (PDF) . Archivováno z originálu (PDF) dne 2012-02-27. úvod do Hilbertovy transformace.

[15] Někteří autoři (např. Bracewell) používajíjako definici dopředné transformacenaše $-H$ . Důsledkem je, že pravý sloupec této tabulky bude negován.

[ex02-16] Hilbertovu transformaci funkcí sin a cos lze definovat tak, že vezmeme hlavní hodnotu integrálu v nekonečnu. Tato definice souhlasí s výsledkem distribuční definice Hilbertovy transformace.

Languages

In other projects