Injektivní funkce - Injective function

V matematice je injektivní funkce (také známá jako injekce nebo funkce one-to-one ) funkce f, která mapuje odlišné prvky na odlišné prvky; to znamená, že f ( x ₁ ) = f ( x ₂ ) znamená x ₁ = x ₂ . Jinými slovy, každý prvek Funkce je codomain je obraz z nanejvýš jeden prvek své domény . Termín one-to-one function nesmí být zaměňován s one-to-one korespondencí, která odkazuje na bijektivní funkce , což jsou funkce takové, že každý prvek v doméně je obrazem přesně jednoho prvku v doméně.

Homomorfizmus mezi algebraické struktury je funkce, která je kompatibilní s operací struktur. Pro všechny běžné algebraické struktury, a zejména pro vektorové prostory , je injektivní homomorfismus také nazýván monomorfismus . V obecnějším kontextu teorie kategorií se však definice monomorfismu liší od definice injektivního homomorfismu. Toto je tedy věta, že jsou ekvivalentní pro algebraické struktury; další podrobnosti viz Homomorphism § Monomorphism .

Funkce, která není injektivní, se někdy nazývá mnoho ku jedné. ${\ displaystyle f}$

Definice

Nechť je funkce, jejíž doménou je množina Funkce je prý injektivní za předpokladu, že pro všechny a v případě, že pak ; to znamená, ekvivalentně, pokud ano${\ displaystyle f}$${\ displaystyle X.}$${\ displaystyle f}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle X,}$${\ Displaystyle f (a) = f (b),}$${\ displaystyle a = b}$${\ Displaystyle f (a) = f (b)}$${\ displaystyle a = b.}$${\ Displaystyle a \ neq b,}$${\ Displaystyle f (a) \ neq f (b).}$

Symbolicky,

$${\ Displaystyle \ forall a, b \ in X, \; \; f (a) = f (b) \ Rightarrow a = b,}$$

$${\ Displaystyle \ forall a, b \ in X, \; \; a \ neq b \ Rightarrow f (a) \ neq f (b).}$$

Příklady

Injektivní funkce. Schematická interpretace v karteziánské rovině , definovaná mapováním, kde doména funkce , rozsah funkce a označuje obraz Každý v mapách přesně jeden jedinečný v Zakroužkované části os představují sady domén a rozsahů - v souladu se standardem diagramy výše.${\ Displaystyle f: X \ až Y,}$${\ displaystyle y = f (x),}$ ${\ displaystyle X =}$${\ displaystyle Y =}$ ${\ displaystyle \ operatorname {im} (f)}$${\ displaystyle f.}$${\ displaystyle x}$${\ displaystyle X}$${\ displaystyle y}$${\ displaystyle Y.}$

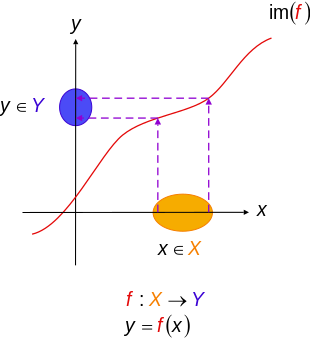
• Pro jakoukoli množinu a jakoukoli podmnožinu je mapa začlenění (která na sebe posílá jakýkoli prvek ) injektivní. Zejména funkce identity je vždy injektivní (a ve skutečnosti bijektivní).${\ displaystyle X}$${\ displaystyle S \ subseteq X,}$ ${\ Displaystyle S \ až X}$${\ displaystyle s \ v S}$ ${\ displaystyle X \ to X}$
• Pokud je doménou funkce prázdná množina , pak je funkcí prázdná funkce , která je injektivní.
• Pokud má doména funkce jeden prvek (to znamená, že je to sada singletonů ), pak je funkce vždy injektivní.
• Funkce definovaná pomocí je injektivní.${\ Displaystyle f: \ mathbb {R} \ to \ mathbb {R}}$${\ displaystyle f (x) = 2x+1}$
• Funkce definované je není injective, protože (například) Nicméně, pokud se nově definována tak, že její oblasti je nezáporná reálná čísla [0, + ∞), potom je injective.${\ Displaystyle g: \ mathbb {R} \ to \ mathbb {R}}$${\ displaystyle g (x) = x^{2}}$${\ Displaystyle g (1) = 1 = g (-1).}$${\ displaystyle g}$${\ displaystyle g}$
• Exponenciální funkce definována injective (ale ne surjektivní, protože skutečné hodnoty se mapuje na číslo negativní).${\ Displaystyle \ exp: \ mathbb {R} \ to \ mathbb {R}}$${\ Displaystyle \ exp (x) = e^{x}}$
• Přirozený logaritmus funkce definována injective.${\ Displaystyle \ ln: (0, \ infty) \ to \ mathbb {R}}$${\ displaystyle x \ mapsto \ ln x}$
• Funkce definovaná pomocí není injektivní, protože např.${\ Displaystyle g: \ mathbb {R} \ to \ mathbb {R}}$${\ Displaystyle g (x) = x^{n} -x}$${\ Displaystyle g (0) = g (1) = 0.}$

Obecněji řečeno, když a jsou obě skutečnou přímkou, pak injektivní funkcí je ta, jejíž graf není nikdy protnut žádnou vodorovnou čarou více než jednou. Tento princip se označuje jako test horizontální čáry . ${\ displaystyle X}$${\ displaystyle Y}$ ${\ displaystyle \ mathbb {R},}$${\ Displaystyle f: \ mathbb {R} \ to \ mathbb {R}}$

Není to injektivní funkce. Tady a jsou podmnožiny a jsou podmnožiny : na obou regionech, kde tato funkce není injective protože více než jedna doména prvek lze mapovat do jednoho rozsah prvku. To znamená, že je možné, že více než jeden v mapovat na stejné inu${\ displaystyle X_ {1}}$${\ displaystyle X_ {2}}$${\ displaystyle X, Y_ {1}}$${\ displaystyle Y_ {2}}$${\ displaystyle Y}$ ${\ displaystyle x}$${\ displaystyle X}$ ${\ displaystyle y}$${\ displaystyle Y.}$

Injektivní funkce. Předchozí funkci lze zredukovat na jednu nebo více injektivních funkcí (řekněme) a zobrazit pomocí plných křivek (dlouhé pomlčky částí počáteční křivky již nejsou mapovány). Všimněte si, jak se pravidlo nezměnilo - pouze doména a rozsah. a jsou podmnožinami a jsou podmnožinami : pro dvě oblasti, kde lze počáteční funkci učinit injektivní, takže jeden prvek domény lze mapovat na prvek jednoho rozsahu. To znamená, že pouze jeden v mapách k jednomu v${\ Displaystyle f: X \ až Y}$${\ displaystyle f: X_ {1} \ to Y_ {1}}$${\ displaystyle f: X_ {2} \ to Y_ {2},}$${\ displaystyle f}$${\ displaystyle X_ {1}}$${\ displaystyle X_ {2}}$${\ displaystyle X, Y_ {1}}$${\ displaystyle Y_ {2}}$${\ displaystyle Y}$${\ displaystyle x}$${\ displaystyle X}$${\ displaystyle y}$${\ displaystyle Y.}$

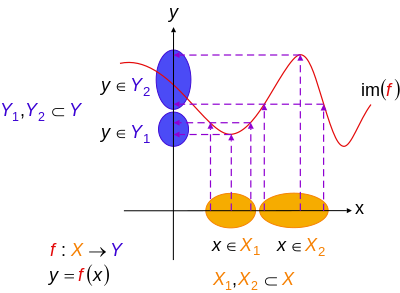
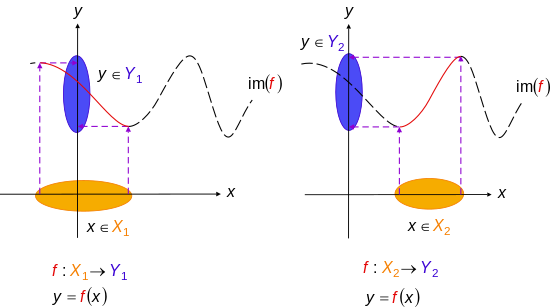
Injekce lze vrátit zpět

Funkce s levými inverzemi jsou vždy injekce. To je dáno, pokud existuje funkce taková, že pro každého${\ Displaystyle f: X \ až Y,}$${\ displaystyle g: Y \ to X}$${\ displaystyle x \ v X,}$

${\ Displaystyle g (f (x)) = x}$( lze vrátit zpět ), pak je injektivní. V tomto případě, se nazývá zatažení z naopak, se nazývá část z${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle f.}$${\ displaystyle f}$${\ Displaystyle g.}$

Naopak každá injekce s prázdnou doménou má levou inverzi, kterou lze definovat fixací prvku v doméně tak, aby se rovnal jedinečnému předobrazu pod, pokud existuje, a jinak. ${\ displaystyle f}$${\ displaystyle g,}$${\ displaystyle a}$${\ displaystyle f}$${\ displaystyle g (x)}$${\ displaystyle x}$${\ displaystyle f}$${\ displaystyle g (x) = 1}$

Levá inverzní není nutně inverzní z , protože kompozice v jiném pořadí, může lišit od identity na Jinými slovy, prosté zobrazení může být „obrácené“ od levé inverzní, ale nemusí být nutně invertovat , což vyžaduje, aby se funkce je bijektivní. ${\ displaystyle g}$${\ displaystyle f,}$${\ Displaystyle f \ circ g,}$${\ displaystyle Y.}$

Injekce mohou být invertibilní

Ve skutečnosti k přeměně injektivní funkce na bijektivní (potažmo invertovatelnou) funkci stačí nahradit její doménu jejím skutečným rozsahem. To znamená, nechat tak, že pro všechny ; pak je bijektivní. Ve skutečnosti může být factored jak , kde je funkce zahrnutí od do${\ Displaystyle f: X \ až Y}$${\ displaystyle Y}$${\ Displaystyle J = f (X).}$${\ displaystyle g: X \ to J}$${\ Displaystyle g (x) = f (x)}$${\ displaystyle x \ v X}$${\ displaystyle g}$${\ displaystyle f}$${\ displaystyle \ operatorname {In} _ {J, Y} \ circ g,}$${\ displaystyle \ operatorname {In} _ {J, Y}}$${\ displaystyle J}$${\ displaystyle Y.}$

Obecněji se injektivní dílčí funkce nazývají částečné bijekce .

Další vlastnosti

• Pokud a jsou oba injektivní, pak je injektivní.${\ displaystyle f}$${\ displaystyle g}$${\ Displaystyle f \ circ g}$

Složení dvou injektivních funkcí je injektivní.

• Pokud je injektivní, pak je injektivní (ale nemusí být).${\ Displaystyle g \ circ f}$${\ displaystyle f}$${\ displaystyle g}$
• ${\ Displaystyle f: X \ až Y}$je injektivní právě tehdy, když je dána nějaká funkce kdykoli potom Jinými slovy, injektivní funkce jsou přesně monomorfismy v kategorii Sada množin.${\ displaystyle g,}$ ${\ Displaystyle h: W \ až X}$${\ Displaystyle f \ circ g = f \ circ h,}$${\ Displaystyle g = h.}$
• Pokud je injective a je podmnožina z pak tedy může získat z jeho obrazu${\ Displaystyle f: X \ až Y}$${\ displaystyle A}$${\ displaystyle X,}$${\ Displaystyle f^{-1} (f (A)) = A.}$${\ displaystyle A}$ ${\ Displaystyle f (A).}$
• If je injektivní a a jsou obě podmnožinami tehdy${\ Displaystyle f: X \ až Y}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle X,}$${\ Displaystyle f (A \ cap B) = f (A) \ cap f (B).}$
• Každá funkce lze rozložit na vhodnou injekci a surjekce Tento rozklad je unikátní do izomorfismu , a může být myšlenka jako funkce zahrnutí rozsahu z jako podmnožina codomain z${\ Displaystyle h: W \ až Y}$${\ Displaystyle h = f \ circ g}$${\ displaystyle f}$${\ Displaystyle g.}$${\ displaystyle f}$${\ displaystyle h (W)}$${\ displaystyle h}$${\ displaystyle Y}$${\ Displaystyle h.}$
• Pokud je to injektivní funkce, pak má alespoň tolik prvků jako ve smyslu základních čísel . Zejména, pokud kromě toho, že je injekce od až poté , a mají stejné kardinální číslo. (Toto je známé jako Cantor – Bernstein – Schroederova věta .)${\ Displaystyle f: X \ až Y}$${\ displaystyle Y}$${\ displaystyle X,}$${\ displaystyle Y}$${\ displaystyle X,}$${\ displaystyle X}$${\ displaystyle Y}$
• Pokud jsou oba a jsou konečné se stejným počtem prvků, pak je injektivní, pokud a pouze pokud je surjektivní (v takovém případě je bijektivní).${\ displaystyle X}$${\ displaystyle Y}$${\ Displaystyle f: X \ až Y}$${\ displaystyle f}$${\ displaystyle f}$
• Injektivní funkce, která je homomorfismem mezi dvěma algebraickými strukturami, je vložení .
• Na rozdíl od surjectivity, což je vztah mezi grafem funkce a její doménou, injektivita je vlastností grafu samotné funkce; to znamená, že zda je funkce injektivní, může být rozhodnuto pouze s ohledem na graf (a ne na doménu)${\ displaystyle f}$${\ displaystyle f.}$

Dokázat, že funkce jsou injektivní

Důkaz, že funkce je injektivní, závisí na tom, jak je funkce prezentována a jaké vlastnosti funkce obsahuje. Pro funkce, které jsou dány nějakým vzorcem, existuje základní myšlenka. Používáme definici injektivity, totiž že pokud ano${\ displaystyle f}$${\ Displaystyle f (x) = f (y),}$${\ Displaystyle x = y.}$

Zde je příklad:

$${\ displaystyle f (x) = 2x+3}$$

Důkaz: Předpokládejme, že to znamená, což znamená, proto to vyplývá z definice, která je injektivní. ${\ Displaystyle f: X \ až Y.}$${\ Displaystyle f (x) = f (y).}$${\ Displaystyle 2x+3 = 2y+3}$${\ displaystyle 2x = 2r,}$${\ Displaystyle x = y.}$${\ displaystyle f}$

Existuje několik dalších způsobů, jak prokázat, že funkce je injektivní. Například v počtu if je diferencovatelná funkce definovaná v nějakém intervalu, pak stačí ukázat, že derivace je v tomto intervalu vždy kladná nebo vždy záporná. Pokud je v lineární algebře lineární transformace, stačí ukázat, že jádro obsahuje pouze nulový vektor. Pokud jde o funkci s konečnou doménou, stačí se podívat do seznamu obrázků každého prvku domény a zkontrolovat, zda se v seznamu dvakrát neobjeví žádný obrázek. ${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f}$

Grafický přístup pro funkci reálné hodnoty reálné hodnoty je test horizontální čáry . Pokud každá vodorovná čára protíná křivku nejvýše v jednom bodě, pak je injektivní nebo individuální. ${\ displaystyle f}$${\ displaystyle x}$${\ displaystyle f (x)}$${\ displaystyle f}$

Viz také

• Bijekce, injekce a surjekce  - Vlastnosti matematických funkcí
• Injektivní metrický prostor  - Typ metrického prostoru
• Monotónní funkce
• Univalentní funkce

Poznámky

Reference

• Bartle, Robert G. (1976), The Elements of Real Analysis (2. vyd.), New York: John Wiley & Sons , ISBN 978-0-471-05464-1, str. 17 a násl .
• Halmos, Paul R. (1974), Naivní teorie množin , New York: Springer, ISBN 978-0-387-90092-6, str. 38 a násl .

externí odkazy

• Nejčasnější použití některých slov z matematiky: vstup na téma Injekce, Surjekce a Bijekce má historii injekce a související termíny.
• Khan Academy-Surjective (onto) and Injective (one-to-one) functions: Introduction to surjective and injective functions