Nejmenší čtverce - Least squares

Výsledek přizpůsobení sady datových bodů kvadratické funkci

Kónický tvar množiny bodů pomocí aproximace nejmenších čtverců

Metoda nejmenších čtverců je standardním přístupem v regresní analýze k aproximaci řešení přeurčených systémů (sady rovnic, ve kterých je více rovnic než neznámých) minimalizací součtu čtverců zbytků vytvořených ve výsledcích každé jednotlivé rovnice .

Nejdůležitější aplikace je v přizpůsobení dat . Nejlepší shoda ve smyslu nejmenších čtverců minimalizuje součet čtvercových zbytků (zbytková bytost: rozdíl mezi pozorovanou hodnotou a přizpůsobenou hodnotou poskytnutou modelem). Když má problém značnou nejistotu v nezávislé proměnné ( proměnné x ), pak mají jednoduché regresní metody a metody nejmenších čtverců problémy; v takových případech lze místo metod pro nejmenší čtverce zvážit metodiku požadovanou pro přizpůsobení modelů chyb v proměnných .

Problémy s nejmenšími čtverci spadají do dvou kategorií: lineární nebo obyčejné nejmenší čtverce a nelineární nejmenší čtverce , v závislosti na tom, zda jsou zbytky lineární ve všech neznámých. Problém lineárních nejmenších čtverců se vyskytuje ve statistické regresní analýze ; má řešení v uzavřené formě . Nelineární problém je obvykle vyřešen iteračním upřesněním; při každé iteraci je systém aproximován lineární, a proto je základní výpočet v obou případech podobný.

Polynomické nejmenší čtverce popisují rozptyl v predikci závislé proměnné jako funkci nezávislé proměnné a odchylky od přizpůsobené křivky.

Když pozorování pocházejí z exponenciální rodiny s identitou, protože jsou splněny její přirozené dostatečné statistiky a mírné podmínky (např. Pro normální, exponenciální, Poissonovo a binomické rozdělení), standardizované odhady nejmenších čtverců a odhady maximální pravděpodobnosti jsou totožné. Metodu nejmenších čtverců lze také odvodit jako metodu odhadu momentů .

Následující diskuse je většinou prezentována z hlediska lineárních funkcí, ale použití nejmenších čtverců je platné a praktické pro obecnější rodiny funkcí. Také iterativním použitím lokální kvadratické aproximace na pravděpodobnost (prostřednictvím Fisherových informací ) lze použít metodu nejmenších čtverců, aby odpovídala zobecněnému lineárnímu modelu .

Metoda nejmenších čtverců byla oficiálně objevena a publikována Adrienem-Marie Legendrem (1805), ačkoli je obvykle také spoluvěřína Carlu Friedrichovi Gaussovi (1795), který k metodě přispěl významným teoretickým pokrokem a možná ji dříve použil ve svém práce.

Dějiny

Založení

Metoda nejmenších čtverců vyrostla z oblastí astronomie a geodézie , protože vědci a matematici se snažili poskytnout řešení problémů spojených s navigací po pozemských oceánech během Věku průzkumu . Přesný popis chování nebeských těles byl klíčem k tomu, aby mohly lodě plout na otevřeném moři, kde se námořníci již nemohli spoléhat na navigaci na pozorování pevniny.

Tato metoda byla vyvrcholením několika pokroků, ke kterým došlo v průběhu osmnáctého století:

Kombinace různých pozorování jako nejlepší odhad skutečné hodnoty; chyby se s agregací spíše snižují než zvyšují, možná poprvé vyjádřil Roger Cotes v roce 1722.
Kombinace různých pozorování pořízených za stejných podmínek, která je v rozporu s tím, že se člověk prostě snaží pozorovat a přesně zaznamenat jediné pozorování. Tento přístup byl znám jako metoda průměrů. Tento přístup používal zejména Tobias Mayer při studiu měsíčních knihoven v roce 1750 a Pierre-Simon Laplace ve své práci při vysvětlování rozdílů v pohybu Jupitera a Saturnu v roce 1788.
Kombinace různých pozorování pořízených za různých podmínek. Metoda začala být známá jako metoda nejmenší absolutní odchylky. To bylo zejména provedeno Rogerem Josephem Boscovichem v jeho práci na tvaru země v roce 1757 a Pierre-Simonem Laplaceem pro stejný problém v roce 1799.
Vývoj kritéria, které lze vyhodnotit a určit, kdy bylo dosaženo řešení s minimální chybou. Laplace se pokusil určit matematickou formu hustoty pravděpodobnosti chyb a definovat metodu odhadu, která minimalizuje chybu odhadu. Za tímto účelem Laplace použil k modelování rozdělení chyb symetrické oboustranné exponenciální rozdělení, které nyní nazýváme Laplaceova distribuce, a jako chybu odhadu použil součet absolutní odchylky. Cítil, že to jsou nejjednodušší předpoklady, které mohl učinit, a doufal, že získá aritmetický průměr jako nejlepší odhad. Místo toho byl jeho odhad zadní medián.

Metoda

Carl Friedrich Gauss

První jasná a stručná expozice metody nejmenších čtverců byla publikována Legendrem v roce 1805. Tato technika je popsána jako algebraický postup pro přizpůsobení lineárních rovnic k datům a Legendre demonstruje novou metodu analýzou stejných dat jako Laplace pro tvar Země. Do deseti let po vydání Legendra byla metoda nejmenších čtverců přijata jako standardní nástroj v astronomii a geodézii ve Francii, Itálii a Prusku, což představuje mimořádně rychlé přijetí vědecké techniky.

V roce 1809 Carl Friedrich Gauss publikoval svou metodu výpočtu oběžných drah nebeských těles. V této práci prohlašoval, že vlastní metodu nejmenších čtverců od roku 1795. To přirozeně vedlo k prioritnímu sporu s Legendrem. Nicméně, ke cti Gaussovi, šel za Legendre a podařilo se mu propojit metodu nejmenších čtverců s principy pravděpodobnosti a s normálním rozdělením . Podařilo se mu dokončit Laplaceův program určující matematickou formu hustoty pravděpodobnosti pro pozorování v závislosti na konečném počtu neznámých parametrů a definovat metodu odhadu, která minimalizuje chybu odhadu. Gauss ukázal, že aritmetický průměr je skutečně nejlepším odhadem parametru umístění změnou hustoty pravděpodobnosti i metody odhadu. Poté problém otočil otázkou, jakou formu by měla mít hustota a jakou metodu odhadu použít k získání aritmetického průměru jako odhadu parametru umístění. Při tomto pokusu vynalezl normální rozdělení.

Časná demonstrace síly Gaussovy metody přišla, když byla použita k předpovědi budoucího umístění nově objeveného asteroidu Ceres . 1. ledna 1801 objevil italský astronom Giuseppe Piazzi Ceres a byl schopen sledovat jeho cestu po dobu 40 dnů, než se ztratil v záři slunce. Na základě těchto údajů si astronomové přáli určit polohu Ceres poté, co se vynořilo zpoza Slunce, aniž by vyřešily Keplerovy komplikované nelineární rovnice planetárního pohybu. Jediné předpovědi, které úspěšně umožnily maďarskému astronomovi Franzi Xaverovi von Zachovi přemístit Ceres, byly předpovědi provedené 24letým Gaussem pomocí analýzy nejmenších čtverců.

V roce 1810, po přečtení Gaussova díla, ho Laplace po prokázání centrální limitní věty použil k poskytnutí velkého odůvodnění vzorku pro metodu nejmenších čtverců a normální distribuce. V roce 1822 byl Gauss schopen prohlásit, že přístup nejmenších čtverců k regresní analýze je optimální v tom smyslu, že v lineárním modelu, kde chyby mají průměr nula, jsou nekorelované a mají stejné odchylky, nejlepší lineární nezaujatý odhad koeficienty jsou odhad nejmenších čtverců. Tento výsledek je známý jako Gaussova -Markovova věta .

Myšlenku analýzy nejmenších čtverců také nezávisle formuloval Američan Robert Adrain v roce 1808. V příštích dvou stoletích našli pracovníci v teorii chyb a ve statistikách mnoho různých způsobů implementace nejmenších čtverců.

Problémové prohlášení

Cílem je upravit parametry modelové funkce tak, aby co nejlépe odpovídaly datové sadě. Jednoduchý datový soubor se skládá z n bodů (datových párů) , i = 1,…, n , kde je nezávislou proměnnou a je závislou proměnnou, jejíž hodnotu zjistíme pozorováním. Funkce modelu má tvar , kde jsou ve vektoru drženy m nastavitelné parametry . Cílem je najít hodnoty parametrů pro model, který „nejlépe“ odpovídá datům. Přizpůsobení modelu datovému bodu se měří jeho zbytkem , definovaným jako rozdíl mezi pozorovanou hodnotou závislé proměnné a hodnotou predikovanou modelem: ${\ displaystyle (x_ {i}, y_ {i}) \!}$ ${\ displaystyle x_ {i} \!}$ ${\ displaystyle y_ {i} \!}$ ${\ displaystyle f (x, {\ boldsymbol {\ beta}})}$ ${\ displaystyle {\ boldsymbol {\ beta}}}$

{\ displaystyle r_ {i} = y_ {i} -f (x_ {i}, {\ boldsymbol {\ beta}}).}

Zbytky jsou vyneseny proti odpovídajícím hodnotám. Náhodné výkyvy kolem naznačují, že lineární model je vhodný.

{\ displaystyle x}

{\ displaystyle r_ {i} = 0}

Metoda nejmenších čtverců najde optimální hodnoty parametru minimalizací součet kvadratických zbytků , : ${\ displaystyle S}$

{\ Displaystyle S = \ sum _ {i = 1}^{n} r_ {i}^{2}.}

Příkladem modelu ve dvou rozměrech je přímka. Označením zachycení y jako a sklonu as je funkce modelu dána vztahem . Plně zpracovaný příklad tohoto modelu najdete v lineárních nejmenších čtvercích . ${\ displaystyle \ beta _ {0}}$ ${\ displaystyle \ beta _ {1}}$ ${\ Displaystyle f (x, {\ boldsymbol {\ beta}}) = \ beta _ {0}+\ beta _ {1} x}$

Datový bod může sestávat z více než jedné nezávislé proměnné. Například při montáži roviny do sady měření výšky je rovina funkcí dvou nezávislých proměnných , řekněme x a z . V nejobecnějším případě může být v každém datovém bodě jedna nebo více nezávislých proměnných a jedna nebo více závislých proměnných.

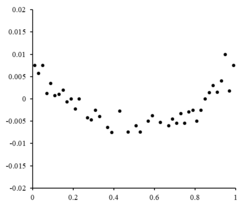
Vpravo je zbytkový graf ilustrující náhodné výkyvy kolem , což naznačuje, že je vhodný lineární model . je nezávislá, náhodná proměnná. ${\ displaystyle r_ {i} = 0}$ ${\ displaystyle (Y_ {i} = \ alpha +\ beta x_ {i} +U_ {i})}$ ${\ displaystyle U_ {i}}$

Zbytky jsou vyneseny proti odpovídajícím hodnotám. Parabolický tvar fluktuací naznačuje, že parabolický model je vhodný.

{\ displaystyle x}

{\ displaystyle r_ {i} = 0}

Pokud by zbytkové body měly nějaký tvar a nebyly náhodně kolísavé, nebyl by lineární model vhodný. Pokud by například reziduální graf měl parabolický tvar, jak je vidět napravo, pro data by byl vhodný parabolický model . Zbytky pro parabolický model lze vypočítat pomocí . ${\ Displaystyle (Y_ {i} = \ alpha+\ beta x_ {i}+\ gamma x_ {i}^{2}+U_ {i})}$ ${\ Displaystyle r_ {i} = y_ {i}-{\ hat {\ alpha}}-{\ hat {\ beta}} x_ {i}-{\ widehat {\ gamma}} x_ {i}^{2 }}$

Omezení

Tato regresní formulace bere v úvahu pouze pozorovací chyby v závislé proměnné (ale alternativní celková regrese nejmenších čtverců může vysvětlovat chyby v obou proměnných). Existují dva poměrně odlišné kontexty s různými důsledky:

Regrese pro predikci. Zde je model vybaven tak, aby poskytoval predikční pravidlo pro aplikaci v podobné situaci, na kterou se vztahují data použitá pro přizpůsobení. Zde by závislé proměnné odpovídající takové budoucí aplikaci podléhaly stejným typům chyby pozorování, jaké jsou v datech použitých pro přizpůsobení. Je proto logicky konzistentní pro takové údaje použít pravidlo predikce nejmenších čtverců.
Regrese za přizpůsobení „skutečného vztahu“. Ve standardní regresní analýze, která vede k přizpůsobení nejmenším čtvercům, existuje implicitní předpoklad, že chyby v nezávislé proměnné jsou nulové nebo přísně kontrolované tak, aby byly zanedbatelné. Pokud jsou chyby v nezávislé proměnné nezanedbatelné, lze použít modely chyby měření ; takové metody mohou vést k odhadům parametrů , testování hypotéz a intervalům spolehlivosti, které berou v úvahu přítomnost chyb pozorování v nezávislých proměnných. Alternativní přístup je přizpůsobit model celkově nejmenšími čtverci ; na to lze pohlížet jako na pragmatický přístup k vyvažování účinků různých zdrojů chyb při formulování objektivní funkce pro použití při sestavování modelu.

Řešení problému nejmenších čtverců

Minimální součtu čtverců se nachází nastavením gradientu na nulu. Protože model obsahuje m parametrů, existuje m gradientních rovnic:

{\ Displaystyle {\ frac {\ částečný S} {\ částečný \ beta _ {j}}} = 2 \ součet _ {i} r_ {i} {\ frac {\ částečný r_ {i}} {\ částečný \ beta _ {j}}} = 0, \ j = 1, \ ldots, m,}

a od té doby přechází rovnice ${\ displaystyle r_ {i} = y_ {i} -f (x_ {i}, {\ boldsymbol {\ beta}})}}$

{\ Displaystyle -2 \ sum _ {i} r_ {i} {\ frac {\ částečné f (x_ {i}, {\ boldsymbol {\ beta}})} {\ částečné \ beta _ {j}}} = 0, \ j = 1, \ ldots, m.}

Gradientní rovnice platí pro všechny úlohy nejmenších čtverců. Každý konkrétní problém vyžaduje konkrétní výrazy pro model a jeho dílčí derivace.

Lineární nejmenší čtverce

Regresní model je lineární, pokud model obsahuje lineární kombinaci parametrů, tj.

{\ Displaystyle f (x, {\ boldsymbol {\ beta}}) = \ sum _ {j = 1}^{m} \ beta _ {j} \ phi _ {j} (x),}

kde funkce je funkcí . ${\ displaystyle \ phi _ {j}}$ ${\ displaystyle x}$

Nechání a vložení nezávislých a závislých proměnných do matic a respektive můžeme nejmenší čtverce vypočítat následujícím způsobem. Všimněte si, že toto je sada všech dat. ${\ Displaystyle X_ {ij} = \ phi _ {j} (x_ {i})}$ ${\ displaystyle X}$ ${\ displaystyle Y}$ ${\ displaystyle D}$

{\ Displaystyle L (D, {\ boldsymbol {\ beta}}) = \ left \ | YX {\ boldsymbol {\ beta}} \ right \ |^{2} = (YX {\ boldsymbol {\ beta}}) ^{\ mathsf {T}} (YX {\ boldsymbol {\ beta}}) = Y^{\ mathsf {T}} YY^{\ mathsf {T}} X {\ boldsymbol {\ beta}}-{\ boldsymbol {\ beta}}^{\ mathsf {T}} X^{\ mathsf {T}} Y+{\ boldsymbol {\ beta}}^{\ mathsf {T}} X^{\ mathsf {T}} X {\ boldsymbol {\ beta}}}

Nalezení minima lze dosáhnout nastavením gradientu ztráty na nulu a řešením pro ${\ displaystyle {\ vec {\ beta}}}$

{\ Displaystyle {\ frac {\ částečný L (D, {\ boldsymbol {\ beta}})} {\ částečný {\ boldsymbol {\ beta}}}} = {\ frac {\ částečný \ vlevo (Y^{\ mathsf {T}} YY^{\ mathsf {T}} X {\ boldsymbol {\ beta}}-{\ boldsymbol {\ beta}}^{\ mathsf {T}} X^{\ mathsf {T}} Y+ {\ boldsymbol {\ beta}}^{\ mathsf {T}} X^{\ mathsf {T}} X {\ boldsymbol {\ beta}} \ right)} {\ partial {\ boldsymbol {\ beta}}} } =-2X^{\ mathsf {T}} Y+2X^{\ mathsf {T}} X {\ boldsymbol {\ beta}}}

Nakonec nastavením gradientu ztráty na nulu a řešením pro dostaneme: ${\ displaystyle {\ boldsymbol {\ beta}}}$

{\ Displaystyle -2X^{\ mathsf {T}} Y+2X^{\ mathsf {T}} X {\ boldsymbol {\ beta}} = 0 \ Rightarrow X^{\ mathsf {T}} Y = X^ {\ mathsf {T}} X {\ boldsymbol {\ beta}}}

{\ Displaystyle {\ boldsymbol {\ hat {\ beta}}} = \ left (X^{\ mathsf {T}} X \ right)^{-1} X^{\ mathsf {T}} Y}

Nelineární nejmenší čtverce

V některých případech existuje řešení nelineární úlohy nejmenších čtverců v uzavřené formě -ale obecně neexistuje. V případě, že neexistuje řešení uzavřené formy, jsou k nalezení hodnoty parametrů, které minimalizují cíl, použity numerické algoritmy . Většina algoritmů zahrnuje výběr počátečních hodnot pro parametry. Poté jsou parametry upřesněny iterativně, to znamená, že hodnoty jsou získány postupnou aproximací: ${\ displaystyle \ beta}$

{\ displaystyle {\ beta _ {j}}^{k+1} = {\ beta _ {j}}^{k}+\ Delta \ beta _ {j},}

kde horní index k je iterační číslo a vektor přírůstků se nazývá vektor posunu. V některých běžně používaných algoritmech může být model při každé iteraci linearizován aproximací k rozšíření řady Taylor prvního řádu o : ${\ displaystyle \ Delta \ beta _ {j}}$ ${\ displaystyle {\ boldsymbol {\ beta}}^{k}}$

{\ displaystyle {\ begin {aligned} f (x_ {i}, {\ boldsymbol {\ beta}}) & = f^{k} (x_ {i}, {\ boldsymbol {\ beta}})+\ sum _ {j} {\ frac {\ částečné f (x_ {i}, {\ boldsymbol {\ beta}})} {\ částečné \ beta _ {j}}} \ vlevo (\ beta _ {j}-{\ beta _ {j}}^{k} \ right) \\ & = f^{k} (x_ {i}, {\ boldsymbol {\ beta}})+\ sum _ {j} J_ {ij} \, \ Delta \ beta _ {j}. \ End {aligned}}}

Jacobian J je funkcí konstanty, nezávislé proměnné a parametrů, takže se mění od jednoho opakování k dalšímu. Zbytky jsou dány

{\ Displaystyle r_ {i} = y_ {i} -f^{k} (x_ {i}, {\ boldsymbol {\ beta}})-\ sum _ {k = 1}^{m} J_ {ik} \, \ Delta \ beta _ {k} = \ Delta y_ {i}-\ sum _ {j = 1}^{m} J_ {ij} \, \ Delta \ beta _ {j}.}

Aby se minimalizoval součet druhých mocnin , je rovnice přechodu nastavena na nulu a řešena pro : ${\ displaystyle r_ {i}}$ ${\ displaystyle \ Delta \ beta _ {j}}$

{\ Displaystyle -2 \ sum _ {i = 1}^{n} J_ {ij} \ left (\ Delta y_ {i} -\ sum _ {k = 1}^{m} J_ {ik} \, \ Delta \ beta _ {k} \ vpravo) = 0,}

které se při přeskupení stávají m simultánními lineárními rovnicemi, normální rovnice :

{\ Displaystyle \ sum _ {i = 1}^{n} \ sum _ {k = 1}^{m} J_ {ij} J_ {ik} \, \ Delta \ beta _ {k} = \ sum _ { i = 1}^{n} J_ {ij} \, \ Delta y_ {i} \ qquad (j = 1, \ ldots, m).}

Normální rovnice jsou zapsány v maticovém zápisu jako

{\ Displaystyle \ left (\ mathbf {J} ^{\ mathsf {T}} \ mathbf {J} \ right) \ Delta {\ boldsymbol {\ beta}} = \ mathbf {J} ^{\ mathsf {T} } \ Delta \ mathbf {y}.}

Toto jsou definující rovnice Gaussova -Newtonova algoritmu .

Rozdíly mezi lineárními a nelineárními nejmenšími čtverci

Funkce modelu, f , v LLSQ (lineární nejmenší čtverce) je lineární kombinací parametrů formuláře Model může představovat přímku, parabolu nebo jakoukoli jinou lineární kombinaci funkcí. V NLLSQ (nelineární nejmenší čtverce) se parametry zobrazují jako funkce, například a tak dále. Pokud jsou deriváty buď konstantní, nebo závisí pouze na hodnotách nezávislé proměnné, je model v parametrech lineární. Jinak je model nelineární. ${\ displaystyle f = X_ {i1} \ beta _ {1}+X_ {i2} \ beta _ {2}+\ cdots}$ ${\ displaystyle \ beta ^{2}, e ^{\ beta x}}$ ${\ Displaystyle \ částečná f/\ částečná \ beta _ {j}}$
Potřebujete počáteční hodnoty parametrů, abyste našli řešení problému NLLSQ; LLSQ je nevyžaduje.
Algoritmy řešení pro NLLSQ často vyžadují, aby byl Jacobian vypočítán podobně jako LLSQ. Analytické výrazy pro parciální derivace mohou být komplikované. Pokud není možné získat analytické výrazy, musí být dílčí derivace vypočítány numerickou aproximací nebo musí být proveden odhad jakobijského, často prostřednictvím konečných rozdílů .
Nekonvergence (selhání algoritmu najít minimum) je v NLLSQ běžným jevem.
LLSQ je globálně konkávní, takže nekonvergence není problém.
Řešení NLLSQ je obvykle iterační proces, který musí být ukončen, když je splněno konvergenční kritérium. Řešení LLSQ lze vypočítat pomocí přímých metod, i když problémy s velkým počtem parametrů jsou obvykle řešeny iterativními metodami, jako je například metoda Gauss -Seidel .
V LLSQ je řešení jedinečné, ale v NLLSQ může existovat více minim v součtu čtverců.
Za podmínky, že chyby nejsou korelovány s prediktorovými proměnnými, LLSQ poskytuje nestranné odhady, ale i za této podmínky jsou odhady NLLSQ obecně zkreslené.

Tyto rozdíly je třeba vzít v úvahu vždy, když se hledá řešení nelineárního problému nejmenších čtverců.

Příklad

Zvažte jednoduchý příklad z fyziky. Pružina by se měla řídit Hookeovým zákonem, který říká, že prodloužení pružiny $y$ je úměrné síle F , která na ni působí.

{\ Displaystyle y = f (F, k) = kF \!}

představuje model, kde F je nezávislá proměnná. Abychom odhadli silovou konstantu , k , provedeme sérii n měření s různými silami k vytvoření sady dat , kde y _i je změřené prodloužení pružiny. Každé experimentální pozorování bude obsahovat nějakou chybu, a proto můžeme pro naše pozorování určit empirický model, ${\ Displaystyle (F_ {i}, y_ {i}), \ i = 1, \ tečky, n \!}$ ${\ displaystyle \ varepsilon}$

{\ Displaystyle y_ {i} = kF_ {i}+\ varepsilon _ {i}. \,}

K odhadu neznámého parametru k můžeme použít mnoho metod . Protože n rovnic v m proměnných v našich datech obsahuje předurčený systém s jednou neznámou a n rovnicemi, odhadujeme k pomocí nejmenších čtverců. Součet čtverců, které je třeba minimalizovat, je

{\ Displaystyle S = \ sum _ {i = 1}^{n} (y_ {i} -kF_ {i})^{2}.}

Odhad nejmenších čtverců silové konstanty, k , je dán vztahem

{\ displaystyle {\ hat {k}} = {\ frac {\ sum _ {i} F_ {i} y_ {i}} {\ sum _ {i} F_ {i}^{2}}}.}

Předpokládáme, že působící síla způsobí roztažení pružiny. Poté, co jsme odvodili silovou konstantu pomocí přizpůsobení nejmenších čtverců, předpovídáme rozšíření z Hookeova zákona.

Kvantifikace nejistoty

Při výpočtu nejmenších čtverců s jednotkovými hmotnostmi nebo v lineární regresi se rozptyl j -tého parametru, označeného , obvykle odhaduje pomocí ${\ displaystyle \ operatorname {var} ({\ hat {\ beta}} _ {j})}$

{\ displaystyle \ operatorname {var} ({\ hat {\ beta}} _ {j}) = \ sigma^{2} \ left (\ left [X^{\ mathsf {T}} X \ right]^{ -1} \ vpravo) _ {jj} \ cca {\ hat {\ sigma}}^{2} C_ {jj},}

{\ Displaystyle {\ hat {\ sigma}}^{2} \ cca {\ frac {S} {nm}}}

{\ Displaystyle C = \ left (X^{\ mathsf {T}} X \ right)^{-1},}

kde platí variance odchylky σ ² je nahrazen odhadem, na sníženou chí-kvadrát statistiky , vztaženo na minimalizované hodnoty zbytkového součtu čtverců (objektivní funkce), S . Jmenovatelem n - m jsou statistické stupně volnosti ; zevšeobecnění viz efektivní stupně volnosti . C je kovarianční matice .

Statistické testování

Je -li známé rozdělení pravděpodobnosti parametrů nebo je provedena asymptotická aproximace, lze najít meze spolehlivosti . Podobně lze statistické testy reziduí provádět, pokud je rozdělení pravděpodobnosti reziduí známé nebo předpokládané. Pokud je rozdělení pravděpodobnosti experimentálních chyb známé nebo předpokládané, můžeme odvodit rozdělení pravděpodobnosti jakékoli lineární kombinace závislých proměnných. Odvození je snadné za předpokladu, že chyby sledují normální rozdělení, z čehož vyplývá, že odhady parametrů a zbytky budou také normálně distribuovány za podmínky hodnot nezávislých proměnných.

Je nutné učinit předpoklady o povaze experimentálních chyb, abychom výsledky statisticky testovali. Běžným předpokladem je, že chyby patří do normální distribuce. Centrální limitní věta podporuje myšlenku, že se jedná o dobré přiblížení v mnoha případech.

Gauss-Markov teorém . V lineárním modelu, ve kterém mají chyby očekávání nulové podmíněné nezávislými proměnnými, jsou nekorelované a mají stejné odchylky , je nejlepším lineárním nezaujatým odhadem jakékoli lineární kombinace pozorování jeho odhad nejmenších čtverců. „Nejlepší“ znamená, že odhady nejmenších čtverců parametrů mají minimální rozptyl. Předpoklad stejné odchylky platí, když všechny chyby patří do stejné distribuce.
Pokud chyby patří k normálnímu rozdělení, odhady nejmenších čtverců jsou také odhady maximální pravděpodobnosti v lineárním modelu.

Předpokládejme však, že chyby nejsou běžně distribuovány. V takovém případě centrální limitní věta často nicméně znamená, že odhady parametrů budou přibližně normálně distribuovány, pokud je vzorek přiměřeně velký. Z tohoto důvodu, vzhledem k důležité vlastnosti, že průměr chyby je nezávislý na nezávislých proměnných, není rozdělení chybového výrazu důležitou otázkou v regresní analýze. Konkrétně není obvykle důležité, zda chybový výraz sleduje normální rozdělení.

Vážené nejmenší čtverce

„Fanning Out“ Vliv heteroscedasticity

Zvláštní případ generalizovaných nejmenších čtverců, nazývaných vážené nejmenší čtverce, nastává, když jsou všechny off-diagonální záznamy Ω (korelační matice reziduí) nulové; rozptyly z pozorování (podél kovarianční matice diagonálně) může být stále nerovnoměrné ( heteroskedasticita ). Jednoduše řečeno, heteroscedasticita je, když rozptyl závisí na hodnotě, která způsobí, že zbytkový graf vytvoří efekt „rozdmýchávání“ směrem k větším hodnotám, jak je vidět na zbytkovém grafu vpravo. Na druhé straně homoscedasticita předpokládá, že rozptyl a je stejný. ${\ displaystyle Y_ {i}}$ ${\ displaystyle x_ {i}}$ ${\ displaystyle Y_ {i}}$ ${\ displaystyle Y_ {i}}$ ${\ displaystyle U_ {i}}$

Vztah k hlavním komponentám

První hlavní komponentu o průměru sady bodů lze znázornit přímkou, která se nejvíce blíží datovým bodům (měřeno čtvercovou vzdáleností nejbližšího přiblížení, tj. Kolmo na přímku). Naproti tomu lineární nejmenší čtverce se snaží minimalizovat vzdálenost pouze ve směru. Ačkoli tedy oba používají podobnou chybovou metriku, lineární nejmenší čtverce jsou metodou, která přednostně zachází s jednou dimenzí dat, zatímco PCA se všemi dimenzemi zachází stejně. ${\ displaystyle y}$

Teorie vztahu k měření

Významná statistička Sara van de Geer použila k prokázání odhadu nejmenších čtverců empirickou teorii procesů a dimenzi Vapnik-Chervonenkis jako měřítko prostoru čtvercově integrovatelných funkcí .

Regulace

Tichonovská regularizace

V některých kontextech může být upřednostňována regulovaná verze řešení s nejmenšími čtverci. Tikhonov regularizace (nebo hřebenová regrese ) přidává omezení, že se L ₂ -norm parametru vektoru, který není větší než daná hodnota. Ekvivalentně to může vyřešit neomezenou minimalizaci trestu nejmenších čtverců s přidanou, kde je konstanta (to je Lagrangeova forma omezeného problému). V Bayesovském kontextu je to ekvivalentní umístění nulového průměru normálně distribuovaného před na vektor parametru. ${\ displaystyle \ | \ beta \ |^{2}}$ ${\ Displaystyle \ alpha \ | \ beta \ |^{2}}$ ${\ Displaystyle \ alpha}$

Laso metoda

Alternativní upravená předpisy verze nejmenších čtverců je Lasso (alespoň absolutní smrštění a výběru operátora), který používá omezení, že se L ₁ -norm parametru vektoru, není větší než daná hodnota. (Jak je uvedeno výše, toto je ekvivalentní neomezené minimalizaci trestu nejmenších čtverců s přidáním.) V Bayesovském kontextu je to ekvivalentní umístění Laplaceovy předchozí distribuce s nulovým průměrem na vektor parametrů. Problém optimalizace lze vyřešit pomocí kvadratického programování nebo obecnějších konvexních optimalizačních metod, jakož i specifickými algoritmy, jako je algoritmus regrese s nejmenším úhlem . ${\ displaystyle \ | \ beta \ |}$ ${\ displaystyle \ alpha \ | \ beta \ |}$

Jeden z hlavních rozdílů mezi Lasso a hřebenovou regresí je ten, že při hřebenové regresi, jak se zvyšuje trest, jsou všechny parametry redukovány, zatímco stále zůstávají nenulové, zatímco v Lasso, zvyšování trestu způsobí, že bude stále více parametrů najeto na nulu. To je výhoda Lasso oproti hřebenové regresi, protože jízdní parametry na nulu zruší výběr funkcí z regrese. Lasso tedy automaticky vybírá relevantnější funkce a zahodí ostatní, zatímco regrese Ridge nikdy zcela nevyhodí žádné funkce. Některé techniky výběru funkcí jsou vyvinuty na základě LASSO, včetně Bolasso, který spouští vzorky, a FeaLect, který analyzuje regresní koeficienty odpovídající různým hodnotám, aby byly získány všechny funkce. ${\ Displaystyle \ alpha}$

L ¹ -regularized přípravek je užitečný v některých kontextech vzhledem ke své tendenci, aby dal přednost řešení, kde další parametry jsou nulové, což dává řešení, které závisí na menší počet proměnných. Z tohoto důvodu je Lasso a jeho varianty zásadní pro oblast stlačeného snímání . Rozšířením tohoto přístupu je elastická regularizace sítě .

Viz také

Reference

Další čtení

Björck, Å. (1996). Numerické metody pro problémy nejmenších čtverců . SIAM. ISBN 978-0-89871-360-2.
Kariya, T .; Kurata, H. (2004). Zobecněné nejmenší čtverce . Hoboken: Wiley. ISBN 978-0-470-86697-9.
Luenberger, DG (1997) [1969]. „Odhad nejmenších čtverců“ . Optimalizace metodami Vector Space . New York: John Wiley & Sons. s. 78–102. ISBN 978-0-471-18117-0.
Rao, ČR ; Toutenburg, H .; a kol. (2008). Lineární modely: nejmenší čtverce a alternativy . Springer Series ve statistikách (3. vyd.). Berlín: Springer. ISBN 978-3-540-74226-5.
Van de moortel, Koen (duben 2021). „Vícesměrná regresní analýza“ .
Wolberg, J. (2005). Analýza dat metodou nejmenších čtverců: extrahování většiny informací z experimentů . Berlín: Springer. ISBN 978-3-540-25674-8.

externí odkazy

Média související s nejmenšími čtverci na Wikimedia Commons

Languages

In other projects