Möbiova transformace - Möbius transformation
V geometrii a komplexní analýzy , je Möbius transformace v komplexní rovině je racionální funkce ve tvaru
Geometricky lze Möbiovu transformaci získat tak, že nejprve provedete stereografickou projekci z roviny do jednotkové dvou sféry , otočíte a přesunete kouli na nové místo a orientaci v prostoru a poté provedete stereografickou projekci (z nové polohy koule ) do letadla. Tyto transformace zachovávají úhly, mapují každou přímku na přímku nebo kruh a mapují každý kruh na čáru nebo kruh.
Transformace Möbius jsou projektivní transformace z komplexu projektivní linie . Tvoří skupinu zvanou Möbiusova skupina , což je projektivní lineární skupina PGL (2, C ). Spolu se svými podskupinami má mnoho aplikací v matematice a fyzice.
Möbiusovy transformace jsou pojmenovány na počest Augusta Ferdinanda Möbia ; jsou také různě pojmenovány homografie , homografické transformace , lineární zlomkové transformace , bilineární transformace , frakční lineární transformace nebo spinové transformace (teorie relativity) .
Přehled
Möbiusovy transformace jsou definovány na rozšířené komplexní rovině (tj. Komplexní rovině rozšířené o bod v nekonečnu ).
Stereografická projekce se identifikuje s koulí, která se pak nazývá Riemannova koule ; alternativně si jej lze představit jako komplexní projektivní linii . Möbiovy transformace jsou přesně bijektivní konformní mapy z Riemannovy sféry k sobě, tj. Automorfismy Riemannovy sféry jako komplexního potrubí ; alternativně jsou to automorfismy jako algebraické odrůdy. Proto soubor všech Möbiových transformací tvoří skupinu pod kompozicí . Tato skupina se nazývá skupina Möbius a je někdy označována .
Skupina Möbius je isomorphic ke skupině orientace-chránit isometries z hyperbolického 3-prostor , a proto hraje důležitou roli při studiu hyperbolické 3-manifolds .
Ve fyzice se složka identita na Lorentzovy grupy působí na nebeské sféry stejným způsobem, že skupina Möbiovo působí na Riemann koule. Ve skutečnosti jsou tyto dvě skupiny izomorfní. Pozorovatel, který zrychluje na relativistické rychlosti, uvidí průběh souhvězdí pozorovaný v blízkosti Země kontinuálně transformovat podle nekonečně malých Möbiových transformací. Toto pozorování je často bráno jako výchozí bod twistorové teorie .
Některé podskupiny skupiny Möbius tvoří skupiny automorfismu ostatních jednoduše spojených povrchů Riemann ( komplexní rovina a hyperbolická rovina ). Möbiusovy transformace jako takové hrají důležitou roli v teorii Riemannových povrchů . Základní skupina každé Riemann povrchu je diskrétní podskupina skupiny Möbius (viz Fuchsian skupinu a skupinu Kleinian ). Obzvláště důležitou diskrétní podskupinou skupiny Möbius je modulární skupina ; je ústřední pro teorii mnoha fraktálů , modulárních forem , eliptických křivek a Pellianových rovnic .
Möbiovy transformace lze obecněji definovat v prostorech dimenze n > 2 jako bijektivní mapy zachovávající konformní orientaci z n -sféry do n -sféry. Taková transformace je nejobecnější formou konformního mapování domény. Podle Liouvilleovy věty lze Möbiovu transformaci vyjádřit jako složení překladů, podobností , ortogonálních transformací a inverzí.
Definice
Obecná forma Möbiovy transformace je dána vztahem
V případě c ≠ 0 je tato definice rozšířena na celou Riemannovu sféru definováním
Pokud c = 0 , definujeme
Möbiova transformace je tedy vždy bijektivní holomorfní funkcí z Riemannovy sféry do Riemannovy sféry.
Soubor všech Möbiových transformací tvoří skupinu pod kompozicí . Této skupině lze dát strukturu komplexního potrubí takovým způsobem, že kompozice a inverze jsou holomorfní mapy . Skupina Möbius je pak složitá Lieova skupina . Skupina Möbius je obvykle označována jako automorfistická skupina Riemannovy sféry.
Pevné body
Každá Möbiova transformace bez identity má dva pevné body na Riemannově sféře. Všimněte si, že pevné body se zde počítají s multiplicitou ; parabolické transformace jsou ty, kde se pevné body shodují. Jeden nebo oba tyto pevné body mohou být bodem v nekonečnu.
Určení pevných bodů
Pevné body transformace
Když c = 0, kvadratická rovnice degeneruje do lineární rovnice a transformace je lineární. To odpovídá situaci, že jedním z pevných bodů je bod v nekonečnu. Když je ≠ d, druhý pevný bod je konečný a je dán vztahem
V tomto případě bude transformací jednoduchá transformace složená z překladů , rotací a dilatací :
Pokud c = 0 a a = d , pak jsou oba pevné body v nekonečnu a Möbiova transformace odpovídá čistému překladu:
Topologický důkaz
Topologicky skutečnost, že (neidentifikační) Möbiovy transformace fixují 2 body (s multiplicitou), odpovídá Eulerově charakteristice sféry, která je 2:
Za prvé, projektivní lineární skupina PGL (2, K ) je ostře 3-tranzitivní -pro jakékoli dvě uspořádané trojice odlišných bodů existuje jedinečná mapa, která převádí jednu trojici na druhou, stejně jako u Möbiusových transformací, a tímtéž algebraický důkaz (v podstatě počítání dimenzí , protože skupina je 3-dimenzionální). Identitou je tedy jakákoli mapa, která opravuje alespoň 3 body.
Dále lze podle identifikace skupiny Möbius zjistit, že jakákoli funkce Möbius je homotopická k identitě. Ve skutečnosti může být jakýkoli člen obecné lineární skupiny redukován na mapu identity Gauss-Jordanovou eliminací, což ukazuje, že projektivní lineární skupina je také propojena s cestou a poskytuje homotopii k mapě identity. Lefschetz-Hopf teorém říká, že součet indexů (v této souvislosti, multiplicita) pevné body mapy se konečně mnoha pevných bodů se rovná počtu Lefschetz mapy, která je v tomto případě stopa mapy identity na homologických skupinách, což je prostě Eulerova charakteristika.
Naproti tomu projektivní lineární skupina skutečné projektivní linie PGL (2, R ) nemusí opravovat žádné body - například nemá žádné (skutečné) pevné body: jako komplexní transformace opravuje ± i - zatímco mapa 2 x opravuje dva body 0 a ∞. To odpovídá skutečnosti, že Eulerova charakteristika kruhu (skutečná projektivní přímka) je 0, a proto Lefschetzova věta o pevných bodech říká pouze to, že musí opravit alespoň 0 bodů, ale možná i více.
Normální forma
Möbiusovy transformace jsou také někdy psány z hlediska jejich pevných bodů v takzvané normální formě . Nejprve ošetříme neparabolický případ, pro který existují dva odlišné pevné body.
Neparabolický případ :
Každá neparabobická transformace je konjugována k dilataci/rotaci, tj. Transformaci formy
Pokud f má výrazné pevné body ( γ 1 , y 2 ), pak transformace má pevnou bodů při 0 ° C a ∞, a je tedy dilatace: . Potom lze zapsat rovnici pevného bodu pro transformaci f
Řešení pro f dává (ve formě matice):
Z výše uvedených výrazů lze vypočítat derivace f v pevných bodech:
Všimněte si, že, vzhledem k tomu, objednávání pevných bodů, můžeme rozlišit jeden z násobičky ( k- ) z f jako charakteristickou konstantou o f . Obrácení pořadí pevných bodů je ekvivalentní převzetí inverzního multiplikátoru pro charakteristickou konstantu:
Pro loxodromické transformace, kdykoli | k | > 1, říká se, že γ 1 je odpudivý pevný bod a γ 2 je atraktivní pevný bod. Pro | k | <1, role jsou obráceny.
Parabolický případ :
V parabolickém případě existuje pouze jeden pevný bod γ . Transformace odesílající tento bod do ∞ je
Zde se β nazývá délka překladu . Vzorec pevného bodu pro parabolickou transformaci je pak
Řešení pro f (ve formě matice) dává
Všimněte si, že β je není charakteristická konstanta F , který je vždy 1 pro parabolické transformaci. Z výše uvedených výrazů lze vypočítat:
Póly transformace
Jde o to se nazývá pole of ; je to ten bod, který je transformován do bodu v nekonečnu pod .
Inverzní pól je bod, do kterého se transformuje bod v nekonečnu. Bod uprostřed mezi dvěma póly je vždy stejný jako bod uprostřed mezi dvěma pevnými body:
Tyto čtyři body jsou vrcholy rovnoběžníku, kterému se někdy říká charakteristický rovnoběžník transformace.
Transformaci lze specifikovat dvěma pevnými body γ 1 , γ 2 a pólem .
To nám umožňuje odvodit vzorec pro převod mezi k a daným :
Poslední výraz se shoduje s jedním z (vzájemně recipročních) poměrů vlastních čísel matice
Jednoduché Möbiusovy transformace a kompozice
Möbiova transformace může být složena jako sled jednoduchých transformací.
Následující jednoduché transformace jsou také Möbiusovy transformace:
- je překlad .
- je kombinací a ( homothety a rotace ). Pokud je to tedy rotace, pokud je to homothety.
- ( inverze a reflexe vzhledem ke skutečné ose)
Složení jednoduchých transformací
Pokud , nechte:
- ( Překlad podle d / c )
- ( inverze a reflexe vzhledem ke skutečné ose)
- ( homothety a rotace )
- (překlad a / c )
Pak lze tyto funkce skládat , dávat
To znamená,
Díky tomuto rozkladu je zřejmé mnoho vlastností Möbiovy transformace.
Elementární vlastnosti
Möbiova transformace je ekvivalentní sekvenci jednodušších transformací. Složení ukazuje mnoho vlastností Möbiovy transformace.
Vzorec pro inverzní transformaci
Existenci inverzní Möbiovy transformace a její explicitní vzorec lze snadno odvodit složením inverzních funkcí jednodušších transformací. To znamená, definujte funkce g 1 , g 2 , g 3 , g 4 tak, že každé g i je inverzní k f i . Pak složení
Zachování úhlů a zobecněných kruhů
Z tohoto rozkladu vidíme, že Möbiovy transformace přenášejí všechny netriviální vlastnosti kruhové inverze . Například zachování úhlů je redukováno na prokázání, že kruhová inverze zachovává úhly, protože ostatní typy transformací jsou dilatace a izometrie (translace, reflexe, rotace), které triviálně zachovávají úhly.
Kromě toho Möbiusovy transformace mapují generalizované kruhy na generalizované kruhy, protože inverze kruhu má tuto vlastnost. Zobecněný kruh je buď kruh nebo čára, přičemž druhá je považována za kružnici procházející bodem v nekonečnu. Pamatujte, že Möbiova transformace nemusí nutně mapovat kruhy na kruhy a čáry na čáry: může je kombinovat. I když mapuje kruh na jiný kruh, nemusí nutně mapovat střed prvního kruhu na střed druhého kruhu.
Zachování křížového poměru
Křížové poměry jsou pod Möbiusovými transformacemi neměnné. To znamená, že pokud Möbiova transformace mapuje čtyři různé body na čtyři odlišné body , pak
Pokud je jedním z bodů bod v nekonečnu, musí být příčný poměr definován přijetím příslušného limitu; např. křížový poměr je
Křížový poměr čtyř různých bodů je skutečný právě tehdy, když jimi prochází čára nebo kruh. Je to další způsob, jak ukázat, že Möbiusovy transformace zachovávají zobecněné kruhy.
Časování
Dva body z 1 a z 2 jsou spojeny s ohledem na zobecněnou kružnici C , pokud je dána zobecněná kružnice D procházející z 1 a z 2 a řezající C ve dvou bodech a a b , ( z 1 , z 2 ; a , b ) jsou v harmonickém křížovém poměru (tj. jejich křížový poměr je −1). Tato vlastnost nezávisí na volbě kružnice D . Tato vlastnost je také někdy označována jako symetrická vzhledem k přímce nebo kružnici.
Dva body z , z ∗ jsou sdružené vzhledem k přímce, pokud jsou symetrické vzhledem k přímce. Dva body jsou spojeny vzhledem ke kruhu, pokud jsou vyměněny inverzí vzhledem k tomuto kruhu.
Bod z ∗ konjugovaný k z, když L je přímka určená vektorem e iθ v bodě z 0, lze explicitně zadat jako
Bod z ∗ konjugovaný k z, když C je kruh o poloměru r se středem z 0, lze explicitně zadat jako
Protože Möbiusovy transformace zachovávají zobecněné kruhy a křížové poměry, zachovávají také konjugaci.
Projektivní maticové reprezentace
Přirozené působení PGL (2, C ) na komplexní projektivní linii CP 1 je přesně přirozené působení skupiny Möbius na Riemannovu sféru, kde projektivní linie CP 1 a Riemannova sféra jsou identifikovány následovně:
S každým invertibilním komplexem 2 × 2 matice
Je snadné zkontrolovat, že pak bude součin dvou matic spojen se složením dvou odpovídajících Möbiusových transformací. Jinými slovy, mapa
Všimněte si, že jakákoli matice získaná vynásobením komplexním skalárem λ určuje stejnou transformaci, takže Möbiova transformace určuje její matici pouze
do skalárních násobků. Jinými slovy: ZAŘÍZENÍ jádro z n se skládá ze všech skalárních násobků identita matice I , a první izomorfizmu teorém teorie skupina uvádí, že kvocient skupina GL (2, C ) / (( C \ {0}) I ) je izomorfní ke skupině Möbius. Tato kvocientová skupina je známá jako projektivní lineární skupina a obvykle se označuje PGL (2, C ).Omezíme -li se na matice určující jedničky, mapa
π se omezí na surjektivní mapu ze speciální lineární skupiny SL (2, C ) do skupiny Möbius; v omezeném nastavení je jádro tvořeno plusem a mínusem identity a kvocientová skupina SL (2, C ) / {± I }, označená PSL (2, C ), je tedy také izomorfní vůči skupině Möbius:Všimněte si, že existují přesně dvě matice s jednotkovým determinantem, které lze použít k reprezentaci jakékoli dané Möbiovy transformace. To znamená, že SL (2, C ) je dvojitý kryt PSL (2, C ). Protože je SL (2, C ) jednoduše připojen , je univerzálním krytem skupiny Möbius. Proto je základní skupina skupiny Möbius je Z 2 .
Určení transformace třemi body
Vzhledem k množině tří odlišných bodů z 1 , z 2 , z 3 na Riemannově kouli a druhé sadě odlišných bodů w 1 , w 2 , w 3 existuje přesně jedna Möbiova transformace f ( z ) s f ( z i ) = w i pro i = 1,2,3. (Jinými slovy: působení skupiny Möbius na Riemannovu sféru je ostře 3-tranzitivní .) Existuje několik způsobů, jak z daných množin bodů určit f ( z ).
Mapování nejprve na 0, 1, ∞
Je snadné ověřit, že Möbiova transformace
Pokud je podobně definováno pro mapu
w 1 , w 2 , w 3 až 0, 1, ∞, pak se matice, která mapuje z 1,2,3 až w 1,2,3, staneStabilizátor {0, 1, ∞} (jako neuspořádaná množina) je podskupina známá jako anharmonická skupina .
Explicitní determinantní vzorec
Rovnice
Podskupiny skupiny Möbius
Pokud požadujeme, aby koeficienty a , b , c , d Möbiovy transformace byla reálná čísla s ad - bc = 1 , získáme podskupinu Möbiusovy skupiny označenou jako PSL (2, R ) . Toto je skupina těch Möbiových transformací, které mapují horní polorovinu H = x + i y : y > 0 na sebe, a je rovna skupině všech biholomorfních (nebo ekvivalentně: bijektivních , konformních a orientačně zachovávajících) map H → H . Pokud je zavedena správná metrika , horní polorovina se stane modelem hyperbolické roviny H 2 , Poincarého poloroviny a PSL (2, R ) je skupina všech izometrií zachovávajících orientaci H 2 v tomto Modelka.
Podskupina všech Möbiusových transformací, které mapují otevřený disk D = z : | z | <1 k sobě se skládá ze všech transformací formuláře
Protože obě výše uvedené podskupiny slouží jako izometrické skupiny H 2 , jsou izomorfní. Konjugací s transformací je dán konkrétní izomorfismus
Alternativně zvažte otevřený disk s poloměrem r se středem v r i . Poincaréův model disku na tomto disku se stane identickým s modelem horní poloviny roviny, když se r blíží ∞.
Maximální kompaktní podskupina skupiny Möbius je dána (
Tóth 2002 )Icosahedrální skupiny Möbiusových transformací použil Felix Klein k poskytnutí analytického řešení kvintické rovnice v ( Klein 1888 ); moderní expozice je uvedena v ( Tóth 2002 ).
Pokud požadujeme, aby koeficienty a , b , c , d Möbiovy transformace byly celá čísla s ad - bc = 1, získáme modulární skupinu PSL (2, Z ), diskrétní podskupinu PSL (2, R ) důležitou v studium mřížek v komplexní rovině, eliptických funkcí a eliptických křivek . Diskrétní podskupiny PSL (2, R ) jsou známé jako fuchsijské skupiny ; jsou důležité při studiu Riemannových povrchů .
Klasifikace

V následující diskusi budeme vždy předpokládat, že reprezentující matice je normalizována tak, že .
Non-identity Möbius transformace jsou běžně klasifikovány do čtyř typů, parabolické , eliptické , hyperbolické a loxodromické , přičemž hyperbolické jsou podtřídou loxodromických. Klasifikace má algebraický i geometrický význam. Geometricky, různé typy mají za následek různé transformace komplexní roviny, jak ukazují obrázky níže.
Tyto čtyři typy lze odlišit pohledem na stopu . Všimněte si, že trasování je neměnné v
konjugaci , tj.Parabolické transformace
Neidentifikovaná Möbiova transformace definovaná maticí determinantní je prý
parabolická, pokudMnožina všech parabolických Möbiových transformací s daným pevným bodem v , spolu s identitou, tvoří podskupinu izomorfní ke skupině matic
Charakteristická konstanta
Všechny neparabolické transformace mají dva pevné body a jsou definovány maticí spojenou s
Eliptické transformace

Transformace se říká, že eliptická , pokud může být reprezentován maticí , jehož stopa je skutečný s
Transformace je eliptická právě tehdy, když | λ | = 1 a λ ≠ ± 1. Při psaní je spojena eliptická transformace
Všimněte si, že pro jakýkoli s charakteristickou konstantní k je charakteristická konstanta je k n . Všechny Möbiovy transformace konečného řádu jsou tedy eliptické transformace, konkrétně přesně ty, kde λ je kořenem jednoty , nebo ekvivalentně kde α je racionální násobek π . Nejjednodušší možnost zlomkového násobku znamená α = π /2, což je také jedinečný případ , se také označuje jako kruhová transformace ; to geometricky odpovídá otáčení o 180 ° kolem dvou pevných bodů. Tato třída je ve formě matice reprezentována jako:
Hyperbolické transformace
Transformační se říká, že hyperbolické , pokud může být reprezentován maticí , jehož stopa je
skutečný sTransformace je hyperbolická právě tehdy, je -li λ skutečná a λ ≠ ± 1.
Loxodromické transformace
Transformace je loxodromická, pokud není v [0,4]. Transformace je loxodromická právě tehdy, když .
Historicky, navigace podle loxodrome nebo loxodromy odkazuje na dráze konstantní ložiska ; výsledná cesta je logaritmická spirála , tvarem podobná transformacím komplexní roviny, kterou vytváří loxodromická Möbiova transformace. Viz níže geometrické obrázky.
Obecná klasifikace
| Proměna | Trace na druhou | Multiplikátory | Zástupce třídy | |
|---|---|---|---|---|
| Oběžník | σ = 0 | k = −1 | z ↦ - z | |
| Eliptický | 0 ≤ σ <4 | | k | = 1 | z ↦ e i θ z | |
| Parabolický | σ = 4 | k = 1 | z ↦ z + a | |
| Hyperbolický | 4 <σ <∞ | z ↦ e θ z | ||
| Loxodromic | σ ∈ C \ [0,4] | z ↦ kz | ||
Skutečný případ a poznámka k terminologii
Nad reálnými čísly (pokud musí být koeficienty reálné) neexistují žádné nehyperbolické loxodromické transformace a klasifikace je na eliptické, parabolické a hyperbolické, jako pro skutečné kužely . Terminologie je kvůli zvažuje polovinu absolutní hodnotu trasování | tr | / 2, jako výstřednost transformace - dělení 2 koriguje dimenzi, takže identita má výstřednost 1 (tr / n je někdy používán jako alternativa pro stopu z tohoto důvodu) a absolutní hodnota koriguje, že stopa je definována pouze do faktoru ± 1 kvůli práci v PSL. Alternativně lze použít polovinu stopy na druhou jako proxy pro druhou mocninu excentricity, jak bylo provedeno výše; tyto klasifikace (ale ne přesné hodnoty excentricity, protože kvadratura a absolutní hodnoty jsou různé) souhlasí se skutečnými stopami, ale ne s komplexními stopami. Stejná terminologie se používá pro klasifikaci prvků SL (2, R ) (2násobný obal) a analogické klasifikace se používají jinde. Loxodromické transformace jsou v podstatě komplexním jevem a odpovídají komplexním excentricitám.
Geometrická interpretace charakteristické konstanty
Následující obrázek zobrazuje (po stereografické transformaci z koule do roviny) dva pevné body Möbiovy transformace v neparabolickém případě:
Charakteristickou konstantu lze vyjádřit logaritmem :
Eliptické transformace
Pokud ρ = 0, pak pevné body nejsou ani atraktivní ani odpudivé, ale lhostejné, a transformace je prý eliptická . Tyto transformace mají tendenci přesouvat všechny body v kruzích kolem dvou pevných bodů. Pokud je jeden z pevných bodů v nekonečnu, je to ekvivalentní afinní rotaci kolem bodu.
Pokud vezmeme podskupinu s
jedním parametrem generovanou jakoukoli eliptickou Möbiusovou transformací, získáme spojitou transformaci, takže každá transformace v podskupině fixuje stejné dva body. Všechny ostatní body proudí podél rodiny kruhů, které jsou vnořeny mezi dva pevné body na Riemannově kouli. Obecně mohou být dva pevné body libovolné dva odlišné body.To má důležitou fyzickou interpretaci. Představte si, že se nějaký pozorovatel otáčí konstantní úhlovou rychlostí kolem nějaké osy. Pak můžeme dva pevné body považovat za severní a jižní pól nebeské sféry. Vzhled noční oblohy je nyní kontinuálně transformován přesně způsobem popsaným jednoparametrovou podskupinou eliptických transformací sdílejících pevné body 0, ∞ a s číslem α odpovídajícím konstantní úhlové rychlosti našeho pozorovatele.
Zde je několik obrázků ilustrujících účinek eliptické Möbiovy transformace na Riemannovu sféru (po stereografické projekci do roviny):
Tyto obrázky ilustrují účinek jediné Möbiovy transformace. Jednoparametrická podskupina, kterou generuje, nepřetržitě pohybuje body podél rodiny kruhových oblouků navržených obrázky.
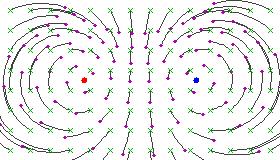
Hyperbolické transformace
Pokud je α nula (nebo násobek 2 π ), pak je transformace označena jako
hyperbolická . Tyto transformace mají tendenci pohybovat body po kruhových drahách od jednoho pevného bodu k druhému.Pokud vezmeme podskupinu s
jedním parametrem generovanou jakoukoli hyperbolickou Möbiusovou transformací, získáme spojitou transformaci, takže každá transformace v podskupině fixuje stejné dva body. Všechny ostatní body proudit podél určité skupiny kruhových oblouků pryč od prvního pevného bodu a k druhému pevnému bodu. Obecně mohou být dva pevné body libovolné dva odlišné body na Riemannově kouli.I toto má důležitou fyzickou interpretaci. Představte si, že pozorovatel zrychluje (s konstantní velikostí zrychlení) ve směru severního pólu na své nebeské sféře. Poté se vzhled noční oblohy transformuje přesně způsobem popsaným jednoparametrovou podskupinou hyperbolických transformací sdílejících pevné body 0, ∞, přičemž skutečné číslo ρ odpovídá velikosti jeho zrychlovacího vektoru. Zdá se, že se hvězdy pohybují po délkách, od jižního pólu směrem k severnímu pólu. (Zeměpisné délky se při stereografickém promítání ze sféry do roviny zobrazují jako kruhové oblouky.)
Zde je několik obrázků ilustrujících účinek hyperbolické Möbiovy transformace na Riemannovu sféru (po stereografické projekci do roviny):
Tyto obrázky připomínají siločáry kladného a záporného elektrického náboje umístěné v pevných bodech, protože kruhové linie toku svírají mezi dvěma pevnými body konstantní úhel.
Loxodromické transformace
Pokud jsou ρ i α nenulové, pak se říká, že transformace je loxodromická . Tyto transformace mají tendenci přesouvat všechny body v drahách ve tvaru S z jednoho pevného bodu do druhého.
Slovo „ loxodrome “ je z řečtiny: „λοξος (loxos), šikmé + δρόμος (dromos), kurz “. Při plachtění na konstantní ložiska - pokud si udržet záhlaví (řekněme) na sever-východ, budete nakonec skončit plavbu kolem severního pólu v logaritmické spirály . Na mercatorové projekci je takový kurz přímkou, protože severní a jižní pól se promítají do nekonečna. Úhel, který loxodrom svírá vzhledem k délkovým čarám (tj. Jeho sklon, „těsnost“ spirály), je argumentem k . Transformace Möbius samozřejmě mohou mít své dva pevné body kdekoli, nejen na severním a jižním pólu. Ale jakákoli loxodromická transformace bude konjugována s transformací, která přesune všechny body podél takových loxodromů.
Pokud vezmeme podskupinu s
jedním parametrem generovanou jakoukoli loxodromickou Möbiusovou transformací, získáme spojitou transformaci, takže každá transformace v podskupině fixuje stejné dva body. Všechny ostatní body proudí podél určité rodiny křivek, pryč od prvního pevného bodu a směrem k druhému pevnému bodu. Na rozdíl od hyperbolického případu nejsou tyto křivky kruhovými oblouky, ale určitými křivkami, které se při stereografickém promítání z koule do roviny objevují jako spirálové křivky, které se otáčejí proti směru hodinových ručiček nekonečně často kolem jednoho pevného bodu a otáčejí se ve směru hodinových ručiček nekonečně často kolem druhého pevného bodu. Obecně mohou být dva pevné body libovolné dva odlišné body na Riemannově kouli.Fyzickou interpretaci můžete pravděpodobně uhodnout v případě, kdy jsou dva pevné body 0, ∞: pozorovatel, který se otáčí (s konstantní úhlovou rychlostí) kolem nějaké osy a pohybuje se podél stejné osy, uvidí vzhled noční oblohy transformovat podle jednoparametrické podskupiny loxodromických transformací s pevnými body 0, ∞ a ρ, α určenými příslušně velikostí skutečných lineárních a úhlových rychlostí.
Stereografická projekce
Tyto obrázky ukazují Möbiovy transformace stereograficky promítnuté do Riemannovy sféry . Zejména si všimněte, že při promítnutí na kouli se zvláštní případ pevného bodu v nekonečnu nijak neliší od toho, že má pevné body v libovolném místě.
| Jeden pevný bod v nekonečnu | ||
| Pevné body diametrálně protilehlé | ||
| Pevné body na libovolném místě | ||
Iterace transformace
Pokud má transformace pevné body γ
1 , γ 2 a charakteristickou konstantu k , pak bude mít .To lze použít k iteraci transformace nebo k její animaci rozdělením na kroky.
Tyto obrázky ukazují tři body (červený, modrý a černý) nepřetržitě iterované v transformacích s různými charakteristickými konstantami.
 |
 |
 |
|
A tyto obrázky ukazují, co se stane, když transformujete kruh pod transformacemi Hyperbolic, Eliptical a Loxodromic. Všimněte si, že na eliptických a loxodromických obrázcích je hodnota α 1/10.
Vyšší rozměry
Ve vyšších dimenzích, je Möbius transformace je homeomorfismus z je
jednobodová kompaktifikace z , což je konečné složení inverzí v oblastech a odrazy v nadrovin . Liouvilleova věta v konformní geometrii uvádí, že v dimenzi alespoň tři jsou všechny konformní transformace Möbiovy transformace. Každá Möbiova transformace může být vložena do formykde , , je
ortogonální matice , a je 0 nebo 2. skupina Möbius transformace se také nazývá skupina Möbius .Orientace zachovávající Möbiovy transformace tvoří spojenou složku identity ve skupině Möbius. V dimenzi n = 2 jsou Möbiovy transformace zachovávající orientaci přesně mapy zde pokryté Riemannovy sféry. Ty, které mění orientaci, se z nich získají komplexní konjugací.
Doména Möbiových transformací, tj . Je homeomorfní pro
n -dimenzionální sféru . Kanonický izomorfismus mezi těmito dvěma prostory je Cayleyova transformace , která je sama o sobě Möbiova transformací . Tato identifikace znamená, že Möbiovy transformace lze také považovat za konformní izomorfismy . N -sphere, spolu s působením skupiny Möbius, je geometrická struktura (ve smyslu Kleina programu Erlangen ) s názvem Möbius geometrie .Aplikace
Lorentzova transformace
Několik autorů zaznamenalo izomorfismus skupiny Möbius se skupinou Lorentz : Na základě předchozích prací Felixe Kleina (1893, 1897) o automorfních funkcích souvisejících s hyperbolickou geometrií a Möbiusovou geometrií
Gustav Herglotz (1909) ukázal, že hyperbolické pohyby (tj. izometrické automorfismy příslušníky hyperbolického prostoru ) transformaci koule jednotky do sebe odpovídají Lorentz transformacemi, kterými Herglotz byl schopen zařadit jeden parametr Lorentz transformace do loxodromic, eliptické, hyperbolické a parabolické skupin. Mezi další autory patří Emil Artin (1957), HSM Coxeter (1965) a Roger Penrose , Wolfgang Rindler (1984), Tristan Needham (1997) a WM Olivia (2002).Minkowského prostor se skládá ze čtyřrozměrného reálného souřadnicového prostoru R 4, který se skládá z prostoru uspořádaných čtyřnásobků ( x 0 , x 1 , x 2 , x 3 ) reálných čísel, spolu s kvadratickou formou
Půjčování terminologie ze speciální relativity , body s Q > 0 jsou považovány za časové ; navíc, pokud x 0 > 0 , pak se tento bod nazývá směřující do budoucnosti . Body s Q <0 se nazývají prostorové . Null kužel S sestává z těch míst, kde Q = 0 ; budoucí null kužel N + jsou ty body na nulový kužel s x 0 > 0 . Nebeské sféry je pak identifikován sběr záření v N + , jehož výchozím bodem je původ R 4 . Sbírka lineárních transformací na R 4 s pozitivním determinantem zachovávajícím kvadratickou formu Q a zachovávajícím časový směr tvoří omezenou Lorentzovu skupinu SO + (1,3).
V souvislosti s geometrií nebeské sféry je skupina transformací SO + (1,3) ztotožněna se skupinou PSL (2, C ) Möbiových transformací sféry. Do každé ( x 0 , x 1 , x 2 , x 3 ) ∈ R 4 , přidružit Hermitovské matrici
Determinant z matice X se rovná Q ( x 0 , x 1 , x 2 , x 3 ) . Speciální lineární skupina působí na ploše těchto matric přes
-
( 1 )
pro každé A ∈ SL (2, C ), a toto působení SL (2, C ) zachovává determinant X, protože det A = 1 . Protože determinant X je identifikován s kvadratickou formou Q , SL (2, C ) působí Lorentzovými transformacemi. Z rozměrových důvodů SL (2, C ) pokrývá sousedství identity SO (1,3). Protože je připojen SL (2, C ), pokrývá celou omezenou Lorentzovu skupinu SO + (1,3). Kromě toho, protože jádro akce ( 1 ) je podskupina {± I }, pak přechod do kvocientové skupiny dává skupině izomorfismus
-
( 2 )
Nyní se zaměříme na případ, kdy ( x 0 , x 1 , x 2 , x 3 ) je null, matice X má nulový determinant, a proto se rozděluje jako vnější produkt komplexního dvou vektoru ξ s jeho komplexním konjugátem:
-
( 3 )
Na dvousložkový vektor ξ působí SL (2, C ) způsobem kompatibilním s ( 1 ). Nyní je jasné, že jádro reprezentace SL (2, C ) na poustevnických maticích je {± I }.
Účinek PSL (2, C ) na nebeskou sféru lze také popsat geometricky pomocí stereografické projekce . Nejprve zvažte hyperplanu v R 4 danou x 0 = 1. Nebeskou sféru lze identifikovat se sférou S + průsečíku hyperplany s budoucím nulovým kuželem N + . Stereografická projekce ze severního pólu (1,0,0,1) této koule do roviny x 3 = 0 vezme bod se souřadnicemi (1, x 1 , x 2 , x 3 ) s
Představujeme komplexní souřadnici
-
( 4 )
Působení SO + (1,3) na body N + nezachová hyperplanu S + , ale působí na body v S + a poté změní měřítko tak, že výsledek je opět v S +, dává akci SO + ( 1,3) na sféře, která přejde k akci na komplexní proměnné ζ. Ve skutečnosti je tato akce způsobena zlomkovými lineárními transformacemi, i když to z této reprezentace nebeské sféry není snadné vidět. Naopak, pro každou frakční lineární transformaci proměnné ζ přechází na jedinečnou Lorentzovu transformaci na N + , případně po vhodném (jedinečně určeném) změně měřítka.
Více invariantní popis stereografické projekce, který umožňuje, aby byla akce jasnější, je uvažovat proměnnou ζ = z : w jako poměr dvojice homogenních souřadnic pro komplexní projektivní přímku CP 1 . Stereografická projekce přechází do transformace z C 2 - {0} na N +, která je homogenní stupně dva s ohledem na skutečné škálování
-
( 5 )
který souhlasí s ( 4 ) po omezení na stupnice, ve kterých jsou složkami (
5 ) přesně ty, které jsou získány z vnějšího produktuStručně řečeno, činnost omezené Lorentzovy skupiny SO + (1,3) souhlasí s činností skupiny Möbius PSL (2, C ). To motivuje následující definici. V rozměru n ≥ 2 je Möbiova skupina Möb ( n ) skupina všech konformních izometrií zachovávajících orientaci kulaté koule S n sama k sobě. Realizací konformní sféry jako prostoru budoucích paprsků nulového kužele v Minkowského prostoru R 1, n +1 dojde k izomorfismu Möb ( n ) s omezenou Lorentzovou skupinou SO + (1, n +1 ) Lorentzových transformací s pozitivním determinantem, zachovávajícím směr času.
Coxeter místo toho začal s ekvivalentní kvadratickou formou
Skupinu Lorentz identifikoval s transformacemi, pro které je { x : Q ( x ) = -1} stabilní . Poté interpretoval x jako homogenní souřadnice a { x : Q ( x ) = 0}, nulový kužel , jako Cayleyovo absolutum pro hyperbolický prostor bodů { x : Q ( x ) <0}. Dále Coxeter představil proměnné
takže Lorentzův invariantní kvadrik odpovídá sféře Coxeter poznamenává, že o této korespondenci psal i
Felix Klein , přičemž do komplexní roviny použil stereografickou projekci z (0, 0, 1). Coxeter využil skutečnosti, že kruhy inverzní roviny představují roviny hyperbolický prostor a obecná homografie je produktem inverzí ve dvou nebo čtyřech kruzích, což odpovídá obecnému hyperbolickému posunutí, které je produktem inverzí ve dvou nebo čtyřech rovinách.Hyperbolický prostor
Jak je vidět výše, Möbiova skupina PSL (2, C ) působí na Minkowského prostor jako skupina těch izometrií, které zachovávají původ, orientaci prostoru a směr času. Omezíme-li se na body, kde Q = 1 v kuželu pozitivního světla, které tvoří model hyperbolického 3prostorového H 3 , vidíme, že skupina Möbius působí na H 3 jako skupina izometrií zachovávajících orientaci. Ve skutečnosti je skupina Möbius stejná jako skupina izometrií zachovávajících orientaci hyperbolického 3-prostoru.
Pokud použijeme model Poincaréovy koule , identifikující jednotkovou kouli v R 3 pomocí H 3 , pak můžeme uvažovat o Riemannově sféře jako o „konformní hranici“ H 3 . Každá izometrie zachovávající orientaci H 3 vede k Möbiově transformaci na Riemannově sféře a naopak; toto je úplně první pozorování vedoucí k dohadům o korespondenci AdS/CFT ve fyzice.
Viz také
- Bilineární transformace
- Konformní geometrie
- Fuchsijská skupina
- Zobecněný kruh
- Hyperbolická geometrie
- Nekonečné kompozice analytických funkcí
- Inverzní transformace
- Kleinianova skupina
- Geometrie koule lži
- Lineární frakční transformace
- Liouvilleova věta (konformní zobrazení)
- Lorentzova skupina
- Modulární skupina
- Poincaré model poloviční roviny
- Projektivní geometrie
- Projektivní čára přes prsten
- Teorie reprezentace skupiny Lorentz
Poznámky
Reference
Charakteristický
Všeobecné
- Arnold, Douglas N .; Rogness, Jonathan (2008), „Möbius Transformations Revealed“ (PDF) , Notices of the AMS , 55 (10): 1226–1231
- Beardon, Alan F. (1995), Geometrie diskrétních skupin , New York: Springer-Verlag, ISBN 978-0-387-90788-8
- Hall, GS (2004), Symetrie a struktura zakřivení v obecné relativitě , Singapur: World Scientific, ISBN 978-981-02-1051-9 (Klasifikaci Lieových subalgeber ze Lieovy algebry skupiny Lorentz viz kapitola 6 až do konjugace.)
- Katok, Svetlana (1992), Fuchsian Groups , Chicago: University of Chicago Press, ISBN 978-0-226-42583-2 Viz kapitola 2 .
- Klein, Felix (1888), Přednášky o ikosahedronu a řešení rovnic pátého stupně (Dover ed.), ISBN 978-0-486-49528-6.
- Knopp, Konrad (1952), Elements of the Theory of Functions , New York: Dover, ISBN 978-0-486-60154-0 (Krásný úvod do Riemannovy sféry, stereografická projekce a Möbiovy transformace najdete v kapitolách 3–5 této klasické knihy.)
- Mumford, David ; Série, Caroline; Wright, David (2002), Indra's Pearls: The Vision of Felix Klein , Cambridge University Press, ISBN 978-0-521-35253-6 (Zaměřeno na nematematiky, poskytuje vynikající výklad teorie a výsledků, bohatě ilustrovaný diagramy.)
- Needham, Tristan (1997), Visual Complex Analysis , Oxford: Clarendon Press, ISBN 978-0-19-853446-4 (Krásně ilustrovaný úvod do Möbiusových transformací, včetně jejich klasifikace až do konjugace, najdete v kapitole 3.)
- Penrose, Roger ; Rindler, Wolfgang (1984), Spinory a časoprostor, svazek 1: Kalkulus se dvěma spinory a relativistická pole , Cambridge University Press, ISBN 978-0-521-24527-2
- Schwerdtfeger, Hans (1979), Geometrie složitých čísel , Dover, ISBN 978-0-486-63830-0 (Úvod do Möbiusových transformací najdete v kapitole 2.)
- Tóth, Gábor (2002), skupiny konečných Möbiusů, minimální ponoření koulí a modulů
Další čtení
- Lawson, MV (1998). „Inverzní monoid Möbius“ . Journal of Algebra . 200 (2): 428. doi : 10,1006/jabr.1997,7242 .
externí odkazy
-
 Média související s transformací Möbius na Wikimedia Commons
Média související s transformací Möbius na Wikimedia Commons - „Kvazi-konformní mapování“ , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
- Galerie konformních map
- Weisstein, Eric W. „Lineární frakční transformace“ . MathWorld .





































































![{\ Displaystyle [z_ {1}: z_ {2}] \ \ strongsim [z_ {1}/z_ {2}, \ 1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfde0106eeb65683fa6aa517246aab4c2b9360e6)

![{\ Displaystyle [z, \ 1] {\ begin {pmatrix} a & c \\ b & d \ end {pmatrix}} \ = \ [az+b, \ cz+d] \ = \ \ left [{\ frac {az+ b} {cz+d}}, \ 1 \ vpravo] \ = \ f (z).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b8bbc7be964b3996e15687779dfbf71f4c3bdd)