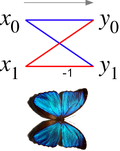Matematický diagram - Mathematical diagram

Euklidovy prvky , ms. z Lüneburgu, 1200 nl

Matematické diagramy , jako jsou grafy a grafy , jsou určeny hlavně k vyjádření matematických vztahů - například k porovnání v čase.

Specifické typy matematických diagramů

Argandův diagram

Argandův diagram.

Komplexní číslo může být vizuálně reprezentován jako dvojice čísel, které tvoří vektor na diagramu nazývaném Argand diagram letadlo komplexu je někdy nazýván argandických rovinu , protože se používá v argandických diagramech . Jsou pojmenovány po Jean-Robertu Argandovi (1768–1822), ačkoli je poprvé popsal norsko-dánský zeměměřič a matematik Caspar Wessel (1745–1818). Argandických diagramy se často používají k vykreslení poloh pólů a nul jednoho funkce v komplexní rovině.

Koncept komplexní roviny umožňuje geometrickou interpretaci komplexních čísel. Pod Kromě toho přidat jako vektorů . Násobení dvou komplexních čísel může být vyjádřena nejsnadněji v polárních souřadnicích - velikost nebo modul produktu je produkt dvou absolutních hodnot , nebo modulů, a úhel nebo tvrzení výrobku je součet obou úhlů, nebo argumenty. Zejména násobení komplexním počtem modulů 1 působí jako rotace.

Motýlí diagram

Motýlí diagram

V kontextu rychlých algoritmů Fourierovy transformace je motýl částí výpočtu, která kombinuje výsledky menších diskrétních Fourierových transformací (DFT) do většího DFT nebo naopak (rozdělení většího DFT na dílčí transformace). Název „motýl“ pochází z tvaru diagramu toku dat v případě radix-2, jak je popsáno níže. Stejnou strukturu lze také najít v algoritmu Viterbi , který se používá k nalezení nejpravděpodobnější sekvence skrytých stavů.

Motýl diagram znázorňují údaje vývojový diagram Připojení vstupů x (vlevo) na výstupy y , které jsou na nich závislé (vpravo) na „butterfly“ krok radix-2 Cooley-Tukey FFT algoritmu . Tento diagram připomíná motýla jako u morpho motýla zobrazeného pro srovnání, odtud název.

Komutativní diagram zobrazující pět lemmat

Komutativní diagram

Hlavní článek: Komutativní diagram

V matematice, a zejména v teorii kategorií , je komutativní diagram diagram objektů , také známý jako vrcholy, a morfismů , také známý jako šipky nebo hrany, takže při výběru dvou objektů vede jakákoli směrovaná cesta skrz diagram ke stejnému výsledku podle složení.

Komutativní diagramy hrají roli v teorii kategorií, kterou rovnice hrají v algebře.

Hasseův diagram.

Hasse diagramy

Hasse schéma je jednoduchý obraz z konečného uspořádaná množina , tvoří výkres částečného objednávky přechodného snížení . Konkrétně jeden představuje každý prvek množiny jako vrchol na stránce a nakreslí úsečku nebo křivku, která jde nahoru z x do y přesně, když x < y a neexistuje žádné z takové, že x < z < y . V tomto případě říkáme, že y pokrývá x, nebo y je bezprostřední nástupce x. V Hasseově diagramu je nutné, aby byly křivky vykresleny tak, aby každá splňovala přesně dva vrcholy: jeho dva koncové body. Jakýkoli takový diagram (vzhledem k tomu, že jsou vrcholy označeny) jednoznačně určuje dílčí řád a jakýkoli dílčí řád má jedinečnou přechodnou redukci, ale existuje mnoho možných umístění prvků v rovině, což má za následek různé Hasseho diagramy pro daný řád, které mohou mají velmi rozdílné vzhledy.

Uzlový diagram.

Uzlové diagramy

V teorii uzlů je užitečným způsobem vizualizace a manipulace s uzly promítnutí uzlu na rovinu - myslete na to, že uzel vrhá stín na zeď. Malá odchylka při výběru projekce zajistí, že bude jedna k jedné, s výjimkou dvojitých bodů zvaných přechody , kde se „stín“ uzlu protíná jednou příčně

Na každém přechodu musíme uvést, který úsek je „přes“ a který „pod“, aby bylo možné znovu vytvořit původní uzel. To se často provádí vytvořením zlomu v prameni, který jde pod ním. Pokud se uzel podle následujícího diagramu střídavě kříží „nad“ a „pod“, pak diagram představuje obzvláště dobře studovanou třídu uzlů, střídavé uzly .

Vennův diagram.

Vennův diagram

Vennův diagram je reprezentace matematických množin: matematické schéma představující sady jako kruhy, s jejich vztahy k sobě vyjádřené prostřednictvím jejich překrývajících se polohách, tak, aby na všechny možné vztahy mezi sadami.

Vennův diagram je sestaven ze sbírky jednoduchých uzavřených křivek nakreslených v rovině. Princip těchto diagramů spočívá v tom, že třídy jsou reprezentovány regiony v takovém vzájemném vztahu, že všechny možné logické vztahy těchto tříd lze označit ve stejném diagramu. To znamená, že diagram zpočátku ponechává prostor pro jakýkoli možný vztah tříd a skutečný nebo daný vztah lze poté určit uvedením, že určitá konkrétní oblast je null nebo není null.

Osy Voronoi.

Voronoiho diagram

Voronoi diagram je zvláštní druh rozkladem metrického prostoru určeném vzdálenostech až do dané diskrétní soubor objektů v prostoru, například tím, že se diskrétní množiny bodů. Tento diagram je pojmenován podle Georgy Voronoi , nazývaného také Voronoiho teselace , Voronoiův rozklad nebo Dirichletova teselace podle Petera Gustava Lejeune Dirichleta .

V nejjednodušším případě dostaneme sadu bodů S v rovině, což jsou místa Voronoi. Každé místo má Voronoiovu buňku V, která se skládá ze všech bodů blíže k s než k jakémukoli jinému místu. Segmenty Voronoiho diagramu jsou všechny body v rovině, které jsou ve stejné vzdálenosti od dvou míst. Uzly Voronoi jsou body ve stejné vzdálenosti od tří (nebo více) míst

Skupinový diagram tapety.

Skupinové diagramy tapet

Skupina tapet nebo skupina rovinné symetrie nebo rovinná krystalografická skupina je matematická klasifikace dvojrozměrného opakujícího se vzoru na základě symetrií ve vzoru. Takové vzory se často vyskytují v architektuře a dekorativním umění. Existuje 17 možných odlišných skupin .

Skupiny tapet jsou dvourozměrné skupiny symetrie , které mají složitost mezi jednoduššími vlysovými skupinami a trojrozměrnými krystalografickými skupinami , nazývanými také vesmírné skupiny . Skupiny tapet kategorizují vzory podle jejich symetrií. Jemné rozdíly mohou umístit podobné vzory do různých skupin, zatímco vzory, které se velmi liší ve stylu, barvě, měřítku nebo orientaci, mohou patřit do stejné skupiny.

Mladý diagram

Young schéma nebo Young tablo , také nazývaný Ferrers schéma , je konečný soubor polí, nebo buněk, uspořádaných do levé zarovnáno řadách, přičemž řada velikostí slabě klesá (každý řádek má stejnou nebo menší délku než jeho předchůdce).

Mladý diagram.

Výpis počtu polí v každém řádku dává rozdělení kladného celého čísla n , celkový počet polí v diagramu. Mladý diagram má tvar a nese stejné informace jako tento oddíl. Uvedením počtu polí v každém sloupci získáte další oddíl, konjugovaný nebo transponovaný oddíl ; jeden získá Youngův diagram tohoto tvaru odrazem původního diagramu podél jeho hlavní úhlopříčky.

Mladá tabla byla představena Alfredem Youngem , matematikem z Cambridgeské univerzity , v roce 1900. Poté byla aplikována na studium symetrické skupiny Georgem Frobeniem v roce 1903. Jejich teorii dále rozvíjelo mnoho matematiků.

Další matematické diagramy

Viz také

Reference

Další čtení

  • Barker-Plummer, Dave; Bailin, Sidney C. (1997). "Role diagramů v matematických důkazech". Strojová grafika a vidění . 6 (1): 25–56. 10.1.1.49.4712 . (Zvláštní vydání o schematickém vyjádření a uvažování).
  • Barker-Plummer, Dave; Bailin, Sidney C. (2001). "K praktické sémantice matematických diagramů". V Anderson, M. (ed.). Odůvodnění se schematickými reprezentacemi . Springer Verlag . ISBN   978-1-85233-242-6 . CiteSeerX : 10.1.1.30.9246 .
  • Kidman, G. (2002). "Přesnost matematických diagramů v učebních osnovách". In Cockburn, A .; Nardi, E. (eds.). Sborník z PME 26 . 3 . University of East Anglia. 201–8.
  • Kulpa, Zenon (2004). "O schematickém znázornění matematických znalostí" . V Andréa Asperti; Bancerek, Grzegorz; Trybulec, Andrzej (eds.). Správa matematických znalostí: třetí mezinárodní konference, MKM 2004, Białowieża, Polsko, 19. – 21. Září 2004: Sborník . Springer. 191–204. ISBN   978-3-540-23029-8 .
  • Puphaiboon, K .; Woodcock, A .; Scrivener, S. (25. března 2005). "Metoda návrhu pro vývoj matematických diagramů". In Bust, Philip D .; McCabe, PT (eds.). Současná ergonomie 2005 Sborník mezinárodní konference o současné ergonomii (CE2005) . Taylor & Francis. ISBN   978-0-415-37448-4 .

externí odkazy