Problém s maximálním průtokem - Maximum flow problem

Síť toku pro problém: Každý člověk (r i ) je ochoten adoptovat kočku (w i 1) a/nebo psa (w i 2). Každý mazlíček (p i ) však dává přednost pouze podskupině lidí. Najděte jakékoli shody domácích mazlíčků s lidmi tak, aby jeden z jejich preferovaných lidí přijal maximální počet domácích zvířat.

V teorii optimalizace , maximální průtok problémy zahrnují najít proveditelný tok přes síť toku , který získá maximální možný průtok.

Problém s maximálním tokem lze považovat za zvláštní případ složitějších problémů s tokem sítě, jako je problém s cirkulací . Maximální hodnota prvního toku (tj. Průtoku ze zdroje s do jímky t) se rovná minimální kapacitě prvního střihu (tj. Přerušení s od t) v síti, jak je uvedeno v min. řezná věta .

Dějiny

Problém maximálního toku poprvé zformulovali v roce 1954 TE Harris a FS Ross jako zjednodušený model toku sovětské železniční dopravy.

V roce 1955 vytvořili Lester R. Ford, Jr. a Delbert R. Fulkerson první známý algoritmus, Ford – Fulkersonův algoritmus . Ford a Fulkerson ve svém příspěvku z roku 1955 napsali, že problém Harrise a Rosse je formulován následovně (viz str. 5):

Zvažte železniční síť spojující dvě města prostřednictvím několika mezilehlých měst, kde je každému spojení sítě přiřazeno číslo představující jeho kapacitu. Za předpokladu ustáleného stavu najděte maximální průtok z jednoho daného města do druhého.

Ve své knize Toky v síti v roce 1962 Ford a Fulkerson napsali:

Autorům to na jaře 1955 položil TE Harris, který ve spojení s generálem FS Rossem (v ret.) Zformuloval zjednodušený model toku železniční dopravy a označil tento konkrétní problém za ústřední problém navržený model [11].

kde [11] odkazuje na tajnou zprávu z roku 1955 Základy metody pro hodnocení kapacit železničních sítí od Harrise a Rosse (viz str. 5).

V průběhu let byla objevena různá vylepšená řešení problému maximálního toku, zejména nejkratší algoritmus rozšiřující cesty Edmonds a Karp a nezávisle Dinitz; algoritmus blokovacího toku Dinitze; push-relabel algoritmus z Goldberg a Tarjan ; a algoritmus binárního blokovacího toku podle Goldberga a Rao. Algoritmy Shermana a Kelnera, Leeho, Orecchie a Sidforda nacházejí přibližně optimální maximální tok, ale fungují pouze v neorientovaných grafech.

V roce 2013 James B. Orlin publikoval článek popisující algoritmus. ${\ displaystyle O (| V || E |)}$

Definice

Proudové sítě, se zdrojovým s a umyvadlem t . Čísla vedle okraje jsou kapacity.

Nejprve vytvoříme nějaký zápis:

• Nechť je síť tím, že je zdrojem, respektive jímačem.${\ displaystyle N = (V, E)}$${\ displaystyle s, t \ in V}$${\ displaystyle N}$
• If je funkce na okrajích pak její hodnota na je označena nebo${\ displaystyle g}$${\ displaystyle N}$${\ Displaystyle (u, v) \ v E}$${\ displaystyle g_ {uv}}$${\ Displaystyle g (u, v).}$

Definice. Kapacita z hrany je maximální množství proudu, který může projít hrany. Formálně jde o mapu${\ Displaystyle c: E \ to \ mathbb {R} ^{+}.}$

Definice. Tok je mapa , která splňuje následující: ${\ Displaystyle f: E \ to \ mathbb {R}}$

• Omezení kapacity . Tok hrany nemůže překročit její kapacitu, jinými slovy: pro všechny${\ Displaystyle f_ {uv} \ leq c_ {uv}}$${\ Displaystyle (u, v) \ v E.}$
• Zachování toků. Součet toků vstupujících do uzlu se musí rovnat součtu toků opouštějících tento uzel, s výjimkou zdroje a jímky. Nebo:

${\ Displaystyle \ forall v \ in V \ setminus \ {s, t \}: \ quad \ sum _ {u: (u, v) \ in E} f_ {uv} = \ sum _ {u: (v, u) \ v E} f_ {vu}.}$

Poznámka . Toky jsou zkosené symetrické: pro všechny${\ Displaystyle f_ {uv} =-f_ {vu}}$${\ Displaystyle (u, v) \ v E.}$

Definice. Hodnota průtoku je množství proudu procházejícího ze zdroje do dřezu. Formálně pro tok je dán: ${\ Displaystyle f: E \ to \ mathbb {R} ^{+}}$

${\ Displaystyle | f | = \ sum _ {v: (s, v) \ in E} f_ {sv}.}$

Definice. Problém maximální průtok je cesta tolik proudu, jak je to možné od zdroje do dřezu, jinými slovy najít tok s maximální hodnotou. ${\ displaystyle f _ {\ textrm {max}}}$

Všimněte si toho, že může existovat několik maximálních toků, a pokud jsou povoleny libovolné skutečné (nebo dokonce libovolné racionální) hodnoty toku (namísto pouze celých čísel), existuje buď přesně jeden maximální tok, nebo nekonečně mnoho, protože existuje nekonečně mnoho lineárních kombinací základní maximální průtoky. Jinými slovy, pokud pošleme jednotky toku na hraně v jednom maximálním toku a jednotky toku dál v jiném maximálním toku, pak pro každý můžeme poslat jednotky a směrovat tok na zbývajících hranách odpovídajícím způsobem, abychom získali další maximální tok. Pokud mohou být hodnoty toku jakákoli reálná nebo racionální čísla, pak takových hodnot existuje nekonečně mnoho pro každý pár . ${\ displaystyle x}$${\ displaystyle u}$${\ displaystyle y> x}$${\ displaystyle u}$${\ Displaystyle \ Delta \ v [0, yx]}$${\ displaystyle x+\ Delta}$${\ displaystyle u}$${\ displaystyle \ Delta}$${\ displaystyle x, y}$

Algoritmy

Následující tabulka uvádí algoritmy pro řešení problému s maximálním tokem.

Metoda	Složitost	Popis
Lineární programování		Omezení daná definicí legálního toku . Podívejte se na lineární program zde.
Algoritmus Ford – Fulkerson	${\ Displaystyle O (E \ vert f_ {max} \ vert)}$	Dokud je přes zbytkový graf otevřená cesta, pošlete na ni minimum zbytkových kapacit. Algoritmus se zaručeně ukončí pouze tehdy, pokud jsou všechny váhy racionální , v takovém případě je množství přidané do toku v každém kroku alespoň největším společným dělitelem vah. Jinak je možné, že se algoritmus nebude sbíhat na maximální hodnotu. Pokud však algoritmus skončí, je zaručeno, že najde maximální hodnotu.
Algoritmus Edmonds – Karp	${\ displaystyle O (VE^{2})}$	Specializace Ford – Fulkerson, hledání rozšiřujících cest s hledáním do šířky .
Dinicův algoritmus	${\ displaystyle O (V^{2} E)}$	V každé fázi algoritmy vytvářejí vrstvený graf s vyhledáváním nejprve na zbytkovém grafu . Maximální průtok ve vrstveném grafu lze vypočítat v čase a maximální počet fází je . V sítích s jednotkovými kapacitami Dinicův algoritmus skončí včas. ${\ displaystyle O (VE)}$${\ displaystyle V-1}$${\ Displaystyle O (\ min \ {V^{2/3}, E^{1/2} \} E)}$
Algoritmus MKM (Malhotra, Kumar, Maheshwari)	${\ displaystyle O (V^{3})}$	Modifikace Dinicova algoritmu s odlišným přístupem ke konstrukci blokovacích toků. Viz originální papír .
Dinicův algoritmus s dynamickými stromy	${\ displaystyle O (VE \ log V)}$	Dynamické stromy datová struktura urychluje výpočtu maximální proudění v vrstvené grafu . ${\ displaystyle O (VE \ log V)}$
Obecný algoritmus push -relabel	${\ displaystyle O (V^{2} E)}$	Algoritmus push relabel udržuje preflow, tj. Funkci toku s možností přebytku ve vrcholech. Algoritmus běží, když je v grafu vrchol s kladným přebytkem, tj. Aktivní vrchol. Operace tlačení zvyšuje průtok na zbytkové hraně a výšková funkce na vrcholech ovládá, přes které lze protlačit zbytkové hrany. Funkce výšky se mění operací relabelu. Správné definice těchto operací zaručují, že výsledná funkce toku je maximální průtok.
Algoritmus push – relabel s pravidlem výběru vrcholů FIFO	${\ displaystyle O (V^{3})}$	Varianta algoritmu push-relabel, která vždy vybere poslední aktivní vrchol, a provádí operace push, zatímco přebytek je kladný a z tohoto vrcholu jsou přípustné zbytkové hrany.
Algoritmus push – relabel s pravidlem výběru vrcholu maximální vzdálenosti	${\ displaystyle O (V^{2} {\ sqrt {E}})}$	Varianta algoritmu push-relabel, která vždy vybere nejvzdálenější vrchol od nebo (tj. Nejvyšší vrchol štítku), ale jinak pokračuje jako algoritmus FIFO. ${\ displaystyle s}$${\ displaystyle t}$
Algoritmus push-relabel s dynamickými stromy	${\ Displaystyle O \ left (VE \ log {\ frac {V^{2}} {E}} \ right)}$	Algoritmus vytváří na zbytkovém grafu stromy omezené velikosti týkající se výškové funkce. Tyto stromy poskytují víceúrovňové operace tlačení, tj. Tlačení po celé saturační dráze místo jediné hrany.
KRT (King, Rao, Tarjan) algoritmus	${\ Displaystyle O \ left (VE \ log _ {\ frac {E} {V \ log V}} V \ right)}$
Algoritmus toku binárního blokování	${\ Displaystyle O \ left (E \ cdot \ min \ {V^{2/3}, E^{1/2} \} \ cdot \ log {\ frac {V^{2}} {E}} \ cdot \ log U \ right)}$	Hodnota U odpovídá maximální kapacitě sítě.
Algoritmus Jamese B Orlina + KRT (King, Rao, Tarjan)	${\ displaystyle O (VE)}$	Orlinův algoritmus řeší maximální průtok v čase, zatímco KRT jej řeší za . ${\ displaystyle O (VE)}$${\ Displaystyle E \ leq O (V^{{\ frac {16} {15}}-\ epsilon})}$${\ displaystyle O (VE)}$${\ Displaystyle E> V^{1+ \ epsilon}}$
Algoritmus Kathuria-Liu-Sidford	${\ Displaystyle E^{4/3+o (1)} U^{1/3}}$	Metody vnitřních bodů a posílení hran pomocí -normových toků. Navazuje na dřívější algoritmus Madry, který dosáhl běhu . ${\ displaystyle \ ell _ {p}}$${\ displaystyle {\ tilde {O}} (E^{10/7} U^{1/7})}$
Algoritmus BLNPSSSW / BLLSSSW	${\ displaystyle {\ tilde {O}} ((E+V^{3/2}) \ log U)}$	Vnitřní bodové metody a dynamická údržba elektrických toků s rozkladem expandéru.
Algoritmus Gao-Liu-Peng	${\ displaystyle {\ tilde {O}} (E^{{\ frac {3} {2}}-{\ frac {1} {328}}} \ log U)}$	Algoritmus Gao, Liu a Penga se točí kolem dynamického udržování rozšiřujících se elektrických toků v jádru algoritmu založeného na metodě vnitřních bodů z [Mądry JACM '16]. To zahrnuje navrhování datových struktur, které v omezeném nastavení vrací hrany s velkou elektrickou energií v grafu procházejícím aktualizacemi odporu.

Další algoritmy viz Goldberg & Tarjan (1988) .

Integrovaná věta o proudění

Uvádí to integrální věta o toku

Pokud má každá hrana v tokové síti integrální kapacitu, pak existuje integrální maximální tok.

Tvrzením je nejen to, že hodnota toku je celé číslo, které vyplývá přímo z věty o minimálním řezu maximálního toku , ale že tok na každé hraně je integrální. To je zásadní pro mnoho kombinatorických aplikací (viz níže), kde tok přes hranu může kódovat, zda položka odpovídající této hraně má být zahrnuta do hledané sady nebo ne.

aplikace

Problém s maximálním průtokem více zdrojů s více jímkami

Obr. 4.1.1. Transformace problému s maximálním průtokem z více zdrojů z více jímek na problém z maximálního toku z jednoho zdroje z jednoho jímače

Vzhledem k síti se sadou zdrojů a sadou propadů namísto pouze jednoho zdroje a jednoho propadu musíme najít maximální průtok napříč . Problém s více zdroji s více jímkami můžeme transformovat na problém s maximálním tokem přidáním konsolidovaného zdroje připojujícího se ke každému vrcholu v a konsolidovaného jímače připojeného každým vrcholem v (také známý jako supersource a supersink ) s nekonečnou kapacitou na každém okraji ( Viz obr. 4.1.1.). ${\ displaystyle N = (V, E)}$${\ Displaystyle S = \ {s_ {1}, \ ldots, s_ {n} \}}$${\ Displaystyle T = \ {t_ {1}, \ ldots, t_ {m} \}}$${\ displaystyle N}$${\ displaystyle S}$${\ displaystyle T}$

Maximální mohutnost bipartitního shody

Obr. 4.3.1. Transformace problému maximálního bipartitního párování na problém maximálního toku

Vzhledem k tomu, bipartitní graf , máme-li najít maximum mohutnost shoda v , že je odpovídající, který obsahuje co největší počet hran. Tento problém lze transformovat na problém maximálního toku vytvořením sítě , kde ${\ Displaystyle G = (X \ cup Y, E)}$${\ displaystyle G}$${\ Displaystyle N = (X \ cup Y \ cup \ {s, t \}, E ')}$

1. ${\ displaystyle E '}$obsahuje hrany směrované od do .${\ displaystyle G}$${\ displaystyle X}$${\ displaystyle Y}$
2. ${\ Displaystyle (s, x) \ in E '}$pro každého a pro každého .${\ displaystyle x \ v X}$${\ Displaystyle (y, t) \ in E '}$${\ displaystyle y \ v Y}$
3. ${\ Displaystyle c (e) = 1}$pro každý (viz obr. 4.3.1).${\ displaystyle e \ in E '}$

Potom se hodnota maximálního průtoku rovná velikosti maximální shody v a maximální shodu mohutnosti lze nalézt tak, že vezmeme ty hrany, které mají průtok v integrálním max. Průtoku. ${\ displaystyle N}$${\ displaystyle G}$${\ displaystyle 1}$

Minimální pokrytí cesty v řízeném acyklickém grafu

Vzhledem k nasměrovanému acyklickému grafu máme najít minimální počet vrcholů-nesouvislých cest, které pokryjí každý vrchol . Můžeme zkonstruovat dvojdílný graf z , kde ${\ displaystyle G = (V, E)}$${\ displaystyle V}$${\ Displaystyle G '= (V _ {\ textrm {out}} \ cup V _ {\ textrm {in}}, E')}$${\ displaystyle G}$

1. ${\ Displaystyle V _ {\ textrm {out}} = \ {v _ {\ textrm {out}} \ mid v \ in V \ land v {\ text {has outgoing edge (s)}} \}}$
2. ${\ Displaystyle V _ {\ textrm {in}} = \ {v _ {\ textrm {in}} \ mid v \ in V \ land v {\ text {has incoming edge (s)}} \}}$
3. ${\ Displaystyle E '= \ {(u _ {\ textrm {out}}, v _ {\ textrm {in}}) \ in V_ {out} \ times V_ {in} \ mid (u, v) \ in E \ }}$.

Pak se může ukázat, že má shodu velikosti právě tehdy, když má vrcholový a nesouvislý kryt cesty obsahující hrany a cesty, kde je počet vrcholů v . Problém lze proto vyřešit tak, že místo toho najdete maximální shodu mohutnosti . ${\ displaystyle G '}$${\ displaystyle M}$${\ displaystyle m}$${\ displaystyle G}$${\ displaystyle C}$${\ displaystyle m}$${\ Displaystyle nm}$${\ displaystyle n}$${\ displaystyle G}$${\ displaystyle G '}$

Intuitivně, pokud jsou dva vrcholy spárovány , pak je hrana obsažena v . Je zřejmé, že počet hran v je . Chcete-li vidět, že je vrchol disjunktní, zvažte následující: ${\ displaystyle u _ {\ mathrm {out}}, v _ {\ mathrm {in}}}$${\ displaystyle M}$${\ displaystyle (u, v)}$${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle m}$${\ displaystyle C}$

1. Každý vrchol v může být buď bez uzavřeno v , v tomto případě nejsou žádné hrany opouští v ; nebo může být uzavřeno , a v tomto případě existuje právě jedna hrana odchází v . V obou případech neopustí žádný vrchol dovnitř více než jeden okraj .${\ displaystyle v _ {\ textrm {out}}}$${\ displaystyle G '}$${\ displaystyle M}$${\ displaystyle v}$${\ displaystyle C}$${\ displaystyle v}$${\ displaystyle C}$${\ displaystyle v}$${\ displaystyle C}$
2. Podobně pro každý vrchol v -, pokud je uzavřeno, je jediná příchozí hranu do oblasti ; jinak nemá žádné příchozí hrany .${\ displaystyle v _ {\ textrm {in}}}$${\ displaystyle G '}$${\ displaystyle v}$${\ displaystyle C}$${\ displaystyle v}$${\ displaystyle C}$

Žádný vrchol tedy nemá dvě příchozí nebo dvě odchozí hrany , což znamená, že všechny cesty v jsou vrcholy-nesouvislé. ${\ displaystyle C}$${\ displaystyle C}$

Abychom ukázali, že kryt má velikost , začneme s prázdným krytem a postupně jej stavíme. Chcete -li přidat vrchol na obálku, můžeme jej buď přidat na existující cestu, nebo vytvořit novou cestu nulové délky začínající na tomto vrcholu. První případ platí vždy, když některá cesta v krytu začíná na , nebo a některá cesta končí na . Druhý případ je vždy použitelný. V prvním případě se celkový počet hran v krytu zvýší o 1 a počet cest zůstane stejný; v druhém případě se počet cest zvýší a počet hran zůstane stejný. Nyní je jasné, že po pokrytí všech vrcholů je součet počtu cest a hran v krytu . Pokud je tedy počet okrajů v krytu , počet cest je . ${\ displaystyle C}$${\ Displaystyle nm}$${\ displaystyle u}$${\ Displaystyle (u, v) \ v E}$${\ displaystyle v}$${\ Displaystyle (v, u) \ v E}$${\ displaystyle v}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle m}$${\ Displaystyle nm}$

Maximální průtok s vrcholovými kapacitami

Obr. 4.4.1. Transformace problému maximálního toku s omezením kapacit vrcholů na původní problém maximálního toku rozdělením uzlů

Budiž síť. Předpokládejme, že v každém uzlu je kromě kapacity na hraně ještě kapacita, tj. Takové mapování , že tok musí splňovat nejen omezení kapacity a zachování toků, ale také omezení kapacity vrcholu ${\ displaystyle N = (V, E)}$${\ Displaystyle c: V \ to \ mathbb {R} ^{+},}$${\ displaystyle f}$

${\ Displaystyle \ sum _ {i \ in V} f_ {iv} \ leq c (v) \ qquad \ forall v \ in V \ zpětné lomítko \ {s, t \}.}$

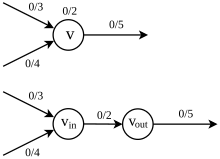
Jinými slovy, množství toku procházející vrcholem nesmí překročit jeho kapacitu. Abychom našli maximální průtok napříč , můžeme problém rozšířit na problém maximálního toku v původním smyslu rozbalením . Nejprve je každý nahrazen a , kde je spojen hranami vstupujícími dovnitř a je spojen s hranami vycházejícími z , pak přiřaďte kapacitu spojování hran a (viz obr. 4.4.1). V této rozšířené síti je omezení kapacity vrcholu odstraněno, a proto lze problém považovat za původní problém maximálního toku. ${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle v \ v V}$${\ displaystyle v _ {\ text {in}}}$${\ displaystyle v _ {\ text {out}}}$${\ displaystyle v _ {\ text {in}}}$${\ displaystyle v}$${\ displaystyle v _ {\ text {out}}}$${\ displaystyle v}$${\ displaystyle c (v)}$${\ displaystyle v _ {\ text {in}}}$${\ displaystyle v _ {\ text {out}}}$

Maximální počet cest od s do t

Vzhledem k usměrněnému grafu a dvěma vrcholům a máme najít maximální počet cest od do . Tento problém má několik variant: ${\ displaystyle G = (V, E)}$${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle s}$${\ displaystyle t}$

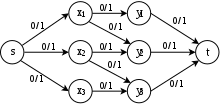
1. Cesty musí být hranaté. Tento problém může být transformována na problém maximálním průtoku vytvořením sítě z , s , a že zdroj a umyvadla v tomto pořadí, a přiřazení každý okraj kapacitu . V této síti je maximální tok, pokud existují cesty oddělující hrany. ${\ displaystyle N = (V, E)}$${\ displaystyle G}$${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle N}$${\ displaystyle 1}$${\ displaystyle k}$${\ displaystyle k}$

2. Cesty musí být nezávislé, tj. Vrchol-nesouvislý (kromě a ). Síť můžeme sestrojit z vertexových kapacit, kde jsou kapacity všech vrcholů a všech hran . Pak se hodnota maximálního průtoku rovná maximálnímu počtu nezávislých cest od do . ${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle N = (V, E)}$${\ displaystyle G}$${\ displaystyle 1}$${\ displaystyle s}$${\ displaystyle t}$

3. Kromě toho, že cesty jsou nesouvislé hrany a/nebo vrcholové, mají cesty také omezení délky: počítáme pouze cesty, jejichž délka je přesně nebo maximálně . Většina variant tohoto problému je NP-úplná, s výjimkou malých hodnot . ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k}$

Problém se zavíráním

Uzávěr z orientovaný graf je sada vrcholů, C , tak, že žádné hrany opustit C . Problém uzavření je úkolem nalezení uzávěru s maximální nebo minimální hmotností v orientovaném grafu váženém na vrchol. Lze to vyřešit v polynomiálním čase pomocí redukce na problém maximálního průtoku.

Aplikace v reálném světě

Vyloučení baseballu

Konstrukce toku sítě pro problém eliminace baseballu

V problému eliminace baseballu soutěží n týmů v lize. V konkrétní fázi ligové sezóny w _i je počet výher a r _i je počet odehraných her pro tým i a r _ij je počet odehraných zápasů proti týmu j . Tým je vyřazen, pokud nemá šanci dokončit sezónu na prvním místě. Úkolem eliminačního problému baseballu je určit, které týmy jsou během sezóny vyřazeny v každém bodě. Schwartz navrhl metodu, která tento problém redukuje na maximální tok sítě. Při této metodě se vytvoří síť, která určí, zda je tým k eliminován.

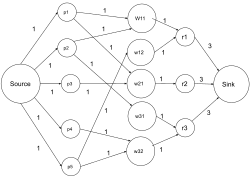
Nechť G = ( V , E ) je síť, kde s , t ∈ V je zdroj a respektive jímka. Jeden přidá herní uzel _ij - který představuje počet her mezi těmito dvěma týmy. Přidáme také týmový uzel pro každý tým a spojíme každý herní uzel { i , j } s i < j do V a každý z nich spojíme od s hranou s kapacitou r _ij - což představuje počet her mezi těmito dvěma týmy. Pro každý tým také přidáme týmový uzel a spojíme každý herní uzel { i , j } se dvěma týmovými uzly i a j, abychom zajistili výhru jednoho z nich. Na těchto hranách není třeba omezovat hodnotu toku. Nakonec jsou vytvořeny hrany z týmového uzlu i do jímacího uzlu t a kapacita w _k + r _k - w _i je nastavena tak, aby zabránil týmu i vyhrát více než w _k + r _k . Nechť S je množina všech týmů účastnících se ligy a nechť

${\ Displaystyle r (S-\ {k \}) = \ sum _ {i, j \ in \ {S-\ {k \} \} \ atop i <j} r_ {ij}}$.

V této metodě se prohlašuje, že tým k není eliminován tehdy a jen tehdy, pokud v síti G existuje hodnota toku velikosti r ( S - { k }) . Ve zmíněném článku je prokázáno, že tato hodnota průtoku je maximální hodnotou průtoku od s do t .

Plánování leteckých společností

V leteckém průmyslu je zásadním problémem plánování letových posádek. Problém s plánováním leteckých společností lze považovat za aplikaci rozšířeného maximálního toku sítě. Vstupem tohoto problému je sada letů F, která obsahuje informace o tom, kde a kdy každý let odlétá a přilétá. V jedné verzi plánování leteckých společností je cílem vytvořit proveditelný plán s maximálně k posádkami.

K vyřešení tohoto problému se používá variace cirkulačního problému nazývaného ohraničený oběh, což je zobecnění problémů s tokem sítě , s přidaným omezením dolní hranice okrajových toků.

Nechť G = ( V , E ) je síť se s , t ∈ V jako uzly zdroje a jímky. Pro zdroj a cíl každého letu i jeden přidá dva uzly do V , uzel s _i jako zdroj a uzel d _i jako cílový uzel letu i . Jeden také přidá do E následující hrany :

1. Okraj s kapacitou [0, 1] mezi s a každým s _i .
2. Okraj s kapacitou [0, 1] mezi každým d _i a t .
3. Okraj s kapacitou [1, 1] mezi každým párem s _i a d _i .
4. Okraj s kapacitou [0, 1] mezi každým d _i a s _j , pokud je zdroj s _j dosažitelný s rozumným množstvím času a nákladů z destinace letu i .
5. Hrana s kapacitou [0, ∞ ] mezi s a t .

Ve zmíněné metodě se tvrdí a prokázalo, že zjištění hodnoty průtoku k v G mezi s a t se rovná nalezení proveditelného plánu pro letovou sadu F s nejvýše k posádkami.

Další verzí plánování leteckých společností je nalezení minimálních potřebných posádek k provedení všech letů. S cílem nalézt odpověď na tento problém, dvojdílný graf G‘ = ( ∪ B , E ), je vytvořen, kde každý let má kopii v souboru A a nastavenou B . V případě, že stejné rovině lze provádět letový j po letu i , i ∈ A je připojen k j ∈ B . Shoda v G ' vyvolá rozvrh pro F a evidentně maximální bipartitní shoda v tomto grafu vytvoří letový řád s minimálním počtem posádek. Jak je uvedeno v části aplikace tohoto článku, je maximální dvoustranná shoda maximální aplikace problémem maximálního toku.

Problém oběhu - poptávka

Existuje několik továren, které vyrábějí zboží, a některé vesnice, kam musí být zboží dodáno. Jsou spojeny sítí silnic, přičemž každá silnice má kapacitu c pro maximální množství zboží, které jí může protékat. Problém je zjistit, zda existuje oběh, který uspokojuje poptávku. Tento problém lze transformovat na problém maximálního toku.

1. Přidejte zdrojový uzel s a přidejte z něj hrany do každého továrního uzlu f _i s kapacitou p _i, kde p _i je rychlost výroby továrního f _i .
2. Přidejte uzel t jímky a přidejte hrany ze všech vesnic v _i až t s kapacitou d _i, kde d _i je míra poptávky vesnice v _i .

Nechť G = ( V , E ) je tato nová síť. Existuje oběh, který uspokojuje poptávku právě tehdy, když:

Maximální hodnota průtoku ( G ) .${\ displaystyle = \ sum _ {i \ in v} d_ {i}}$

Pokud existuje oběh, pohled na řešení maximálního toku by poskytl odpověď na to, kolik zboží musí být odesláno na konkrétní silnici, aby byly uspokojeny požadavky.

Problém lze rozšířit přidáním dolní hranice toku na některých hranách.

Segmentace obrazu

Zdrojový obrázek o velikosti 8x8.

Síť vytvořená z bitmapy. Zdroj je vlevo, umyvadlo vpravo. Čím je hrana tmavší, tím větší je její kapacita. a _i je vysoká, když je pixel zelený, b _i když pixel není zelený. Trest p _ij je stejný.

Kleinberg a Tardos ve své knize představují algoritmus pro segmentaci obrazu. Představují algoritmus k nalezení pozadí a popředí v obrázku. Přesněji řečeno, algoritmus bere bitmapu jako vstup modelovaný následovně: a _i ≥ 0 je pravděpodobnost, že pixel i patří do popředí, b _i ≥ 0 v pravděpodobnosti, že pixel i patří do pozadí, a p _ij je trest, pokud jsou dva sousední pixely i a j umístěny jeden v popředí a druhý v pozadí. Cílem je najít oddíl ( A , B ) sady pixelů, který maximalizuje následující množství

${\ Displaystyle q (A, B) = \ sum _ {i \ in A} a_ {i}+\ sum _ {i \ in B} b_ {i}-\ sum _ {\ begin {matrix} i, j {\ text {vedle}} \\ | A \ cap \ {i, j \} | = 1 \ end {matrix}} p_ {ij}}$,

Skutečně pro pixely v A (považováno za popředí) získáme a _i ; pro všechny pixely v B (považováno za pozadí) získáme b _i . Na hranici mezi dvěma sousedními pixely i a j uvolníme p _ij . Je ekvivalentní minimalizovat množství

${\ Displaystyle q '(A, B) = \ sum _ {i \ in A} b_ {i}+\ sum _ {i \ in B} a_ {i}+\ sum _ {\ begin {matrix} i, j {\ text {soused}} \\ | A \ cap \ {i, j \} | = 1 \ end {matrix}} p_ {ij}}$

protože

${\ Displaystyle q (A, B) = \ sum _ {i \ in A \ cup B} a_ {i}+\ sum _ {i \ in A \ cup B} b_ {i} -q '(A, B ).}$

Minimální řez zobrazený na síti (trojúhelníky VS kruhy).

Nyní vytvoříme síť, jejíž uzly jsou pixely, plus zdroj a jímka, viz obrázek vpravo. Zdroj připojíme k pixelu i o hranu hmotnosti a _i . Pixel i připojíme k jímce hranou závaží b _i . Připojujeme pixel i k pixelu j s hmotností p _ij . Nyní zbývá vypočítat minimální snížení v této síti (nebo ekvivalentně maximální tok). Poslední obrázek ukazuje minimální řez.

Rozšíření

1. V problému toku minimálních nákladů má každá hrana ( u , v) kromě své kapacity také nákladový koeficient a _uv . V případě, že průtok přes hrany f _uv , pak celkové náklady _uv f _uv . Je nutné najít tok dané velikosti d s nejnižšími náklady. Ve většině variant mohou být nákladové koeficienty kladné nebo záporné. Pro tento problém existují různé algoritmy polynomiálního času.

2. Problém maximálního toku může být rozšířen o disjunktivní omezení : negativní disjunktivní omezení říká, že určitý pár hran nemůže současně mít nenulový tok; A pozitivní disjunktivní omezení říká, že v určitém dvojice hran, alespoň jeden musí mít nenulové proudit. S negativními omezeními se problém stává silně NP-tvrdým i pro jednoduché sítě. S pozitivními omezeními je problém polynomický, pokud jsou povoleny frakční toky, ale může být silně NP-tvrdý, když musí být toky integrální.

Reference

Další čtení

• Joseph Cheriyan a Kurt Mehlhorn (1999). „Analýza pravidla výběru nejvyšší úrovně v algoritmu maximálního toku před přetékáním“. Informační dopisy . 69 (5): 239–242. CiteSeerX  10.1.1.42.8563 . doi : 10,1016/S0020-0190 (99) 00019-8 .
• Daniel D. Sleator a Robert E. Tarjan (1983). „Datová struktura pro dynamické stromy“ (PDF) . Journal of Computer and System Sciences . 26 (3): 362–391. doi : 10,1016/0022-0000 (83) 90006-5 . ISSN  0022-0000 .
• Eugene Lawler (2001). „4. Toky v síti“. Kombinatorická optimalizace: Sítě a matroidy . Dover. s. 109–177. ISBN 978-0-486-41453-9.