Minifloat - Minifloat

Formáty s pohyblivou řádovou čárkou
IEEE 754
jiný
Bitové šířky počítačové architektury
Bit
aplikace
Binární přesnost s plovoucí desetinnou čárkou
Desetinná přesnost s plovoucí desetinnou čárkou

V práci na počítači , minifloats jsou plovoucí čárkou hodnoty reprezentovány s velmi málo bitů . Předvídatelně nejsou vhodné pro numerické výpočty pro obecné účely. Používají se pro speciální účely, nejčastěji v počítačové grafice, kde jsou iterace malé a přesnost má estetické efekty. Strojové učení také používá podobné formáty jako bfloat16 . Kromě toho se s nimi často setkáváme jako s pedagogickým nástrojem v kurzech počítačové vědy k demonstraci vlastností a struktur aritmetiky s plovoucí desetinnou čárkou a čísel IEEE 754 .

Minifloaty se 16 bity jsou čísla s poloviční přesností (na rozdíl od jednoduché a dvojité přesnosti ). Existují také minifloaty s 8 bity nebo ještě méně.

Minifloaty lze navrhovat podle zásad standardu IEEE 754 . V tomto případě musí dodržovat (nikoli výslovně napsaná) pravidla pro hranici mezi subnormálními a normálními čísly a musí mít speciální vzory pro nekonečno a NaN . Normalizovaná čísla jsou uložena s předpojatým exponentem . Nová revize standardu IEEE 754-2008 má 16bitové binární minifloaty .

Radeon R300 a R420 GPU používal ve formátu s plovoucí desetinnou čárkou „fp24“ se 7 kousky exponentem a 16 bitů (1) implicitní mantisa. „Full Precision“ v Direct3D 9.0 je patentovaný 24bitový formát s plovoucí desetinnou čárkou. Grafické API Microsoft D3D9 (Shader Model 2.0) zpočátku podporovalo jak FP24 (jako u čipu ATI R300), tak FP32 (jako u čipu NVIDIA NV30) jako „Full Precision“, stejně jako FP16 jako „Partial Precision“ pro výpočty vrcholů a pixel shaderů provádí grafický hardware.

Zápis

Miniploat je obvykle popsán pomocí n -tice čtyř čísel ( S , E , M , B ):

  • S je délka znaménkového pole. Obvykle je to 0 nebo 1.
  • E je délka pole exponentu.
  • M je délka mantisového (významového) pole.
  • B je exponent zaujatost .

Formát miniploatu označený ( S , E , M , B ) je tedy dlouhý S + E + M bitů.

V počítačové grafice se někdy používají miniploty, které představují pouze integrální hodnoty. Pokud by současně měly existovat subnormální hodnoty, musí být nejméně subnormální číslo 1. Hodnota zkreslení by v tomto případě byla B = E - M - 1 za předpokladu, že na IEEE jsou použity dvě speciální exponentní hodnoty.

Zápis ( S , E , M , B ) lze převést na formát ( B , P , L , U ) jako (2, M + 1, B + 1, 2 S - B ) (s použitím IEEE exponentů) .

Příklad

Rozložení příkladu 8bitového minifloatu (1.4.3.-2)
podepsat exponent významný
0 0 0 0 0 0 0 0

V tomto příkladu se pro reprezentaci integrálních hodnot používá minifloat v 1 bajtu (8 bitů) s 1 znaménkovým bitem, 4 exponentními bity a 3 významnými bity (zkrátka 1.4.3. -2 minifloat). Všechny zásady IEEE 754 by měly být platné. Jedinou volnou hodnotou je zkreslení exponentu , které definujeme jako -2 pro celá čísla. Neznámý exponent je volán pro okamžik x .

Čísla v jiné základně jsou označena jako ... základna , například 101 2 = 5. Bitové vzory mají mezery pro vizualizaci svých částí.

Reprezentace nuly

0 0000 000 = 0

Podnormální čísla

Význam je rozšířen o „0“: 

0 0000 001 = 0.0012 × 2x = 0.125 × 2x = 1 (least subnormal number)
...
0 0000 111 = 0.1112 × 2x = 0.875 × 2x = 7 (greatest subnormal number)

Normalizovaná čísla

Význam je rozšířen o „1.“: 

0 0001 000 = 1.0002 × 2x = 1 × 2x = 8 (least normalized number)
0 0001 001 = 1.0012 × 2x = 1.125 × 2x = 9
...
0 0010 000 = 1.0002 × 2x+1 = 1 × 2x+1 = 16
0 0010 001 = 1.0012 × 2x+1 = 1.125 × 2x+1 = 18
...
0 1110 000 = 1.0002 × 2x+13 =  1.000 × 2x+13 =  65536
0 1110 001 = 1.0012 × 2x+13 =  1.125 × 2x+13 =  73728
...
0 1110 110 = 1.1102 × 2x+13 =  1.750 × 2x+13 = 114688
0 1110 111 = 1.1112 × 2x+13 =  1.875 × 2x+13 = 122880 (greatest normalized number)

Nekonečno

0 1111 000 = +infinity
1 1111 000 = −infinity

Pokud by pole exponent nebylo zpracováno speciálně, hodnota by byla 

0 1111 000 = 1.0002 × 2x+14 =  217 = 131072

Ne číslo

x 1111 yyy = NaN (if yyy ≠ 000)

Bez zvláštního zacházení s největším exponentem IEEE 754 by byla největší možná hodnota 

0 1111 111 = 1.1112 × 2x+14 =  1.875 × 217 = 245760

Hodnota předpětí

Pokud má být nejméně subnormální hodnota (druhý řádek výše) 1, hodnota x musí být x = 3. Zkreslení tedy musí být −2; to znamená, že každý uložený exponent musí být snížen o −2 nebo musí být zvýšen o 2, aby se získal numerický exponent.

Všechny hodnoty jako desetinná místa

Toto je graf všech možných hodnot při zacházení s plovákem podobně jako s plovákem IEEE.

... 000 ... 001 ... 010 ... 011 ... 100 ... 101 ... 110 ... 111
0 0000 ... 0 0,125 0,25 0,375 0,5 0,625 0,75 0,875
0 0001 ... 1 1,125 1,25 1,375 1.5 1,625 1,75 1,875
0 0010 ... 2 2.25 2.5 2,75 3 3,25 3.5 3,75
0 0011 ... 4 4.5 5 5.5 6 6.5 7 7.5
0 0100 ... 8 9 10 11 12 13 14 15
0 0101 ... 16 18 20 22 24 26 28 30
0 0110 ... 32 36 40 44 48 52 56 60
0 0111 ... 64 72 80 88 96 104 112 120
0 1000 ... 128 144 160 176 192 208 224 240
0 1001 ... 256 288 320 352 384 416 448 480
0 1010 ... 512 576 640 704 768 832 896 960
0 1011 ... 1024 1152 1280 1408 1536 1664 1792 1920
0 1100 ... 2048 2304 2560 2816 3072 3328 3584 3840
0 1101 ... 4096 4608 5120 5632 6144 6656 7168 7680
0 1110 ... 8192 9216 10240 11264 12288 13312 14336 15360
0 1111 ... Inf NaN NaN NaN NaN NaN NaN NaN
1 0000 ... -0 -0,125 -0,25 -0,375 -0,5 -0,625 -0,75 -0,875
1 0001 ... -1 -1,125 -1,25 -1,375 -1,5 -1,625 -1,75 -1,875
1 0010 ... -2 -2,25 -2,5 -2,75 -3 -3,25 -3,5 -3,75
1 0011 ... -4 -4,5 -5 -5,5 -6 -6,5 -7 -7,5
1 0100 ... −8 −9 −10 −11 −12 −13 −14 −15
1 0101 ... −16 −18 −20 −22 −24 −26 −28 −30
1 0110 ... −32 −36 −40 -44 -48 −52 -56 −60
1 0111 ... −64 -72 -80 -88 -96 −104 −112 -120
1 1000 ... −128 −144 -160 −176 −192 -208 −224 -240
1 1001 ... −256 −288 −320 -352 −384 -416 −448 -480
1 1010 ... -512 -576 −640 -704 −768 −832 −896 -960
1 1011 ... −1024 −1152 −1280 -1408 −1536 −1664 −1792 −1920
1 1100 ... -2048 -2304 −2560 −2816 -3072 −3328 -3584 −3840
1 1101 ... -4096 -4608 −5120 -5632 -6144 -6656 -7168 -7680
1 1110 ... −8192 −9216 −10240 −11264 −12288 −13312 −14336 −15360
1 1111 ... - Inf NaN NaN NaN NaN NaN NaN NaN

Všechny hodnoty jako celá čísla

Kvůli závažnému nedostatku přesnosti u 8bitových plováků se doporučuje používat je pouze v měřítku na celočíselné hodnoty.

... 000 ... 001 ... 010 ... 011 ... 100 ... 101 ... 110 ... 111
0 0000 ... 0 1 2 3 4 5 6 7
0 0001 ... 8 9 10 11 12 13 14 15
0 0010 ... 16 18 20 22 24 26 28 30
0 0011 ... 32 36 40 44 48 52 56 60
0 0100 ... 64 72 80 88 96 104 112 120
0 0101 ... 128 144 160 176 192 208 224 240
0 0110 ... 256 288 320 352 384 416 448 480
0 0111 ... 512 576 640 704 768 832 896 960
0 1000 ... 1024 1152 1280 1408 1536 1664 1792 1920
0 1001 ... 2048 2304 2560 2816 3072 3328 3584 3840
0 1010 ... 4096 4608 5120 5632 6144 6656 7168 7680
0 1011 ... 8192 9216 10240 11264 12288 13312 14336 15360
0 1100 ... 16384 18432 20480 22528 24576 26624 28672 30720
0 1101 ... 32768 36864 40960 45056 49152 53248 57344 61440
0 1110 ... 65536 73728 81920 90112 98304 106496 114688 122880
0 1111 ... Inf NaN NaN NaN NaN NaN NaN NaN
1 0000 ... −0 -1 −2 −3 −4 −5 −6 −7
1 0001 ... −8 −9 −10 −11 −12 −13 −14 −15
1 0010 ... −16 −18 −20 −22 −24 −26 −28 −30
1 0011 ... −32 −36 −40 -44 -48 −52 -56 −60
1 0100 ... −64 -72 -80 -88 -96 −104 −112 -120
1 0101 ... −128 −144 -160 −176 −192 -208 −224 -240
1 0110 ... −256 −288 −320 -352 −384 -416 −448 -480
1 0111 ... -512 -576 −640 -704 −768 −832 −896 -960
1 1000 ... −1024 −1152 −1280 -1408 −1536 −1664 −1792 −1920
1 1001 ... -2048 -2304 −2560 −2816 -3072 −3328 -3584 −3840
1 1010 ... -4096 -4608 −5120 -5632 -6144 -6656 -7168 -7680
1 1011 ... −8192 −9216 −10240 −11264 −12288 −13312 −14336 −15360
1 1100 ... −16384 −18432 −20480 −22528 −24576 −26624 −28672 −30720
1 1101 ... −32768 −36864 −40960 −45056 -49152 -53248 -57344 −61440
1 1110 ... −65536 −73728 −81920 −90112 -98304 −106496 −114688 −122880
1 1111 ... - Inf NaN NaN NaN NaN NaN NaN NaN

V praxi se však plováky nezobrazují přesně. Místo toho jsou zaoblené; pokud by například plovák měl přibližně 3 platné číslice a bylo by zobrazeno číslo 8192, bylo by zaokrouhleno na 8190, aby se zabránilo falešné přesnosti , jinak by bylo číslo jako 10 000 000 převedeno na takový plovák a zpět matoucím způsobem zobrazeno jako např. , 1000448.

Vlastnosti tohoto příkladu

Grafické znázornění integrálních (1.4.3. -2) minifloatů

Integrované minifloaty v 1 bajtu mají větší rozsah ± 122 880 než celé číslo s dvojitým komplementem s rozsahem −128 až +127. Větší rozsah je kompenzován špatnou přesností, protože existují pouze 4 bity mantisy, což je o něco více než jedno desetinné místo. Mají také větší dosah než miniploty s poloviční přesností s rozsahem ± 65 504, což je také kompenzováno nedostatkem zlomků a špatnou přesností.

Existuje pouze 242 různých hodnot (pokud jsou +0 a -0 považovány za různé), protože 14 bitových vzorů představuje NaN.

Hodnoty mezi 0 a 16 mají stejný bitový vzor jako minifloat nebo celé číslo s dvojitým komplementem. První vzor s jinou hodnotou je 00010001, což je 18 jako minifloat a 17 jako celé číslo s dvojitým doplňkem.

K této shodě u záporných hodnot vůbec nedochází, protože tento minifloat je formát se znaménkem.

(Svislá) skutečná čára vpravo jasně ukazuje proměnlivou hustotu hodnot s plovoucí desetinnou čárkou-vlastnost, která je společná každému systému s plovoucí desetinnou čárkou. Tato proměnlivá hustota má za následek křivku podobnou exponenciální funkci.

Ačkoli se křivka může zdát hladká, není tomu tak. Graf se ve skutečnosti skládá z odlišných bodů a tyto body leží na úsečkách s diskrétními svahy. Hodnota exponentních bitů určuje absolutní přesnost bitů mantisy a právě tato přesnost určuje sklon každého lineárního segmentu.

Aritmetický

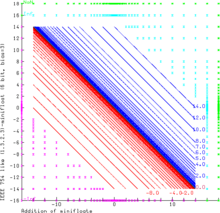
Přidání

Přidání (1.3.2.3) -minifloatů

Grafika ukazuje přidání ještě menších (1.3.2.3) -minifloatů se 6 bity. Tento systém s plovoucí desetinnou čárkou přesně dodržuje pravidla IEEE 754. NaN jako operand produkuje vždy výsledky NaN. Inf - Inf a (−Inf) + Inf má za následek také NaN (zelená plocha). Inf lze beze změny zvětšit a zmenšit o konečné hodnoty. Součty s konečnými operandy mohou dát nekonečný výsledek (tj. 14,0 + 3,0 = + Inf v důsledku toho je azurová oblast, −Inf je purpurová oblast). Rozsah konečných operandů je vyplněn křivkami x + y = c , kde c je vždy jedna z reprezentativních pohyblivých hodnot (modrá a červená pro kladné a záporné výsledky).

Odčítání, násobení a dělení

Ostatní aritmetické operace lze znázornit podobně:

  • Odčítání

  • Násobení

  • Divize

Ve vestavěných zařízeních

Minifloaty se také běžně používají ve vestavěných zařízeních, zejména na mikrokontrolérech, kde bude třeba softwarově emulovat plovoucí desetinnou čárku. Aby se výpočet zrychlil, mantisa obvykle zabírá přesně polovinu bitů, takže hranice registru automaticky adresuje části bez posunu.

Viz také

Reference

  1. ^ Buck, Ian (13. března 2005), „Kapitola 32. Ponoření do GPU Computing“ , v Pharr, Matt (ed.), GPU Gems , ISBN 0-321-33559-7, vyvolány 5. dubna 2018.

Další čtení

externí odkazy