Multidimenzionální diskrétní konvoluce - Multidimensional discrete convolution

Při zpracování signálu se vícedimenzionální diskrétní konvoluce týká matematické operace mezi dvěma funkcemi f a g na n -dimenzionální mřížce, která produkuje třetí funkci, také n -rozměrů. Multidimenzionální diskrétní konvoluce je diskrétní analog vícedimenzionální konvoluce funkcí v euklidovském prostoru. Je to také speciální případ konvoluce na skupiny, když skupina je skupina n -tuples celých čísel.

Definice

Prohlášení o problému a základy

Podobně jako v jednorozměrném případě je pro reprezentaci konvoluční operace použita hvězdička. Počet rozměrů v dané operaci se odráží v počtu hvězdiček. Například M -dimenzionální konvoluce by byla napsána s M hvězdičkami. Následující text představuje M -dimenzionální konvoluci diskrétních signálů:

${\ Displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}, n_ {2}, ..., n_ {M})*{\ přesah {M} {\ cdots}}*h (n_ {1}, n_ {2}, ..., n_ {M})}$

U signálů s diskrétní hodnotou lze tuto konvoluci vypočítat přímo pomocí následujícího:

${\ Displaystyle \ sum _ {k_ {1} =-\ infty}^{\ infty} \ sum _ {k_ {2} =-\ infty}^{\ infty} ... \ sum _ {k_ {M} =-\ infty}^{\ infty} h (k_ ​​{1}, k_ {2}, ..., k_ {M}) x (n_ {1} -k_ {1}, n_ {2} -k_ { 2}, ..., n_ {M} -k_ {M})}$

Výsledná výstupní oblast podpory diskrétní vícerozměrné konvoluce bude určena na základě velikosti a oblastí podpory dvou vstupních signálů.

Uvedeno je několik vlastností dvojrozměrného konvolučního operátoru. Všimněte si, že tyto mohou být také rozšířeny o signály -dimenze. ${\ displaystyle N}$

Komutativní majetek:

${\ Displaystyle x ** h = h ** x}$

Přidružená nemovitost:

${\ Displaystyle (x ** h) ** g = x ** (h ** g)}$

Distribuční vlastnictví:

${\ Displaystyle x ** (h+g) = (x ** h)+(x ** g)}$

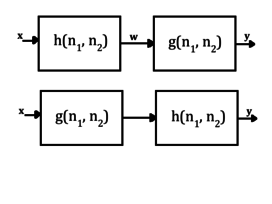
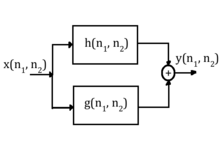
Tyto vlastnosti jsou vidět při použití na obrázku níže. Vzhledem k nějakému vstupu, který jde do filtru s impulsní odezvou a pak do jiného filtru s impulzní odezvou , je výstup dán . Předpokládejme, že výstup prvního filtru je dán , to znamená, že: ${\ displaystyle x (n_ {1}, n_ {2})}$${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle g (n_ {1}, n_ {2})}$${\ displaystyle y (n_ {1}, n_ {2})}$${\ Displaystyle w (n_ {1}, n_ {2})}$

${\ Displaystyle w = x ** h}$

Dále je tato mezilehlá funkce konvolvována s impulzní odezvou druhého filtru, a proto může být výstup reprezentován:

${\ Displaystyle y = w ** g = (x ** h) ** g}$

Pomocí asociativní vlastnosti to lze přepsat následujícím způsobem:

${\ Displaystyle y = x ** (h ** g)}$

což znamená, že ekvivalentní impulsní odezva pro kaskádovaný systém je dána vztahem:

${\ displaystyle h_ {eq} = h ** g}$

Podobnou analýzu lze provést na sadě paralelních systémů znázorněných níže.

V tomto případě je jasné, že:

${\ Displaystyle y = (x ** h)+(x ** g)}$

Pomocí distribučního zákona se ukazuje, že:

${\ Displaystyle y = x ** (h+g)}$

To znamená, že v případě paralelního systému je ekvivalentní impulzní odezva zajištěna:

${\ displaystyle h_ {eq} = h+g}$

Ekvivalentní impulzní odezvy v kaskádových i paralelních systémech lze zobecnit na systémy s počtem filtrů. ${\ displaystyle N}$

Motivace a aplikace

Konvoluce v jedné dimenzi byla silným objevem, který umožnil snadné porovnávání vstupu a výstupu systému s lineárním posunem invariantního (LSI) (viz teorie systému LTI ), pokud byla známa impulzní odezva filtračního systému. Tato představa se přenáší i do vícerozměrné konvoluce, protože pouhá znalost impulsní odezvy vícerozměrného filtru také umožňuje přímé srovnání mezi vstupem a výstupem systému. To je hluboké, protože několik signálů, které jsou dnes přenášeny v digitálním světě, má více dimenzí, včetně obrázků a videí. Podobně jako u jednorozměrné konvoluce umožňuje vícedimenzionální konvoluce výpočet výstupu systému LSI pro daný vstupní signál.

Zvažte například obrázek, který je odeslán přes některou bezdrátovou síť vystavenou elektrooptickému šumu. Mezi možné zdroje šumu patří chyby v přenosu kanálu, převodník analogového signálu na digitální a obrazový snímač. Hluk způsobený kanálem nebo senzorem obvykle vytváří prostorově nezávislé vysokofrekvenční složky signálu, které se promítají do libovolných světlých a tmavých skvrn na skutečném obrazu. Aby se obrazová data zbavila vysokofrekvenčního spektrálního obsahu, lze je znásobit frekvenční charakteristikou dolního propustného filtru, který na základě konvoluční věty odpovídá svinutí signálu v časové/prostorové doméně impulzní odezva dolní propusti. Níže je uvedeno několik impulsních reakcí, které tak činí.

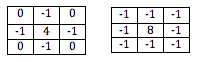
Kromě odfiltrování spektrálního obsahu může vícedimenzionální konvoluce implementovat detekci hran a vyhlazování. To je opět zcela závislé na hodnotách impulzní odezvy, která se používá ke konvoluci se vstupním obrazem. Typické impulzní reakce pro detekci hran jsou znázorněny níže.

Kromě zpracování obrazu lze implementovat vícerozměrnou konvoluci, která umožňuje řadu dalších aplikací. Protože jsou filtry v digitálních komunikačních systémech rozšířené, jakýkoli systém, který musí přenášet vícerozměrná data, je podporován technikami filtrování. Používá se při zpracování videa v reálném čase, analýze neuronových sítí, digitální geofyzikální analýze dat a mnoha dalších.

Jedním z typických zkreslení, ke kterým dochází při pořizování nebo přenosu obrázků a videa, je rozostření způsobené nízkoprůchodovým filtračním procesem. Uvedené rozostření lze modelovat pomocí Gaussova dolnoprůchodového filtrování.

Rozklad řádek-sloupec s oddělitelnými signály

Oddělitelné signály

Říká se, že signál je oddělitelný, pokud jej lze zapsat jako součin více jednorozměrných signálů. Matematicky je to vyjádřeno následovně:

${\ Displaystyle x (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}) x (n_ {2}) ... x (n_ {M})}$

Některé snadno rozpoznatelné oddělitelné signály zahrnují funkci jednotkového kroku a impulsní funkci dirac-delta.

${\ Displaystyle u (n_ {1}, n_ {2}, ..., n_ {M}) = u (n_ {1}) u (n_ {2}) ... u (n_ {M})}$ (funkce krokování)

${\ Displaystyle \ delta (n_ {1}, n_ {2}, ..., n_ {M}) = \ delta (n_ {1}) \ delta (n_ {2}) ... \ delta (n_ { M})}$ (impulsní funkce dirac-delta)

Konvoluce je lineární operace. Z toho pak vyplývá, že vícerozměrná konvoluce oddělitelných signálů může být vyjádřena jako součin mnoha jednorozměrných konvolucí. Zvažte například případ, kdy x a h jsou obě oddělitelné funkce.

${\ Displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = \ sum _ {k_ {1} =-\ infty}^{\ infty} \ sum _ {k_ {2} =-\ infty}^{\ infty} h (k_ ​​{1}, k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) }$

Aplikováním vlastností oddělitelnosti to pak lze přepsat jako následující:

${\ Displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = {\ bigg (} \ sum _ {k_ {1} =-\ infty}^{ \ infty} h (k_ ​​{1}) x (n_ {1} -k_ {1}) {\ bigg)} {\ bigg (} \ sum _ {k_ {2} =-\ infty}^{\ infty} h (k_ ​​{2}) x (n_ {2} -k_ {2}) {\ bigg)}}$

Pak je snadno vidět, že se to redukuje na součin jednorozměrných konvolucí:

${\ Displaystyle x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2}) = {\ bigg [} x (n_ {1})*h (n_ {1}) {\ bigg]} {\ bigg [} x (n_ {2})*h (n_ {2}) {\ bigg]}}$

Tento závěr lze poté rozšířit na konvoluci dvou oddělitelných M -dimenzionálních signálů následujícím způsobem:

${\ Displaystyle x (n_ {1}, n_ {2}, ..., n_ {M})*{\ overset {M} {\ cdots}}*h (n_ {1}, n_ {2} ,. .., n_ {M}) = {\ bigg [} x (n_ {1})*h (n_ {1}) {\ bigg]} {\ bigg [} x (n_ {2})*h (n_ {2}) {\ bigg]} ... {\ bigg [} x (n_ {M})*h (n_ {M}) {\ bigg]}}$

Když jsou tedy dva signály oddělitelné, vícedimenzionální konvoluci lze vypočítat výpočtem jednorozměrných konvolucí. ${\ displaystyle n_ {M}}$

Rozklad sloupců a řádků

Metodu řádek-sloupec lze použít, když je jeden ze signálů v konvoluci oddělitelný. Tato metoda využívá vlastnosti oddělitelnosti, aby dosáhla metody výpočtu konvoluce dvou vícerozměrných signálů, která je výpočetně efektivnější než přímé počítání každého vzorku (vzhledem k tomu, že jeden ze signálů je oddělitelný). Následující text ukazuje matematické zdůvodnění přístupu k rozkladu řádků a sloupců (obvykle jde o oddělitelný signál): ${\ displaystyle h (n_ {1}, n_ {2})}$

${\ Displaystyle {\ begin {aligned} y (n_ {1}, n_ {2}) & = \ sum _ {k_ {1} =-\ infty}^{\ infty} \ sum _ {k_ {2} = -\ infty}^{\ infty} h (k_ ​​{1}, k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) \\ & = \ sum _ {k_ {1} =-\ infty}^{\ infty} \ sum _ {k_ {2} =-\ infty}^{\ infty} h_ {1} (k_ {1}) h_ {2} (k_ { 2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) \\ & = \ sum _ {k_ {1} =-\ infty}^{\ infty} h_ {1 } (k_ {1}) {\ Bigg [} \ sum _ {k_ {2} =-\ infty}^{\ infty} h_ {2} (k_ {2}) x (n_ {1} -k_ {1 }, n_ {2} -k_ {2}) {\ Bigg]} \ end {zarovnáno}}}$

Hodnotu hodnoty lze nyní znovu použít při vyhodnocování jiných hodnot se sdílenou hodnotou : ${\ Displaystyle \ sum _ {k_ {2} =-\ infty}^{\ infty} h_ {2} (k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ { 2})}$${\ displaystyle y}$${\ displaystyle n_ {2}}$

${\ Displaystyle {\ begin {aligned} y (n_ {1}+\ delta, n_ {2}) & = \ sum _ {k_ {1} =-\ infty}^{\ infty} h_ {1} (k_ {1}) {\ Bigg [} \ sum _ {k_ {2} =-\ infty}^{\ infty} h_ {2} (k_ {2}) x (n_ {1}-[k_ {1}- \ delta], n_ {2} -k_ {2}) {\ Bigg]} \\ & = \ sum _ {k_ {1} =-\ infty}^{\ infty} h_ {1} (k_ {1} +\ delta) {\ Bigg [} \ sum _ {k_ {2} =-\ infty}^{\ infty} h_ {2} (k_ {2}) x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) {\ Bigg]} \ end {aligned}}}$

Výslednou konvoluci lze tedy efektivně vypočítat tak, že se nejprve provede operace konvoluce na všech řádcích a poté na všech jejích sloupcích. Tento přístup lze dále optimalizovat s přihlédnutím k tomu, jak je k paměti přistupováno v počítačovém procesoru. ${\ displaystyle x (n_ {1}, n_ {2})}$

Procesor načte data signálu potřebná pro danou operaci. U moderních procesorů se data načtou z paměti do mezipaměti procesorů, která má rychlejší přístupové časy než paměť. Samotná mezipaměť je rozdělena na řádky. Při načítání řádku mezipaměti z paměti se načte více datových operandů najednou. Zvažte optimalizovaný případ, kdy se řada dat signálu zcela vejde do mezipaměti procesoru. Tento konkrétní procesor by byl schopen efektivně přistupovat k datům po řádcích, ale ne po sloupcích, protože různé datové operandy ve stejném sloupci by ležely na různých řádcích mezipaměti. Aby bylo možné využít způsob přístupu k paměti, je efektivnější transponovat datovou sadu a poté ji osově řadit, než se k ní pokoušet přistupovat po sloupcích. Algoritmus se pak stane:

1. Rozdělte oddělitelný dvojrozměrný signál na dva jednorozměrné signály a${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle h_ {1} (n_ {1})}$${\ displaystyle h_ {2} (n_ {2})}$
2. Proveďte řádkovou konvoluci na horizontálních složkách signálu pomocí k získání${\ displaystyle x (n_ {1}, n_ {2})}$${\ displaystyle h_ {1} (n_ {1})}$${\ displaystyle g (n_ {1}, n_ {2})}$
3. Transponujte svislé složky signálu vyplývající z kroku 2.${\ displaystyle g (n_ {1}, n_ {2})}$
4. Proveďte řádkovou konvoluci na transponovaných vertikálních komponentách, abyste získali požadovaný výstup${\ displaystyle g (n_ {1}, n_ {2})}$${\ displaystyle y (n_ {1}, n_ {2})}$

Výpočetní zrychlení z rozkladu sloupců řádků

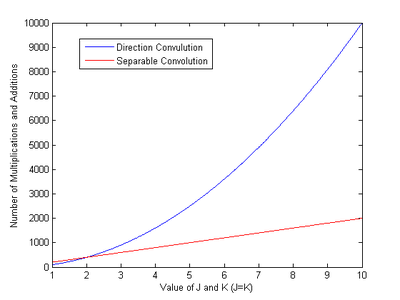
Prohlédněte si případ, kdy je obrázek velikosti procházen oddělitelným filtrem velikosti . Samotný obrázek nelze oddělit. Pokud je výsledek vypočítán pomocí přímého konvolučního přístupu bez využití oddělitelnosti filtru, bude to vyžadovat přibližně násobení a sčítání. Pokud vezmeme v úvahu oddělitelnost filtru, lze filtrování provést ve dvou krocích. První krok bude mít násobení a sčítání a druhý krok bude mít za následek celkem nebo násobení a sčítání. Porovnání výpočetní složitosti mezi přímou a oddělitelnou konvolucí je uvedeno na následujícím obrázku: ${\ displaystyle X \ times Y}$${\ displaystyle J \ times K}$${\ displaystyle XYJK}$${\ displaystyle XYJ}$${\ displaystyle XYK}$${\ displaystyle XYJ+XYK}$${\ displaystyle XY (J+K)}$

Kruhová konvoluce vícerozměrných signálů s diskrétní hodnotou

Předpokladem přístupu kruhové konvoluce u vícerozměrných signálů je vyvinout vztah mezi konvoluční větou a diskrétní Fourierovou transformací (DFT), který lze použít k výpočtu konvoluce mezi dvěma signály s diskrétní hodnotou konečného rozsahu.

Konvoluční věta ve více dimenzích

U jednorozměrných signálů Konvoluční věta uvádí, že Fourierova transformace konvoluce mezi dvěma signály se rovná součinu Fourierových transformací těchto dvou signálů. Konvoluce v časové oblasti se tedy rovná násobení ve frekvenční oblasti. Matematicky je tento princip vyjádřen následujícím způsobem:

Tento princip je přímo rozšiřitelný na řešení signálů více dimenzí.Tato vlastnost je snadno rozšířena na použití s diskrétní Fourierovou transformací (DFT) následovně (všimněte si, že lineární konvoluce je nahrazena kruhovou konvolucí, kde se používá k označení operace kruhové konvoluce velikosti ): ${\ Displaystyle \ otimes}$${\ displaystyle N}$

${\ Displaystyle y (n) = h (n) \ otimes x (n) \ longleftrightarrow Y (k) = H (k) X (k)}$

Při řešení signálů více dimenzí:

Kruhové závity zde budou mít velikost . ${\ displaystyle N_ {1}, N_ {2}, ..., N_ {M}}$

Kruhový konvoluční přístup

Motivací použití přístupu s kruhovou konvolucí je, že je založen na DFT. Předpokladem kruhové konvoluce je vzít DFT vstupních signálů, vynásobit je dohromady a poté vzít inverzní DFT. Je třeba dbát na to, aby byl použit dostatečně velký DFT, aby nedošlo k aliasingu. Při zpracování signálů konečného rozsahu je DFT numericky vypočítatelný. Jednou výhodou tohoto přístupu je, že jelikož vyžaduje převzetí DFT a inverzního DFT, je možné využít efektivní algoritmy, jako je Fast Fourierova transformace (FFT). Kruhovou konvoluci lze také vypočítat v časové/prostorové doméně a nejen ve frekvenční oblasti.

Výběrem velikosti DFT se vyhnete aliasingu

Uvažujme následující případ, kdy jsou brány dva signály konečného rozsahu x a h . Pro oba signály existuje odpovídající DFT následovně:

${\ Displaystyle x (n_ {1}, n_ {2}) \ longleftrightarrow X (k_ {1}, k_ {2})}$ a ${\ Displaystyle h (n_ {1}, n_ {2}) \ longleftrightarrow H (k_ {1}, k_ {2})}$

Region podpory je a region podpory je a . ${\ displaystyle x (n_ {1}, n_ {2})}$${\ Displaystyle 0 \ leq n_ {1} \ leq P_ {1} -1}$${\ Displaystyle 0 \ leq n_ {2} \ leq P_ {2} -1}$${\ displaystyle h (n_ {1}, n_ {2})}$${\ Displaystyle 0 \ leq n_ {1} \ leq Q_ {1} -1}$${\ Displaystyle 0 \ leq n_ {2} \ leq Q_ {2} -1}$

Lineární konvoluce těchto dvou signálů by byla dána jako:

Vzhledem k regionům podpory a bude region podpory poté uveden jako následující: ${\ displaystyle x (n_ {1}, n_ {2})}$${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle y_ {linear} (n_ {1}, n_ {2})}$

Na základě oblastí podpory těchto dvou signálů musí být použit DFT velikosti, kde a protože na obou signálech musí být použit DFT stejné velikosti. V případě, že je potřeba velikost DFT větší než rozsah signálu, je signál nulován, dokud nedosáhne požadované délky. Po vynásobení DFT a převzetí inverzního DFT na výsledek je výsledná kruhová konvoluce dána vztahem: ${\ displaystyle N_ {1} \ times N_ {2}}$${\ displaystyle N_ {1} \ geq \ max (P_ {1}, Q_ {1})}$${\ displaystyle N_ {2} \ geq \ max (P_ {2}, Q_ {2})}$

${\ Displaystyle y_ {circle} (n_ {1}, n_ {2}) = \ sum _ {r_ {1}} \ sum _ {r_ {2}} {\ Bigg [} \ sum _ {m_ {1} = 0}^{Q_ {1} -1} \ sum _ {m_ {2} = 0}^{Q_ {2} -1} h (m_ {1}, m_ {2}) x (n_ {1} -m_ {1} -r_ {1} N_ {1}, n_ {2} -m_ {2} -r_ {2} N_ {2}) {\ Bigg]}}$ pro ${\ Displaystyle (n_ {1}, n_ {2}) \ v R_ ​​{N_ {1} N_ {2}}}$

${\ Displaystyle R_ {N_ {1} N_ {2}} \ triangleq \ {(n_ {1}, n_ {2}): 0 \ leq n_ {1} \ leq N_ {1} -1,0 \ leq n_ {2} \ leq N_ {2} -1 \}}$

Výsledkem bude, že to bude prostorově aliasovaná verze výsledku lineární konvoluce . To lze vyjádřit následovně: ${\ displaystyle y_ {kruh} (n_ {1}, n_ {2})}$${\ displaystyle y_ {linear} (n_ {1}, n_ {2})}$

${\ Displaystyle y_ {circle} (n_ {1}, n_ {2}) = \ sum _ {r_ {1}} \ sum _ {r_ {2}} y_ {linear} (n_ {1} -r_ {1 } N_ {1}, n_ {2} -r_ {2} N_ {2}) {\ mathrm {\, \, \, for \, \, \,}} (n_ {1}, n_ {2}) \ v R_ ​​{N_ {1} N_ {2}}}$

Potom, aby se zabránilo aliasing mezi prostorově aliasem repliky, a musí být zvoleny tak, aby splňovaly tyto podmínky: ${\ displaystyle N_ {1}}$${\ displaystyle N_ {2}}$

${\ Displaystyle N_ {1} \ geq P_ {1}+Q_ {1} -1}$

${\ Displaystyle N_ {2} \ geq P_ {2}+Q_ {2} -1}$

Pokud jsou tyto podmínky splněny, pak se výsledky kruhové konvoluce budou rovnat výsledkům lineární konvoluce (přičemž hlavní periodu kruhové konvoluce vezmeme jako oblast podpory). To je:

${\ Displaystyle y_ {circle} (n_ {1}, n_ {2}) = y_ {linear} (n_ {1}, n_ {2})}$ pro ${\ Displaystyle (n_ {1}, n_ {2}) \ v R_ ​​{N_ {1} N_ {2}}}$

Shrnutí postupu pomocí DFT

Konvoluční větu a kruhovou konvoluci lze tedy použít následujícím způsobem k dosažení výsledku, který se rovná provedení lineární konvoluce:

1. Vybírejte a k uspokojení a${\ displaystyle N_ {1}}$${\ displaystyle N_ {2}}$${\ Displaystyle N_ {1} \ geq P_ {1}+Q_ {1} -1}$${\ Displaystyle N_ {2} \ geq P_ {2}+Q_ {2} -1}$
2. Nulové vyvěšení signálů a to tak, že oba mají velikost${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle x (n_ {1}, n_ {2})}$${\ displaystyle N_ {1} \ times N_ {2}}$
3. Vypočítejte DFT obou a${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle x (n_ {1}, n_ {2})}$
4. Chcete -li získat výsledky DFT, znásobte je ${\ Displaystyle Y (k_ {1}, k_ {2}) = H (k_ {1}, k_ {2}) X (k_ {1}, k_ {2})}$
5. Výsledek IDFT bude potom roven výsledku provedení lineární konvoluce na dva signály${\ Displaystyle Y (k_ {1}, k_ {2})}$

Překryjte a přidejte

Další metodou provádění vícerozměrné konvoluce je přístup s překrytím a přidáním . Tato metoda pomáhá snížit výpočetní náročnost často spojenou s vícerozměrnými konvolucemi kvůli velkému množství dat obsažených v moderních digitálních systémech. Kvůli stručnosti je jako příklad použit dvojrozměrný případ, ale stejné koncepty lze rozšířit na více dimenzí.

Zvažte dvourozměrnou konvoluci pomocí přímého výpočtu:

${\ Displaystyle y (n_ {1}, n_ {2}) = \ sum _ {k_ {1} =-\ infty}^{\ infty} \ sum _ {k_ {2} =-\ infty}^{\ infty} x (n_ {1} -k_ {1}, n_ {2} -k_ {2}) h (k_ ​​{1}, k_ {2})}$

Za předpokladu, že výstupní signál má N nenulových koeficientů a impulzní odezva má M nenulových vzorků, tento přímý výpočet by pro výpočet potřeboval násobky MN a sčítání MN - 1. Místo toho pomocí FFT by frekvenční odezva filtru a Fourierova transformace vstupu musely být uloženy v paměti. Velké množství výpočtů a nadměrné využívání paměťového úložného prostoru představuje problém, protože se přidávají další dimenze. Zde přichází na řadu metoda překrývání a přidávání konvoluce. ${\ displaystyle y (n_ {1}, n_ {2})}$

Rozklad na menší konvoluční bloky

Místo provádění konvoluce na blocích informací v jejich úplnosti mohou být informace rozděleny na menší bloky rozměrů x, což má za následek menší FFT, menší výpočetní složitost a menší potřebu úložiště. To lze matematicky vyjádřit následovně: ${\ displaystyle L_ {1}}$${\ displaystyle L_ {2}}$

${\ Displaystyle x (n_ {1}, n_ {2}) = \ sum _ {i = 1}^{P_ {1}} \ sum _ {j = 1}^{P_ {2}} x_ {ij} (n_ {1}, n_ {2})}$

kde představuje vstupní signál x , což je součet blokových segmentů, s a . ${\ displaystyle x (n_ {1}, n_ {2})}$${\ displaystyle N_ {1}}$${\ displaystyle N_ {2}}$${\ displaystyle P_ {1} P_ {2}}$${\ displaystyle P_ {1} = N_ {1}/L_ {1}}$${\ displaystyle P_ {2} = N_ {2}/L_ {2}}$

K produkci výstupního signálu se provádí dvourozměrná konvoluce:

${\ Displaystyle y (n_ {1}, n_ {2}) = x (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2})}$

Náhradou za výsledky získáte následující: ${\ displaystyle x (n_ {1}, n_ {2})}$

${\ Displaystyle y (n_ {1}, n_ {2}) = \ sum _ {i = 1}^{P_ {1}} \ sum _ {j = 1}^{P_ {2}} x_ {ij} (n_ {1}, n_ {2}) ** h (n_ {1}, n_ {2})}$

Tato konvoluce přináší větší složitost než provádění přímé konvoluce; vzhledem k tomu, že je integrován s rychlou konvolucí FFT, funkce overlap-add funguje rychleji a je paměťově efektivnější metodou, což je praktické pro velké sady vícerozměrných dat.

Rozpis postupu

Nechť má velikost : ${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle M_ {1} \ times M_ {2}}$

1. Rozdělte vstup na nepřekrývající se bloky dimenzí .${\ displaystyle x (n_ {1}, n_ {2})}$${\ displaystyle L_ {1} \ times L_ {2}}$
2. Nulová podložka tak, aby měla rozměry ( ) ( ).${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle L_ {1}+M_ {1} -1}$${\ displaystyle \ times}$${\ displaystyle L_ {2}+M_ {2} -1}$
3. K získání použijte DFT .${\ Displaystyle H (k_ {1}, k_ {2})}$
4. Pro každý vstupní blok:
   1. Nulová podložka má rozměry ( ) ( ).${\ displaystyle x_ {ij} (n_ {1}, n_ {2})}$${\ displaystyle L_ {1}+M_ {1} -1}$${\ displaystyle \ times}$${\ displaystyle L_ {2}+M_ {2} -1}$
   2. Vezměte diskrétní Fourierovu transformaci každého bloku .${\ displaystyle X_ {ij} (k_ {1}, k_ {2})}$
   3. Znásobením získáte .${\ Displaystyle Y_ {ij} (k_ {1}, k_ {2}) = X_ {ij} (k_ {1}, k_ {2}) H (k_ {1}, k_ {2})}$
   4. Vezměte inverzní diskrétní Fourierovu transformaci, abyste získali .${\ displaystyle Y_ {ij} (k_ {1}, k_ {2})}$${\ displaystyle y_ {ij} (n_ {1}, n_ {2})}$
5. Najděte výsledek překrytím a přidáním posledních vzorků k prvním vzorkům, abyste získali výsledek.${\ displaystyle y (n_ {1}, n_ {2})}$${\ displaystyle (M_ {1} -1)}$${\ displaystyle \ times}$ ${\ displaystyle (M_ {2} -1)}$${\ displaystyle y_ {ij} (n_ {1}, n_ {2})}$${\ displaystyle (M_ {1} -1)}$ ${\ displaystyle \ times}$${\ displaystyle (M_ {2} -1)}$${\ Displaystyle y_ {i+1, j+1} (n_ {1}, n_ {2})}$

Obrazový způsob provozu

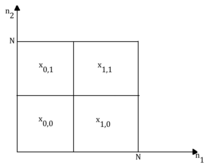
Aby byla metoda překrytí-přidání vizualizována jasněji, následující ilustrace zkoumají metodu graficky. Předpokládejme, že vstup má podporu čtvercové oblasti o délce N ve svislém i vodorovném směru, jak ukazuje obrázek níže. Poté je rozdělen na čtyři menší segmenty takovým způsobem, že je nyní složen ze čtyř menších čtverců. Každý blok souhrnného signálu má rozměry .${\ displaystyle x (n_ {1}, n_ {2})}$${\ displaystyle (N/2)}$ ${\ displaystyle \ times}$ ${\ displaystyle (N/2)}$

Poté je každá součást spojena s impulzní odezvou filtru. Všimněte si, že výhodu pro implementaci, jako je tato, lze vizualizovat zde, protože každou z těchto konvolucí lze paralelizovat na počítači, pokud má počítač dostatečnou paměť a prostředky pro ukládání a výpočet současně.

Na obrázku níže první graf vlevo představuje konvoluci odpovídající složce vstupu s odpovídající impulzní odezvou . Vpravo od toho je pak vstup spojen s impulzní odezvou . ${\ displaystyle x_ {0,0}}$${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle x_ {1,0}}$${\ displaystyle h (n_ {1}, n_ {2})}$

Stejný proces se provádí pro další dva vstupy, respektive, a jsou shromážděny dohromady, aby vytvořily konvoluci. Toto je znázorněno vlevo.

Předpokládejme, že impulsní odezva filtru má v obou dimenzích oblast podpory . To znamená, že každá konvoluce spojuje signály s rozměry v obou směrech a směrech, což vede k překrývání (zvýrazněno modře), protože délka každé jednotlivé konvoluce je ekvivalentní: ${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle (N/8)}$${\ displaystyle (N/2)}$ ${\ displaystyle \ times}$ ${\ displaystyle (N/8)}$${\ displaystyle n_ {1}}$${\ displaystyle n_ {2}}$

${\ displaystyle (N/2)}$ ${\ displaystyle +}$${\ displaystyle (N/8)}$ ${\ displaystyle -}$${\ displaystyle 1}$ = ${\ Displaystyle (5/8) N-1}$

v obou směrech. Světlejší modrá část koreluje s překrytím mezi dvěma sousedními závity, zatímco tmavší modrá část koreluje s překrytím mezi všemi čtyřmi závity. Všechny tyto překrývající se části se kromě konvolucí sčítají, aby se vytvořila kombinovaná konvoluce . ${\ displaystyle y (n_ {1}, n_ {2})}$

Překryjte a uložte

Metoda překrývání a ukládání, stejně jako metoda překrývání a přidávání, se také používá ke snížení výpočetní složitosti spojené se závity v diskrétním čase. Tato metoda ve spojení s FFT umožňuje filtrovat obrovské množství dat digitálním systémem a zároveň minimalizovat potřebný paměťový prostor používaný pro výpočty na masivních polích dat.

Porovnání s překrytím a přidáním

Metoda překrývání a ukládání je velmi podobná metodám překrývání a přidávání s několika významnými výjimkami. Metoda přidávání překrývání zahrnuje lineární konvoluci signálů diskrétního času, zatímco metoda ukládání s překrytím zahrnuje princip kruhové konvoluce. Metoda překrývání a ukládání navíc používá pouze jednorázové nulové polstrování impulsní odezvy, zatímco metoda přidávání překrytí zahrnuje nulové odsazení pro každou konvoluci na každé vstupní komponentě. Místo použití nulové výplně k zabránění aliasingu v časové oblasti, jako je její protějšek s přidáním překrytí, funkce overlap-save jednoduše zahodí všechny body aliasingu a uloží předchozí data do jednoho bloku, který bude zkopírován do konvoluce pro další blok.

V jedné dimenzi jsou rozdíly v metrikách výkonu a úložiště mezi těmito dvěma metodami minimální. V případě vícerozměrné konvoluce je však z hlediska rychlosti a úložných schopností upřednostňována metoda ukládání přesahů před metodou přidávání překrytí. Stejně jako v případě překrytí a přidání, procedura vyvolá dvojrozměrný případ, ale lze ji snadno rozšířit na všechny vícerozměrné procedury.

Rozpis postupu

Nechť má velikost : ${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle M_ {1} \ times M_ {2}}$

1. Vložte sloupce a řádky nul na začátek vstupního signálu v obou rozměrech.${\ displaystyle (M_ {1} -1)}$${\ displaystyle (M_ {2} -1)}$${\ displaystyle x (n_ {1}, n_ {2})}$
2. Rozdělte odpovídající signál na překrývající se segmenty dimenzí ( ) ( ), ve kterých se bude překrývat každý dvourozměrný blok .${\ displaystyle L_ {1}+M_ {1} -1}$${\ displaystyle \ times}$${\ displaystyle L_ {2}+M_ {2} -1}$${\ displaystyle (M_ {1} -1)}$ ${\ displaystyle \ times}$ ${\ displaystyle (M_ {2} -1)}$
3. Nulová podložka tak, aby měla rozměry ( ) ( ).${\ displaystyle h (n_ {1}, n_ {2})}$${\ displaystyle L_ {1}+M_ {1} -1}$${\ displaystyle \ times}$${\ displaystyle L_ {2}+M_ {2} -1}$
4. K získání použijte DFT .${\ Displaystyle H (k_ {1}, k_ {2})}$
5. Pro každý vstupní blok:
   1. Vezměte diskrétní Fourierovu transformaci každého bloku .${\ displaystyle X_ {ij} (k_ {1}, k_ {2})}$
   2. Znásobením získáte .${\ Displaystyle Y_ {ij} (k_ {1}, k_ {2}) = X_ {ij} (k_ {1}, k_ {2}) H (k_ {1}, k_ {2})}$
   3. Vezměte inverzní diskrétní Fourierovu transformaci, abyste získali .${\ displaystyle Y_ {ij} (k_ {1}, k_ {2})}$${\ displaystyle y_ {ij} (n_ {1}, n_ {2})}$
   4. Zbavte se prvního pro každý výstupní blok .${\ displaystyle (M_ {1} -1)}$${\ displaystyle \ times}$${\ displaystyle (M_ {2} -1)}$${\ displaystyle y_ {ij} (n_ {1}, n_ {2})}$
6. Vyhledejte připojením posledních vzorků pro každý výstupní blok .${\ displaystyle y (n_ {1}, n_ {2})}$${\ displaystyle (L_ {1} \ times L_ {2})}$${\ displaystyle y_ {ij} (n_ {1}, n_ {2})}$

Transformace šroubovice

Podobně jako při rozkladu ve sloupcovém řádku transformace šroubovice vypočítává vícerozměrnou konvoluci začleněním jednorozměrných konvolučních vlastností a operátorů. Namísto použití oddělitelnosti signálů však mapuje karteziánský souřadnicový prostor na šroubovicový souřadnicový prostor, což umožňuje mapování z vícerozměrného prostoru do jednorozměrného prostoru.

Multidimenzionální konvoluce s jednorozměrnými metodami konvoluce

Abychom porozuměli transformaci šroubovice, je užitečné nejprve porozumět tomu, jak lze vícedimenzionální konvoluci rozdělit na jednorozměrnou konvoluci. Předpokládejme, že dva signály, které mají být spojeny, jsou a , což má za následek výstup . To je vyjádřeno následovně: ${\ displaystyle X_ {M \ times N}}$${\ displaystyle Y_ {K \ times L}}$${\ displaystyle Z _ {(M-K+1) \ times (N-L+1)}}$

${\ Displaystyle Z (i, j) = \ sum _ {m = 0}^{M-1} \ sum _ {n = 0}^{N-1} X (m, n) Y (im, jn) }$

Dále se vytvoří dvě matice, které vynulují každý vstup v obou dimenzích tak, že každý vstup má ekvivalentní rozměry, tzn

${\ displaystyle \ mathbf {X '} = {\ begin {bmatrix} X & 0 \\ 0 & 0 \\\ end {bmatrix}}}$ a ${\ displaystyle \ mathbf {Y '} = {\ begin {bmatrix} Y & 0 \\ 0 & 0 \\\ end {bmatrix}}}$

kde každá ze vstupních matic má nyní rozměry . Potom je možné implementovat lexikografické řazení po sloupcích za účelem převodu upravených matic na vektory a . Aby se minimalizoval počet nevýznamných vzorků v každém vektoru, každý vektor je zkrácen po poslední vzorek v originálním matricích a resp. Vzhledem k tomu je délka vektoru a jsou dány: ${\ displaystyle (M+K-1)}$${\ displaystyle \ times}$${\ displaystyle (N+L-1)}$${\ displaystyle X ''}$${\ displaystyle Y ''}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle X ''}$${\ displaystyle Y ''}$

${\ displaystyle l_ {X ''} =}$ ${\ displaystyle (M+K-1)}$${\ displaystyle \ times}$${\ displaystyle (N-1)}$ + ${\ displaystyle M}$

${\ displaystyle l_ {Y ''} =}$${\ displaystyle (M+K-1)}$${\ displaystyle \ times}$${\ displaystyle (L-1)}$ + ${\ displaystyle K}$

Délka konvoluce těchto dvou vektorů může být odvozena a ukázána jako: ${\ displaystyle Z ''}$

${\ displaystyle l_ {Z ''} =}$ ${\ displaystyle l_ {Y ''}+}$${\ displaystyle l_ {X ''}}$ ${\ displaystyle = (M+K-1)}$${\ displaystyle \ times}$${\ displaystyle (N+L-1)}$

Tato vektorová délka je ekvivalentní rozměrům výstupu původní matice , což činí z převodu zpět na matici přímou transformaci. Vektor je tedy převeden zpět do maticové formy, která produkuje výstup dvojrozměrné diskrétní konvoluce. ${\ displaystyle Z}$${\ displaystyle Z ''}$

Filtrování na šroubovici

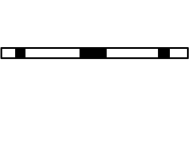
Při práci na dvourozměrné karteziánské síti bude mít Fourierova transformace podél obou os za následek, že se z dvojrozměrné roviny stane válec, protože konec každého sloupce nebo řady se připojí k příslušnému vrcholu a vytvoří válec. Filtrování na šroubovici se chová podobným způsobem, kromě tohoto případu se spodní část každého sloupce připojí k horní části dalšího sloupce, což má za následek šroubovicovou síť. To je znázorněno níže. Tmavé dlaždice představují koeficienty filtru.

Pokud je tato šroubovicová struktura rozřezána a odvinuta do jednorozměrného pásu, stejné koeficienty filtru na 2-d karteziánské rovině budou odpovídat stejným vstupním datům, což má za následek ekvivalentní schéma filtrování. Tím je zajištěno, že dvourozměrnou konvoluci bude možné provádět pomocí jednorozměrného operátoru konvoluce, protože 2D filtr byl navinut na 1D filtr s mezerami nul oddělujícími koeficienty filtru.

Za předpokladu, že byl použit nějaký nízkoprůchodový dvourozměrný filtr, například:

0	-1	0
-1	4	-1
0	-1	0

Poté, co byl dvourozměrný prostor převeden na šroubovici, bude jednorozměrný filtr vypadat následovně:

${\ Displaystyle h (n) =-1,0, ..., 0, -1,4, -1,0, ..., 0, -1,0, ...}$

Všimněte si v jednorozměrném filtru, že po odvinutí neexistují žádné počáteční nuly, jak je znázorněno na jednorozměrném filtračním pásu. Mohl být spleten celý jednorozměrný pás; je však méně výpočetně nákladné jednoduše ignorovat úvodní nuly. Navíc žádná z těchto nulových hodnot na zadní straně nebude muset být uložena v paměti, aby se zachovaly cenné prostředky paměti.

Aplikace

Helix transformace k implementaci rekurzivních filtrů pomocí konvoluce se používají v různých oblastech zpracování signálu. Ačkoli Fourierova analýza frekvenční domény je účinná, když jsou systémy nehybné, s konstantními koeficienty a periodicky vzorkovanými daty, v nestabilních systémech je to obtížnější. Helix transformace umožňuje trojrozměrné post-stackové migrační procesy, které mohou zpracovávat data pro trojrozměrné variace rychlosti. Kromě toho může být aplikován na pomoc s problémem implicitní extrapolace trojrozměrného vlnového pole. Mezi další aplikace patří užitečné algoritmy v regularizaci seismických dat, filtry predikčních chyb a útlum hluku v geofyzikálních digitálních systémech.

Gaussova konvoluce

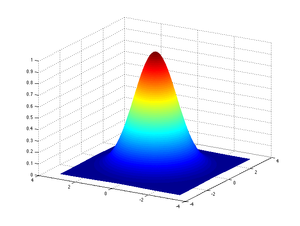
Jednou aplikací vícerozměrné konvoluce, která se používá při zpracování signálu a obrazu, je Gaussova konvoluce. To se týká konvoluce vstupního signálu s Gaussovou distribuční funkcí.

Gaussova distribuce vzorkovaná na diskrétních hodnotách v jedné dimenzi je dána následujícím (za předpokladu ):${\ Displaystyle \ mu = 0}$

To je snadno rozšířeno na signál M dimenzí (za předpokladu, že zůstává konstantní pro všechny dimenze a ):${\ Displaystyle \ sigma}$${\ Displaystyle \ mu _ {1} = \ mu _ {2} = ... = \ mu _ {M} = 0}$Jednou důležitou vlastností, kterou je třeba rozpoznat, je to, že M rozměrný signál je oddělitelný tak, že:Pak lze Gaussovu konvoluci s signály s diskrétní hodnotou vyjádřit následovně:

${\ Displaystyle y (n) = x (n)*G (n)}$

${\ Displaystyle y (n_ {1}, n_ {2}, ..., n_ {M}) = x (n_ {1}, n_ {2}, ..., n_ {M})*... *G (n_ {1}, n_ {2}, ..., n_ {M})}$

Přibližování pomocí FIR filtru

Gaussovu konvoluci lze účinně aproximovat implementací filtru FIR ( Finite Impuls Response ). Filtr bude navržen se zkrácenými verzemi Gaussova. U dvourozměrného filtru by byla přenosová funkce takového filtru definována následovně:

${\ Displaystyle H (z_ {1}, z_ {2}) = {\ frac {1} {s (r_ {1}, r_ {2})}} \ sum _ {n_ {1} =-r_ {1 }}^{r_ {1}} \ sum _ {n_ {2} =-r_ {2}}^{r_ {2}} G (n_ {1}, n_ {2}) {z_ {1}}^ {-n_ {1}} {z_ {2}}^{-n_ {2}}}$

kde

${\ Displaystyle s (r_ {1}, r_ {2}) = \ sum _ {n_ {1} =-r_ {1}}^{r_ {1}} \ sum _ {n_ {2} =-r_ { 2}}^{r_ {2}} G (n_ {1}, n_ {2})}$

Volba nižších hodnot pro a bude mít za následek menší počet výpočtů, ale přinese méně přesné přiblížení, zatímco výběr vyšších hodnot poskytne přesnější aproximaci, ale bude vyžadovat větší počet výpočtů. ${\ displaystyle r_ {1}}$${\ displaystyle r_ {2}}$

Přibližování pomocí boxového filtru

Další metodou aproximace Gaussovy konvoluce je rekurzivní průchod přes boxový filtr. Pro aproximaci jednorozměrné konvoluce je tento filtr definován jako následující:

${\ Displaystyle H (z) = {\ frac {1} {2r+1}} {\ frac {z^{r} -z^{-r-1}} {1-z^{-} 1}} }$

Aby se získala přesná aproximace, obvykle se provádějí rekurzivní průchody 3, 4 nebo 5krát. Navrhovaná metoda pro výpočet r je pak uvedena jako následující:

${\ Displaystyle \ sigma ^{2} = {\ frac {1} {12}} K ((2r+1) ^{2} -1)}$ kde K je počet rekurzivních průchodů filtrem.

Potom, protože Gaussova distribuce je oddělitelná napříč různými dimenzemi, z toho vyplývá, že rekurzivní prochází jednorozměrnými filtry (izolace každé dimenze samostatně) tedy poskytne aproximaci vícerozměrné gaussovské konvoluce. To znamená, že M- dimenzionální Gaussovu konvoluci lze aproximovat pomocí rekurzivních průchodů následujícími jednorozměrnými filtry:

${\ Displaystyle H (z_ {1}) = {\ frac {1} {2r_ {1} +1}} {\ frac {{z_ {1}}^{r_ {1}}-{z_ {1}} ^{-r_ {1} -1}} {1- {z_ {1}}^{-} 1}}}$

${\ Displaystyle H (z_ {2}) = {\ frac {1} {2r_ {2} +1}} {\ frac {{z_ {2}}^{r_ {2}}-{z_ {2}} ^{-r_ {2} -1}} {1- {z_ {2}}^{-} 1}}}$

${\ Displaystyle \ vdots}$

${\ Displaystyle H (z_ {M}) = {\ frac {1} {2r_ {M} +1}} {\ frac {{z_ {M}}^{r_ {M}}-{z_ {M}} ^{-r_ {M} -1}} {1- {z_ {M}}^{-} 1}}}$

Aplikace

Gaussovy závity se široce používají při zpracování signálu a obrazu. Například rozmazání obrazu lze provést pomocí Gaussovy konvoluce, kde parametr bude řídit sílu rozmazání. Vyšší hodnoty by tedy odpovídaly rozmazanějšímu konečnému výsledku. To je také běžně používané v aplikacích počítačového vidění , jako je detekce funkcí SIFT ( Scale-invariant feature transform ). ${\ Displaystyle \ sigma}$

Viz také

• Konvoluce
• Jádro (zpracování obrazu)
• Zpracování signálu

Reference