Nielsenova – Schreierova věta - Nielsen–Schreier theorem

V teorii skupiny , odvětví matematiky se Nielsen-Schreier věta říká, že každá podskupina z volné skupiny je sám zdarma. Je pojmenována po Jakobovi Nielsenovi a Otto Schreierovi .

Prohlášení o větě

Volnou skupinu lze definovat ze skupinové prezentace sestávající ze sady generátorů bez vztahů. To znamená, že každý prvek je produktem nějaké sekvence generátorů a jejich inverzí, ale tyto prvky se neřídí žádnými rovnicemi kromě těch, které triviálně vyplývají z gg −1 = 1. Prvky volné skupiny lze popsat jako všechna možná redukovaná slova , ty řetězce generátorů a jejich inverzí, ve kterých žádný generátor sousedí s vlastní inverzí. Dvě redukovaná slova lze vynásobit jejich zřetězením a poté odstraněním jakýchkoli generátorově inverzních párů, které jsou výsledkem zřetězení.

Nielsen-Schreier věta se uvádí, že v případě, H je podskupina volné skupiny G , pak H je sám izomorfní na volnou skupinu. To znamená, že existuje stanovený S prvků, které vytvářejí H , s žádnými netriviální vztahy mezi prvky S .

Nielsen-Schreier vzorec nebo Schreier index vzorec , kvantifikuje výsledek v případě, kdy je podskupina konečný index: pokud G je volná skupina hodnosti n (bez na n generátory), a H je podskupina konečného indexu [ G  : H ] = e , pak H je bez hodnosti .

Příklad

Nechť G je volná skupina se dvěma generátory a H je podskupina skládající se ze všech redukovaných slov sudé délky (součin sudého počtu písmen ). Potom je H generováno jeho šesti prvky A faktorizaci jakéhokoli redukovaného slova v H do těchto generátorů a jejich inverzí lze sestrojit jednoduše tak, že vezmeme po sobě jdoucí dvojice písmen v redukovaném slově. Nejde však o bezplatnou prezentaci H, protože poslední tři generátory lze zapsat jako první tři jako . H je spíše generováno jako volná skupina třemi prvky, které mezi sebou nemají žádné vztahy; nebo místo toho několika dalšími trojicemi šesti generátorů. Dále G je volné na n = 2 generátorech, H má index e = [ G  : H ] = 2 v G a H je volné na 1 + e ( n –1) = 3 generátorech. Věta Nielsen – Schreier uvádí, že stejně jako H lze každou podskupinu volné skupiny generovat jako volnou skupinu, a pokud je index H konečný, je jeho hodnost dána indexovým vzorcem.

Důkaz

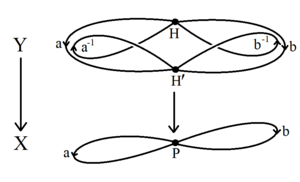
Volná skupina G = π 1 ( X ) má n = 2 generátory odpovídajících smyček s , b od referenční bod P na X . Podskupina H o i délky slovy, index e = [ G  : H ] = 2, odpovídá krytí graf Y se dvěma vrcholy, které odpovídají cosets H a H‘ = aH = bH = -1 H = b - 1 H a dva zvednuté okraje pro každý z původních okrajů smyčky a , b . Smršťování jednoho z okrajů Y dává homotopickou ekvivalenci kytici tří kruhů, takže H = π 1 ( Y ) je volná skupina na třech generátorech, například aa , ab , ba .

Krátký důkaz Nielsen-Schreier teorému používá algebraické topologie z základních skupin, a pokrývající prostor . Volná skupina G na sadě generátorů je základní skupinou kytice kruhů , topologického grafu X s jediným vrcholem a okrajem smyčky pro každý generátor. Jakákoli podskupina H základní skupiny je sama o sobě základní skupinou propojeného krycího prostoru Y → X. Prostor Y je (možná nekonečný) topologický graf, Schreierův graf grafu má jeden vrchol pro každý coset v G/H . V každém připojené topologické grafu, je možné zmenšit okrajů kostry grafu, produkovat kytici kruhů, který má stejné základní skupiny H . Protože H je základní skupina kytice kruhů, je sama o sobě volná.

Simpliciální homologie umožňuje výpočet hodnosti H , která se rovná h 1 ( Y ), první Bettiho číslo krycího prostoru, počet nezávislých cyklů. Pro G bez hodnosti n , graf X má n hran a 1 vrchol; za předpokladu, že atom vodíku je konečný index [ G  : H ] = e , krycí graf Y má en hranami a e vrcholy. První Bettiho číslo grafu se rovná počtu hran minus počet vrcholů plus počet spojených komponent; hodnost H je tedy:

Tento důkaz mají Reinhold Baer a Friedrich Levi  ( 1936 ); původní doklad o Schreier tvoří graf Schreier jiným způsobem, jako kvocient Cayley grafu z G modulo působení H .

Podle Schreierova podskupinového lemmatu může být sada generátorů pro volnou prezentaci H sestrojena z cyklů v krycím grafu vytvořeném zřetězením cesty klenutého stromu ze základního bodu (soupravy identity) do jednoho z kosetů, a jeden okraj bez stromu a inverzní cesta přes strom z druhého koncového bodu okraje zpět do základního bodu.

Axiomatické základy

Ačkoli je známo několik různých důkazů Nielsen -Schreierovy věty, všechny závisí na zvoleném axiomu . V důkazu založeném například na základních skupinách kytic se axiom volby objevuje v masce tvrzení, že každý připojený graf má strom spanning. Použití tohoto axiomu je nezbytné, protože existují modely teorie množin Zermelo – Fraenkel, ve kterých jsou axiom volby a Nielsenova -Schreierova věta nepravdivé. Nielsenova -Schreierova věta zase implikuje slabší verzi zvoleného axiomu pro konečné množiny.

Dějiny

Nielsen-Schreierova věta je neabelským analogem staršího výsledku Richarda Dedekinda , že každá podskupina svobodné abelianské skupiny je svobodná abelianská .

Jakob Nielsen ( 1921 ) původně prokázal omezenou formu věty s tím, že jakákoli konečně generovaná podskupina volné skupiny je zdarma. Jeho důkaz zahrnuje provedení sekvence Nielsenových transformací na generující sadě podskupiny, které snižují jejich délku (jako redukovaná slova ve volné skupině, ze které jsou čerpány). Otto Schreier dokázal větu Nielsen-Schreier v jeho plné obecnosti v jeho 1926 habilitační práce , Die Untergruppen der freien Gruppe , také publikoval v roce 1927 v Abh. matematika. Sem. Hamburg. Univ.

Za topologický důkaz založený na základních skupinách kytic kruhů stojí Reinhold Baer a Friedrich Levi  ( 1936 ). Další topologické důkaz, založený na teorii Bass-Serre ze skupinových akcí na stromech , byl publikován Jean-Pierre Serre  ( 1970 ).

Viz také

Poznámky

Reference