Teorie čísel -Number theory

Distribuce prvočísel je ústředním bodem studia v teorii čísel. Tato ulamská spirála to slouží k ilustraci a naznačuje zejména podmíněnou nezávislost mezi prvočíslem a hodnotou určitých kvadratických polynomů.

Matematika
Čistý základy Analýza Algebra Teorie čísel Kombinatorika Geometrie Topologie Aplikovaný Pravděpodobnost Statistika Výpočetní vědy Matematická fyzika Operační výzkum Matematická optimalizace Výpočetní biologie Počítačová lingvistika
články
0–9 A B C D E F G H já J K L M N Ó P Q R S T U PROTI W X Y Z
vědci
A B C D E F G H já J K L M N Ó P Q R S T U PROTI W X Y Z
Navigace
Seznamy Obrys Portál Oblasti
proti t E

Teorie čísel (nebo aritmetika nebo vyšší aritmetika ve starším použití) je odvětví čisté matematiky věnované především studiu celých čísel a celočíselných funkcí . Německý matematik Carl Friedrich Gauss (1777–1855) řekl: „Matematika je královnou věd – a teorie čísel je královnou matematiky.“ Teoretici čísel studují prvočísla stejně jako vlastnosti matematických objektů vyrobených z celých čísel (například racionální čísla ) nebo definovaných jako zobecnění celých čísel (například algebraická celá čísla ).

Celá čísla mohou být považována buď sama o sobě, nebo jako řešení rovnic ( Diophantine geometry ). Otázky v teorii čísel jsou často nejlépe dohodnuté přes studii o analytických objektech (například, Riemann zeta funkce ) to kódovat vlastnosti celých čísel, připraví nebo jiné číslo-teoretické objekty v nějaké módě ( analytická teorie čísel ). Jeden může také studovat reálná čísla ve vztahu k racionálním číslům, například, jak aproximovaný latter ( diofantická aproximace ).

Starší termín pro teorii čísel je aritmetika . Na počátku dvacátého století byla nahrazena „teorií čísel“. (Slovo „ aritmetika “ je používáno širokou veřejností ve významu „ elementární výpočty “; získalo také další významy v matematické logice , jako je Peano aritmetika , a počítačové vědě , jako je aritmetika s plovoucí desetinnou čárkou .) aritmetika termínu pro teorii čísel znovu získala nějakou půdu ve druhé polovině 20. století, pravděpodobně z části kvůli francouzskému vlivu. Zejména aritmetický je běžně preferován jako přídavné jméno k teoriím čísel .

Dějiny

Origins

Úsvit aritmetiky

Tablet Plimpton 322

Nejstarším historickým nálezem aritmetické povahy je fragment tabulky: rozbitá hliněná tabulka Plimpton 322 ( Larsa, Mezopotámie , asi 1800 př. n. l.) obsahuje seznam „ pythagorejských trojic “, tedy celých čísel , že . Trojitých je příliš mnoho a jsou příliš velké na to, aby byly získány hrubou silou . Nadpis nad prvním sloupcem zní: " Takiltum úhlopříčky, které bylo odečteno tak, že šířka..." ${\displaystyle (a,b,c)}$${\displaystyle a^{2}+b^{2}=c^{2}}$

Rozvržení stolu naznačuje, že byl zkonstruován pomocí toho, co v moderním jazyce znamená identitu

${\displaystyle \left({\frac {1}{2}}\left(x-{\frac {1}{x}}\right)\right)^{2}+1=\left({\frac {1}{2}}\left(x+{\frac {1}{x}}\right)\right)^{2},}$

což je implicitní v rutinních starobabylonských cvičeních. Pokud byla použita nějaká jiná metoda, byly trojice nejprve zkonstruovány a poté přeřazeny podle , pravděpodobně pro skutečné použití jako "tabulka", například s ohledem na aplikace. ${\displaystyle c/a}$

Není známo, co tyto aplikace mohly být nebo zda nějaké mohly být; Babylonská astronomie se například skutečně prosadila až později. Místo toho bylo navrženo, že tabulka byla zdrojem numerických příkladů pro školní problémy.

Zatímco babylónská teorie čísel – nebo to, co přežívá z babylonské matematiky , kterou lze takto nazvat – sestává z tohoto jediného nápadného fragmentu, babylonská algebra (ve středoškolském smyslu „ algebra “) byla výjimečně dobře vyvinuta. Pozdně novoplatónské zdroje uvádějí, že se Pythagoras naučil matematiku od Babyloňanů. Mnohem dřívější zdroje uvádějí, že Thales a Pythagoras cestovali a studovali v Egyptě .

Euclid IX 21–34 je velmi pravděpodobně pythagorejský; je to velmi jednoduchý materiál ("liché časy sudé jsou sudé", "pokud liché číslo měří [= dělí] sudé číslo, měří také [= dělí] jeho polovinu"), ale je vše, co je potřeba dokázat, že je to iracionální . Pythagorejští mystici kladli velký důraz na liché a sudé. Objev, který je iracionální, je připisován raným Pythagorejcům (před Theodorem ). Odhalením (moderně řečeno), že čísla mohou být iracionální, se zdá, že tento objev vyvolal první fundamentální krizi v matematické historii; jeho důkaz nebo jeho odhalení být někdy připočítán k Hippasovi , kdo byl vyloučen nebo rozdělený od Pythagorean sekty. To si vynutilo rozlišení mezi čísly (celými čísly a racionálními – předměty aritmetiky) na jedné straně a délkami a proporcemi (které bychom ztotožnili s reálnými čísly, ať už racionálními nebo ne), na straně druhé. ${\displaystyle {\sqrt {2}}}$${\displaystyle {\sqrt {2}}}$

Pythagorejská tradice hovořila také o tzv. polygonálních nebo figurálních číslech . Zatímco čtvercová čísla , kubická čísla atd. jsou nyní považována za přirozenější než trojúhelníková čísla , pětiúhelníková čísla atd., studium součtů trojúhelníkových a pětiúhelníkových čísel se ukázalo jako plodné v raném novověku (17. až počátek 19. ).

Ve starověkých egyptských nebo védských zdrojích neznáme žádný jasně aritmetický materiál , i když v každém je nějaká algebra. Čínská věta o zbytku se objevuje jako cvičení v Sunzi Suanjing (3., 4. nebo 5. století n. l.). (V Sunziho řešení je opomenut jeden důležitý krok: je to problém, který později vyřešil Áryabhaṭův Kuṭṭaka – viz níže . )

V čínské matematice existuje také určitá numerická mystika, ale na rozdíl od pythagorejců se zdá, že nikam nevedla. Stejně jako dokonalá čísla Pythagorejců i magické čtverce přešly z pověry do rekreace .

Klasické Řecko a rané helénistické období

Kromě několika fragmentů je nám matematika klasického Řecka známá buď prostřednictvím zpráv současných nematematiků, nebo prostřednictvím matematických prací z raného helénistického období. V případě teorie čísel, toto znamená, a velký, Plato a Euclid , příslušně.

Zatímco asijská matematika ovlivnila řecké a helénistické učení, zdá se, že řecká matematika je také původní tradicí.

Eusebius , PE X, kapitola 4 zmínky o Pythagorovi :

„Zmíněný Pythagoras, zatímco pilně studoval moudrost každého národa, navštívil Babylón, Egypt a celou Persii, byl poučen mágy a kněžími: a kromě toho je příbuzný, že studoval u Brahmanů ( to jsou indičtí filozofové); a od některých shromáždil astrologii, od jiných geometrii a aritmetiku a hudbu od jiných a různé věci od různých národů a pouze od mudrců z Řecka nedostal nic, jako oni byli oddáni chudoba a nedostatek moudrosti: tak se naopak sám stal autorem poučení Řeků o učenosti, kterou získal z ciziny."

Aristoteles tvrdil, že filozofie Platóna úzce následovala učení Pythagorejců, a Cicero toto tvrzení opakuje: Platonem ferunt didicisse Pythagorea omnia („Říkají, že se Platón naučil všechny věci Pythagorejsky“).

Platón se velmi zajímal o matematiku a jasně rozlišoval mezi aritmetikou a výpočtem. ( Aritmetikou měl zčásti na mysli teoretizování o číslech, spíše než to, co aritmetika nebo teorie čísel znamenají.) Prostřednictvím jednoho z Platónových dialogů – jmenovitě Theaeteta – víme, že Theodorus dokázal, že jsou iracionální. Theaetetus byl stejně jako Platón Theodorovým žákem; on pracoval na rozlišování různých druhů incommensurables , a byl tak pravděpodobně průkopník ve studiu číselných soustav . (Knihu X Euklidových prvků popisuje Pappus jako knihu z velké části založenou na Theaetetově díle.) ${\displaystyle {\sqrt {3}},{\sqrt {5}},\dots ,{\sqrt {17}}}$

Euklides věnoval část svých Prvků prvočíslům a dělitelnosti, tématům, která do teorie čísel jednoznačně patří a jsou pro ni základní (knihy VII až IX Euklidových Prvků ). Zejména dal algoritmus pro počítání největšího společného dělitele dvou čísel ( euklidovský algoritmus ; Elements , Prop. VII.2) a první známý důkaz nekonečnosti prvočísel ( Elements , Prop. IX.20).

V 1773, Lessing publikoval epigram , který on našel v rukopise během jeho práce jako knihovník; to prohlašovalo, že je dopis poslaný Archimedes k Eratosthenes . Epigram navrhoval to, co se stalo známým jako Archimédův problém dobytka ; jeho řešení (v rukopise chybí) vyžaduje vyřešení neurčité kvadratické rovnice (která se redukuje na to, co by bylo později nesprávně pojmenováno Pellova rovnice ). Pokud víme, takové rovnice poprvé úspěšně zpracovala indická škola . Není známo, zda sám Archimedes měl způsob řešení.

Diophantus

Titulní strana vydání Diophantovy Arithmetiky z roku 1621 , kterou do latiny přeložil Claude Gaspard Bachet de Méziriac .

Velmi málo je znáno o Diophantus Alexandrie ; žil pravděpodobně ve třetím století našeho letopočtu, tedy asi pět set let po Euklidovi. Šest ze třinácti knih Diophantovy Aritmetiky přežilo v původní řečtině a čtyři další přežily v arabském překladu. Aritmetika je sbírka vypracovaných problémů, jejichž úkolem je vždy najít racionální řešení systému polynomiálních rovnic, obvykle ve tvaru nebo . V dnešní době tedy mluvíme o diofantických rovnicích , když mluvíme o polynomiálních rovnicích, pro které je třeba najít racionální nebo celočíselná řešení. ${\displaystyle f(x,y)=z^{2}}$${\displaystyle f(x,y,z)=w^{2}}$

Dalo by se říci, že Diophantus studoval racionální body, tedy body, jejichž souřadnice jsou racionální – na křivkách a algebraických varietách ; nicméně, na rozdíl od Řeků klasického období, kteří dělali to, co bychom nyní nazvali základní algebrou v geometrických termínech, Diophantus dělal to, co bychom nyní nazývali základní algebraickou geometrií v čistě algebraických termínech. V moderním jazyce, co Diophantus udělal, bylo najít racionální parametrizaci odrůd; to znamená, že vzhledem k rovnici tvaru (řekněme) bylo jeho cílem najít (v podstatě) tři racionální funkce tak, aby pro všechny hodnoty a nastavení pro poskytlo řešení${\displaystyle f(x_{1},x_{2},x_{3})=0}$ ${\displaystyle g_{1},g_{2},g_{3}}$${\displaystyle r}$${\displaystyle s}$${\displaystyle x_{i}=g_{i}(r,s)}$${\displaystyle i=1,2,3}$${\displaystyle f(x_{1},x_{2},x_{3})=0.}$

Diophantus také studoval rovnice některých neracionálních křivek, pro které není možná racionální parametrizace. Podařilo se mu najít některé racionální body na těchto křivkách ( eliptické křivky , jak se to stává, v tom, co se zdá být jejich prvním známým výskytem), pomocí čehož se rovná tečné konstrukci: převedené do souřadnicové geometrie (která v Diofantově době neexistovala). ), jeho metoda by byla vizualizována jako kreslení tečny ke křivce ve známém racionálním bodě a následné nalezení druhého průsečíku tečny s křivkou; ten další bod je nový racionální bod. (Diophantus se také uchýlil k tomu, co by se dalo nazvat zvláštním případem sekantové konstrukce.)

Zatímco Diophantus byl zaujatý velmi racionálními řešeními, on předpokládal některé výsledky na celých číslech, zvláště že každé celé číslo je součet čtyř čtverců (ačkoli on nikdy říkal jak hodně výslovně).

Áryabhaṭa, Brahmagupta, Bhāskara

Zatímco řecká astronomie pravděpodobně ovlivnila indické učení, až do té míry, že zavedla trigonometrii, zdá se, že indická matematika je jinak domorodou tradicí; konkrétně neexistuje žádný důkaz, že by se Euklidovy prvky dostaly do Indie před 18. stoletím.

Āryabhaṭa (476–550 n. l.) ukázal, že páry současných kongruencí lze vyřešit metodou, kterou nazval kuṭṭaka nebo pulveriser ; toto je postup blízký (zobecnění) euklidovského algoritmu , který byl pravděpodobně nezávisle objeven v Indii. Zdá se, že Áryabhaṭa měl na mysli aplikace pro astronomické výpočty. ${\displaystyle n\equiv a_{1}{\bmod {m}}_{1}}$${\displaystyle n\equiv a_{2}{\bmod {m}}_{2}}$

Brahmagupta (628 n. l.) zahájil systematické studium neurčitých kvadratických rovnic – zejména nesprávně pojmenované Pellovy rovnice , o kterou se Archimédes mohl zajímat jako první a která se na Západě začala řešit až v době Fermata a Eulera. Pozdější sanskrtští autoři by následovali s použitím Brahmaguptovy technické terminologie. Obecný postup ( čakravala neboli „cyklická metoda“) pro řešení Pellovy rovnice nakonec našel Jayadeva (citováno v jedenáctém století; jeho práce je jinak ztracena); nejčasnější přežívající výklad se objeví v Bhāskara II je Bīja-gaṇita (dvanácté století).

Indická matematika zůstala v Evropě až do konce osmnáctého století velkou neznámou; Práce Brahmagupty a Bhāskary přeložil do angličtiny v roce 1817 Henry Colebrooke .

Aritmetika v islámském zlatém věku

Al-Haytham z pohledu Západu: na frontispisu Selenographia Alhasen [ sic ] představuje poznání prostřednictvím rozumu a Galileiho poznání prostřednictvím smyslů.

Na počátku devátého století nařídil chalífa Al-Ma'mun překlady mnoha řeckých matematických prací a alespoň jednoho sanskrtského díla ( Sindhind , což může nebo nemusí být Brahmagupta Brāhmasphuṭasiddhānta ) . Diophantusovo hlavní dílo, Aritmetika , přeložil do arabštiny Qusta ibn Luqa (820–912). Část pojednání al-Fakhri (od al-Karajīho , 953 – cca 1029) na tom do jisté míry navazuje. Podle Rasheda Roshdiho současník Al-Karajī Ibn al-Haytham věděl, co by se později nazývalo Wilsonův teorém .

Západní Evropa ve středověku

Kromě pojednání o čtvercích v aritmetickém postupu od Fibonacciho — který cestoval a studoval v severní Africe a Konstantinopoli — se v západní Evropě během středověku nedělala žádná teorie čísel, o které by se dalo mluvit. Záležitosti se v Evropě začaly měnit v pozdní renesanci , díky obnovenému studiu děl řeckého starověku. Katalyzátorem byla textová úprava a překlad Diophantovy Arithmetiky do latiny .

Raně moderní teorie čísel

Fermat

Pierre de Fermat

Pierre de Fermat (1607–1665) své spisy nikdy nepublikoval; zvláště jeho práce o teorii čísel je téměř úplně obsažena v dopisech matematikům a v soukromých poznámkách na okraji. Ve svých poznámkách a dopisech téměř nepsal žádné důkazy - v okolí neměl žádné modely.

Během svého života, Fermat učinil následující příspěvky do této oblasti:

• Jedním z prvních Fermatových zájmů byla dokonalá čísla (která se objevují v Euklidovi, Elements IX) a přátelská čísla ; tato témata ho vedla k práci na celočíselných dělitelích , které byly od začátku mezi předměty korespondence (1636 kupředu), která ho přivedla do kontaktu s tehdejší matematickou komunitou.
• V roce 1638 Fermat bez důkazu tvrdil, že všechna celá čísla lze vyjádřit jako součet čtyř nebo méně čtverců.
• Fermatova malá věta (1640): pokud a není dělitelné prvočíslem p , pak${\displaystyle a^{p-1}\equiv 1{\bmod {p}}.}$
• Jestliže a a b jsou coprime, pak není dělitelné žádným prvočíslem kongruentem k -1 modulo 4; a každý prvočíslo kongruent k 1 modulo 4 může být zapsán ve tvaru . Tyto dva výroky pocházejí rovněž z roku 1640; v roce 1659 Fermat řekl Huygensovi, že toto druhé tvrzení dokázal metodou nekonečného sestupu .${\displaystyle a^{2}+b^{2}}$${\displaystyle a^{2}+b^{2}}$
• V roce 1657 Fermat položil problém řešení jako výzvu anglickým matematikům. Problém za pár měsíců vyřešili Wallis a Brouncker. Fermat považoval jejich řešení za platné, ale poukázal na to, že poskytli algoritmus bez důkazu (stejně jako Jayadeva a Bhaskara, ačkoli Fermat si toho nebyl vědom). Uvedl, že důkaz lze nalézt nekonečným sestupem.${\displaystyle x^{2}-Ny^{2}=1}$
• Fermat uvedl a dokázal (nekonečným sestupem) v příloze k Pozorování Diofanta (Obs. XLV), že nemá žádná netriviální řešení v celých číslech. Fermat také zmínil svým korespondentům, že nemá žádná netriviální řešení a že to lze dokázat i nekonečným sestupem. První známý důkaz je způsoben Eulerem (1753; skutečně nekonečným původem).${\displaystyle x^{4}+y^{4}=z^{4}}$${\displaystyle x^{3}+y^{3}=z^{3}}$
• Fermat tvrdil ( Fermatův poslední teorém ), že ukázal, že neexistují žádná řešení pro všechny ; toto tvrzení se objevuje v jeho anotacích na okraji jeho kopie Diophanta.${\displaystyle x^{n}+y^{n}=z^{n}}$${\displaystyle n\geq 3}$

Euler

Leonhard Euler

Zájem Leonharda Eulera (1707–1783) o teorii čísel poprvé podnítil v roce 1729, kdy ho jeho přítel, amatér Goldbach , upozornil na některé Fermatovy práce na toto téma. Toto bylo nazýváno “znovuzrozením” moderní teorie čísel, po Fermatově relativním nedostatku úspěchu při získávání pozornosti jeho současníků pro toto téma. Eulerova práce na teorii čísel zahrnuje následující:

• Důkazy pro Fermatova tvrzení. To zahrnuje Fermatův malý teorém (zobecněný Eulerem na moduly bez prvočísla); skutečnost, že tehdy a jen tehdy , když ; počáteční práce na důkazu, že každé celé číslo je součtem čtyř čtverců (první úplný důkaz je od Josepha-Louise Lagrange (1770), brzy vylepšený samotným Eulerem); nedostatek nenulových celočíselných řešení (implikující případ n=4 poslední Fermatovy věty, případ n=3 , jehož Euler také dokázal příbuznou metodou).${\displaystyle p=x^{2}+y^{2}}$${\displaystyle p\equiv 1{\bmod {4}}}$${\displaystyle x^{4}+y^{4}=z^{2}}$
• Pellova rovnice , poprvé nesprávně pojmenovaná Eulerem. Psal o spojení mezi pokračujícími zlomky a Pellovou rovnicí.
• První kroky k analytické teorii čísel . Ve své práci součtů čtyř čtverců, oddílů , pětiúhelníkových čísel a distribuce prvočísel Euler propagoval použití toho, co lze považovat za analýzu (zejména nekonečné řady) v teorii čísel. Protože žil před rozvojem komplexní analýzy , většina jeho práce se omezuje na formální manipulaci s mocninnými řadami . On dělal, nicméně, dělat některé velmi pozoruhodné (ačkoli ne úplně pečlivé) rané práce na čem by později byl volán Riemann zeta funkce .
• Kvadratické formy . Po Fermatově vedení provedl Euler další výzkum otázky, která prvočísla mohou být vyjádřena ve formě , z nichž některá předznamenávají kvadratickou reciprocitu .${\displaystyle x^{2}+Ny^{2}}$
• Diofantické rovnice . Euler pracoval na některých Diophantine rovnicích rodu 0 a 1. Zejména studoval Diophantovu práci; snažil se to systematizovat, ale čas pro takový pokus ještě nedozrál – algebraická geometrie byla teprve v plenkách. Všiml si, že existuje souvislost mezi diofantickými problémy a eliptickými integrály , jejichž studium sám inicioval.

"Nastal problém, kterému jsem, 10 let, porozuměl, a od té chvíle jsem věděl, že ho nikdy nenechám být. Musel jsem ho vyřešit." – Sir Andrew Wiles o svém důkazu Fermatovy poslední věty .

Lagrange, Legendre a Gauss

Carl Friedrich Gauss 's Disquisitiones Arithmeticae , první vydání

Joseph-Louis Lagrange (1736–1813) byl první, kdo poskytl úplné důkazy některých Fermatových a Eulerových prací a pozorování – například větu o čtyřech čtvercích a základní teorii nesprávně pojmenované „Pellovy rovnice“ (pro kterou byl vytvořen algoritmus řešení nalezli Fermat a jeho současníci a také Jayadeva a Bhaskara II před nimi.) Studoval také kvadratické formy v plné obecnosti (na rozdíl od ) – definoval jejich vztah ekvivalence, ukázal, jak je dát do redukované formy atd. ${\displaystyle mX^{2}+nY^{2}}$

Adrien-Marie Legendre (1752–1833) jako první vyslovil zákon kvadratické reciprocity. Také se domníval, co se rovná teorému o prvočíslu a Dirichletově teorému o aritmetických posloupnostech . Dal úplné zpracování rovnice a pracoval na kvadratických formách podél linií, které později plně vyvinul Gauss. Ve svém stáří jako první dokázal Fermatovu poslední větu pro (dokončení práce Petera Gustava Lejeuna Dirichleta a připisování jeho i Sophie Germainové ). ${\displaystyle ax^{2}+by^{2}+cz^{2}=0}$${\displaystyle n=5}$

Carl Friedrich Gauss

Carl Friedrich Gauss (1777–1855) ve svých Disquisitiones Arithmeticae (1798) dokázal zákon kvadratické reciprocity a rozvinul teorii kvadratických forem (zejména definoval jejich složení). Zavedl také některé základní zápisy ( kongruence ) a věnoval část výpočetním záležitostem, včetně testů primality. Poslední část Disquisitiones vytvořila spojení mezi kořeny jednoty a teorií čísel:

Teorie dělení kruhu...která je pojednána v kap. 7 nepatří sám o sobě do aritmetiky, ale její principy lze čerpat pouze z vyšší aritmetiky.

Tímto způsobem Gauss pravděpodobně učinil první vpád k práci Évarista Galoise a algebraické teorii čísel .

Zralost a rozdělení do podoborů

Ernst Kummer

Peter Gustav Lejeune Dirichlet

Počínaje začátkem devatenáctého století postupně došlo k následujícímu vývoji:

• Vzestup k sebeuvědomění teorie čísel (nebo vyšší aritmetiky ) jako studijního oboru.
• Vývoj velké části moderní matematiky nezbytný pro základní moderní teorii čísel: komplexní analýza , teorie grup , Galoisova teorie — doprovázená větší přísností v analýze a abstrakci v algebře.
• Hrubé rozdělení teorie čísel na její moderní podoblasti – zejména analytickou a algebraickou teorii čísel.

Dá se říci, že algebraická teorie čísel začíná studiem reciprocity a cyklotomie , ale skutečně se prosadila s rozvojem abstraktní algebry a rané ideální teorie a teorie oceňování ; viz. níže. Konvenčním výchozím bodem pro analytickou teorii čísel je Dirichletova věta o aritmetických postupech (1837), jejíž důkaz zavedl L-funkce a zahrnoval určitou asymptotickou analýzu a omezující proces na reálné proměnné. První použití analytických myšlenek v teorii čísel ve skutečnosti sahá až k Eulerovi (30. léta 18. století), který používal formální mocninné řady a nerigorózní (nebo implicitní) omezující argumenty. Použití komplexní analýzy v teorii čísel přijde později: práce Bernharda Riemanna (1859) na funkci zeta je kanonický výchozí bod; Jacobiho čtyř-čtvercový teorém (1839), který jej předchází, patří k původně odlišnému prvku, který nyní převzal vedoucí roli v analytické teorii čísel ( modulární formy ).

Historie každého podpole je stručně popsána v samostatné části níže; viz hlavní článek každého podpole pro podrobnější ošetření. Mnoho nejzajímavějších otázek v každé oblasti zůstává otevřených a aktivně se na nich pracuje.

Hlavní pododdělení

Elementární teorie čísel

Termín elementární obecně označuje metodu, která nepoužívá komplexní analýzu . Například teorém o prvočíslech byl poprvé prokázán pomocí komplexní analýzy v roce 1896, ale elementární důkaz byl nalezen až v roce 1949 Erdősem a Selbergem . Termín je poněkud nejednoznačný: například důkazy založené na komplexních Tauberových teorémech (například Wiener–Ikehara ) jsou často považovány za docela poučné, ale ne elementární, a to navzdory použití Fourierovy analýzy, spíše než komplexní analýzy jako takové. Zde, stejně jako jinde, může být elementární důkaz pro většinu čtenářů delší a obtížnější než neelementární.

Teoretici čísel Paul Erdős a Terence Tao v roce 1985, kdy Erdősovi bylo 72 a Taovi 10.

Teorie čísel má pověst oboru, jehož mnohé výsledky lze říci laikovi. Důkazy těchto výsledků přitom nejsou nijak zvlášť dostupné, zčásti proto, že škála nástrojů, které používají, je v matematice neobvykle široká.

Analytická teorie čísel

Riemann zeta funkce ζ( s ) v komplexní rovině . Barva bodu s udává hodnotu ζ( s ): tmavé barvy označují hodnoty blízké nule a odstín udává argument hodnoty .

Působení modulární skupiny na horní polorovině . Oblast v šedé barvě je standardní základní doménou .

Analytická teorie čísel může být definována

• z hlediska jeho nástrojů, jako je studium celých čísel pomocí nástrojů reálné a komplexní analýzy; nebo
• pokud jde o její obavy, jako je studie v rámci teorie čísel odhadů velikosti a hustoty, na rozdíl od identit.

Některé předměty obecně považované za součást analytické teorie čísel, například teorie síta , jsou lépe pokryty druhou definicí než první: některé z teorie síta například používají málo analýzy, přesto patří do analytické teorie čísel. .

Následují příklady problémů v analytické teorii čísel: teorém o prvočíslech , Goldbachova domněnka (nebo dvojčetná prvočísla nebo Hardy-Littlewoodovy domněnky ), Waringův problém a Riemannova hypotéza . Některé z nejdůležitějších nástrojů analytické teorie čísel jsou kruhová metoda , sítové metody a L-funkce (nebo spíše studium jejich vlastností). Teorie modulárních forem (a obecněji automorfních forem ) také zaujímá stále důležitější místo v sadě nástrojů analytické teorie čísel.

Jeden může klást analytické otázky o algebraických číslech a používat analytické prostředky odpovědět na takové otázky; tak se algebraická a analytická teorie čísel protínají. Například lze definovat prvočísla (zobecnění prvočísel v oboru algebraických čísel) a ptát se, kolik prvočísel existuje do určité velikosti. Tuto otázku lze zodpovědět pomocí zkoumání Dedekindových zeta funkcí , které jsou zobecněním Riemannovy zeta funkce , klíčového analytického objektu u kořenů subjektu. Toto je příklad obecného postupu v analytické teorii čísel: odvozování informace o distribuci posloupnosti (zde prvočíselných ideálů nebo prvočísel) z analytického chování vhodně zkonstruované komplexně hodnotné funkce.

Algebraická teorie čísel

Algebraické číslo je nějaké komplexní číslo, které je řešením nějaké polynomiální rovnice s racionálními koeficienty; například každé řešení ( řekněme) je algebraické číslo. Pole algebraických čísel se také nazývají algebraická číselná pole nebo zkráceně číselná pole . Algebraická teorie čísel studuje algebraická číselná pole. Analytická a algebraická teorie čísel se tedy mohou překrývat a také se překrývají: první je definována svými metodami, druhá svými předměty studia. ${\displaystyle f(x)=0}$${\displaystyle x}$${\displaystyle x^{5}+(11/2)x^{3}-7x^{2}+9=0}$

Dalo by se namítnout, že nejjednodušší druh číselných polí (viz. kvadratická pole) již studoval Gauss, protože diskuse o kvadratických formách v Disquisitiones aritmeticae lze přeformulovat z hlediska ideálů a norem v kvadratických polích. ( Kvadratické pole se skládá ze všech čísel ve tvaru , kde a jsou racionální čísla a je to pevné racionální číslo, jehož druhá odmocnina není racionální.) Ostatně metoda čakravala z 11. století se rovná – v moderních termínech – algoritmu pro nalezení jednotek reálného kvadratického číselného pole. Bhāskara ani Gauss však neznali číselná pole jako taková. ${\displaystyle a+b{\sqrt {d}}}$${\displaystyle a}$${\displaystyle b}$${\displaystyle d}$

Základy předmětu, jak ho známe, byly stanoveny na konci devatenáctého století, kdy byla vyvinuta ideální čísla , teorie ideálů a teorie oceňování ; toto jsou tři doplňkové způsoby, jak se vypořádat s nedostatkem jedinečné faktorizace v algebraických číselných polích. (Například v poli generovaném racionality a , číslo může být faktorizováno jak a ; všechny z , , a jsou neredukovatelné, a tedy v naivním smyslu analogické k prvočíslům mezi celými čísly.) Počáteční impuls pro vývoj ideálních čísel (podle Kummera ) se zdá k pocházeli ze studia vyšších zákonů reciprocity, to znamená zobecnění kvadratické reciprocity . ${\displaystyle {\sqrt {-5}}}$${\displaystyle 6}$${\displaystyle 6=2\cdot 3}$${\displaystyle 6=(1+{\sqrt {-5}})(1-{\sqrt {-5}})}$${\displaystyle 2}$${\displaystyle 3}$${\displaystyle 1+{\sqrt {-5}}}$${\displaystyle 1-{\sqrt {-5}}}$

Číselná pole jsou často studována jako rozšíření menších číselných polí: o poli L se říká, že je rozšířením pole K , pokud L obsahuje K . (Například komplexní čísla C jsou rozšířením reálných čísel R a reálná čísla R jsou rozšířením reálných čísel Q .) Klasifikace možných rozšíření daného číselného pole je obtížný a částečně otevřený problém. Abelovská extenze – tedy extenze L z K taková, že Galoisova grupa Gal( L / K ) z L nad K je abelovská grupa – jsou relativně dobře pochopeny. Jejich klasifikace byla předmětem programu třídní teorie pole , který byl zahájen koncem 19. století (částečně Kroneckerem a Eisensteinem ) a prováděný převážně v letech 1900–1950.

Příkladem aktivní oblasti výzkumu algebraické teorie čísel je teorie Iwasawa . Langlandsův program , jeden z hlavních aktuálních rozsáhlých výzkumných plánů v matematice, je někdy popisován jako pokus zobecnit třídní teorii pole na neabelovská rozšíření číselných polí.

Diofantní geometrie

Ústředním problémem diofantické geometrie je určit, kdy má diofantická rovnice řešení, a pokud ano, kolik. Zaujatý přístup má myslet na řešení rovnice jako na geometrický objekt.

Například rovnice ve dvou proměnných definuje křivku v rovině. Obecněji rovnice nebo systém rovnic ve dvou nebo více proměnných definuje křivku , povrch nebo nějaký jiný takový objekt v n -rozměrném prostoru. V diofantické geometrii se člověk ptá, zda jsou na křivce nebo povrchu nějaké racionální body (body, jejichž všechny souřadnice jsou racionální) nebo integrální body (body, jejichž všechny souřadnice jsou celá čísla). Pokud nějaké takové body existují, dalším krokem je zeptat se, kolik jich je a jak jsou rozděleny. Základní otázkou v tomto směru je, zda je na dané křivce (nebo ploše) konečně nebo nekonečně mnoho racionálních bodů.

V pythagorejské rovnici bychom chtěli studovat její racionální řešení, tedy její řešení taková, že x i y jsou racionální. To je stejné, jako byste požadovali všechna celočíselná řešení pro ; jakékoli řešení druhé rovnice nám dává řešení první rovnice . Je to také stejné jako dotaz na všechny body s racionálními souřadnicemi na křivce popsané pomocí . (Tato křivka je náhodou kruh o poloměru 1 kolem počátku.) ${\displaystyle x^{2}+y^{2}=1,}$${\displaystyle (x,y)}$${\displaystyle a^{2}+b^{2}=c^{2}}$${\displaystyle x=a/c}$${\displaystyle y=b/c}$${\displaystyle x^{2}+y^{2}=1}$

Dva příklady eliptické křivky , tedy křivky rodu 1, která má alespoň jeden racionální bod. (Každý graf lze vidět jako výsek torusu ve čtyřrozměrném prostoru.)

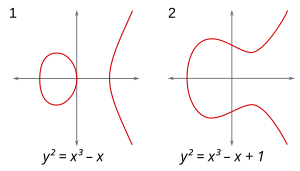
Přeformulování otázek o rovnicích pomocí bodů na křivkách se ukazuje jako šťastné. Konečnost či nekonečnost počtu racionálních nebo celočíselných bodů na algebraické křivce – tedy racionálních nebo celočíselných řešení rovnice , kde je polynom ve dvou proměnných – závisí rozhodujícím způsobem na rodu křivky. Rod může být definován následovně: dovolte, aby proměnné v byly komplexní čísla; pak definuje 2-rozměrný povrch v (projektivním) 4-rozměrném prostoru (protože dvě komplexní proměnné lze rozložit na čtyři reálné proměnné, tedy čtyři rozměry). Počítáme-li počet (koblihových) děr v povrchu; toto číslo nazýváme rodem . Ostatní geometrické pojmy se ukazují být stejně zásadní. ${\displaystyle f(x,y)=0}$${\displaystyle f}$${\displaystyle f(x,y)=0}$${\displaystyle f(x,y)=0}$${\displaystyle f(x,y)=0}$

Je zde také úzce propojená oblast diofantických aproximací : dané číslo a zjištění, jak dobře je lze aproximovat racionálními úvahami. (Hledáme aproximace, které jsou dobré vzhledem k množství prostoru, který je potřeba k zápisu racionálního: call (s ) dobrou aproximací k if , kde je velké.) Tato otázka je zvláště zajímavá, pokud je algebraické číslo. Pokud je nelze dobře aproximovat, pak některé rovnice nemají celočíselná nebo racionální řešení. Kromě toho se několik konceptů (zejména výšky ) ukazuje jako kritických jak v diofantické geometrii, tak ve studiu diofantických aproximací. Tato otázka je také zvláštního zájmu v transcendentální teorii čísel : jestliže číslo může být lépe aproximované než nějaké algebraické číslo, pak to je transcendentální číslo . Právě tímto argumentem se ukázalo , že π a e jsou transcendentální.${\displaystyle x}$${\displaystyle a/q}$${\displaystyle \gcd(a,q)=1}$${\displaystyle x}$${\displaystyle |xa/q|<{\frac {1}{q^{c}}}}$${\displaystyle c}$${\displaystyle x}$${\displaystyle x}$

Diofantická geometrie by neměla být zaměňována s geometrií čísel , což je sbírka grafických metod pro zodpovězení určitých otázek v algebraické teorii čísel. Aritmetická geometrie , nicméně, je současný termín pro hodně stejnou doménu jako ta krytá termínem Diophantine geometrie . Termín aritmetická geometrie je pravděpodobně používán nejvíce často, když jeden přeje si zdůraznit spojení s moderní algebraickou geometrií (jako v, například, Faltingsův teorém ) spíše než k technikám v Diophantine přiblížení.

Další podpole

Níže uvedené oblasti nepocházejí z dřívější poloviny dvacátého století, i když jsou založeny na starším materiálu. Například, jak je vysvětleno níže, záležitost algoritmů v teorii čísel je velmi stará, v jistém smyslu starší než koncept důkazu; přitom moderní studium vyčíslitelnosti pochází až z 30. a 40. let a teorie výpočetní složitosti ze 70. let.

Pravděpodobnostní teorie čísel

Hodně z pravděpodobnostní teorie čísel může být viděno jako důležitý zvláštní případ studia proměnných, které jsou téměř, ale ne docela, vzájemně nezávislé . Například událost, že náhodné celé číslo mezi jedním a milionem je dělitelné dvěma, a událost, že je dělitelné třemi, jsou téměř nezávislé, ale ne tak docela.

Někdy se říká, že pravděpodobnostní kombinatorika využívá skutečnosti, že cokoli se stane s pravděpodobností větší, než se někdy musí stát; se stejnou spravedlností lze říci, že mnoho aplikací pravděpodobnostní teorie čísel závisí na skutečnosti, že cokoli je neobvyklé, musí být vzácné. Pokud lze ukázat, že určité algebraické objekty (řekněme racionální nebo celočíselná řešení určitých rovnic) jsou na konci určitých rozumně definovaných distribucí, vyplývá z toho, že jich musí být málo; toto je velmi konkrétní nepravděpodobnostní tvrzení vyplývající z pravděpodobnostního. ${\displaystyle 0}$

Občas nerigorózní, pravděpodobnostní přístup vede k řadě heuristických algoritmů a otevřeným problémům, zejména Cramérově domněnce .

Aritmetická kombinatorika

Začneme-li od poměrně "tlusté" nekonečné množiny , obsahuje mnoho prvků v aritmetickém postupu: , , řekněme? Mělo by být možné zapsat velká celá čísla jako součty prvků ? ${\displaystyle A}$${\displaystyle a}$${\displaystyle a+b,a+2b,a+3b,\ldots ,a+10b}$${\displaystyle A}$

Tyto otázky jsou charakteristické pro aritmickou kombinatoriku . Toto je v současnosti splývající pole; to zahrnuje aditivní číselnou teorii (která se zabývá jistými velmi specifickými soubory aritmetického významu, takový jako prvočísla nebo čtverce) a, pravděpodobně, některá ta geometrie čísel , spolu s nějakým rychle se vyvíjejícím novým materiálem. Jeho zaměření na otázky růstu a distribuce částečně odpovídá za jeho rozvíjející se vazby s ergodickou teorií , teorií konečných grup , teorií modelů a dalšími obory. Používá se také termín aditivní kombinatorika ; studované množiny však nemusí být množiny celých čísel, ale spíše podmnožiny nekomutativních grup , pro které se tradičně používá symbol násobení, nikoli symbol sčítání; mohou být také podskupinami prstenců , v takovém případě lze růst a · porovnávat. ${\displaystyle A}$${\displaystyle A}$${\displaystyle A+A}$${\displaystyle A}$${\displaystyle A}$

Výpočetní teorie čísel

Lehmerovo síto , primitivní digitální počítač používaný k nalezení prvočísel a řešení jednoduchých diofantických rovnic .

Zatímco slovo algoritmus se vrací pouze k některým čtenářům al-Khwārizmī , pečlivé popisy metod řešení jsou starší než důkazy: takové metody (tj. algoritmy) jsou staré jako jakákoli známá matematika – starověká egyptská, babylonská, védská, čínská — zatímco důkazy se objevily pouze u Řeků klasického období.

První případ je případ toho, co nyní nazýváme Euklidovský algoritmus . Ve své základní podobě (jmenovitě jako algoritmus pro výpočet největšího společného dělitele ) se objevuje jako Tvrzení 2 Knihy VII v Prvcích spolu s důkazem správnosti. Avšak ve formě, která se často používá v teorii čísel (jmenovitě jako algoritmus pro hledání celočíselných řešení rovnice , nebo, což je totéž, pro hledání veličin, jejichž existenci zajišťuje čínská věta o zbytku ) se poprvé objevuje v dílech Áryabhaṭy (5.–6. století n. l.) jako algoritmus zvaný kuṭṭaka („pulveriser“), bez důkazu o správnosti. ${\displaystyle ax+by=c}$

Existují dvě hlavní otázky: "Můžeme to spočítat?" a "Můžeme to spočítat rychle?" Kdokoli může otestovat, zda je číslo prvočíslo, nebo pokud není, rozdělit ho na prvočísla; dělat to rychle je jiná věc. Nyní známe rychlé algoritmy pro testování primality , ale přes mnoho práce (teoretické i praktické) neexistuje žádný skutečně rychlý algoritmus pro faktoring.

Obtížnost výpočtu může být užitečná: moderní protokoly pro šifrování zpráv (například RSA ) závisí na funkcích, které jsou známy všem, ale jejichž inverzní křivky zná pouze několik vyvolených a jejich zjištění by trvalo příliš dlouho. ven na vlastní pěst. Tyto funkce mohou být například takové, že jejich převrácené hodnoty lze vypočítat pouze v případě, že určitá velká celá čísla jsou faktorizována. I když je známo mnoho obtížných výpočetních problémů mimo teorii čísel, většina pracovních šifrovacích protokolů je v dnešní době založena na obtížnosti několika číselných teoretických problémů.

Některé věci nemusí být vůbec vyčíslitelné; ve skutečnosti to lze v některých případech dokázat. Například v roce 1970 bylo jako řešení Hilbertova 10. problému prokázáno, že neexistuje žádný Turingův stroj , který by dokázal vyřešit všechny diofantické rovnice. Konkrétně to znamená, že vzhledem k vyčíslitelnému souboru axiomů existují diofantické rovnice, pro které neexistuje žádný důkaz, počínaje axiomy, zda soubor rovnic má nebo nemá celočíselná řešení. (Zbytečně bychom mluvili o diofantických rovnicích, pro které neexistují celočíselná řešení, protože vzhledem k diofantické rovnici s alespoň jedním řešením poskytuje řešení samo o sobě důkaz skutečnosti, že řešení existuje. Nemůžeme dokázat, že konkrétní diofantina rovnice je tohoto druhu, protože by to znamenalo, že nemá řešení.)

Aplikace

Teoretik čísel Leonard Dickson (1874–1954) řekl: „Díky bohu, že teorie čísel není poskvrněna žádnou aplikací“. Takový pohled již není aplikovatelný na teorii čísel. V roce 1974 Donald Knuth řekl „...prakticky každý teorém v elementární teorii čísel vzniká přirozeným, motivovaným způsobem v souvislosti s problémem přimět počítače k ​​vysokorychlostním numerickým výpočtům“. Základní teorie čísel se vyučuje v diskrétních matematických kurzech pro počítačové vědce ; na druhé straně, teorie čísel má také aplikace pro spojitý v numerické analýze . Kromě dobře známých aplikací pro kryptografii existují také aplikace v mnoha dalších oblastech matematiky.

Ceny

Americká matematická společnost uděluje Coleovu cenu v teorii čísel . Teorie čísel je navíc jednou ze tří matematických podoborů oceněných Fermatovou cenou .

Viz také

• Algebraické funkční pole
• Konečné pole
• p-adické číslo

Poznámky

Reference

Prameny

• Tento článek zahrnuje materiál z článku Citizendium „ Teorie čísel “, který je licencován pod licencí Creative Commons Attribution-ShareAlike 3.0 Unported License , ale nikoli pod licencí GFDL .

Další čtení

Dva z nejpopulárnějších úvodů k tématu jsou:

• GH Hardy ; EM Wright (2008) [1938]. Úvod do teorie čísel (rev. DR Heath-Brown a JH Silverman, 6. vydání). Oxford University Press . ISBN 978-0-19-921986-5. Získáno 2016-03-02 .
• Vinogradov, IM (2003) [1954]. Elements of Number Theory (reprint vydání z roku 1954). Mineola, NY: Dover Publications.

Kniha Hardyho a Wrighta je obsáhlou klasikou, i když její srozumitelnost někdy trpí kvůli tomu, že autoři trvají na elementárních metodách ( Apostol nd ). Hlavní přitažlivost Vinogradova spočívá v jeho souboru problémů, které rychle vedou k vlastním výzkumným zájmům Vinogradova; samotný text je velmi základní a téměř minimální. Další populární první úvody jsou:

• Ivan M. Niven ; Herbert S. Zuckerman; Hugh L. Montgomery (2008) [1960]. Úvod do teorie čísel (dotisk 5. vydání 1991, ed.). John Wiley & Sons . ISBN 978-81-265-1811-1. Získáno 28. 02. 2016 .
• Kenneth H. Rosen (2010). Elementární teorie čísel (6. vydání). Pearsonovo vzdělání . ISBN 978-0-321-71775-7. Získáno 28. 02. 2016 .

Mezi oblíbené možnosti pro druhou učebnici patří:

• Borevič, AI ; Shafarevič, Igor R. (1966). Teorie čísel . Čistá a aplikovaná matematika. sv. 20. Boston, MA: Academic Press . ISBN 978-0-12-117850-5. MR  0195803 .
• Serre, Jean-Pierre (1996) [1973]. Kurz aritmetiky . Absolventské texty z matematiky . sv. 7. Springer. ISBN 978-0-387-90040-7.

externí odkazy

• Média související s teorií čísel na Wikimedia Commons
• Heslo teorie čísel v Encyklopedii matematiky
• Web teorie čísel