Octonion - Octonion

Octonions
Octonions
Symbol
Typ	Hyperkomplexní algebra
Jednotky	e 0 , ..., e 7
Multiplikativní identita	e 0
Hlavní vlastnosti	Nekomutativní ; non-asociativní
Běžné systémy
	Méně běžné systémy Octonions ( ) Sedenions ( )

V matematice se octonions jsou normed rozdělení algebra nad reálnými čísly , druh hyperkomplexní číselné soustavy . Oktoniony jsou obvykle reprezentovány velkým písmenem O, tučným písmem $O$ nebo tučně napsaným na tabuli . Octonions mají osm dimenzí ; dvojnásobný počet rozměrů čtveřic , z nichž jsou rozšířením. Jsou nekomutativní a neasociativní , ale uspokojují slabší formu asociativity; totiž jsou alternativní . Jsou také asociativní k moci . ${\ displaystyle \ mathbb {O}}$

Oktonioni nejsou tak známí jako kvaterniony a komplexní čísla , která jsou mnohem více studována a používána. Octonions se týkají výjimečných struktur v matematice, mezi nimi výjimečných Lieových skupin . Octonions mají aplikace v oblastech, jako je teorie strun , speciální relativita a kvantová logika . Aplikací konstrukce Cayley – Dickson na octoniony vznikají sedeniony .

Dějiny

Oktoniony byly objeveny v roce 1843 Johnem T. Gravesem , inspirovaným objevem jeho kvarterů jeho přítelem Williamem Rowanem Hamiltonem . Graves nazval svůj objev „oktávami“ a zmínil se o nich v dopise Hamiltonovi ze dne 16. prosince 1843. Svůj výsledek poprvé publikoval o něco později než článek Arthura Cayleyho . Oktoniony byly objeveny nezávisle Cayleyem a jsou někdy označovány jako „Cayleyova čísla“ nebo „Cayleyova algebra“. Hamilton popsal ranou historii Gravesova objevu.

Definice

Oktoniony lze považovat za oktety (nebo 8-tice) skutečných čísel. Každý oktonion je skutečná lineární kombinace z jednotky octonions :

{\ Displaystyle \ {e_ {0}, e_ {1}, e_ {2}, e_ {3}, e_ {4}, e_ {5}, e_ {6}, e_ {7} \},}

kde $e 0$ je skalární nebo skutečný prvek; může být identifikováno skutečným číslem 1. To znamená, že každý octonion $x$ může být zapsán ve formě

{\ displaystyle x = x_ {0} e_ {0}+x_ {1} e_ {1}+x_ {2} e_ {2}+x_ {3} e_ {3}+x_ {4} e_ {4}+ x_ {5} e_ {5}+x_ {6} e_ {6}+x_ {7} e_ {7}, \,}

se skutečnými koeficienty $x i$ .

Sčítání a odčítání oktonionů se provádí sčítáním a odčítáním odpovídajících členů, a tedy jejich koeficientů, jako kvaternionů. Násobení je složitější. Násobení je distribuční přes sčítání, takže součin dvou oktonů lze vypočítat součtem součinů všech výrazů, opět jako čtveřice. Součin každé dvojice výrazů může být dán vynásobením koeficientů a multiplikační tabulkou jednotkových oktonů, jako je tento (kvůli Cayley, 1845 a Graves, 1843):

${\ displaystyle e_ {i} e_ {j}}$		${\ displaystyle e_ {j}}$
${\ displaystyle e_ {i} e_ {j}}$		${\ displaystyle e_ {0}}$	${\ displaystyle e_ {1}}$	${\ displaystyle e_ {2}}$	${\ displaystyle e_ {3}}$	${\ displaystyle e_ {4}}$	${\ displaystyle e_ {5}}$	${\ displaystyle e_ {6}}$	${\ displaystyle e_ {7}}$
${\ displaystyle e_ {i}}$	${\ displaystyle e_ {0}}$	${\ displaystyle e_ {0}}$	${\ displaystyle e_ {1}}$	${\ displaystyle e_ {2}}$	${\ displaystyle e_ {3}}$	${\ displaystyle e_ {4}}$	${\ displaystyle e_ {5}}$	${\ displaystyle e_ {6}}$	${\ displaystyle e_ {7}}$
	${\ displaystyle e_ {1}}$	${\ displaystyle e_ {1}}$	${\ displaystyle -e_ {0}}$	${\ displaystyle e_ {3}}$	${\ displaystyle -e_ {2}}$	${\ displaystyle e_ {5}}$	${\ displaystyle -e_ {4}}$	${\ displaystyle -e_ {7}}$	${\ displaystyle e_ {6}}$
	${\ displaystyle e_ {2}}$	${\ displaystyle e_ {2}}$	${\ displaystyle -e_ {3}}$	${\ displaystyle -e_ {0}}$	${\ displaystyle e_ {1}}$	${\ displaystyle e_ {6}}$	${\ displaystyle e_ {7}}$	${\ displaystyle -e_ {4}}$	${\ displaystyle -e_ {5}}$
	${\ displaystyle e_ {3}}$	${\ displaystyle e_ {3}}$	${\ displaystyle e_ {2}}$	${\ displaystyle -e_ {1}}$	${\ displaystyle -e_ {0}}$	${\ displaystyle e_ {7}}$	${\ displaystyle -e_ {6}}$	${\ displaystyle e_ {5}}$	${\ displaystyle -e_ {4}}$
	${\ displaystyle e_ {4}}$	${\ displaystyle e_ {4}}$	${\ displaystyle -e_ {5}}$	${\ displaystyle -e_ {6}}$	${\ displaystyle -e_ {7}}$	${\ displaystyle -e_ {0}}$	${\ displaystyle e_ {1}}$	${\ displaystyle e_ {2}}$	${\ displaystyle e_ {3}}$
	${\ displaystyle e_ {5}}$	${\ displaystyle e_ {5}}$	${\ displaystyle e_ {4}}$	${\ displaystyle -e_ {7}}$	${\ displaystyle e_ {6}}$	${\ displaystyle -e_ {1}}$	${\ displaystyle -e_ {0}}$	${\ displaystyle -e_ {3}}$	${\ displaystyle e_ {2}}$
	${\ displaystyle e_ {6}}$	${\ displaystyle e_ {6}}$	${\ displaystyle e_ {7}}$	${\ displaystyle e_ {4}}$	${\ displaystyle -e_ {5}}$	${\ displaystyle -e_ {2}}$	${\ displaystyle e_ {3}}$	${\ displaystyle -e_ {0}}$	${\ displaystyle -e_ {1}}$
	${\ displaystyle e_ {7}}$	${\ displaystyle e_ {7}}$	${\ displaystyle -e_ {6}}$	${\ displaystyle e_ {5}}$	${\ displaystyle e_ {4}}$	${\ displaystyle -e_ {3}}$	${\ displaystyle -e_ {2}}$	${\ displaystyle e_ {1}}$	${\ displaystyle -e_ {0}}$

Většina off-diagonálních prvků tabulky je antisymetrická, což z ní činí téměř šikmou symetrickou matici kromě prvků na hlavní diagonále, stejně jako řádku a sloupce, pro které $e 0$ je operand.

Tabulku lze shrnout následovně:

{\ Displaystyle e_ {i} e_ {j} = {\ begin {cases} e_ {j}, & {\ text {if}} i = 0 \\ e_ {i}, & {\ text {if}} j = 0 \\-\ delta _ {ij} e_ {0}+\ varepsilon _ {ijk} e_ {k}, & {\ text {else}} \ end {cases}}}

kde $δ ij$ je Kroneckerova delta (rovná 1 právě tehdy, když $i = j$ ), a $ε ijk$ je zcela antisymetrický tenzor s hodnotou 1, když $ijk = 123, 145, 176, 246, 257, 347, 365$ .

Výše uvedená definice však není jedinečná; je to jen jedna ze 480 možných definic pro násobení oktonů s $e 0 = 1$ . Ostatní lze získat permutací a změnou znaků nekalárních bazických prvků ${e 1, e 2, e 3, e 4, e 5, e 6, e 7}$ . 480 různých algeber je izomorfních a jen zřídka je třeba zvážit, jaké konkrétní pravidlo násobení se používá.

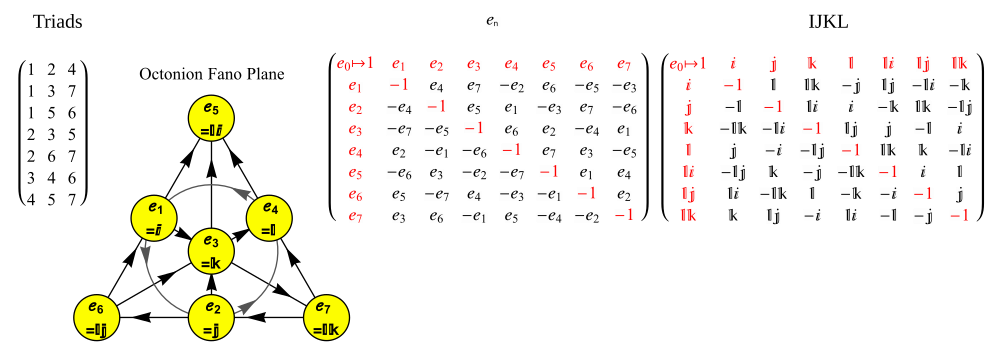
Každá z těchto 480 definic je invariantní až do znaků pod nějakým 7-cyklem bodů (1234567) a pro každý 7-cyklus existují čtyři definice, které se liší znaménky a obrácením pořadí. Běžnou volbou je použít invariant definice pod 7 cykly (1234567) s $e 1 e 2 = e 4$ -pomocí trojúhelníkového multiplikačního diagramu nebo Fano roviny níže, která také ukazuje seřazený seznam 124 založených na 7 cyklech triád a jeho přidružené multiplikační matice ve formátu $e n$ i IJKL.

Octonionové triády, Fano rovina a multiplikační matice

Variace tohoto někdy používaného je označit prvky základu prvky $\infty$ , 0, 1, 2, ..., 6 projektivní přímky přes konečné pole řádu 7. Násobení je pak dáno $e \infty = 1$ a $e 1 e 2 = e 4$ , a všechny výrazy získané z toho přidáním konstanty ( modulo 7) ke všem indexům: jinými slovy pomocí sedmi trojic (124) (235) (346) (450) ( 561) (602) (013). Toto jsou nenulová kódová slova kvadratického zbytkového kódu délky 7 v Galoisově poli dvou prvků, $GF (2)$ . Existuje symetrie řádu 7 daná přidáním konstantního mod 7 ke všem dolním indexům a také symetrie řádu 3 daná vynásobením všech indexů jedním z kvadratických zbytků 1, 2, 4 mod 7.

Násobící tabulku pro geometrickou algebru podpisu $(----)$ lze vyjádřit následujícími 7 kvartérními trojicemi (vynecháním prvku identity):

(I, j, k), (i, J, k), (i, j, K), (I, J, K), (* I, i, m), (* J, j, m), (* K, k, m)

ve kterých jsou malá písmena vektory a velká písmena bivektory a $* = mijk$ (což je $Hodgeův$ hvězdný operátor ). Pokud je $*$ nucen být roven identitě, pak násobení přestává být asociativní, ale $*$ může být odstraněno z multiplikační tabulky, což má za následek oktonionovou multiplikační tabulku.

Při zachování asociativní $* = mijk,$ a tedy $neredukování$ 4-dimenzionální geometrické algebry na oktonionovou, lze celou multiplikační tabulku odvodit z rovnice pro $*$ . Zvažte gama matice . Vzorec definující pátou matici gama ukazuje, že jde o $*$ čtyřrozměrné geometrické algebry gama matic.

Cayley – Dicksonova konstrukce

Systematičtější způsob definování octonionů je prostřednictvím konstrukce Cayley – Dickson. Stejně jako kvaterniony lze definovat jako páry komplexních čísel, oktoniony lze definovat jako páry quaternionů. Sčítání je definováno párově. Součin dvou párů čtveřic $(a, b)$ a $(c, d)$ je definován vztahem

{\ Displaystyle (a, b) (c, d) = (ac-d^{*} b, da+bc^{*}),}

kde $z *$ označuje konjugát čtveřice $z$ . Tato definice je ekvivalentní té, která je uvedena výše, když je s jednotkami identifikováno osm jednotkových octonionů

(1, 0), (i, 0), (j, 0), (k, 0), (0, 1), (0, i), (0, j), (0, k)

Fano letadlo mnemotechnická pomůcka

Mnemotechnická pomůcka pro produkty jednotkových oktonů.

3D mnemotechnická vizualizace ukazující 7 triád jako hyperplanes přes skutečný (

e 0

) vrchol výše uvedeného příkladu octonionu.

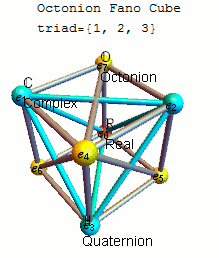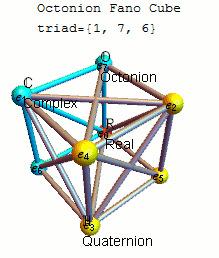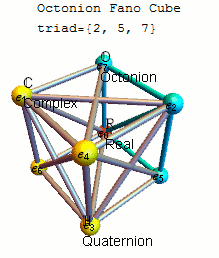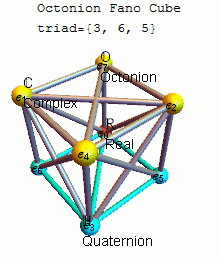
Vhodným mnemotechnická pomůcka pro zapamatování produkty jednotkových octonions je dána na obrázku, který představuje násobilku Cayley a Graves. Tento diagram se sedmi body a sedmi přímkami (kružnice procházející 1, 2 a 3 je považována za přímku) se nazývá Fano rovina . Čáry jsou směrové. Sedm bodů odpovídá sedmi standardním základním prvkům $Im (O)$ (viz definice níže ). Každý pár odlišných bodů leží na jedinečné čáře a každá čára prochází přesně třemi body.

Nechť $(a, b, c)$ je uspořádaná trojice bodů ležících na dané přímce s pořadím určeným směrem šipky. Pak je násobení dáno vztahem

ab = c

a

ba = - c

společně s cyklickými permutacemi . Tato pravidla společně s

1 je multiplikativní identita,
$E 2 i = -1$ pro každý bod v diagramu

zcela definuje multiplikativní strukturu octonionů. Každý ze sedmi linek generuje podalgebry z $O$ izomorfní k čtveřic $H$ .

Konjugát, norma a inverze

Konjugát z oktonion

{\ Displaystyle x = x_ {0} \, e_ {0}+x_ {1} \, e_ {1}+x_ {2} \, e_ {2}+x_ {3} \, e_ {3}+x_ {4} \, e_ {4}+x_ {5} \, e_ {5}+x_ {6} \, e_ {6}+x_ {7} \, e_ {7}}

je dána

{\ Displaystyle x^{*} = x_ {0} \, e_ {0} -x_ {1} \, e_ {1} -x_ {2} \, e_ {2} -x_ {3} \, e_ { 3} -x_ {4} \, e_ {4} -x_ {5} \, e_ {5} -x_ {6} \, e_ {6} -x_ {7} \, e_ {7}.}

Konjugace je involuce z $O$ a splňuje $(xy) * = y * x *$ (všimněte si změny v pořadí).

Reálná část z $x$ je dána vztahem

{\ displaystyle {\ frac {x+x^{*}} {2}} = x_ {0} \, e_ {0}}

a imaginární část by

{\ displaystyle {\ frac {xx^{*}} {2}} = x_ {1} \, e_ {1}+x_ {2} \, e_ {2}+x_ {3} \, e_ {3} +x_ {4} \, e_ {4}+x_ {5} \, e_ {5}+x_ {6} \, e_ {6}+x_ {7} \, e_ {7}.}

Soubor všech čistě imaginární octonions rozpětí 7- rozměrovou podprostoru z $O$ , označil $Im (O)$ .

Konjugace octonionů splňuje rovnici

{\ Displaystyle x^{*} =-{\ tfrac {1} {6}} {\ bigl (} x+(e_ {1} x) e_ {1}+(e_ {2} x) e_ {2}+ (e_ {3} x) e_ {3}+(e_ {4} x) e_ {4}+(e_ {5} x) e_ {5}+(e_ {6} x) e_ {6}+(e_ {7} x) e_ {7} {\ bigr)}.}

Součin oktonionu s jeho konjugátem, $x * x = xx *$ , je vždy nezáporné reálné číslo:

{\ Displaystyle x^{*} x = x_ {0}^{2}+x_ {1}^{2}+x_ {2}^{2}+x_ {3}^{2}+x_ {4} ^{2}+x_ {5}^{2}+x_ {6}^{2}+x_ {7}^{2}.}

Pomocí toho lze definovat normu oktonionu, jako

{\ Displaystyle \ | x \ | = {\ sqrt {x^{*} x}}.}

Tato norma souhlasí se standardní 8-dimenzionální euklidovskou normou na $R 8$ .

Existence normy o $O$ implikuje existenci inverzí pro každý nenulový prvek $kyslíku$ . Převrácená hodnota $x \neq 0$ , což je jedinečný oktonion $x -1$ splňující $xx -1 = x -1 x = 1$ , je dána vztahem

{\ Displaystyle x^{-1} = {\ frac {x^{*}} {\ | x \ |^{2}}}.}

Vlastnosti

Octonionic multiplikace není ani komutativní :

e i e j = -e j e i \neq e j e i

pokud

i

,

j

jsou odlišné a nenulové,

ani asociativní :

(e i e j) e k = -e i (e j e k) \neq e i (e j e k)

pokud

i

,

j

,

k

jsou odlišné, nenulové a

e i e j \neq \pm e k

.

Oktoniové uspokojují slabší formu asociativity: jsou alternativní. To znamená, že subalgebra generovaná libovolnými dvěma prvky je asociativní. Ve skutečnosti lze ukázat, že subalgebra generovaná jakýmikoli dvěma prvky $O$ je izomorfní k $R$ , $C$ nebo $H$ , z nichž všechny jsou asociativní. Vzhledem k jejich non-asociativitě, octonions nemůže být zastoupen podalgebry části matrice kruhu přes , na rozdíl od reálných čísel, komplexní čísla a čtveřice. ${\ displaystyle \ mathbb {R}}$

Oktoniové si zachovávají jednu důležitou vlastnost sdílenou $R$ , $C$ a $H$ : norma na $O$ splňuje

{\ Displaystyle \ | xy \ | = \ | x \ | \ | y \ |.}

Tato rovnice znamená, že oktoni tvoří algebru kompozice . Algebry vyšší dimenze definované Cayley-Dicksonovou konstrukcí (počínaje sedeniony ) všechny tuto vlastnost nesplňují. Všichni mají nulové dělitele .

Existují širší číselné systémy, které mají multiplikativní modul (například 16dimenzionální kónické sedimenty). Jejich modul je definován odlišně od jejich normy a také obsahují nulové dělitele.

Jak ukazuje Hurwitz , $R$ , $C$ , $H$ a $O$ jsou jedinou normovanou divizní algebrou nad skutečnými čísly. Tyto čtyři algebry také tvoří jedinou alternativní, konečně dimenzionální dělení algeber na skutečná čísla ( až do izomorfismu).

Protože nejsou asociativní, nenulové prvky $O$ netvoří skupinu . Vytvářejí však smyčku , konkrétně smyčku Moufang .

Komutátor a křížový produkt

Komutátor dvou octonions $x$ a $y$ je dána vztahem

{\ Displaystyle [x, y] = xy-yx.}

To je antisymetrické a imaginární. Pokud je považován pouze za produkt v imaginárním podprostoru $Im (O)$ , definuje produkt v tomto prostoru, sedmidimenzionální křížový produkt , daný

{\ Displaystyle x \ times y = {\ tfrac {1} {2}} (xy-yx).}

Jako produkt kříže ve třech rozměrech je to vektor kolmý k $x$ a $y$ s velikostí

{\ Displaystyle \ | x \ times y \ | = \ | x \ | \ | y \ | \ sin \ theta.}

Ale stejně jako produkt octonion není jednoznačně definován. Místo toho existuje mnoho různých křížových produktů, každý závisí na výběru oktonionového produktu.

Automorfismy

Automorphism , , z octonions je invertible lineární transformace z $O$ , který splňuje

{\ Displaystyle A (xy) = A (x) A (y).}

Soubor všech automorfismů $O$ tvoří skupinu s názvem $G 2$ . Skupina $G 2$ je potom spojen , kompaktní , skutečný Lie skupina rozměru 14. Tato skupina je nejmenší z výjimečných Lieových skupin a je izomorfní v podskupině z $rotace (7)$ , která chrání jakékoliv zvolené konkrétní vektor v jeho 8-rozměrný skutečné zastoupení spinoru. Skupina $Spin (7)$ je zase podskupinou níže popsané skupiny izotopů.

Viz také : $PSL (2,7)$ - skupina automorfismu letadla Fano.

Izotopie

Isotopy z algebry je trojice bijective lineárních map $s$ , $b$ , $c$ tak, že v případě, $xy = z$ pak $($ $x$ $)$ $b$ $($ $y$ $) =$ $c$ $($ $z$ $)$ . Pro $a$ $=$ $b$ $=$ $c$ je to stejné jako automorfismus. Skupina izotopů algebry je skupina všech izotopií, která obsahuje skupinu automorfismů jako podskupinu.

Izotopy skupina octonions je skupina $Spin 8 (R)$ , přičemž $a$ , $b$ , $c$ působí jako tři 8-dimenzionální reprezentace. Podskupina prvků, kde $c$ opravuje identitu, je podskupina $Spin 7 (R)$ a podskupina, kde $a$ , $b$ , $c$ všechny opravují identitu, je skupina automorfismu $G 2$ .

Aplikace

Oktoniové hrají významnou roli při klasifikaci a konstrukci dalších matematických entit. Například výjimečná Lieova skupina $G 2$ je automorfistická skupina octonionů a další výjimečné Lieovy skupiny $F 4$ , $E 6$ , $E 7$ a $E 8$ lze chápat jako izometrie určitých projektivních rovin definovaných pomocí octonionů. Sada samostatně nastavitelných 3 × 3 oktonionických matic , vybavených symetrickým součinem matice, definuje Albertovu algebru . V diskrétní matematice poskytují octoniony elementární odvození Leechovy mřížky , a proto jsou v těsném spojení se sporadickými jednoduchými skupinami .

Aplikace octonionů na fyziku byly do značné míry domněnky. Například v 70. letech 20. století byly učiněny pokusy porozumět kvarkům prostřednictvím oktonionického Hilbertova prostoru . Je známo, že octoniony a skutečnost, že mohou existovat pouze čtyři normované divizní algebry, se týká rozměrů časoprostoru, ve kterých lze konstruovat supersymetrické teorie kvantového pole . Také byly provedeny pokusy k získání standardní model fyziky elementárních částic od octonionic konstrukcí, například pomocí „Dixon algebry“ $C \otimes H \otimes O$ .

Octonions také vznikly při studiu entropie černé díry a kvantové informační vědy .

Octonions were used in solutions to the hand eye calibration problem in robotics .

Hluboké octonionové sítě poskytují způsob efektivního a kompaktního vyjádření v aplikacích strojového učení.

Integrální octoniony

Existuje několik přirozených způsobů, jak zvolit integrální formu octonionů. Nejjednodušší je vzít octoniony, jejichž souřadnice jsou celá čísla . To dává neasociativní algebru nad celými čísly nazývanými Gravesian octonions. Nejde však o maximální řád (ve smyslu prstencové teorie); obsahuje přesně sedm maximálních řádů. Těchto sedm maximálních řádů je za automorfismů ekvivalentních. Fráze „integrální octonioni“ obvykle označuje fixní volbu jednoho z těchto sedmi řádů.

Tyto maximální objednávky zkonstruovali Kirmse (1925) , Dickson a Bruck následovně. Osm základních vektorů označte body projektivní čáry nad polem se sedmi prvky. Nejprve vytvořte „Kirmse integer“: skládají se z octonionů, jejichž souřadnice jsou celá nebo poloviční, a poloviční celá čísla (tj. Poloviny lichých celých čísel) na jedné ze 16 sad

\emptyset (\infty124) (\infty235) (\infty346) (\infty450) (\infty561) (\infty602) (\infty013) (\infty0123456) (0356) (1460) (2501) (3612) (4023) (5134 ) (6245)

rozšířeného kvadratického zbytkového kódu délky 8 přes pole dvou prvků, dané vztahem $\emptyset$ , $(\infty124)$ a jeho obrazy při přidání konstantní modulo 7, a komplementy těchto osmi sad. Poté přepněte nekonečno a libovolnou další souřadnici; tato operace vytvoří bijekci celých čísel Kirmse na jinou sadu, což je maximální pořadí. Existuje sedm způsobů, jak toho dosáhnout, což dává sedm maximálních řádů, které jsou všechny ekvivalentní při cyklických permutacích sedmi souřadnic 0123456. (Kirmse nesprávně tvrdil, že Kirmseova celá čísla také tvoří maximální řád, takže si myslel, že existuje osm maximálních řádů, nikoli sedm, ale jak zdůraznil Coxeter (1946) , nejsou uzavřeny při násobení; k této chybě dochází v několika publikovaných článcích.)

Celá Kirmseova čísla a sedm maximálních řádů jsou izometrické k mřížce $E 8,$ jejíž měřítko je změněno faktorem 1 / √ 2 . V každém z těchto řádů je zejména 240 prvků minimální nenulové normy 1, které tvoří smyčku Moufang řádu 240.

Integrální oktoniony mají vlastnost „dělení se zbytkem“: vzhledem k integrálním octonionům $a$ a $b \neq 0$ můžeme najít $q$ a $r$ s $a = qb + r$ , kde zbytek $r$ má normu menší než $b$ .

V integrálních octonionech jsou všechny levé ideály a pravé ideály 2stranné ideály a jediné 2stranné ideály jsou hlavní ideály $nO,$ kde $n$ je nezáporné celé číslo.

Integrální octoniony mají verzi faktorizace na prvočísla, ačkoli to není jednoduché uvést, protože octonions nejsou asociativní, takže součin octonions závisí na pořadí, ve kterém člověk dělá produkty. Neredukovatelné integrální oktoniony jsou přesně ty, které mají primární normu, a každý integrální oktonion lze zapsat jako produkt neredukovatelných oktonionů. Přesněji integrální oktonion normy $mn$ lze zapsat jako součin integrálních oktonionů norem $m$ a $n$ .

Automorphism skupina integrálních octonions je skupina $G 2 (F 2),$ z řádu 12,096, který má jednoduchou podskupina indexu 2 izomorfní k ucelené skupiny $2 A 2 (3 2)$ . Skupina izotopů integrálních octonionů je dokonalým dvojitým krytem skupiny rotací mřížky $E 8$ .

Viz také

Poznámky

Reference

Baez, John C. (2002). "Octonions" . Bulletin Americké matematické společnosti . 39 (2): 145–205. arXiv : matematika/0105155 . doi : 10,1090/S0273-0979-01-00934-X . ISSN 0273-0979 . MR 1886087 . S2CID 586512 .
Baez, John C. (2005). „Errata pro Octonions “ (PDF) . Bulletin Americké matematické společnosti . 42 (2): 213–214. doi : 10,1090/S0273-0979-05-01052-9 .
Conway, John Horton ; Smith, Derek A. (2003), On Quaternions and Octonions: their Geometry, Arithmetic, and Symmetry , AK Peters, Ltd., ISBN 1-56881-134-9, Zbl 1098.17001. ( Recenze ).
Coxeter, HSM (1946), „Integral Cayley numbers.“, Duke Math. J. , 13 (4): 561–578, doi : 10,1215/s0012-7094-46-01347-6 , MR 0019111
Dixon, Geoffrey M. (1994), Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics , Kluvwer Academic Publishers, ISBN 0-7923-2890-6
Freudenthal, Hans (1985) [1951], "Oktaven, Ausnahmegruppen und Oktavengeometrie", Geom. Dedicata , 19 (1): 7–63, doi : 10,1007/BF00233101 , MR 0797151 , S2CID 121496094
Graves (1845), „O spojení mezi obecnou teorií normálních párů a teorií úplných kvadratických funkcí dvou proměnných“ , Phil. Mag. , 26 : 315–320, doi : 10,1080/14786444508645136
Kirmse (1924), „Über die Darstellbarkeit natürlicher ganzer Zahlen als Summen von acht Quadraten und über ein mit diesem Problem zusammenhängendes nichtkommutatives und nichtassoziatives Zahlensystem“, Ber. Verh. Sächs. Akad. Wiss. Lipsko. Matematika. Fyz. Kl. , 76 : 63–82
Lahti, Usko (2015), Prof. Corvus Adamas: Luvut ja todistusmenetelmät. Johannto matematiikan perusteisiin innokkaiden opiskelijoiden seurassa. , Helsinky: Books on Demand, ISBN 978-952-318-558-6
Salzmann, Helmut; Betten, Dieter; Grundhöfer, Theo; Hähl, Hermann; Löwen, Rainer; Stroppel, Markus (1995), Kompaktní projektivní roviny, s úvodem do oktonové geometrie , De Gruyterovy expozice v matematice, Walter de Gruyter, ISBN 3-11-011480-1, ISSN 0938-6572 , OCLC 748698685
van der Blij, F. (1961), „Historie oktáv.“, Simon Stevin , 34 : 106–125, MR 0130283

externí odkazy

„Cayleyova čísla“ , Encyklopedie matematiky , EMS Press , 2001 [1994]
Wilson, RA (2008), Octonions (PDF) , poznámky k semináři Pure Mathematics

Languages

In other projects