Pentagon - Pentagon

Pentagon
Rovnostranný pětiúhelník, tj. Pětiúhelník, jehož pět stran má všechny stejnou délku
Hrany a vrcholy	5
Vnitřní úhel ( stupně )	108 ° (je -li rovnostranný, včetně pravidelného)

V geometrii je pětiúhelník (z řeckého πέντε pente znamená pět a γωνία gonia znamená úhel ) jakýkoli pětistranný mnohoúhelník nebo 5-gon. Součet vnitřních úhlů v jednoduchém pětiúhelníku je 540 °.

Pentagon může být jednoduchý nebo se sám protíná . Samo-protínající se pravidelný pětiúhelník (nebo hvězdný pětiúhelník ) se nazývá pentagram .

Pravidelné pětiúhelníky

Pravidelný pětiúhelník
Pravidelný pětiúhelník
Typ	Pravidelný mnohoúhelník
Hrany a vrcholy	5
Symbol Schläfli	{5}
Coxeterův diagram
Skupina symetrie	Vzepětí (D 5 ), pořadí 2 × 5
Vnitřní úhel ( stupně )	108 °
Duální mnohoúhelník	Já
Vlastnosti	Konvexní , cyklické , rovnostranné , izogonální , izotoxické

Strana ( ), poloměr kružnice ( ), poloměr vepsané kružnice ( ), výška ( ) , šířka/úhlopříčka ( )${\ displaystyle t}$${\ displaystyle R}$${\ displaystyle r}$${\ displaystyle R+r}$${\ Displaystyle \ varphi t}$

Pravidelný pětiúhelník má Schläfli symbol {5} a vnitřní úhly 108 °.

Pravidelný pětiúhelník má pět řádků reflectional symetrie a rotační symetrii řádu 5 (přes 72 °, 144 °, 216 ° a 288 °). Na diagonály příslušníky konvexní pravidelného pětiúhelníku jsou ve zlatém poměru k jeho stranách. Jeho výška (vzdálenost z jedné strany k opačnému vrcholu) a šířka (vzdálenost mezi dvěma nejvzdálenějšími oddělenými body, která se rovná délce diagonály) jsou dány vztahem

${\ displaystyle {\ text {Height}} = {\ frac {\ sqrt {5+2 {\ sqrt {5}}}} {2}} \ cdot {\ text {Side}} \ cca 1,539 \ cdot {\ text {Side}},}$

${\ displaystyle {\ text {Width}} = {\ text {Diagonal}} = {\ frac {1+{\ sqrt {5}}} {2}} \ cdot {\ text {Side}} \ cca 1,618 \ cdot {\ text {Side}},}$

${\ Displaystyle {\ text {Width}} = {\ sqrt {2-{\ frac {2} {\ sqrt {5}}}}} \ cdot {\ text {Height}} \ cca 1,051 \ cdot {\ text {Výška}},}$

${\ Displaystyle {\ text {Diagonal}} = R \ {\ sqrt {\ frac {5+{\ sqrt {5}}} {2}}} = 2R \ cos 18^{\ circ} = 2R \ cos { \ frac {\ pi} {10}} \ cca 1,902R,}$

kde R je poloměr kružnice .

Plocha konvexního pravidelného pětiúhelníku s délkou strany t je dána vztahem

${\ Displaystyle A = {\ frac {t^{2} {\ sqrt {25+10 {\ sqrt {5}}}}} {4}} = {\ frac {5t^{2} \ tan (54^ {\ circ})} {4}} = {\ frac {{\ sqrt {5 (5+2 {\ sqrt {5}})}} t^{2}} {4}} \ cca 1,720 t^{ 2}.}$

Pentagram nebo Pentangle je pravidelná hvězda pětiúhelník. Jeho symbol Schläfli je {5/2}. Jeho strany tvoří úhlopříčky pravidelného konvexního pětiúhelníku - v tomto uspořádání jsou strany obou pětiúhelníků ve zlatém řezu .

Když je pravidelný pětiúhelník ohraničen kružnicí o poloměru R , je délka jeho okraje t dána výrazem

${\ Displaystyle t = R \ {\ sqrt {\ frac {5-{\ sqrt {5}}} {2}}} = 2R \ sin 36^{\ circle} = 2R \ sin {\ frac {\ pi} {5}} \ cca 1,176R,}$

a jeho oblast je

${\ Displaystyle A = {\ frac {5R^{2}} {4}} {\ sqrt {\ frac {5+{\ sqrt {5}}} {2}}};}$

protože plocha ohraničené kružnice je pravidelný pětiúhelník, vyplňuje přibližně 0,7568 jeho ohraničené kružnice. ${\ displaystyle \ pi R^{2},}$

Odvození vzorce plochy

Oblast jakéhokoli pravidelného mnohoúhelníku je:

${\ displaystyle A = {\ frac {1} {2}} Pr}$

kde P je obvod polygonu a r je inradius (ekvivalentně apothem ). Náhradou hodnot pravidelného pětiúhelníku pro P a r vznikne vzorec

${\ Displaystyle A = {\ frac {1} {2}} \ cdot 5t \ cdot {\ frac {t \ tan ({\ frac {3 \ pi} {10}})} {2}} = {\ frac {5t^{2} \ tan ({\ frac {3 \ pi} {10}})} {4}}}$

s délkou strany t .

Inradius

Podobně jako každý pravidelný konvexní mnohoúhelník má pravidelný konvexní pětiúhelník vepsaný kruh . Apothem , což je poloměr r vepsané kružnice, pravidelného pětiúhelníku je spojena s boční délkou t o

${\ Displaystyle r = {\ frac {t} {2 \ tan (\ pi /5)}}} = {\ frac {t} {2 {\ sqrt {5-{\ sqrt {20}}}}}}} \ \ přibližně 0,6882 \ cdot t.}$

Akordy od ohraničené kružnice k vrcholům

Jako každý pravidelný konvexní mnohoúhelník má pravidelný konvexní pětiúhelník ohraničený kruh . Pro pravidelný pětiúhelník s postupnými vrcholy A, B, C, D, E, pokud P je jakýkoli bod na kružnici mezi body B a C, pak PA + PD = PB + PC + PE.

Bod v rovině

Pro libovolný bod v rovině pravidelného pětiúhelníku s circumradius , jehož vzdálenost k těžišti pravidelný pětiúhelník a jejích prvních pěti vrcholy jsou i v tomto pořadí, máme ${\ displaystyle R}$${\ displaystyle L}$${\ displaystyle d_ {i}}$

${\ Displaystyle \ textstyle \ sum _ {i = 1}^{5} d_ {i}^{2} = 5 (R^{2}+L^{2}),}$

${\ Displaystyle \ textstyle \ sum _ {i = 1}^{5} d_ {i}^{4} = 5 ((R^{2}+L^{2})^{2}+2R^{2 } L^{2}),}$

${\ Displaystyle \ textstyle \ sum _ {i = 1}^{5} d_ {i}^{6} = 5 ((R^{2}+L^{2})^{3}+6R^{2 } L^{2} (R^{2}+L^{2})),}$

${\ Displaystyle \ textstyle \ sum _ {i = 1}^{5} d_ {i}^{8} = 5 ((R^{2}+L^{2})^{4}+12R^{2 } L^{2} (R^{2}+L^{2})^{2}+6R^{4} L^{4}).}$

Pokud jsou vzdálenosti od vrcholů pravidelného pětiúhelníku k jakémukoli bodu na jeho kružnici, pak ${\ displaystyle d_ {i}}$

${\ Displaystyle 3 (\ textstyle \ sum _ {i = 1}^{5} d_ {i}^{2})^{2} = 10 \ textstyle \ sum _ {i = 1}^{5} d_ { i}^{4}.}$

Stavba pravidelného pětiúhelníku

Pravidelný pětiúhelník je konstruovatelný pomocí kompasu a pravítka , protože 5 je primární Fermat . Pro konstrukci pravidelného pětiúhelníku je známá řada metod. Některé jsou diskutovány níže.

Richmondova metoda

Jeden způsob konstrukce pravidelného pětiúhelníku v daném kruhu je popsán Richmondem a dále diskutován v Cromwellově Polyhedře .

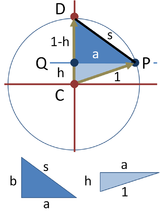
Horní panel ukazuje konstrukci použitou v Richmondově metodě k vytvoření strany vepsaného pětiúhelníku. Kruh definující pětiúhelník má jednotkový poloměr. Jeho střed se nachází v bodě C a střed M je označen v polovině jeho poloměru. Tento bod je připojen k obvodu vertikálně nad středem v bodě D . Úhel CMD je větvených a sečna protíná svislou osu v bodě Q . Vodorovná čára přes Q protíná kružnici v bodě P a akord PD je požadovanou stranou vepsaného pětiúhelníku.

K určení délky této strany jsou pod kruhem znázorněny dva pravé trojúhelníky DCM a QCM . Pomocí Pythagorovy věty a dvou stran je přepona většího trojúhelníku nalezena jako . Strana h menšího trojúhelníku se pak najde pomocí vzorce polovičního úhlu : ${\ displaystyle \ scriptstyle {\ sqrt {5}}/2}$

${\ Displaystyle \ tan (\ phi /2) = {\ frac {1- \ cos (\ phi)} {\ sin (\ phi)}} \,}$

kde kosinus a sinus ϕ jsou známy z většího trojúhelníku. Výsledek je:

${\ displaystyle h = {\ frac {{\ sqrt {5}}-1} {4}} \.}$

S touto známou stranou se pozornost obrátí ke spodnímu diagramu, aby našla strany s pravidelného pětiúhelníku. Za prvé, strana a pravoúhlého trojúhelníku je opět nalezena pomocí Pythagorovy věty:

${\ Displaystyle a^{2} = 1-h^{2} \; \ a = {\ frac {1} {2}} {\ sqrt {\ frac {5+{\ sqrt {5}}} {2 }}} \.}$

Potom se s najde pomocí Pythagorovy věty a levostranného trojúhelníku jako:

${\ Displaystyle s^{2} = (1-h)^{2}+a^{2} = (1-h)^{2}+1-h^{2} = 1-2h+h^{ 2}+1-h^{2} = 2-2h = 2-2 \ vlevo ({\ frac {{\ sqrt {5}}-1} {4}} \ vpravo) \}$

${\ displaystyle = {\ frac {5-{\ sqrt {5}}} {2}} \.}$

Strana s je tedy:

${\ Displaystyle s = {\ sqrt {\ frac {5-{\ sqrt {5}}} {2}}} \,}$

což je dobře zavedený výsledek.

Kruhy Carlyle

Metoda pomocí kruhů Carlyle

Carlyleův kruh byl vynalezen jako geometrická metoda k nalezení kořenů kvadratické rovnice . Tato metodika vede k postupu pro konstrukci pravidelného pětiúhelníku. Kroky jsou následující:

1. Nakreslit kruh , ve kterém k zapisování pětiúhelník a označit středového bodu O .
2. Středem kruhu nakreslete vodorovnou čáru. Označit levý křižovatku s kruhu jako bod B .
3. Vytvořte svislou čáru uprostřed. Označit jednu křižovatku s kruhu jako bod A .
4. Construct bod M jako středu O a B .
5. Nakreslit kružnici se středem na M prostřednictvím bodu A . Označte jeho průsečíku s vodorovnou linií (uvnitř původního kruhu) jako bod W a její průsečík vně kruhu jako bodu V .
6. Nakreslit kružnici o poloměru OA a středové W . Protíná původní kruh na dvou vrcholech pětiúhelníku.
7. Nakreslit kružnici o poloměru OA a středové V . Protíná původní kruh na dvou vrcholech pětiúhelníku.
8. Pátý vrchol je pravý průsečík vodorovné čáry s původní kružnicí.

Kroky 6–8 jsou ekvivalentní následující verzi zobrazené v animaci:

6a. Sestrojte bod F jako střed O a W.

7a. Vytvořte svislou čáru skrz F. Protíná původní kružnici na dvou vrcholech pětiúhelníku. Třetí vrchol je pravý průsečík vodorovné čáry s původní kružnicí.

8a. Sestrojte další dva vrcholy pomocí kompasu a délky vrcholu nalezeného v kroku 7a.

Pomocí trigonometrie a Pythagorovy věty

Pomocí trigonometrie a Pythagorovy věty sestrojte pravidelný pětiúhelník.

Konstrukce

1. Nejprve si všimneme, že pravidelný pětiúhelník lze rozdělit na 10 shodných trojúhelníků, jak ukazuje pozorování . Také cos 36 ° = . † †${\ displaystyle {\ tfrac {1+{\ sqrt {5}}} {4}}}$
2. V kroku 1 použijeme čtyři jednotky (zobrazené modře) a pravý úhel k sestavení segmentu o délce 1+ √ 5 , konkrétně vytvořením 1-2- √ 5 pravoúhlého trojúhelníku a poté prodloužením přepony √ 5 o a délka 1. Poté tento segment rozdělíme na polovinu - a poté znovu na dvě poloviny - vytvoříme segment délky (zobrazený červeně).${\ displaystyle {\ tfrac {1+{\ sqrt {5}}} {4}}}$
3. V kroku 2 sestrojíme dva soustředné kruhy se středem na O s poloměry délky 1 a délky . Poté umístíme P libovolně na menší kruh, jak je znázorněno. Sestrojením přímky kolmé na OP procházející P sestrojíme první stranu pětiúhelníku pomocí bodů vytvořených v průsečíku tečny a jednotkové kružnice. Čtyřnásobné zkopírování této délky podél vnějšího okraje kruhů jednotek nám dává pravidelný pětiúhelník.${\ displaystyle {\ tfrac {1+{\ sqrt {5}}} {4}}}$

† Důkaz, že cos 36 ° = ${\ displaystyle {\ tfrac {1+{\ sqrt {5}}} {4}}}$

${\ displaystyle 0 = \ cos 90^{\ circ}}$

${\ displaystyle = \ cos (72^{\ circ} +18^{\ circ})}$

${\ Displaystyle = \ cos 72^{\ circ} \ cos 18^{\ circ}-\ sin 72^{\ circle} \ sin 18^{\ circle}}$(pomocí vzorce pro přidání úhlu pro kosinus )

${\ Displaystyle = (2 \ cos^{2} 36^{\ circ} -1) {\ sqrt {\ tfrac {1+ \ cos 36^{\ circle}} {2}}}-2 \ sin 36^ {\ circ} \ cos 36^{\ circle} {\ sqrt {\ tfrac {1- \ cos 36^{\ circle}} {2}}}}$(pomocí vzorců s dvojitým a polovičním úhlem )

Nechť u = cos 36 °. Nejprve si všimněte, že 0 < u <1 (což nám pomůže při práci zjednodušit). Nyní,

${\ displaystyle {\ begin {aligned} 0 & {} = (2u^{2} -1) {\ sqrt {\ tfrac {1+u} {2}}}-2 {\ sqrt {1-u^{2 }}} \ cdot u {\ sqrt {\ tfrac {1-u} {2}}} \\ 2 {\ sqrt {1-u^{2}}} \ cdot u {\ sqrt {\ tfrac {1- u} {2}}} & {} = (2u^{2} -1) {\ sqrt {\ tfrac {1+u} {2}}} \\ 2 {\ sqrt {1+u}} {\ sqrt {1-u}} \ cdot u {\ sqrt {1-u}} & {} = (2u^{2} -1) {\ sqrt {1+u}} \\ 2u (1-u) & {} = 2u^{2} -1 \\ 2u-2u^{2} & {} = 2u^{2} -1 \\ 0 & {} = 4u^{2} -2u-1 \\ u & {} = {\ frac {2+{\ sqrt {(-2)^{2} -4 (4) (-1)}}}} {2 (4)}} \ \ u & {} = {\ frac {1+ {\ sqrt {5}}} {4}} \ end {aligned}}}$

Rychle to vyplývá z poznání, že dvakrát sinus 18 stupňů je reciproční zlatý řez, který známe geometricky z trojúhelníku s úhly 72,72,36 stupně. Z trigonometrie víme, že kosinus dvakrát 18 stupňů je 1 minus dvojnásobek čtverce sinusu 18 stupňů, a to se redukuje na požadovaný výsledek jednoduchou kvadratickou aritmetikou.

Délka strany je dána

Pravidelné pětiúhelník podle zlatého řezu , dělení úsečku od vnější dělení

Pentagon při dané délce strany

1. Nakreslete segment AB, jehož délka je daná strana pětiúhelníku.
2. Prodlužte segment BA z bodu A asi o tři čtvrtiny segmentu BA .
3. Nakreslete oblouk kružnice, středový bod B , s poloměrem AB .
4. Nakreslete oblouk kružnice, středový bod A , s poloměrem AB ; vyvstává průsečík F .
5. Sestrojte kolmici na segment AB bodem F ; vyvstává průsečík G .
6. Nakreslete přímku rovnoběžnou se segmentem FG z bodu A do kruhového oblouku kolem bodu A ; vzniká průsečík H .
7. Nakreslete oblouk kružnice, středový bod G s poloměrem GH k prodloužení segmentu AB ; vzniká průsečík J .
8. Nakreslete oblouk kruhu, středový bod B s poloměrem BJ ke kolmici v bodě G ; vzniká průsečík D na kolmici, a průsečík E s kruhovým obloukem, který byl vytvořen kolem bodu A .
9. Nakreslete oblouk kruhu, středový bod D , s poloměrem BA, dokud tento kruhový oblouk nepřekročí druhý kruhový oblouk kolem bodu B ; vyvstává průsečík C .
10. Spojte body BCDEA . Výsledkem je pětiúhelník.

Zlatý řez

${\ displaystyle {\ frac {\ overline {BJ}} {\ overline {AB}}} = {\ frac {\ overline {AB}} {\ overline {AJ}}} = {\ frac {1+{\ sqrt {5}}} {2}} = \ varphi \ přibližně 1,618}$

Euklidova metoda

Euclidova metoda pro pětiúhelník v daném kruhu, použití zlatého trojúhelníku , animace 1 min 39 s

Pravidelný pětiúhelník je konstruovatelný pomocí kompasu a pravítka, a to buď zapsáním jednoho do daného kruhu, nebo vytvořením jednoho na daném okraji. Tento proces popsal Euclid ve svých Prvcích kolem roku 300 př. N. L.

Jednoduše pomocí úhloměru (nejedná se o klasickou konstrukci)

Následuje přímá metoda pomocí stupňů:

1. Nakreslete kruh a vyberte bod, který bude pětiúhelníkem (např. Uprostřed uprostřed)
2. Vyberte bod A v kruhu, který bude sloužit jako jeden vrchol pětiúhelníku. Nakreslit čáru přes O a A .
3. Nakreslete přes něj a střed kruhu vodicí čáru
4. Nakreslete čáry v úhlu 54 ° (od vodicí čáry) protínající bod pětiúhelníku
5. Tam, kde protínají kruh, nakreslete čáry pod úhlem 18 ° (od rovnoběžek k vodítku)
6. Připojte se tam, kde protínají kruh

Po vytvoření pravidelného konvexního pětiúhelníku, pokud se někdo spojí s nesousedícími rohy (nakreslí úhlopříčky pětiúhelníku), získá pentagram s menším pravidelným pětiúhelníkem uprostřed. Nebo pokud někdo prodlouží strany, dokud se nesousedící strany nesetkají, získá větší pentagram. Přesnost této metody závisí na přesnosti úhloměru použitého k měření úhlů.

Fyzikální metody

Overhand uzel pásu papíru

• Pravidelný pětiúhelník může být vytvořen z pouhého pruhu papíru tím, že do pásu uvázáte vrchní uzel a uzel opatrně zploštíte zatažením za konce papírového pásu. Přeložením jednoho z konců zpět na pětiúhelník odhalíte při podsvícení pentagram .
• Postavte pravidelný šestiúhelník na tvrdý papír nebo kartu. Mačkejte podél tří průměrů mezi protilehlými vrcholy. Vystřihněte z jednoho vrcholu do středu, aby vznikla rovnostranná trojúhelníková klapka. Opravte tuto klapku pod sousedem a vytvořte pětiúhelníkovou pyramidu . Základna pyramidy je pravidelný pětiúhelník.

Symetrie

Symetrie pravidelného pětiúhelníku. Vrcholy jsou vybarveny podle jejich poloh symetrie. Modré zrcadlové čáry se kreslí vrcholy a hranami. Ve středu se vydávají příkazy k pohybu.

Pravidelný pětiúhelník má Dih ₅ symetrii , objednat 10. Vzhledem k tomu, 5 je prvočíslo je jedna podskupina se prostorový úhel symetrie: Dih ₁ a 2 cyklická skupina symetrie: Z ₅ a Z ₁ .

Tyto 4 symetrie lze vidět ve 4 odlišných symetriích na pětiúhelníku. John Conway je označí dopisem a skupinovou objednávkou. Plná symetrie pravidelného tvaru je r10 a žádná symetrie není označena a1 . Symetrie vzepětí jsou rozděleny podle toho, zda procházejí vrcholy ( d pro diagonály) nebo hranami ( p pro kolmice), a i když čáry odrazu procházejí hranami i vrcholy. Cyklické symetrie ve středním sloupci jsou označeny jako g pro jejich centrální gyrační řády.

Každá symetrie podskupiny umožňuje jeden nebo více stupňů volnosti pro nepravidelné tvary. Pouze podskupina g5 nemá žádné stupně volnosti, ale lze ji vidět jako směrované hrany .

Rovnostranné pětiúhelníky

Rovnostranný pětiúhelník postavený se čtyřmi stejnými kruhy uspořádanými v řetězu.

Rovnostranný pětiúhelník je mnohoúhelník s pěti stejně dlouhými stranami. Jeho pět vnitřních úhlů však může mít řadu sad hodnot, což mu umožňuje vytvořit rodinu pětiúhelníků. Naproti tomu pravidelný pětiúhelník je jedinečný až do podobnosti, protože je rovnostranný a je rovnostranný (jeho pět úhlů je shodných).

Cyklické pětiúhelníky

Cyklický pětiúhelník je jeden pro který kruh nazývá circumcircle prochází všemi pěti vrcholy. Pravidelný pětiúhelník je příkladem cyklického pětiúhelníku. Plochu cyklického pětiúhelníku, ať už pravidelného nebo ne, lze vyjádřit jako jednu čtvrtinu druhé odmocniny jednoho z kořenů septické rovnice, jejíž koeficienty jsou funkcemi stran pětiúhelníku.

Existují cyklické pětiúhelníky s racionálními stránkami a racionální oblastí; těm se říká Robbinsovy pětiúhelníky . Bylo prokázáno, že úhlopříčky Robbinsova pětiúhelníku musí být buď všechny racionální, nebo všechny iracionální, a předpokládá se, že všechny úhlopříčky musí být racionální.

Obecné konvexní pětiúhelníky

U všech konvexních pětiúhelníků je součet čtverců úhlopříček menší než 3násobek součtu čtverců stran.

Grafy

Kompletní graf K ₅ je často kreslen jako pravidelný pětiúhelník se všemi 10 hranami spojenými. Tento graf také představuje ortografickou projekci 5 vrcholů a 10 okrajů 5 buněk . Opraveny 5-buněk , s vrcholy v polovině hrany 5-buněk se očekává uvnitř pětiúhelníku.

5článkový (4D)

Usměrněné 5článkové (4D)

Příklady pětiúhelníků

Rostliny

• 

  Pentagonální průřez okra .

• 

  Ranní sláva , stejně jako mnoho jiných květin, má pětiúhelníkový tvar.

• 

  Gyneceum z jablka obsahuje pět carpels, uspořádané v pěticípé hvězdy

• 

  Starfruit je další ovoce s pětinásobnou symetrií.

Zvířata

• 

  Sea star . Mnoho ostnokožců má pětinásobnou radiální symetrii.

• 

  Další příklad echinodermu, endoskeletu mořského ježka .

• 

  Ilustrace křehkých hvězd , také ostnokožců s pětiúhelníkovým tvarem.

Minerály

• 

  Iosahedrální kvazikrystal Ho-Mg-Zn vytvořený jako pětiúhelníkový dvanáctistěn . Tváře jsou pravými pravidelnými pětiúhelníky.

• 

  Pyritohedral krystal pyritu . Pyritohedron má 12 identických pětiúhelníkových ploch, které nejsou omezeny jako pravidelné.

Umělý

• 

  Pentagon , ředitelství amerického ministerstva obrany .

• 

  Home desku na baseballové hřiště

Pentagony v obkladech

Nejznámější balení ze stejně velkých pravidelných pětiúhelníků v rovině, je dvojitá mřížka struktura, která se vztahuje na 92.131% roviny.

Pravidelný pětiúhelník se nemůže objevit v žádném obkladu pravidelných mnohoúhelníků. Za prvé, abychom dokázali, že pětiúhelník nemůže tvořit pravidelný obklad (takový, ve kterém jsou všechny plochy shodné, což vyžaduje, aby všechny polygony byly pětiúhelníky), pozorujte, že 360 ° / 108 ° = 3 1 ⁄ 3 (kde 108 ° je vnitřní úhel ), což není celé číslo; proto neexistuje žádný celočíselný počet pětiúhelníků sdílejících jeden vrchol a nezůstávající mezi nimi mezery. Obtížnější je dokázat, že pětiúhelník nemůže být v žádném obkladu od okraje k okraji vytvořeném pravidelnými polygony:

Maximální známá hustota balení pravidelného pětiúhelníku je přibližně 0,921, čehož je dosaženo zobrazením dvojité mřížky . V předtisku vydaném v roce 2016 oznámili Thomas Hales a Wöden Kusner důkaz, že dvojité mřížkové balení pravidelného pětiúhelníku (kterému říkají balení „pětiúhelníkového ledového paprsku“ a které vysledují na práci čínských řemeslníků v roce 1900) má optimální hustotu mezi všemi baleními pravidelných pětiúhelníků v rovině. Od roku 2020 jejich důkaz nebyl dosud posouzen a zveřejněn.

Neexistují žádné kombinace pravidelných mnohoúhelníků se 4 nebo více setkáními na vrcholu, které obsahují pětiúhelník. U kombinací se 3 platí, že pokud se 3 mnohoúhelníky setkají na vrcholu a jeden má lichý počet stran, musí být druhé 2 shodné. Důvodem je to, že mnohoúhelníky, které se dotýkají okrajů pětiúhelníku, se musí střídat kolem pětiúhelníku, což je nemožné kvůli lichému počtu stran pětiúhelníku. Pro pětiúhelník to má za následek mnohoúhelník, jehož všechny úhly jsou (360 - 108) / 2 = 126 ° . Abychom zjistili počet stran, které tento polygon má, je výsledkem 360 / (180 - 126) = 6 2 ⁄ 3 , což není celé číslo. Pentagon se proto nemůže objevit v žádném obkladu vytvořeném pravidelnými mnohoúhelníky.

Existuje 15 tříd pětiúhelníků, které mohou monohedrálně dlaždit letadlo . Žádný z pětiúhelníků nemá obecně žádnou symetrii, i když některé mají speciální případy se zrcadlovou symetrií.

15 monohedrálních pětibokých dlaždic

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15

Pentagony v mnohostěnu

Já h	T h	T d	Ó	Já	D 5d
Dodecahedron	Pyritohedron	Tetartoid	Pentagonální icositetrahedron	Pětiúhelníkový šestihran	Zkrácený lichoběžník

Viz také

• Associahedron ; Pentagon je čtyřúhelník řádu 4
• Dodecahedron , mnohostěn, jehož pravidelná forma se skládá z 12 pětibokých ploch
• Zlatý řez
• Seznam geometrických tvarů
• Pentagonální čísla
• Pentagram
• Pentagramová mapa
• Pentastar , logo Chrysler
• Pythagorova věta#Podobné obrázky na třech stranách
• Trigonometrické konstanty pro pětiúhelník

Řádkové poznámky a odkazy

externí odkazy

• Weisstein, Eric W. „Pentagon“ . MathWorld .
• Animovaná ukázka konstrukce vepsaného pětiúhelníku s kompasem a pravítkem.
• Jak postavit pravidelný pětiúhelník pouze s kompasem a pravítkem.
• Jak složit pravidelný pětiúhelník pouze pomocí pásu papíru
• Definice a vlastnosti pětiúhelníku s interaktivní animací
• Přibližné stavby renesančních umělců pravidelných pětiúhelníků
• Pentagon. Jak vypočítat různé rozměry pravidelných pětiúhelníků.