Fázový prostor - Phase space

Diferenciální rovnice
Navier – Stokesovy diferenciální rovnice používané k simulaci proudění vzduchu kolem překážky
Rozsah Přírodní vědy Inženýrství Astronomie Fyzika Chemie Biologie Geologie Aplikovaná matematika Mechanika kontinua Teorie chaosu Dynamické systémy Společenské vědy Ekonomika Populační dynamika
Klasifikace
Typy Obyčejný Částečný Diferenciálně algebraické Integro-diferenciál Frakční Lineární Nelineární Podle typu proměnné Závislé a nezávislé proměnné Autonomní Komplex Spojeno / Odpojeno Přesný Homogenní  / nehomogenní Funkce Objednat Operátor Zápis
Vztah k procesům Rozdíl (diskrétní analogový) Stochastický Stochastické částečné Zpoždění
Řešení
Existence a jedinečnost Picard – Lindelöfova věta Věta o Peanově existenci Carathéodoryho věta o existenci Cauchy – Kowalevského věta
Obecná témata Wronskian Fázový portrét Fázový prostor Lyapunov  / asymptotická  / exponenciální stabilita Míra konvergence Sériová  / integrální řešení Numerická integrace Diracova delta funkce
Metody řešení Inspekce Metoda charakteristik Euler Vzorec exponenciální odezvy Konečný rozdíl  ( Crank – Nicolson ) Konečný element Nekonečný prvek Konečný objem Galerkin Petrov – Galerkin Integrační faktor Integrální transformace Poruchová teorie Runge – Kutta Oddělení proměnných Neurčené koeficienty Variace parametrů
Lidé Isaac Newton Gottfried Leibniz Leonhard Euler Émile Picard Józef Maria Hoene-Wroński Ernst Lindelöf Rudolf Lipschitz Augustin-Louis Cauchy John Crank Phyllis Nicolson Carl David Tolmé Runge Martin Kutta
proti t E

Fázová cesta oscilátoru Duffing

Fázový prostor dynamického systému s ohniskovou stabilitou, ukazující trajektorii jednofázového prostoru

V teorie dynamického systému , je fázový prostor je prostor , ve kterém všechny možné stavy v systému jsou znázorněny, přičemž každá možné stav odpovídá zařazeny do jednoho bodu ve fázovém prostoru. U mechanických systémů se fázový prostor obvykle skládá ze všech možných hodnot proměnných polohy a hybnosti . Je to vnější produkt přímého prostoru a vzájemného prostoru . Koncept fázového prostoru vyvinuli na konci 19. století Ludwig Boltzmann , Henri Poincaré a Josiah Willard Gibbs .

Úvod

Ve fázovém prostoru je každý stupeň volnosti nebo parametr systému reprezentován jako osa vícerozměrného prostoru; jednorozměrný systém se nazývá fázová čára , zatímco dvourozměrný systém se nazývá fázová rovina . Pro každý možný stav systému nebo povolenou kombinaci hodnot parametrů systému je do vícerozměrného prostoru zahrnut bod. Vyvíjející se stav systému v průběhu času sleduje cestu ( trajektorii fázového prostoru pro systém) skrz prostor vysokého prostoru. Trajektorie fázového prostoru představuje množinu stavů kompatibilních s počátkem od jedné konkrétní počáteční podmínky , která se nachází v úplném fázovém prostoru, který představuje množinu stavů kompatibilních s počátkem od jakékoli počáteční podmínky. Fázový diagram jako celek představuje vše, čím systém může být, a jeho tvar může snadno objasnit vlastnosti systému, které by jinak nebyly zřejmé. Fázový prostor může obsahovat velké množství rozměrů. Například, plyn obsahující mnoho molekul může vyžadovat samostatný rozměr každé částice v x , y a z, pozic a hybností (6 rozměry pro idealizované monatomic plyn), a pro složitější molekulárních systémů další rozměry nutné popsat vibračních režimů molekulární vazby a také se točí kolem 3 os. Fázové prostory se snáze používají při analýze chování mechanických systémů omezených na pohyb kolem a podél různých os rotace nebo translace - např. V robotice, jako je analýza rozsahu pohybu robotického ramene nebo stanovení optimální cesty k dosažení konkrétní polohy / výsledek hybnosti.

Vývoj souboru klasických systémů ve fázovém prostoru (nahoře). Systémy jsou masivní částice v jednorozměrné potenciálové jámě (červená křivka, spodní obrázek). Zpočátku kompaktní celek se postupem času rozvířil.

Konjugujte momentu

V klasické mechanice, na výběr z zobecněné souřadnice q _i na pozici (tj poloha na prostoru konfigurace ) definuje konjugát zobecněné momenta p _i , které společně definují souřadnice na fázovém prostoru. Více abstraktně, v klasické mechanice je fázový prostor kotangensovým svazkem konfiguračního prostoru a v této interpretaci výše uvedený postup vyjadřuje, že volba lokálních souřadnic v konfiguračním prostoru vyvolá volbu přirozených místních Darbouxových souřadnic pro standardní symplektickou strukturu v kotangentním prostoru .

Statistické soubory ve fázovém prostoru

Pohyb souboru systémů v tomto prostoru je studován klasickou statistickou mechanikou . Místní hustota bodů v takových systémech se řídí Liouvilleovou větou , a lze ji tedy brát jako konstantní. V kontextu modelového systému v klasické mechanice jsou fázové prostorové souřadnice systému v daném okamžiku složeny ze všech dynamických proměnných systému. Z tohoto důvodu je možné vypočítat stav systému v kterémkoli daném čase v budoucnosti nebo v minulosti integrací Hamiltonových nebo Lagrangeových pohybových rovnic.

Příklady

Ilustrace toho, jak by byl zkonstruován fázový portrét pro pohyb jednoduchého kyvadla .

Tok časových řad ve fázovém prostoru specifikovaný diferenciální rovnicí kyvadla . Osa X odpovídá poloze kyvadla a osa Y jeho rychlost.

Nízké rozměry

U jednoduchých systémů může existovat jen jeden nebo dva stupně volnosti. Jeden stupeň volnosti nastává, když má člověk autonomní obyčejnou diferenciální rovnici v jedné proměnné, přičemž výsledný jednorozměrný systém se nazývá fázová čára a kvalitativní chování systému je okamžitě viditelné z fázové čáry. Nejjednoduššími netriviálními příklady jsou model / rozpad exponenciálního růstu (jedna nestabilní / stabilní rovnováha) a model logistického růstu (dvě rovnováhy, jedna stabilní a jedna nestabilní). ${\ displaystyle dy / dt = f (y),}$

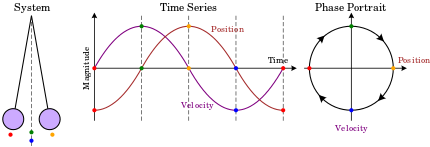
Fázový prostor dvourozměrného systému se nazývá fázová rovina , která se v klasické mechanice vyskytuje u jedné částice pohybující se v jedné dimenzi a kde dvěma proměnnými jsou poloha a rychlost. V tomto případě je náčrt fáze portrétu může poskytnout kvalitativní informace o dynamice systému, jako je například mezní cyklus v Van der Pol oscilátoru je znázorněno na obrázku.

Zde vodorovná osa udává rychlost polohy a svislá osa. Jak se systém vyvíjí, jeho stav sleduje jednu z linií (trajektorií) ve fázovém diagramu.

Fázový portrét na Van der Pol oscilátoru

Teorie chaosu

Klasické příklady fázových diagramů z teorie chaosu jsou:

• Lorenz atraktor
• populační růst (tj. logistická mapa )
• parametrická rovina komplexních kvadratických polynomů se sadou Mandelbrot .

Fázový graf

Graf proměnných polohy a hybnosti jako funkce času se někdy nazývá fázový diagram nebo fázový diagram . Druhý výraz, „ fázový diagram “, je však ve fyzikálních vědách obvykle vyhrazen pro diagram ukazující různé oblasti stability termodynamických fází chemického systému, který se skládá z tlaku , teploty a složení.

Kvantová mechanika

V kvantové mechanice se souřadnice p a q fázového prostoru normálně stávají Hermitovými operátory v Hilbertově prostoru .

Mohou si ale alternativně zachovat svou klasickou interpretaci, pokud budou jejich funkce skládat novými algebraickými způsoby (prostřednictvím Groenewoldova hvězdného produktu z roku 1946 ). To je v souladu s principem neurčitosti kvantové mechaniky. Každá kvantově mechanická pozorovatelnost odpovídá jedinečné funkci nebo distribuci ve fázovém prostoru a naopak, jak specifikoval Hermann Weyl (1927) a doplnil John von Neumann (1931); Eugene Wigner (1932); a ve velké syntéze HJ Groenewold (1946). S JE Moyalem (1949) dokončili základy formulace fázového prostoru kvantové mechaniky , kompletní a logicky autonomní přeformulování kvantové mechaniky. (Mezi jeho moderní abstrakce patří deformace a kvantizace geometrie .)

Očekávané hodnoty v kvantování fázového prostoru jsou získány izomorfně s trasováním pozorovatelných operátorů s maticí hustoty v Hilbertově prostoru: jsou získány integrály pozorovatelných fázových prostorů, přičemž jako měřítko účinně slouží Wignerova kvazi-pravděpodobnostní distribuce .

Tím, že expresí kvantové mechaniky ve fázovém prostoru (stejného rámce, jako pro klasické mechanice), je mapa Weyl usnadňuje rozpoznání kvantové mechaniky jako deformace (generalizace) klasické mechaniky, se deformace parametr ħ / S , kde S je akce z příslušný proces. (Další známé deformace ve fyzice zahrnují deformaci klasické newtonovské relativistické mechaniky s deformačním parametrem v / c ; nebo deformaci newtonovské gravitace do obecné relativity s deformačním parametrem Schwarzschildův poloměr / charakteristická dimenze.)

Klasické výrazy, pozorovatelnosti a operace (jako jsou Poissonovy závorky) jsou modifikovány ħ závislými kvantovými korekcemi, protože konvenční komutativní násobení aplikované v klasické mechanice je zobecněno na nekomutativní hvězdné násobení charakterizující kvantovou mechaniku a na jejím principu neurčitosti.

Termodynamika a statistická mechanika

V kontextech termodynamiky a statistické mechaniky má termín fázový prostor dva významy: pro jeden se používá ve stejném smyslu jako v klasické mechanice. Pokud se termodynamický systém skládá z N částic, pak bod v 6 N -rozměrném fázovém prostoru popisuje dynamický stav každé částice v tomto systému, protože každá částice je spojena s proměnnými tří pozic a třemi proměnnými hybnosti. V tomto smyslu, pokud jsou částice rozlišitelné , se říká, že bod ve fázovém prostoru je mikrostavem systému. (Pro nerozeznatelné částice bude mikrostav sestávat ze sady N ! Bodů, odpovídajících všem možným výměnám N částic.) N je obvykle v řádu Avogadrova čísla , takže popis systému na mikroskopické úrovni je často nepraktický. To vede k využití fázového prostoru v jiném smyslu.

Fázový prostor může také odkazovat na prostor, který je parametrizován makroskopickými stavy systému, jako je tlak, teplota atd. Například je možné zobrazit diagram tlaku a objemu nebo diagramy entropie a teploty jako popisující část této fáze prostor. Bod v tomto fázovém prostoru se příslušně nazývá makrostát. Se stejným makrostátem může snadno existovat více než jeden mikrostav. Například pro pevnou teplotu může mít systém mnoho dynamických konfigurací na mikroskopické úrovni. Pokud se použije v tomto smyslu, fáze je oblast fázového prostoru, kde se dotyčný systém nachází například v kapalné fázi nebo pevné fázi atd.

Jelikož existuje mnohem více mikrostavů než makrostátů, je fázový prostor v prvním smyslu obvykle varietou mnohem větších rozměrů než v druhém smyslu. Je zřejmé, že je zapotřebí mnohem více parametrů k registraci každého detailu systému až do molekulárního nebo atomového měřítka, než jednoduše specifikovat, řekněme, teplotu nebo tlak systému.

Optika

Fázový prostor je široce používán v nonimaging optice , odvětví optiky věnované osvětlení. Je to také důležitý koncept v hamiltonovské optice .

Fázový integrál

V klasické statistické mechanice (spojité energie) poskytuje koncept fázového prostoru klasický analog k rozdělovací funkci (součet přes stavy) známý jako fázový integrál. Místo součtu Boltzmannova faktoru nad diskrétně rozmístěnými energetickými stavy (definovanými příslušnými celočíselnými kvantovými čísly pro každý stupeň volnosti) lze integrovat přes spojitý fázový prostor. Taková integrace se v zásadě skládá ze dvou částí: integrace hybné složky všech stupňů volnosti (hybný prostor) a integrace polohové složky všech stupňů volnosti (konfigurační prostor). Jakmile je fázový integrál známý, může to souviset s klasickou rozdělovací funkcí vynásobením normalizační konstanty představující počet stavů kvantové energie na jednotku fázového prostoru. Tato normalizační konstanta je jednoduše inverzní k Planckově konstantě zvednuté na sílu rovnou počtu stupňů volnosti systému.

Viz také

Reference

Další čtení

• Nolte, DD (2015). Úvod do moderní dynamiky: chaos, sítě, prostor a čas . Oxford University Press. ISBN 978-0-19-965703-2.
• Nolte, DD (2018). Galileo Unbound: Cesta napříč životem, vesmírem a vším . Oxford University Press. ISBN 978-0-19-880584-7.

externí odkazy

• „Fázový prostor“ , Encyclopedia of Mathematics , EMS Press , 2001 [1994]