Schröder – Bernsteinova věta - Schröder–Bernstein theorem

V teorii množin se Schröder-Bernstein věta uvádí, že v případě, že existují injektivních funkce f  : A → B a g  : B → A mezi sadami A a B , pak existuje bijective funkce h  : A → B .

Z hlediska mohutnosti těchto dvou sad to klasicky znamená, že pokud | A | ≤ | B | a | B | ≤ | A | , pak | A | = | B | ; to znamená, že A a B jsou ekvipotentní . Toto je užitečná funkce při řazení základních čísel .

Věta je pojmenována po Felixovi Bernsteinovi a Ernstu Schröderovi . Je také známá jako Cantor – Bernsteinova věta nebo Cantor – Schröder – Bernstein podle Georga Cantora, který ji poprvé publikoval bez důkazu.

Důkaz

Definice Konig je z bijection h :  →  B z daných například injekcí f : A  →  B a g : B  →  A . Prvek v A a B je označen číslem a písmenem. Sekvence 3 → e → 6 → ... je stopka A , vedoucí k definicím h (3) =  f (3) =  e , h (6) =  f (6), .... Pořadí d  → 5 →  f  → ... je B -doraz, vedoucí k h (5) =  g ⁻¹ (5) =  d , .... Pořadí ... →  a  → 1 →  c  → 4 → .. . je dvojnásobně nekonečný, což vede k h (1) =  g ⁻¹ (1) =  a , h (4) =  g ⁻¹ (4) =  c , .... Posloupnost b  → 2 →  b je cyklická, vedoucí do h (2) =  g ⁻¹ (2) =  b .

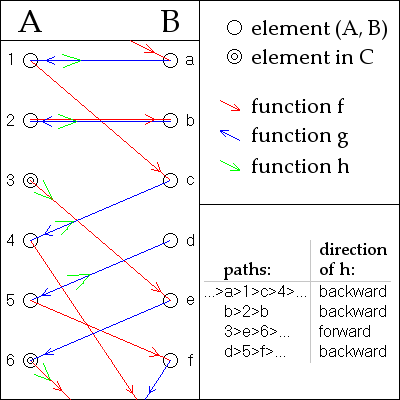
Následující důkaz je přičítán Juliusovi Königovi .

Předpokládejme beze ztráty obecnosti, že A a B jsou nesouvislé . Pro libovolné a v A nebo b v B můžeme vytvořit jedinečnou oboustrannou posloupnost prvků, které jsou střídavě v A a B , opakovaným použitím a přechodem z A do B a a přechodem z B do A (kde je definováno; inverzní a jsou v této fázi důkazu chápány jako dílčí funkce .) ${\ displaystyle f}$${\ displaystyle g^{-1}}$${\ displaystyle g}$${\ displaystyle f^{-1}}$${\ displaystyle f^{-1}}$${\ displaystyle g^{-1}}$

${\ Displaystyle \ cdots \ rightarrow f^{-1} (g^{-1} (a)) \ rightarrow g^{-1} (a) \ rightarrow a \ rightarrow f (a) \ rightarrow g (f ( a)) \ rightarrow \ cdots}$

U jakéhokoli konkrétního a může tato sekvence končit doleva nebo ne, v místě, kde nebo není definováno. ${\ displaystyle f^{-1}}$${\ displaystyle g^{-1}}$

Tím, že a jsou injektivní funkce, každá a v A a b v B je přesně v jedné takové posloupnosti v rámci identity: pokud se prvek vyskytuje ve dvou posloupnostech, všechny prvky nalevo a napravo musí být stejné v obou definicí sekvencí. Proto sekvence tvoří oddíl o (disjoint) spojení A a B . Proto stačí vytvořit bijekci mezi prvky A a B v každé ze sekvencí samostatně, a to následovně: ${\ displaystyle f}$${\ displaystyle g}$

Volání sekvenci s A-zátky , pokud se zastaví u prvku A , nebo B-zátkou , pokud se zastaví u prvku B . Jinak to nazývejte dvojnásobně nekonečné, pokud jsou všechny prvky odlišné nebo cyklické, pokud se to opakuje. Příklady viz obrázek.

• Pro A-zátkou , funkce je bijection mezi jeho prvky A a jejích prvků B .${\ displaystyle f}$
• U B-zátky , funkce je bijection mezi jeho prvky B a jeho prvků v A .${\ displaystyle g}$
• Pro dvojnásobně nekonečnou sekvenci nebo cyklickou sekvenci bude stačit buď nebo bude ( je použito na obrázku).${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle g}$

Dějiny

Tradiční název „Schröder – Bernstein“ je založen na dvou důkazech publikovaných nezávisle v roce 1898. Cantor je často přidáván, protože poprvé uvedl větu v roce 1887, zatímco Schröderovo jméno je často vynecháno, protože jeho důkaz se ukázal být chybný, zatímco jméno Richard Dedekind , který to poprvé dokázal, není s větou spojen. Podle Bernsteina navrhl Cantor název věta o ekvivalenci (Äquivalenzsatz).

Cantorovo první prohlášení o větě (1887)

• 1887 Cantor vydává větu, ale bez důkazu.
• 1887 11. července Dedekind tuto větu dokazuje (nespoléhá na zvolený axiom ), ale nezveřejňuje svůj důkaz ani o něm Cantorovi neříká. Ernst Zermelo objevil Dedekindův důkaz a v roce 1908 vydává vlastní důkaz založený na řetězové teorii z Dedekindova papíru Byl sind und was sollen die Zahlen?
• 1895 Cantor uvádí větu ve svém prvním příspěvku o teorii množin a transfinitních číslech. Získává ho jako snadný důsledek lineárního pořadí světových čísel. Nicméně, nemohl dokázat druhou větu, která je znázorněna v roce 1915, aby bylo ekvivalentní k axiomu výběru ze strany Friedrich Moritz Hartogs .
• 1896 Schröder oznamuje důkaz (jako důsledek věty Jevons ).
• 1897 Bernstein , 19letý student Cantorova semináře, předkládá svůj důkaz.
• 1897 Téměř současně, ale nezávisle, Schröder najde důkaz.
• 1897 Po návštěvě Bernsteina Dedekind nezávisle potvrzuje větu podruhé.
• 1898 Bernsteinův důkaz (nespoléhající se na axiom volby) je publikován Émile Borelem v jeho knize o funkcích. (Sdělen Cantorem na Mezinárodním kongresu matematiků v Curychu 1897. ) Ve stejném roce se důkaz objevuje i v Bernsteinově disertaci.
• 1898 Schröder vydává svůj důkaz, který však Alwin Reinhold Korselt v roce 1902 (těsně před Schröderovou smrtí) (potvrzeno Schröderem) ukazuje jako chybný , ale Korseltův papír vychází až v roce 1911.

Oba Dedekindovy důkazy vycházejí z jeho slavné monografie z roku 1888 Byl sind und was sollen die Zahlen? a odvodit to jako důsledek výroku ekvivalentního tvrzení C v Cantorově článku, který zní A  ⊆  B  ⊆  C a | A | = | C | implikuje | A | = | B | = | C |. Cantor tuto vlastnost pozoroval již v letech 1882/83 během studií teorie množin a transfinitních čísel, a proto se (implicitně) spoléhal na Axiom of Choice .

Předpoklady

1895 důkaz pomocí Cantor opírala v podstatě o axiom výběru tím odvozovat výsledek jako důsledek tohoto zermelova věta . Výše uvedený Königův důkaz však ukazuje, že výsledek lze také dokázat bez použití zvoleného axiomu.

Na druhé straně, Königův důkaz používá princip vyloučeného středu , aby provedl analýzu případů, takže tento důkaz nefunguje v konstruktivní teorii množin . A co víc, nemůže existovat žádný důkaz pouze z konstruktivní teorie množin (tj. Bez principu vyloučeného středu), protože Schröder – Bernsteinova věta implikuje princip vyloučeného středu. Proto intuitionists nepřijímají větu.

Existuje také důkaz, který používá Tarského teorém o pevných bodech .

Viz také

• Myhillova izomorfistická věta
• Schröder – Bernsteinova věta pro měřitelné prostory
• Schröder – Bernsteinovy ​​věty pro algebry operátorů
• Vlastnost Schröder – Bernstein

Poznámky

Reference

• Martin Aigner & Gunter M. Ziegler (1998) Důkazy z KNIHY , § 3 Analýza: Sady a funkce, Springerovy knihy MR 1723092 , páté vydání 2014 MR 3288091 , šesté vydání 2018 MR 3823190
• Hinkis, Arie (2013), Důkazy o Cantor-Bernsteinově větě. Matematická exkurze , Vědecké sítě. Historical Studies, 45 , Heidelberg: Birkhäuser/Springer, doi : 10.1007/978-3-0348-0224-6 , ISBN 978-3-0348-0223-9, MR  3026479
• Searcóid, Míchaél Ó (2013). „K historii a matematice věty o ekvivalenci“. Matematický sborník Královské irské akademie . 113A : 151–68. doi : 10.3311/PRIA.2013.113.14 . JSTOR  42912521 .

externí odkazy

• Weisstein, Eric W. „Schröder-Bernsteinova věta“ . MathWorld .
• Cantor-Schroeder-Bernsteinova věta v nLab
• Cantor-Bernsteinova věta v Semiring od Marcela Crabbého.
• Tento článek včlení materiál z článku Citizendium „ Schröder-Bernstein_theorem “, který je licencován pod neportovanou licencí Creative Commons Attribution-ShareAlike 3.0, ale nikoli pod GFDL .