Vesmírná skupina - Space group

Prostor skupina hexagonální H ₂ O ledu je P6 ₃ / MMC . První m označuje rovinu zrcadlení kolmou k ose c (a), druhá m označuje roviny zrcadlení rovnoběžné s osou c (b) a c označuje roviny klouzání (b) a (c). Černé rámečky obkreslují buňku jednotky.

V matematiky , fyziky a chemie , je prostorová skupina je skupina symetrie objektu v prostoru, obvykle ve třech rozměrech . Prvky vesmírné skupiny (její operace symetrie ) jsou rigidní transformace objektu, který jej ponechává beze změny. Ve třech dimenzích jsou vesmírné skupiny rozděleny do 219 odlišných typů nebo 230 typů, pokud jsou chirální kopie považovány za odlišné. Prostor skupiny jsou diskrétní cocompact skupiny z isometries orientovaného euklidovském prostoru v jakémkoli počtu rozměrů. V jiných dimenzích než 3 se jim někdy říká skupiny Bieberbach .

V krystalografii se vesmírné skupiny nazývají také krystalografické nebo Fedorovovy skupiny a představují popis symetrie krystalu. Definitivní zdroj týkající se 3-dimenzionálních prostorových skupin je Mezinárodní tabulky pro krystalografii Hahn (2002) .

Dějiny

Vesmírné skupiny ve 2 rozměrech jsou 17 skupin tapet, které jsou známy již několik století, ačkoli důkaz, že seznam byl úplný, byl poskytnut až v roce 1891, poté, co byla do značné míry dokončena mnohem obtížnější klasifikace vesmírných skupin.

V roce 1879 německý matematik Leonhard Sohncke uvedl 65 vesmírných skupin (nazývaných Sohnckeovy skupiny), jejichž prvky zachovávají chiralitu . Přesněji uvedl 66 skupin, ale jak ruský matematik a krystalograf Evgraf Fedorov, tak německý matematik Arthur Moritz Schoenflies si všimli, že dvě z nich jsou opravdu stejné. Prostorové skupiny ve třech rozměrech poprvé vyjmenoval v roce 1891 Fedorov (jehož seznam měl dvě opomenutí (I 4 3d a Fdd2) a jednu duplikaci (Fmm2)), a krátce nato v roce 1891 byly samostatně vyčísleny Schönfliesem (jehož seznam měl čtyři opomenutí) (I 4 3d, Pc, Cc,?) A jedna duplikace (P 4 2 ₁ m)). Správný seznam 230 vesmírných skupin byl nalezen v roce 1892 během korespondence mezi Fedorovem a Schönfliesem. Barlow ( 1894 ) později vyjmenoval skupiny jinou metodou, ale vynechal čtyři skupiny (Fdd2, I 4 2d, P 4 2 ₁ d a P 4 2 ₁ c), přestože už měl správný seznam 230 skupin od Fedorova a Schönflies; společné tvrzení, že Barlow o jejich práci nevěděl, je nesprávné. Burckhardt (1967) podrobně popisuje historii objevu vesmírných skupin.

Elementy

Prostorové skupiny ve třech rozměrech jsou vytvořeny z kombinací 32 krystalografických skupin bodů se 14 mřížkami Bravais , z nichž každá patří do jednoho ze 7 mřížových systémů . To znamená, že působení jakéhokoli prvku dané prostorové skupiny lze vyjádřit jako působení prvku příslušné bodové skupiny následované volitelně překladem. Prostorová skupina je tedy určitá kombinace translační symetrie jednotkové buňky (včetně centrování mřížky ), operací symetrie bodové skupiny odrazu , rotace a nesprávné rotace (také nazývané rotační inverze) a operací symetrie osy šroubu a roviny klouzání . Výsledkem kombinace všech těchto operací symetrie je celkem 230 různých prostorových skupin popisujících všechny možné krystalické symetrie.

Prvky upevňující bod

Prvky skupiny prostorů fixující bod prostoru jsou element identity, odrazy, rotace a nesprávné rotace .

Překlady

Překlady tvoří normální abelianskou podskupinu 3. úrovně , nazývanou Bravaisova mříž. Existuje 14 možných typů mřížky Bravais. Kvocient z prostorové skupiny podle Bravais mříží je konečná skupina, která je jednou z možných 32 bodových skupin .

Kluzná letadla

Plachtit letadlo je odrazem v rovině, následuje překlad paralelně s touto rovinou. To je známý tím , nebo , v závislosti na ose kluzné je spolu. Existuje také klouzání, což je klouzání po polovině úhlopříčky obličeje, a klouzání, které je ve čtvrtině cesty buď po obličejové nebo prostorové úhlopříčce jednotkové buňky. Ten se nazývá diamantová rovina klouzání, protože je součástí diamantové struktury. V 17 vesmírných skupinách se v důsledku centrování buňky klouzání vyskytuje ve dvou kolmých směrech současně, tj. Stejná rovina skluzu může být nazývána b nebo c , a nebo b , a nebo c . Skupinu Abm2 lze například také nazývat Acm2, skupinu Ccca lze nazvat Cccb. V roce 1992 bylo navrženo použít pro takové letouny symbol e . Byly upraveny symboly pro pět skupin prostorů: ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle c}$ ${\ displaystyle n}$ ${\ displaystyle d}$

Vesmírná skupina č.	39	41	64	67	68
Nový symbol	Aem2	Aea2	Cmce	Cmme	Ccce
Starý symbol	Abm2	Aba2	Cmca	Cmma	Ccca

Šroubové sekery

Osa šroubu je rotace kolem osy, po kterém následuje posun podél směru osy. Ty jsou označeny číslem, n , popisujícím stupeň otáčení, kde číslo udává, kolik operací musí být použito k dokončení úplného otočení (např. 3 by znamenalo otočení pokaždé o jednu třetinu cesty kolem osy) . Stupeň translace se poté sečte jako dolní index ukazující, jak daleko podél osy je překlad, jako část vektoru paralelní mřížky. 2 ₁ je tedy dvojnásobná rotace následovaná překladem 1/2 vektoru mřížky.

Obecný vzorec

Obecný vzorec pro působení prvku vesmírné skupiny je

y = M . x + D

kde M je jeho matice, D je jeho vektor a kde prvek transformuje bod x na bod y . Obecně platí, že D = D ( mřížka ) + D ( M ), kde D ( M ) je jedinečná funkce M, která je nulová, protože M je identita. Matice M tvoří bodovou skupinu, která je základem prostorové skupiny; mřížka musí být pod touto bodovou skupinou symetrická, ale samotná krystalová struktura nemusí být symetrická v rámci této bodové skupiny, jak je aplikována na jakýkoli konkrétní bod (tedy bez překladu). Například diamantová krychlová struktura nemá žádný bod, kde platí skupina kubických bodů .

Dimenze mřížky může být menší než celková dimenze, což má za následek „subperiodickou“ prostorovou skupinu. Pro (celkový rozměr, rozměr mřížky):

(1,1): Jednorozměrné skupiny čar
(2,1): Dvourozměrné řádkové skupiny : vlysové skupiny
(2,2): Skupiny tapet
(3,1): Trojrozměrné skupiny čar ; se skupinami 3D krystalografických bodů, tyčinkové skupiny
(3,2): Skupiny vrstev
(3,3): Vesmírné skupiny diskutované v tomto článku

Zápis

Existuje nejméně deset metod pojmenování skupin prostorů. Některé z těchto metod mohou téže vesmírné skupině přiřadit několik různých jmen, takže dohromady existuje mnoho tisíc různých jmen.

Číslo: Mezinárodní unie krystalografie vydává tabulky všech typů prostorových skupin a každé přiřazuje jedinečné číslo od 1 do 230. Číslování je libovolné, kromě toho, že skupinám se stejným krystalovým systémem nebo bodovou skupinou jsou přiřazována po sobě jdoucí čísla.

Mezinárodní symbolický zápis

Hermann – Mauguinova notace

Notace Hermann – Mauguin (nebo mezinárodní) popisuje mřížku a některé generátory pro skupinu. Má zkrácenou formu nazývanou mezinárodní krátký symbol , který je v krystalografii nejčastěji používán, a obvykle se skládá ze sady čtyř symbolů. První popisuje vycentrování Bravaisovy mřížky ( P , A , C , I , R nebo F ). Další tři popisují nejvýraznější operaci symetrie viditelnou při promítnutí podél jednoho ze směrů vysoké symetrie krystalu. Tyto symboly jsou stejné jako v bodových skupinách , s přidáním kluzných rovin a osy šroubu, popsaných výše. Prostorová skupina křemene je například P3 ₁ 21, což ukazuje, že vykazuje primitivní centrování motivu (tj. Jednou na jednotku buňky) s trojnásobnou osou šroubu a dvojnásobnou osou otáčení. Všimněte si, že výslovně neobsahuje krystalový systém , ačkoli toto je jedinečné pro každou skupinu prostorů (v případě P 3 ₁ 21 je to trigonální).

V mezinárodním krátkém symbolu první symbol ( v tomto případě 3 ₁ ) označuje symetrii podél hlavní osy (osa c v trigonálních případech), druhá (v tomto případě 2) podél os sekundárního významu (a a b) a třetí symbol symetrii v jiném směru. V trigonálním případě existuje také prostorová skupina P3 ₁ 12. V této prostorové skupině nejsou dvojí osy podél os a a b, ale ve směru otočeném o 30 °.

Mezinárodní symboly a mezinárodní krátké symboly pro některé z vesmírných skupin byly v letech 1935 až 2002 mírně změněny, takže několik vesmírných skupin používá 4 různé mezinárodní symboly.

Směr pohledu 7 krystalových systémů je zobrazen následovně.

Pozice v symbolu	Triclinic	Monoklinika	Orthorhombic	Tetragonální	Trigonální	Šestihranný	Krychlový
1	-	b	A	C	C	C	A
2	-		b	A	A	A	[111]
3	-		C	[110]	[210]	[210]	[110]

Hallův zápis: Zápis vesmírné skupiny s explicitním původem. Symboly otáčení, translace a směru os jsou jasně odděleny a inverzní centra jsou explicitně definována. Konstrukce a formát zápisu jej činí zvláště vhodným pro počítačové generování informací o symetrii. Například skupina číslo 3 má tři Hallovy symboly: P 2y (P 1 2 1), P 2 (P 1 1 2), P 2x (P 2 1 1).
Schönfliesova notace: Skupiny prostorů s danou skupinou bodů jsou očíslovány 1, 2, 3,… (ve stejném pořadí jako jejich mezinárodní číslo) a toto číslo je přidáno jako horní index k symbolu Schönflies pro skupinu bodů. Například skupiny čísla 3 až 5, jejichž bodovou skupinou je C _2, mají Schönfliesovy symboly C¹
₂, C.²
₂, C.³
₂.

Fedorovova notace

Symbol Shubnikov

Strukturbericht označení

Související zápis pro krystalické struktury s písmenem a indexem: Prvky A (monatomické), B pro sloučeniny AB, C pro sloučeniny AB ₂ , D pro sloučeniny A _m B _n , ( E , F , ..., K Složitější sloučeniny ), Slitiny L , O organické sloučeniny, S křemičitany. Některá označení struktury sdílejí stejné prostorové skupiny. Například skupina prostorů 225 je A ₁ , B ₁ a C ₁ . Vesmírná skupina 221 je A _h a B ₂ . Krystalografové by však k popisu vesmírné skupiny nepoužívali Strukturberichtovu notaci, spíše by byla použita k popisu konkrétní krystalové struktury (např. Vesmírná skupina + atomové uspořádání (motiv)).

Orbifold notace (2D)

Fibrifold notace (3D)

Jak naznačuje název, orbifold notace popisuje orbifold, daný kvocientem euklidovského prostoru vesmírnou skupinou, spíše než generátory vesmírné skupiny. Byl představen Conwayem a Thurstonem a mimo matematiku se příliš nepoužívá. K některým vesmírným skupinám je přidruženo několik různých fibrifoldů, takže má několik různých symbolů fibrifold.

Coxeterova notace: Skupiny prostorové a bodové symetrie, reprezentované jako modifikace čistě reflexních Coxeterových skupin .
Geometrický zápis: Zápis geometrické algebry .

Klasifikační systémy

Existuje (minimálně) 10 různých způsobů, jak klasifikovat skupiny prostorů do tříd. Vztahy mezi některými z nich jsou popsány v následující tabulce. Každý klasifikační systém je zdokonalením těch pod ním.

(Krystalografické) typy skupin prostorů (230 ve třech rozměrech)
Dvě vesmírné skupiny, považované za podskupiny skupiny afinních transformací prostoru, mají stejný typ vesmírných skupin, pokud jsou konjugovány afinní transformací zachovávající chiralitu. Ve třech dimenzích neexistuje pro 11 afinních vesmírných skupin žádná mapa pro zachování chirality od skupiny k jejímu zrcadlovému obrazu, takže pokud člověk rozlišuje skupiny od svých zrcadlových obrazů, každý se rozdělí na dva případy (jako P4 ₁ a P4 ₃ ). Existuje tedy 54 + 11 = 65 typů prostorových skupin, které zachovávají chiralitu (skupiny Sohncke).
Afinní typy vesmírných skupin (219 ve třech rozměrech)
Dvě vesmírné skupiny, považované za podskupiny skupiny afinních transformací prostoru, mají stejný typ afinních prostorových skupin, pokud jsou konjugované pod afinní transformací. Typ afinní prostorové skupiny je určen základní abstraktní skupinou vesmírné skupiny. Ve třech dimenzích existuje 54 typů afinních vesmírných skupin, které zachovávají chiralitu.
Aritmetické třídy krystalů (73 ve třech rozměrech)
Někdy se jim říká třídy Z. Ty jsou určeny bodovou skupinou společně s působením bodové skupiny na podskupinu překladů. Jinými slovy, třídy aritmetických krystalů odpovídají třídám konjugace konečné podskupiny obecné lineární skupiny GL _n ( Z ) přes celá čísla. Prostorová skupina se nazývá symmorfní (nebo rozdělená ), pokud existuje takový bod, že všechny symetrie jsou výsledkem symetrie, která tento bod fixuje, a překladu. Ekvivalentně je prostorová skupina symmorfní, pokud je polopřímým produktem její bodové skupiny s její podskupinou překladu. Existuje 73 symmorfních prostorových skupin, přičemž v každé třídě aritmetických krystalů je přesně jedna. Existuje také 157 nesymmorfních typů prostorových skupin s různým počtem v aritmetických krystalových třídách. Aritmetické třídy krystalů lze interpretovat jako různé orientace bodových skupin v mřížce, přičemž maticové složky skupinových prvků jsou omezeny tak, aby měly v mřížkovém prostoru celočíselné koeficienty. To je docela snadné si představit v případě dvourozměrného případu skupiny tapet . Některé z bodových skupin mají odrazy a odrazové čáry mohou být ve směru mřížky, v polovině mezi nimi nebo v obou. Žádný: C ₁ : p1; C ₂ : p2; C ₃ : P3; C ₄ : p4; C ₆ : p6 Podél: D ₁ : pm, str; D ₂ : pmm, pmg, pgg; D ₃ : p31m Mezi: D ₁ : cm; D ₂ : cmm; D ₃ : p3m1 Oba: D ₄ : p4m, p4g; D ₆ : p6m
(geometrické) Krystalové třídy (32 ve třech rozměrech)	Hejna Bravais (14 ve třech rozměrech)
Někdy se jim říká Q-třídy. Krystalová třída prostorové skupiny je určena její bodovou skupinou: kvocient podskupinou překladů, působícími na mřížku. Dvě prostorové skupiny jsou ve stejné třídě krystalů tehdy a jen tehdy, pokud jejich bodové skupiny, které jsou podskupinami GL _n ( Z ), je konjugát ve větší skupině GL _n ( Q ).	Ty jsou určeny základním typem mřížky Bravais. Ty odpovídají třídám konjugace skupin bodů mřížky v GL _n ( Z ), kde skupina bodů mřížky je skupina symetrií podkladové mřížky, která fixuje bod mřížky, a obsahuje skupinu bodů.
Krystalové systémy (7 ve třech rozměrech)	Příhradové systémy (7 ve třech rozměrech)
Krystalové systémy jsou ad hoc modifikací mřížkových systémů, aby byly kompatibilní s klasifikací podle bodových skupin. Liší se od krystalových rodin v tom, že hexagonální krystalová rodina je rozdělena do dvou podmnožin, nazývaných trigonální a hexagonální krystalové systémy. Trigonální krystalový systém je větší než romboedrický mřížkový systém, hexagonální krystalový systém je menší než hexagonální mřížkový systém a zbývající krystalové systémy a mřížkové systémy jsou stejné.	Mřížkový systém prostorové skupiny je určen třídou konjugace skupiny mřížkových bodů (podskupina GL _n ( Z )) ve větší skupině GL _n ( Q ). Ve třech rozměrech může mít skupina mřížových bodů jeden ze 7 různých řádů 2, 4, 8, 12, 16, 24 nebo 48. Rodina hexagonálních krystalů je rozdělena do dvou podmnožin, nazývaných romboedrické a hexagonální mřížkové systémy.
Krystalové rodiny (6 ve třech rozměrech)
Bodová skupina prostorové skupiny zcela neurčuje její mřížkový systém, protože příležitostně mohou být dvě prostorové skupiny se stejnou bodovou skupinou v různých mřížkových systémech. Rodiny krystalů se vytvářejí z mřížových systémů sloučením obou mřížkových systémů, kdykoli se to stane, takže krystalová rodina prostorové skupiny je určena buď její mřížkovou soustavou, nebo její bodovou skupinou. Ve 3 rozměrech jsou jedinými dvěma mřížkovými rodinami, které se tímto způsobem spojily, šestihranné a romboedrické mřížkové systémy, které jsou sloučeny do rodiny hexagonálních krystalů. 6 krystalových rodin ve 3 rozměrech se nazývá triklinické, monoklinické, ortorombické, tetragonální, hexagonální a krychlové. Krystalové rodiny se běžně používají v populárních knihách o krystalech, kde se jim někdy říká krystalový systém.

Conway , Delgado Friedrichs a Huson et al. ( 2001 ) poskytli další klasifikaci prostorových skupin, nazývanou fibrifoldová notace , podle struktur fibrifold na odpovídajícím orbifoldu . Rozdělili 219 afinních vesmírných skupin na redukovatelné a neredukovatelné skupiny. Redukovatelné skupiny spadají do 17 tříd odpovídajících 17 skupinám tapet a zbývajících 35 neredukovatelných skupin je stejných jako kubické skupiny a jsou klasifikovány samostatně.

V jiných rozměrech

Bieberbachovy věty

V n dimenzích je skupina afinního prostoru nebo Bieberbachova skupina diskrétní podskupinou izometrií n -dimenzionálního euklidovského prostoru s kompaktní základní doménou. Bieberbach ( 1911 , 1912 ) dokázal, že podskupina překladů jakékoli takové skupiny obsahuje n lineárně nezávislých překladů a je volnou abelskou podskupinou konečného indexu a je také jedinečnou maximální normální abelskou podskupinou. Ukázal také, že v jakékoli dimenzi n existuje pouze konečný počet možností pro třídu izomorfismu základní skupiny vesmírné skupiny a navíc působení skupiny na euklidovský prostor je jedinečné až do konjugace afinními transformacemi. To odpovídá části Hilbertova osmnáctého problému . Zassenhaus (1948) ukázal, že naopak každá skupina, která je rozšířením Z ⁿ o konečnou skupinu jednající věrně, je afinní vesmírná skupina. Kombinace těchto výsledků ukazuje, že klasifikace prostorových skupin v n dimenzích až do konjugace afinními transformacemi je v podstatě stejná jako klasifikace tříd izomorfismu pro skupiny, které jsou rozšířením Z ⁿ konečnou skupinou, která působí věrně.

V Bieberbachových větách je zásadní předpokládat, že skupina funguje jako izometrie; věty negeneralizují na diskrétní kokompaktní skupiny afinních transformací euklidovského prostoru. Protipříklad je dán 3-dimenzionální Heisenbergovou skupinou celých čísel působících překlady na Heisenbergovu skupinu realit, identifikovanou s 3-dimenzionálním euklidovským prostorem. Toto je diskrétní souběžná skupina afinních transformací prostoru, ale neobsahuje podskupinu Z ³ .

Klasifikace v malých rozměrech

Tato tabulka uvádí počet typů prostorových skupin v malých rozměrech, včetně počtu různých tříd vesmírných skupin. Počty enantiomorfních párů jsou uvedeny v závorkách.

Rozměry	Krystalické rodiny, sekvence OEIS A004032	Krystalové systémy, sekvence OEIS A004031	Bravaisovy mříže, sekvence OEIS A256413	Abstraktní krystalografické skupiny bodů, sekvence OEIS A006226	Geometrické třídy krystalů, třídy Q, skupiny krystalografických bodů, sekvence OEIS A004028	Aritmetické třídy krystalů, třídy Z, sekvence OEIS A004027	Typy afinních vesmírných skupin, sekvence OEIS A004029	Krystalografické typy prostorových skupin, sekvence OEIS A006227
0	1	1	1	1	1	1	1	1
1	1	1	1	2	2	2	2	2
2	4	4	5	9	10	13	17	17
3	6	7	14	18	32	73	219 (+11)	230
4	23 (+6)	33 (+7)	64 (+10)	118	227 (+44)	710 (+70)	4783 (+111)	4894
5	32	59	189	239	955	6079	222018 (+79)	222097
6	91	251	841	1594	7103	85308 (+?)	28927915 (+?)	?

Magnetické skupiny a obrácení času

Kromě krystalografických prostorových skupin existují ještě magnetické prostorové skupiny (nazývané také dvoubarevné (černé a bílé) krystalografické skupiny nebo Shubnikovovy skupiny). Tyto symetrie obsahují prvek známý jako obrácení času. Zacházejí s časem jako s další dimenzí a prvky skupiny mohou zahrnovat zvrat času jako odraz v něm. Jsou důležité v magnetických strukturách, které obsahují uspořádané nepárové spiny, tj. Ferro- , ferri- nebo antiferomagnetické struktury, jak byly studovány neutronovou difrakcí . Prvek časového převrácení převrací magnetický spin, přičemž všechny ostatní struktury zůstávají stejné a lze jej kombinovat s řadou dalších prvků symetrie. Včetně časového obrácení existuje 1651 skupin magnetického prostoru ve 3D ( Kim 1999 , s. 428). Rovněž bylo možné zkonstruovat magnetické verze pro jiné celkové a mřížkové rozměry ( papíry Daniela Litvina , ( Litvin 2008 ), ( Litvin 2005 )). Skupiny vlysu jsou magnetické 1D řádkové skupiny a skupiny vrstev jsou magnetické tapety a axiální 3D bodové skupiny jsou magnetické 2D bodové skupiny. Počet původních a magnetických skupin podle (celkové, mřížkové) dimenze :( Palistrant 2012 ) ( Souvignier 2006 )

Celkový rozměr	Mřížkový rozměr	Obyčejné skupiny			Magnetické skupiny
Celkový rozměr	Mřížkový rozměr	název	Symbol	Počet	Symbol	Počet
0	0	Skupina nulové dimenze symetrie	${\ displaystyle G_ {0}}$	1	${\ displaystyle G_ {0}^{1}}$	2
1	0	Jednorozměrné skupiny bodů	${\ displaystyle G_ {10}}$	2	${\ displaystyle G_ {10}^{1}}$	5
1	1	Jednorozměrné diskrétní skupiny symetrie	${\ displaystyle G_ {1}}$	2	${\ displaystyle G_ {1}^{1}}$	7
2	0	Dvourozměrné skupiny bodů	${\ displaystyle G_ {20}}$	10	${\ displaystyle G_ {20}^{1}}$	31
	1	Skupiny vlysu	${\ displaystyle G_ {21}}$	7	${\ displaystyle G_ {21}^{1}}$	31
	2	Skupiny tapet	${\ displaystyle G_ {2}}$	17	${\ displaystyle G_ {2}^{1}}$	80
3	0	Trojrozměrné skupiny bodů	${\ displaystyle G_ {30}}$	32	${\ displaystyle G_ {30}^{1}}$	122
	1	Skupiny prutů	${\ displaystyle G_ {31}}$	75	${\ displaystyle G_ {31}^{1}}$	394
	2	Skupiny vrstev	${\ displaystyle G_ {32}}$	80	${\ displaystyle G_ {32}^{1}}$	528
	3	Trojrozměrné vesmírné skupiny	${\ displaystyle G_ {3}}$	230	${\ displaystyle G_ {3}^{1}}$	1651
4	0	Čtyřrozměrné skupiny bodů	${\ displaystyle G_ {40}}$	271	${\ displaystyle G_ {40}^{1}}$	1202
	1		${\ displaystyle G_ {41}}$	343
	2		${\ displaystyle G_ {42}}$	1091
	3		${\ displaystyle G_ {43}}$	1594
	4	Skupiny čtyřrozměrných diskrétních symetrií	${\ displaystyle G_ {4}}$	4894	${\ displaystyle G_ {4}^{1}}$	62227

Tabulka skupin prostorů ve 2 rozměrech (skupiny tapet)

Tabulka skupin tapet pomocí klasifikace skupin trojrozměrných prostorů:

Krystalový systém , Bravaisova mříž	Geometrická třída, bodová skupina				Aritmetická třída	Skupiny tapet (diagram buněk)
Krystalový systém , Bravaisova mříž	Schön.	Orbifold	Kormidelník.	Obj.	Aritmetická třída	Skupiny tapet (diagram buněk)
Šikmý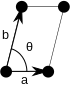	C ₁	(1)	[] ⁺	1	Žádný	p1 (1)
Šikmý	C ₂	(22)	[2] ⁺	2	Žádný	p2 (2222)
Obdélníkový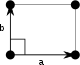	D ₁	(*)	[]	2	Podél	pm (**)	str (× ×)
Obdélníkový	D ₂	(*22)	[2]	4	Podél	pmm (*2222)	pmg (22*)
Vycentrovaný obdélník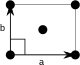	D ₁	(*)	[]	2	Mezi	cm (*×)
Vycentrovaný obdélník	D ₂	(*22)	[2]	4	Mezi	cmm (2*22)	pgg (22 ×)
Náměstí	C ₄	(44)	[4] ⁺	4	Žádný	p4 (442)
Náměstí	D ₄	(*44)	[4]	8	Oba	p4m (*442)	p4g (4*2)
Šestihranný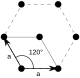	C ₃	(33)	[3] ⁺	3	Žádný	p3 (333)
	D ₃	(*33)	[3]	6	Mezi	p3m1 (*333)	p31m (3*3)
	C ₆	(66)	[6] ⁺	6	Žádný	p6 (632)
	D ₆	(*66)	[6]	12	Oba	p6m (*632)

Pro každou geometrickou třídu jsou možné aritmetické třídy

Žádné: žádné odrazové čáry
Podél: reflexní čáry podél směrů mříže
Mezi: reflexní čáry uprostřed mezi směry mřížky
Oba: reflexní čáry podél i mezi směry mřížek

Tabulka skupin prostorů ve 3 rozměrech

#	Krystalový systém , (počet), Bravaisova mříž	Bodová skupina					Vesmírné skupiny (mezinárodní krátký symbol)
#	Krystalový systém , (počet), Bravaisova mříž	Int'l	Schön.	Orbifold	Kormidelník.	Obj.	Vesmírné skupiny (mezinárodní krátký symbol)
1	Triclinic (2)	1	C ₁	11	[] ⁺	1	P1
2	Triclinic (2)	1	C _i	1 ×	[2 ⁺ , 2 ⁺ ]	2	P 1
3–5	Monoklinika (13)	2	C ₂	22	[2] ⁺	2	P2, P2 ₁ C2
6–9		m	C _s	*11	[]	2	Pm, Pc Cm, Cc
10–15		2/m	C _2h	2*	[2,2 ⁺ ]	4	P2/m, P2 ₁ /m C2/m, P2/c, P2 ₁ /c C2/c
16–24	Orthorhombic (59)	222	D ₂	222	[2,2] ⁺	4	P222, P222 ₁ , P2 ₁ 2 ₁ 2, P2 ₁ 2 ₁ 2 ₁ , C222 ₁ , C222, F222, I222, I2 ₁ 2 ₁ 2 ₁
25–46		mm2	C _2v	*22	[2]	4	Pmm2, Pmc2 ₁ , Pcc2, Pma2, Pca2 ₁ , Pnc2, Pmn2 ₁ , Pba2, Pna2 ₁ , Pnn2 Cmm2, Cmc2 ₁ , Ccc2, Amm2, Aem2, Ama2, Aea2 Fmm2, Fdd2 Imm2, Iba2, Ima2
47–74		mmm	D _2h	*222	[2,2]	8	Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma Cmcm, Cmce, Cmmm, Cccm, Cmme, Ccce Fmmm, Fdd Im "Imma."
75–80	Tetragonal (68)	4	C ₄	44	[4] ⁺	4	P4, P4 ₁ , P4 ₂ , P4 ₃ , I4, I4 ₁
81–82		4	S ₄	2 ×	[2 ⁺ , 4 ⁺ ]	4	P 4 , I 4
83–88		4/m	C _4h	4*	[2,4 ⁺ ]	8	P4 /m, P4 ₂ /m, P4 /n, P4 ₂ /n I4 /m, I4 ₁ /a
89–98		422	D ₄	224	[2,4] ⁺	8	P422, P42 ₁ 2, P4 ₁ 22, P4 ₁ 2 ₁ 2, P4 ₂ 22, P4 ₂ 2 ₁ 2, P4 ₃ 22, P4 ₃ 2 ₁ 2 I422, I4 ₁ 22
99–110		4 mm	C _4v	*44	[4]	8	P4mm, P4bm, P4 ₂ cm, P4 ₂ nm, P4cc, P4nc, P4 ₂ mc, P4 ₂ bc I4mm, I4cm, I4 ₁ md, I4 ₁ cd
111–122		4 2m	D _2d	2*2	[2 ⁺ , 4]	8	P 4 2m, P 4 2c, P 4 2 ₁ m, P 4 2 ₁ c, P 4 m2, P 4 c2, P 4 b2, P 4 n2 I 4 m2, I 4 c2, I 4 2m, I 4 2d
123–142		4/mmm	D _4h	*224	[2,4]	16	P4/mmm, P4/mcc, P4/nbm, P4/nnc, P4/mbm, P4/mnc, P4/nmm, P4/ncc, P4 ₂ /mmc, P4 ₂ /mcm, P4 ₂ /nbc, P4 ₂ / nnm, P4 ₂ /mbc, P4 ₂ /mnm, P4 ₂ /nmc, P4 ₂ /ncm I4 /mmm, I4 /mcm, I4 ₁ /amd, I4 ₁ /acd
143–146	Trigonální (25)	3	C ₃	33	[3] ⁺	3	P3, P3 ₁ , P3 ₂ R3
147–148		3	S ₆	3 ×	[2 ⁺ , 6 ⁺ ]	6	P 3 , R 3
149–155		32	D ₃	223	[2,3] ⁺	6	P312, P321, P3 ₁ 12, P3 ₁ 21, P3 ₂ 12, P3 ₂ 21 R32
156–161		3 m	C _3v	*33	[3]	6	P3m1, P31m, P3c1, P31c R3m, R3c
162–167		3 m	D _3d	2*3	[2 ⁺ , 6]	12	P 3 1m, P 3 1c, P 3 m1, P 3 c1 R 3 m, R 3 c
168–173	Šestihranný (27)	6	C ₆	66	[6] ⁺	6	P6, P6 ₁ , P6 ₅ , P6 ₂ , P6 ₄ , P6 ₃
174		6	C _3h	3*	[2,3 ⁺ ]	6	P 6
175–176		6/m	C _6h	6*	[2,6 ⁺ ]	12	P6 /m, P6 ₃ /m
177–182		622	D ₆	226	[2,6] ⁺	12	P622, P6 ₁ 22, P6 ₅ 22, P6 ₂ 22, P6 ₄ 22, P6 ₃ 22
183–186		6 mm	C _6v	*66	[6]	12	P6mm, P6cc, P6 ₃ cm, P6 ₃ mc
187–190		6 m2	D _3h	*223	[2,3]	12	P 6 m2, P 6 c2, P 6 2m, P 6 2c
191–194		6/mmm	D _6h	*226	[2,6]	24	P6 /mmm, P6 /mcc, P6 ₃ /mcm, P6 ₃ /mmc
195–199	Krychlový (36)	23	T	332	[3,3] ⁺	12	P23, F23, I23 P2 ₁ 3, I2 ₁ 3
200–206		m 3	T _h	3*2	[3 ⁺ , 4]	24	Pm 3 , Pn 3 , Fm 3 , Fd 3 , Im 3 , Pa 3 , Ia 3
207–214		432	Ó	432	[3,4] ⁺	24	P432, P4 ₂ 32 F432, F4 ₁ 32 I432 P4 ₃ 32, P4 ₁ 32, I4 ₁ 32
215–220		4 3m	T _d	*332	[3,3]	24	P 4 3m, F 4 3m, I 4 3m P 4 3n, F 4 3c, I 4 3d
221–230		m 3 m	O _h	*432	[3,4]	48	Pm 3 m, Pn 3 n, Pm 3 n, Pn 3 m Fm 3 m, Fm 3 c, Fd 3 m, Fd 3 c Im 3 m, Ia 3 d

Poznámka: Rovina e je dvojitá kluzná rovina, která má klouzání ve dvou různých směrech. Nacházejí se v sedmi ortorombických, pěti tetragonálních a pěti kubických vesmírných skupinách, všechny se středovou mřížkou. Použití symbolu e se stalo oficiálním u Hahna (2002) .

Mřížkový systém lze nalézt následovně. Pokud krystalový systém není trigonální, pak je mřížkový systém stejného typu. Pokud je krystalový systém trigonální, pak je mřížkový systém šestihranný, pokud není prostorová skupina jednou ze sedmi v kosočtvercovém mřížkovém systému, který se skládá ze 7 skupin trigonálních prostorů v tabulce, jejíž název začíná na R. (Termín kosočtverečný systém je někdy také používán jako alternativní název pro celý trigonální systém.) Šestihranný mřížkový systém je větší než šestihranný krystalový systém a skládá se ze šestihranného krystalového systému společně s 18 skupinami jiných trojúhelníkových krystalových systémů než sedmi, jejichž jména začínají s R.

Bravais mříž z prostorové grupy je určen mřížky systému společně s počátečním písmenem jeho jména, která je pro non-romboedrických skupin P, I, F, A nebo C, stání pro hlavní, centrované, plošně centrovanou , Mříže se středem ve tvaru písmene A nebo C s obličejem. Existuje sedm kosočtvercových vesmírných skupin s počátečním písmenem R.

Odvození třídy krystalů z vesmírné skupiny

Vynechejte typ Bravais
Převést všechny prvky symetrie s translačními komponentami na jejich příslušné prvky symetrie bez translační symetrie (Kluzné roviny jsou převedeny na jednoduché zrcadlové roviny; Osy šroubů jsou převedeny na jednoduché osy otáčení)
Osy otáčení, rotační osy a zrcadlové roviny zůstávají nezměněny.

Reference

Barlow, W (1894), „Über die geometrischen Eigenschaften starrer Strukturen und ihre Anwendung auf Kristalle“ [O geometrických vlastnostech tuhých struktur a jejich aplikaci na krystaly], Zeitschrift für Kristallographie , 23 : 1–63, doi : 10,1524/zkri .1894.23.1.1 , S2CID 102301331
Bieberbach, Ludwig (1911), „Über die Bewegungsgruppen der Euklidischen Räume“ [On the groups of rigid transformations in Euclidean spaces], Mathematische Annalen , 70 (3): 297–336, doi : 10.1007/BF01564500 , ISSN 0025-5831 , S2CID 124429194
Bieberbach, Ludwig (1912), „Über die Bewegungsgruppen der Euklidischen Räume (Zweite Abhandlung.) Die Gruppen mit einem endlichen Fundamentalbereich“ [O skupinách rigidních transformací v euklidovských prostorech (Druhá esej.) Skupiny s konečnou základní doménou], Mathematische Annalen , 72 (3): 400–412, doi : 10,1007/BF01456724 , ISSN 0025-5831 , S2CID 119472023
Brown, Harold; Bülow, Rolf; Neubüser, Joachim; Wondratschek, Hans; Zassenhaus, Hans (1978), Krystalografické skupiny čtyřrozměrného prostoru , New York: Wiley-Interscience [John Wiley & Sons], ISBN 978-0-471-03095-9, MR 0484179
Burckhardt, Johann Jakob (1947), Die Bewegungsgruppen der Kristallographie [ Groups of Rigid Transformations in Crystallography ], Lehrbücher und Monographien aus dem Gebiete der exakten Wissenschaften (Učebnice a monografie z polí přesných věd), 13 , Verlag Birkh MR 0020553
Burckhardt, Johann Jakob (1967), "Zur Geschichte der Entdeckung der 230 Raumgruppen" [Z historie objevu kosmických skupin 230] archiv dějin exaktních věd , 4 (3): 235-246, doi : 10,1007 /BF00412962 , ISSN 0003-9519 , MR 0220837 , S2CID 121994079
Conway, John Horton ; Delgado Friedrichs, Olaf; Huson, Daniel H .; Thurston, William P. (2001), „O trojrozměrných vesmírných skupinách“ , Beiträge zur Algebra und Geometrie , 42 (2): 475–507, ISSN 0138-4821 , MR 1865535
Fedorov, ES (1891a), "Симметрія правильныхъ системъ фигуръ" [ Simmetriya pravil'nykh sistem figur , Symetrie běžných systémů číslice], Записки Императорского С.-Петербургского Минералогического Общества (Zapiski Imperatorskova Sankt Petersburgskova Mineralogicheskova Obshchestva, Proceedings of the Imperial Petrohradská mineralogická společnost) , 2. řada (v ruštině), 28 (2): 1–146
- Anglický překlad: Fedorov, ES (1971). Symetrie krystalů . Monografie Americké krystalografické asociace č. 7. Přeložili David a Katherine Harkerovi. Buffalo, NY: Americká krystalografická asociace. s. 50–131.
Fedorov, ES (1891b). „Симметрія на плоскости“ [ Simmetrija na ploskosti , symetrie v rovině]. Записки Императорского С.-Петербургского Минералогического Общества (Zapiski Imperatorskogo Sant-Petersburgskogo Mineralogicheskogo Obshchestva, Proceedings of the Imperial St. Petersburg Mineralogické Society) . 2. série (v ruštině). 28 : 345–390.
Hahn, Th. (2002), Hahn, Theo (ed.), International Tables for Crystallography, Volume A: Space Group Symmetry , International Tables for Crystallography, A (5th ed.), Berlin, New York: Springer-Verlag , doi : 10.1107/97809553602060000100 , ISBN 978-0-7923-6590-7
Hall, SR (1981), „Space-Group Notation with an Explicit Origin“, Acta Crystallographica A , 37 (4): 517–525, Bibcode : 1981AcCrA..37..517H , doi : 10,1107/s0567739481001228
Janssen, T .; Birman, JL; Dénoyer, F .; Koptsik, VA; Verger-Gaugry, JL; Weigel, D .; Yamamoto, A .; Abrahams, SC; Kopsky, V. (2002), „Zpráva podvýboru pro nomenklaturu n -dimenzionální krystalografie. II. Symboly pro třídy aritmetických krystalů, třídy Bravais a prostorové skupiny“, Acta Crystallographica A , 58 (Pt 6): 605–621 , doi : 10.1107/S010876730201379X , PMID 12388880
Kim, Shoon K. (1999), Skupinové teoretické metody a aplikace na molekuly a krystaly , Cambridge University Press , doi : 10,1017/CBO9780511534867 , ISBN 978-0-521-64062-6, MR 1713786 , S2CID 117849701
Litvin, DB (květen 2008), „Tabulky krystalografických vlastností skupin magnetického prostoru“, Acta Crystallographica A , 64 (Pt 3): 419–24, Bibcode : 2008AcCrA..64..419L , doi : 10.1107/S010876730800768X , PMID 18421131
Litvin, DB (květen 2005), „Tabulky vlastností magnetických subperiodických skupin“ (PDF) , Acta Crystallographica A , 61 (Pt 3): 382–5, Bibcode : 2005AcCrA..61..382L , doi : 10.1107/S010876730500406X , PMID 15846043
Neubüser, J .; Souvignier, B .; Wondratschek, H. (2002), „Opravy krystalografických skupin čtyřrozměrného prostoru od Browna a kol. (1978) [New York: Wiley and Sons]“, Acta Crystallographica A , 58 (Pt 3): 301, doi : 10.1107/S0108767302001368 , PMID 11961294
Opgenorth, J; Plesken, W; Schulz, T (1998), „Krystalografické algoritmy a tabulky“, Acta Crystallographica A , 54 (Pt 5): 517–531, doi : 10,1107/S010876739701547X
Palistrant, AF (2012), „Complete Scheme of Four-Dimension Crystallographic Symetry Groups“, Crystallography Reports , 57 (4): 471–477, Bibcode : 2012CryRp..57..471P , doi : 10.1134/S1063774512040104 , S2CID 95680790
Plesken, Wilhelm; Hanrath, W (1984), „Mříže šestidimenzionálního prostoru“, Math. Comp. , 43 (168): 573–587, doi : 10,1090/s0025-5718-1984-0758205-5
Plesken, Wilhelm; Schulz, Tilman (2000), „Počítání krystalografických skupin v nízkých rozměrech“ , Experimental Mathematics , 9 (3): 407–411, doi : 10,1080/10586458.2000.10504417 , ISSN 1058-6458 , MR 1795312 , S2CID 40588234
Schönflies, Arthur Moritz (1923), „Theorie der Kristallstruktur“ [Theory of Crystal Structure], Gebrüder Bornträger, Berlin.
Souvignier, Bernd (2003), „Enantiomorfismus krystalografických skupin ve vyšších dimenzích s výsledky v dimenzích až 6“, Acta Crystallographica A , 59 (3): 210–220, doi : 10,1107/S0108767303004161 , PMID 12714771
Souvignier, Bernd (2006), „Čtyřrozměrné skupiny magnetických bodů a prostoru“, Zeitschrift für Kristallographie , 221 : 77–82, Bibcode : 2006ZK .... 221 ... 77S , doi : 10.1524/zkri.2006.221. 1,77 , S2CID 99946564
Vinberg, E. (2001) [1994], „Krystalografická skupina“ , Encyklopedie matematiky , EMS Press
Zassenhaus, Hans (1948), „Über einen Algorithmus zur Bestimmung der Raumgruppen“ [O algoritmu pro určování vesmírných skupin], Commentarii Mathematici Helvetici , 21 : 117–141, doi : 10.1007/BF02568029 , ISSN 0010-2571 , MR 0024424 , S2CID 120651709

Languages

In other projects