Sférické harmonické - Spherical harmonics

V matematice a fyzikální vědy , sférické harmonické jsou speciální funkce definované na povrchu koule . Často se používají při řešení parciálních diferenciálních rovnic v mnoha vědních oblastech.

Protože sférické harmonické tvoří kompletní sadu ortogonálních funkcí a tedy ortonormální základnu , lze každou funkci definovanou na povrchu koule zapsat jako součet těchto sférických harmonických. To je podobné periodickým funkcím definovaným na kruhu, které lze vyjádřit jako součet kruhových funkcí (siny a kosiny) prostřednictvím Fourierovy řady . Stejně jako siny a kosiny v Fourierově řadě mohou být sférické harmonické organizovány (prostorovou) úhlovou frekvencí , jak je vidět v řadách funkcí na obrázku vpravo. Dále, sférické harmonické funkce základu pro ireducibilních reprezentace z tak (3) , na skupinu rotací ve třech rozměrech, a tak hrají ústřední roli v skupinové teoretické diskusi o SO (3).

Sférické harmonické vznikají řešením Laplaceovy rovnice ve sférických doménách. Funkce, které jsou řešením Laplaceovy rovnice, se nazývají harmonické. Navzdory svému jménu, sférických vzít jejich nejjednodušší formu v pravoúhlých souřadnic , kde lze definovat jako homogenní polynomy o stupeň v tomto poslouchat Laplace rovnice. Spojení se sférickými souřadnicemi vzniká okamžitě, pokud člověk pomocí homogenity extrahuje faktor radiální závislosti z výše uvedeného polynomu stupně ; zbývající faktor lze považovat za funkci sférických úhlových souřadnic a pouze nebo ekvivalentně z vektoru orientačních jednotek specifikovaného těmito úhly. V tomto nastavení je lze považovat za úhlovou část sady řešení Laplaceovy rovnice ve třech rozměrech a tento úhel pohledu je často brán jako alternativní definice. ${\ displaystyle \ ell}$${\ displaystyle (x, y, z)}$${\ displaystyle r^{\ ell}}$${\ displaystyle \ ell}$${\ displaystyle \ theta}$${\ Displaystyle \ varphi}$ ${\ displaystyle \ mathbf {r}}$

Specifická sada sférických harmonických, označovaná nebo , je známá jako Laplaceovy sférické harmonické, protože je poprvé představil Pierre Simon de Laplace v roce 1782. Tyto funkce tvoří ortogonální systém, a jsou tedy základní pro rozšíření obecné funkce na koule, jak je uvedeno výše. ${\ Displaystyle Y _ {\ ell}^{m} (\ theta, \ varphi)}$${\ displaystyle Y _ {\ ell}^{m} ({\ mathbf {r}})}$

Sférické harmonické jsou důležité v mnoha teoretických a praktických aplikacích, včetně reprezentace vícepólových elektrostatických a elektromagnetických polí , elektronových konfigurací , gravitačních polí , geoidů , magnetických polí planetárních těles a hvězd a záření kosmického mikrovlnného pozadí . V 3D počítačové grafice hrají sférické harmonické roli v celé řadě témat, včetně nepřímého osvětlení ( okolní okluze , globální osvětlení , předpočítaný přenos záření atd.) A modelování 3D tvarů.

Dějiny

Sférických byly nejprve zkoumány v souvislosti s newtonovské potenciálem o Newtonův gravitační zákon ve třech dimenzích. V roce 1782 Pierre-Simon de Laplace ve své Mécanique Céleste určil, že gravitační potenciál v bodě x spojený se sadou bodových hmot m _i umístěných v bodech x _i byl dán ${\ Displaystyle \ mathbb {R} ^{3} \ to \ mathbb {R}}$

${\ Displaystyle V (\ mathbf {x}) = \ sum _ {i} {\ frac {m_ {i}} {| \ mathbf {x} _ {i}-\ mathbf {x} |}}.}$

Každý výraz ve výše uvedeném součtu je individuálním newtonovským potenciálem pro bodovou hmotu. Těsně před touto dobou zkoumala Adrien-Marie Legendre rozšíření newtonovského potenciálu o mocninách r = | x | a r ₁ = | x ₁ | . Zjistil, že když r ≤ r _1, pak

${\ displaystyle {\ frac {1} {| \ mathbf {x} _ {1}-\ mathbf {x} |}} = P_ {0} (\ cos \ gamma) {\ frac {1} {r_ {1 }}}+P_ {1} (\ cos \ gamma) {\ frac {r} {r_ {1}^{2}}}+P_ {2} (\ cos \ gamma) {\ frac {r^{2 }} {r_ {1}^{3}}}+\ cdots}$

kde γ je úhel mezi vektory x a x ₁ . Funkce jsou Legendreovy polynomy a lze je odvodit jako speciální případ sférických harmonických. Následně ve své monografii z roku 1782 Laplace zkoumal tyto koeficienty pomocí sférických souřadnic, které představují úhel γ mezi x ₁ a x . ( Podrobnější analýzu viz Aplikace polynomů Legendre ve fyzice .) ${\ Displaystyle P_ {i}: [-1,1] \ to \ mathbb {R}}$

V roce 1867, William Thomson (Lord Kelvin) a Peter Guthrie Tait představili pevné sférické harmonické ve svém pojednání o přírodní filozofii a také poprvé zavedli název „sférických harmonických“ pro tyto funkce. Tyto pevné harmonické byly homogenní polynomiální řešení z Laplaceova rovnice${\ Displaystyle \ mathbb {R} ^{3} \ to \ mathbb {R}}$

${\ Displaystyle {\ frac {\ částečné ^{2} u} {\ částečné x ^{2}}}+{\ frac {\ částečné ^{2} u} {\ částečné y ^{2}}}+{ \ frac {\ částečný ^{2} u} {\ částečný z ^{2}}} = 0.}$

Zkoumáním Laplaceovy rovnice v sférických souřadnicích Thomson a Tait získali Laplaceovy sférické harmonické. (Viz část níže, „Harmonická polynomická reprezentace“.) Pojem „Laplaceovy koeficienty“ použil William Whewell k popisu konkrétního systému řešení zavedeného podle těchto linií, zatímco jiní si toto označení vyhradili pro zónové sférické harmonické, které byly řádně představili Laplace a Legendre.

Vývoj Fourierovy řady v 19. století umožnil řešení široké škály fyzikálních problémů v pravoúhlých oblastech, jako je řešení tepelné rovnice a vlnové rovnice . Toho lze dosáhnout rozšířením funkcí v sérii goniometrických funkcí . Zatímco goniometrické funkce ve Fourierově řadě představují základní režimy vibrací v řetězci , sférické harmonické představují základní režimy vibrací koule v podstatě stejným způsobem. Mnoho aspektů teorie Fourierovy řady by bylo možné zobecnit přijetím expanzí do sférických harmonických, nikoli do goniometrických funkcí. Kromě toho, analogicky k tomu, jak mohou být trigonometrické funkce ekvivalentně psány jako komplexní exponenciály , sférické harmonické také měly ekvivalentní formu jako komplexně hodnocené funkce. To bylo přínosem pro problémy s sférickou symetrií , jako jsou problémy s nebeskou mechanikou, které původně studovali Laplace a Legendre.

Prevalence sférických harmonických již ve fyzice připravila půdu pro jejich pozdější význam v zrodu kvantové mechaniky ve 20. století . (Složité) sférické harmonické jsou vlastní funkce druhé mocniny orbitálního operátoru hybnosti${\ Displaystyle S^{2} \ to \ mathbb {C}}$

${\ displaystyle -i \ hbar \ mathbf {r} \ times \ nabla,}$

a proto představují různé kvantované konfigurace atomových orbitálů .

Laplaceovy sférické harmonické

Laplaceova rovnice stanoví, že Laplacián skalárního pole f je nula. (Zde je skalární pole chápáno jako komplexní, tj. Odpovídá (hladké) funkci .) Ve sférických souřadnicích je toto: ${\ Displaystyle f: \ mathbb {R} ^{3} \ to \ mathbb {C}}$

${\ Displaystyle \ nabla^{2} f = {\ frac {1} {r^{2}}} {\ frac {\ partial} {\ partial r}} \ left (r^{2} {\ frac { \ částečné f} {\ částečné r}} \ vpravo)+{\ frac {1} {r^{2} \ sin \ theta}} {\ frac {\ částečné} {\ částečné \ theta}} \ vlevo (\ sin \ theta {\ frac {\ částečný f} {\ částečný \ theta}} \ vpravo)+{\ frac {1} {r ^{2} \ sin ^{2} \ theta}} {\ frac {\ částečný ^{2} f} {\ částečné \ varphi ^{2}}} = 0.}$

Zvažte problém hledání řešení ve tvaru f ( r , θ , φ ) = R ( r ) Y ( θ , φ ) . Tím, separace proměnných , dvě diferenciální rovnice způsobit tím, že ukládá Laplaceovy rovnice:

${\ Displaystyle {\ frac {1} {R}} {\ frac {d} {dr}} \ left (r^{2} {\ frac {dR} {dr}} \ right) = \ lambda, \ qquad {\ frac {1} {Y}} {\ frac {1} {\ sin \ theta}} {\ frac {\ částečný} {\ částečný \ theta}} \ vlevo (\ sin \ theta {\ frac {\ částečný Y} {\ částečná \ theta}} \ vpravo)+{\ frac {1} {Y}} {\ frac {1} {\ sin ^{2} \ theta}} {\ frac {\ částečná ^{2} Y} {\ částečné \ varphi ^{2}}} =-\ lambda.}$

Druhou rovnici lze zjednodušit za předpokladu, že Y má tvar Y ( θ , φ ) = Θ ( θ ) Φ ( φ ) . Opětovné použití separace proměnných na druhou rovnici ustoupí dvojici diferenciálních rovnic

${\ Displaystyle {\ frac {1} {\ Phi}} {\ frac {d^{2} \ Phi} {d \ varphi^{2}}} =-m^{2}}$

${\ Displaystyle \ lambda \ sin ^{2} \ theta +{\ frac {\ sin \ theta} {\ Theta}} {\ frac {d} {d \ theta}} \ left (\ sin \ theta {\ frac {d \ Theta} {d \ theta}} \ right) = m^{2}}$

pro nějaké číslo m . A priori, m je komplexní konstanta, ale protože Φ musí být periodická funkce, jejíž perioda rovnoměrně dělí 2 π , m je nutně celé číslo a Φ je lineární kombinace komplexních exponenciálů e ^{± imφ} . Funkce řešení Y ( θ , φ ) je pravidelná na pólech koule, kde θ = 0, π . Uložení této pravidelnosti do řešení Θ druhé rovnice v hraničních bodech domény je Sturm – Liouvilleův problém, který nutí parametr λ být ve tvaru λ = ℓ ( ℓ + 1) pro nějaké nezáporné celé číslo s ℓ ≥ | m | ; to je také vysvětleno níže z hlediska orbitálního momentu hybnosti . Navíc změna proměnných t = cos θ transformuje tuto rovnici na Legendrovu rovnici , jejíž řešení je násobkem přidruženého Legendrova polynomu P^m
_ℓ(cos θ ) . Nakonec má rovnice pro R řešení ve tvaru R ( r ) = A r ^ℓ + B r ^{- ℓ - 1} ; vyžadující řešení být pravidelné po celé R ³ síly B = 0 .

Zde se předpokládalo, že řešení má speciální tvar Y ( θ , φ ) = Θ ( θ ) Φ ( φ ) . Pro danou hodnotu ℓ existují 2 ℓ + 1 nezávislá řešení této formy, jedno pro každé celé číslo m s - ℓ ≤ m ≤ ℓ . Tato úhlová řešení jsou produktem goniometrických funkcí , zde reprezentovaných jako komplexní exponenciální , a souvisejících Legendrových polynomů: ${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$

${\ Displaystyle Y _ {\ ell}^{m} (\ theta, \ varphi) = Ne^{im \ varphi} P _ {\ ell}^{m} (\ cos {\ theta})}$

které splňují

${\ Displaystyle r^{2} \ nabla^{2} Y _ {\ ell}^{m} (\ theta, \ varphi) =-\ ell (\ ell +1) Y _ {\ ell}^{m} ( \ theta, \ varphi).}$

Zde se nazývá sférická harmonická funkce stupně ℓ a řádu m , je přidruženým Legendrovým polynomem , N je normalizační konstanta a θ a φ představují zeměpisnou délku a délku. Zejména colatitude θ nebo polární úhel se pohybuje od 0 na severním pólu, do π /2 na rovníku, do π na jižním pólu a zeměpisná délka φ nebo azimut může nabývat všech hodnot s 0 ≤ φ <2 π . Pro pevné celé číslo ℓ každé řešení Y ( θ , φ ) , problému vlastní hodnoty ${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$${\ Displaystyle P _ {\ ell}^{m}: [-1,1] \ to \ mathbb {R}}$ ${\ Displaystyle Y: S^{2} \ to \ mathbb {C}}$

${\ Displaystyle r ^{2} \ nabla ^{2} Y =-\ ell (\ ell +1) Y}$

je lineární kombinace z . Ve skutečnosti pro každé takové řešení r ^ℓ Y ( θ , φ ) je výraz v sférických souřadnicích homogenního polynomu, který je harmonický (viz níže ), a tak počítání dimenzí ukazuje, že existují 2 ℓ + 1 lineárně nezávislé takové polynomy . ${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$ ${\ Displaystyle \ mathbb {R} ^{3} \ to \ mathbb {C}}$

Obecné řešení na Laplaceova rovnice v kouli se středem v počátku je lineární kombinací sférických harmonických funkcí násobených vhodném měřítku faktor r ^pásmy , ${\ Displaystyle f: \ mathbb {R} ^{3} \ to \ mathbb {C}}$ ${\ displaystyle \ Delta f = 0}$

${\ Displaystyle f (r, \ theta, \ varphi) = \ sum _ {\ ell = 0}^{\ infty} \ sum _ {m =-\ ell}^{\ ell} f _ {\ ell}^{ m} r^{\ ell} Y _ {\ ell}^{m} (\ theta, \ varphi),}$

kde jsou konstanty a faktory r ^ℓ Y _ℓ ^m známé jako ( pravidelné ) pevné harmonické . Takové rozšíření platí v kouli${\ Displaystyle f _ {\ ell}^{m} \ in \ mathbb {C}}$ ${\ Displaystyle \ mathbb {R} ^{3} \ to \ mathbb {C}}$

${\ Displaystyle r <R = {\ frac {1} {\ limsup _ {\ ell \ to \ infty} | f _ {\ ell}^{m} |^{{1}/{\ ell}}}}. }$

Nebo místo toho jsou vybrány pevné harmonické se zápornými mocninami ( nepravidelné pevné harmonické ). V takovém případě je třeba rozšířit řešení známých oblastí v Laurentově řadě (o ), namísto výše uvedené Taylorovy řady (o ), aby odpovídalo výrazům a našlo koeficienty rozšiřování sérií . ${\ displaystyle r> R}$${\ displaystyle r}$ ${\ Displaystyle \ mathbb {R} ^{3} \ setminus \ {\ mathbf {0} \} \ to \ mathbb {C}}$${\ displaystyle r = \ infty}$${\ displaystyle r = 0}$${\ Displaystyle f _ {\ ell}^{m} \ in \ mathbb {C}}$

Oběžný moment hybnosti

V kvantové mechanice jsou Laplaceovy sférické harmonické chápány ve smyslu orbitálního momentu hybnosti

${\ Displaystyle \ mathbf {L} = -i \ hbar (\ mathbf {x} \ times \ mathbf {\ nabla}) = L_ {x} \ mathbf {i} +L_ {y} \ mathbf {j} +L_ {z} \ mathbf {k}.}$

Ħ je konvenční v kvantové mechanice; je vhodné pracovat v jednotkách, ve kterých ħ = 1 . Sférické harmonické jsou vlastní funkce druhé mocniny orbitálního momentu hybnosti

${\ Displaystyle {\ begin {aligned} \ mathbf {L} ^{2} & =-r ^{2} \ nabla ^{2}+\ left (r {\ frac {\ částečná} {\ částečná r}} +1 \ vpravo) r {\ frac {\ částečný} {\ částečný r}} \\ & =-{\ frac {1} {\ sin \ theta}} {\ frac {\ částečný} {\ částečný \ theta} } \ sin \ theta {\ frac {\ částečný} {\ částečný \ theta}}-{\ frac {1} {\ sin ^{2} \ theta}} {\ frac {\ částečný ^{2}} {\ částečné \ varphi ^{2}}}. \ end {aligned}}}$

Laplaceovy sférické harmonické jsou společné vlastní funkce čtverce orbitálního momentu hybnosti a generátoru otáček kolem azimutální osy:

${\ Displaystyle {\ begin {aligned} L_ {z} & =-i \ left (x {\ frac {\ částečná} {\ částečná y}}-y {\ frac {\ částečná} {\ částečná x}} \ vpravo) \\ & =-i {\ frac {\ částečný} {\ částečný \ varphi}}. \ end {zarovnaný}}}$

Tito operátoři dojíždějí a jsou hustě definovanými vlastními operátory na váženém Hilbertově prostoru funkcí f čtvercově integrovatelných s ohledem na normální rozdělení jako váhové funkce na R ³ :

${\ Displaystyle {\ frac {1} {(2 \ pi)^{3/2}}} \ int _ {\ mathbb {R}^{3}} | f (x) |^{2} e^{ -| x |^{2}/2} \, dx <\ infty.}$

Dále, L ² je pozitivní operátor .

Pokud Y je společná vlastní funkce L ² a L _z , pak podle definice

${\ displaystyle {\ begin {aligned} \ mathbf {L} ^{2} Y & = \ lambda Y \\ L_ {z} Y & = mY \ end {aligned}}}$

pro některá reálná čísla m a λ . Zde m musí být ve skutečnosti celé číslo, protože Y musí být periodické v souřadnici φ s periodou číslo, které rovnoměrně dělí 2 π . Navíc od

${\ Displaystyle \ mathbf {L}^{2} = L_ {x}^{2}+L_ {y}^{2}+L_ {z}^{2}}$

a každý z L _x , L _y , L _z jsou samostatně nastavitelné, z toho vyplývá, že λ ≥ m ² .

Označte tento společný vlastní prostor pomocí E _{λ , m} a definujte operátory zvedání a spouštění pomocí

${\ displaystyle {\ begin {aligned} L _ {+} & = L_ {x}+iL_ {y} \\ L _ {-} & = L_ {x} -iL_ {y} \ end {aligned}}}$

Pak L ₊ a L _- dojíždějí s L ² a Lieova algebra generovaná L ₊ , L _- , L _z je speciální lineární Lieova algebra řádu 2 , s komutačními vztahy ${\ displaystyle {\ mathfrak {sl}} _ {2} (\ mathbb {C})}$

${\ Displaystyle [L_ {z}, L _ {+}] = L _ {+}, \ quad [L_ {z}, L _ {-}] =-L _ {-}, \ quad [L _ {+}, L_ { -}] = 2L_ {z}.}$

Tedy L ₊  : E _{λ , m} → E _{λ , m +1} (je to „operátor zvedání“) a L _-  : E _{λ , m} → E _{λ , m −1} (je to „operátor spouštění“). Zejména L.^k
₊ : E _{λ , m} → E _{λ , m + k} musí být nulové pro k dostatečně velké, protože nerovnost λ  ≥  m ² musí platit v každém netriviálním kloubovém vlastním prostoru. Nechť Y  ∈  E _{λ , m} je nenulová společná vlastní funkce a k je nejmenší celé číslo, takže

${\ Displaystyle L _ {+}^{k} Y = 0.}$

Od té doby

${\ Displaystyle L _ {-} L _ {+} = \ mathbf {L} ^{2} -L_ {z} ^{2} -L_ {z}}$

z toho vyplývá, že

${\ Displaystyle 0 = L _ {-} L _ {+}^{k} Y = (\ lambda-(m+k)^{2}-(m+k)) Y.}$

Tedy λ = ℓ ( ℓ + 1) pro kladné celé číslo ℓ = m + k .

Výše uvedené bylo zpracováno v reprezentaci sférických souřadnic, ale může být vyjádřeno abstraktněji v úplném, ortonormálním sférickém ketovém základu . ${\ Displaystyle \ langle \ theta, \ phi | lm \ rangle = Y_ {l}^{m} (\ theta, \ phi)}$

Harmonická polynomická reprezentace

Sférické harmonické mohou být vyjádřeny jako omezení jednotkové sféry určitých polynomiálních funkcí . Konkrétně říkáme, že (komplexně hodnocená) polynomická funkce je homogenní stupně if ${\ Displaystyle \ mathbb {R} ^{3} \ to \ mathbb {C}}$${\ Displaystyle p: \ mathbb {R} ^{3} \ to \ mathbb {C}}$${\ displaystyle \ ell}$

${\ Displaystyle p (\ lambda \ mathbf {x}) = \ lambda ^{\ ell} p (\ mathbf {x})}$

pro všechna reálná čísla a pro všechny . Říkáme, že je to harmonické, pokud ${\ Displaystyle \ lambda \ in \ mathbb {R}}$${\ Displaystyle x \ in \ mathbb {R} ^{3}}$${\ displaystyle p}$

${\ displaystyle \ Delta p = 0,}$

kde je Laplacian ? Potom pro každého definujeme ${\ displaystyle \ Delta}$${\ displaystyle \ ell}$

${\ Displaystyle \ mathbf {A} _ {\ ell} = \ left \ {{\ text {harmonic polynomials}} \ mathbb {R} ^{3} \ to \ mathbb {C} {\ text {, které jsou homogenní stupeň}} \ ell \ right \}.}$

Například když , je pouze 3-dimenzionální prostor všech lineárních funkcí , protože každá taková funkce je automaticky harmonická. Mezitím, když máme 5-dimenzionální prostor: ${\ displaystyle \ ell = 1}$${\ displaystyle \ mathbf {A} _ {1}}$${\ Displaystyle \ mathbb {R} ^{3} \ to \ mathbb {C}}$${\ displaystyle \ ell = 2}$

${\ Displaystyle \ mathbf {A} _ {2} = \ operatorname {span} _ {\ mathbb {C}} (x_ {1} x_ {2}, \, x_ {1} x_ {3}, \, x_ {2} x_ {3}, \, x_ {1}^{2} -x_ {2}^{2}, \, x_ {1}^{2} -x_ {3}^{2}).}$

Pro všechny je prostor sférických harmonických stupňů pouze prostorem omezení sféry prvků . Jak bylo naznačeno v úvodu, tato perspektiva je pravděpodobně původem pojmu „sférická harmonická“ (tj. Omezení harmonické funkce na sféru ). ${\ displaystyle \ ell}$${\ displaystyle \ mathbf {H} _ {\ ell}}$${\ displaystyle \ ell}$${\ displaystyle S^{2}}$${\ displaystyle \ mathbf {A} _ {\ ell}}$

Například pro jakýkoli vzorec ${\ displaystyle c \ in \ mathbb {C}}$

${\ Displaystyle p (x_ {1}, x_ {2}, x_ {3}) = c (x_ {1}+ix_ {2})^{\ ell}}$

definuje homogenní polynom stupně s doménou a doménou , který je shodou okolností nezávislý na . Tento polynom je snadno viditelný jako harmonický. Pokud napíšeme sférické souřadnice a omezíme se na , získáme ${\ displaystyle \ ell}$${\ Displaystyle \ mathbb {R} ^{3} \ to \ mathbb {C}}$${\ displaystyle x_ {3}}$${\ displaystyle p}$${\ Displaystyle (r, \ theta, \ phi)}$${\ displaystyle r = 1}$

${\ Displaystyle p (\ theta, \ phi) = c \ sin (\ theta)^{\ ell} (\ cos (\ phi)+i \ sin (\ phi))^{\ ell},}$

které lze přepsat jako

${\ Displaystyle p (\ theta, \ phi) = c \ left ({\ sqrt {1- \ cos^{2} (\ theta)}} \ right)^{\ ell} e^{i \ ell \ phi }.}$

Po použití vzorce pro přidružený Legendreův polynom to můžeme rozpoznat jako vzorec pro sférickou harmonickou (Viz část níže o zvláštních případech sférických harmonických.) ${\ displaystyle P _ {\ ell}^{\ ell}}$${\ Displaystyle Y _ {\ ell}^{\ ell} (\ theta, \ phi).}$

Konvence

Ortogonalita a normalizace

Pro Laplaceovy sférické harmonické funkce se běžně používá několik různých normalizací . V celé sekci používáme standardní konvenci, která pro (viz související Legendreovy polynomy ) ${\ Displaystyle S^{2} \ to \ mathbb {C}}$${\ displaystyle m> 0}$

${\ Displaystyle P _ {\ ell}^{-m} = (-1)^{m} {\ frac {(\ ell -m)!} {(\ ell +m)!}} P _ {\ ell}^ {m}}$

což je přirozená normalizace daná Rodriguesovým vzorcem.

V akustice jsou Laplaceovy sférické harmonické obecně definovány jako (toto je konvence použitá v tomto článku)

${\ Displaystyle Y _ {\ ell}^{m} (\ theta, \ varphi) = {\ sqrt {{\ frac {(2 \ ell +1)} {4 \ pi}} {\ frac {(\ ell - m)!} {(\ ell +m)!}}}} \, P _ {\ ell}^{m} (\ cos {\ theta}) \, e^{im \ varphi}}$

zatímco v kvantové mechanice :

${\ Displaystyle Y _ {\ ell}^{m} (\ theta, \ varphi) = (-1)^{m} {\ sqrt {{\ frac {(2 \ ell +1)} {4 \ pi}} {\ frac {(\ ell -m)!} {(\ ell +m)!}}}} \, P _ {\ ell}^{m} (\ cos {\ theta}) \, e^{im \ varphi}}$

kde jsou přidružené Legendrovy polynomy bez fáze Condon – Shortley (aby se zabránilo započítávání fáze dvakrát). ${\ displaystyle P _ {\ ell}^{m}}$

V obou definicích jsou sférické harmonické ortonormální

${\ Displaystyle \ int _ {\ theta = 0}^{\ pi} \ int _ {\ varphi = 0}^{2 \ pi} Y _ {\ ell}^{m} \, Y _ {\ ell '}^ {m '} {}^{*} \, d \ Omega = \ delta _ {\ ell \ ell'} \, \ delta _ {mm '},}$

kde delta _ij je Kroneckerovo delta a d Ω = sin ( θ ) dφ dθ . Tato normalizace se používá v kvantové mechanice, protože zajišťuje, že pravděpodobnost je normalizována, tzn

${\ Displaystyle \ int {| Y _ {\ ell}^{m} |^{2} d \ Omega} = 1.}$

Disciplíny geodézie a spektrální analýzy

${\ Displaystyle Y _ {\ ell}^{m} (\ theta, \ varphi) = {\ sqrt {{(2 \ ell +1)} {\ frac {(\ ell -m)!} {(\ ell + m)!}}}} \, P _ {\ ell}^{m} (\ cos {\ theta}) \, e^{im \ varphi}}$

které mají jednotkovou sílu

${\ Displaystyle {\ frac {1} {4 \ pi}} \ int _ {\ theta = 0}^{\ pi} \ int _ {\ varphi = 0}^{2 \ pi} Y _ {\ ell}^ {m} \, Y _ {\ ell '}^{m'} {}^{*} d \ Omega = \ delta _ {\ ell \ ell '} \, \ delta _ {mm'}.}$

Magnetismu komunita je naproti tomu využívá Schmidt semi-normalizované harmonických

${\ Displaystyle Y _ {\ ell}^{m} (\ theta, \ varphi) = {\ sqrt {\ frac {(\ ell -m)!} {(\ ell +m)}}} \, P_ { \ ell}^{m} (\ cos {\ theta}) \, e^{im \ varphi}}$

které mají normalizaci

${\ Displaystyle \ int _ {\ theta = 0}^{\ pi} \ int _ {\ varphi = 0}^{2 \ pi} Y _ {\ ell}^{m} \, Y _ {\ ell '}^ {m '} {}^{*} d \ Omega = {\ frac {4 \ pi} {(2 \ ell +1)}} \ delta _ {\ ell \ ell'} \, \ delta _ {mm ' }.}$

V kvantové mechanice se někdy používá i tato normalizace a je pojmenována Racahova normalizace podle Giulia Racaha .

Lze ukázat, že všechny výše uvedené normalizované sférické harmonické funkce splňují

${\ Displaystyle Y _ {\ ell}^{m} {}^{*} (\ theta, \ varphi) = (-1)^{m} Y _ {\ ell}^{-m} (\ theta, \ varphi ),}$

kde horní index * označuje komplexní konjugaci. Alternativně tato rovnice vyplývá ze vztahu sférických harmonických funkcí s Wignerovou D-maticí .

Fáze Condon – Shortley

Jeden zdroj záměny s definicí sférických harmonických funkcí se týká fázového faktoru (−1) ^m , který se v kvantově mechanické literatuře běžně označuje jako fáze Condon – Shortley. V komunitě kvantové mechaniky je běžnou praxí buď zahrnout tento fázový faktor do definice přidružených Legendrových polynomů , nebo jej připojit k definici sférických harmonických funkcí. Neexistuje žádný požadavek na použití fáze Condon – Shortley při definování sférických harmonických funkcí, ale její zahrnutí může zjednodušit některé kvantově mechanické operace, zejména aplikaci zvedání a spouštění operátorů . Geodetická a magnetická společenství nikdy neobsahují fázový faktor Condon – Shortley ve svých definicích sférických harmonických funkcí ani v přidružených Legendrových polynomech.

Skutečná forma

Skutečný základ sférických harmonických lze definovat z hlediska jejich komplexních analogů nastavením ${\ Displaystyle Y _ {\ ell m}: S^{2} \ to \ mathbb {R}}$${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$

Pro konzistenci se zde používá konvenční fáze Condon – Shortley. Odpovídající inverzní rovnice definující komplexní sférické harmonické z hlediska skutečných sférických harmonických jsou ${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$${\ Displaystyle Y _ {\ ell m}: S^{2} \ to \ mathbb {R}}$

Skutečné sférické harmonické jsou někdy známé jako tesserální sférické harmonické . Tyto funkce mají stejné vlastnosti orthonormality jako výše uvedené komplexní . Skutečné sférické harmonické s m  > 0 jsou kosinového typu a ty s m  <0 sinusového typu. Důvod je vidět v zápisu funkcí z hlediska Legendrových polynomů jako ${\ Displaystyle Y _ {\ ell m}: S^{2} \ to \ mathbb {R}}$${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$${\ displaystyle Y _ {\ ell m}}$

Stejné sinusové a kosinové faktory lze také vidět v následující podsekci, která se zabývá karteziánskou reprezentací.

Viz zde pro seznam skutečných sférických až do a včetně , které mohou být viděny, aby byly konzistentní s výkonem výše uvedených rovnic. ${\ displaystyle \ ell = 4}$

Použití v kvantové chemii

Jak je známo z analytických řešení pro atom vodíku, vlastní funkce úhlové části vlnové funkce jsou sférické harmonické. Řešení nerelativistické Schrödingerovy rovnice bez magnetických členů je však možné uskutečnit. To je důvod, proč jsou skutečné formy široce používány v základních funkcích pro kvantovou chemii, protože programy pak nepotřebují používat komplexní algebru. Zde je důležité si uvědomit, že skutečné funkce pokrývají stejný prostor jako komplexní funkce.

Například, jak je vidět z tabulky sférických harmonických , obvyklé funkce p ( ) jsou složité a mísí směry os, ale skutečné verze jsou v podstatě jen x , y a z . ${\ displaystyle \ ell = 1}$

Sférické harmonické v karteziánské formě

Složité sférické harmonické dávají vzniknout plným harmonickým tím, že se rozšiřují na všechny jako homogenní funkce stupně , tj. Nastavení ${\ displaystyle Y _ {\ ell}^{m}}$${\ displaystyle S^{2}}$${\ displaystyle \ mathbb {R} ^{3}}$${\ displaystyle \ ell}$

${\ Displaystyle R _ {\ ell}^{m} (v): = \ | v \ |^{\ ell} Y _ {\ ell}^{m} ({\ frac {v} {\ | v \ |} })}$

Ukázalo se, že je základem prostoru harmonických a homogenních polynomů stupně . Přesněji řečeno, je to (jedinečný až normalizační) Gelfand-Tsetlinův základ této reprezentace rotační skupiny a z této skutečnosti lze odvodit explicitní vzorec pro v kartézských souřadnicích. ${\ displaystyle R _ {\ ell}^{m}}$${\ displaystyle \ ell}$${\ displaystyle SO (3)}$${\ displaystyle R _ {\ ell}^{m}}$

Funkce generující Herglotz

Pokud je přijata kvantově mechanická konvence pro , pak ${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$

${\ Displaystyle e^{v {\ mathbf {a}} \ cdot {\ mathbf {r}}} = \ sum _ {\ ell = 0}^{\ infty} \ sum _ {m =-\ ell}^ {\ ell} {\ sqrt {\ frac {4 \ pi} {2 \ ell +1}}} {\ frac {r^{\ ell} v^{\ ell} {\ lambda^{m}}} { \ sqrt {(\ ell +m)! (\ ell -m)!}}} Y _ {\ ell}^{m} (\ mathbf {r} /r).}$

Tady, je vektor s komponentami , a ${\ displaystyle \ mathbf {r}}$${\ Displaystyle (x, y, z) \ in \ mathbb {R} ^{3}}$${\ displaystyle r = | \ mathbf {r} |}$

${\ Displaystyle {\ mathbf {a}} = {\ mathbf {\ hat {z}}}-{\ frac {\ lambda} {2}} \ left ({\ mathbf {\ hat {x}}}+i {\ mathbf {\ hat {y}}} \ right)+{\ frac {1} {2 \ lambda}} \ left ({\ mathbf {\ hat {x}}} -i {\ mathbf {\ hat { y}}} \ right)}$

je vektor s komplexními koeficienty. Stačí vzít a jako skutečné parametry. Základní vlastností je, že je null: ${\ displaystyle v}$${\ Displaystyle \ lambda}$${\ displaystyle \ mathbf {a}}$

${\ Displaystyle \ mathbf {a} \ cdot \ mathbf {a} = 0.}$

Při pojmenování této generující funkce po Herglotzovi se řídíme Courant & Hilbert 1962 , §VII.7, který za jeho objev připisuje jím dosud nepublikované poznámky.

Z této generující funkce lze v podstatě odvodit všechny vlastnosti sférických harmonických. Bezprostřední výhoda této definice je to, že v případě, že vektor je nahrazen operátorem quantum mechanická rotace vektoru tak, že je provozovatelem analog pevné harmonické , se získá v závislosti generující pro standardizovaný soubor sférických operátorů tensor , : ${\ displaystyle \ mathbf {r}}$${\ displaystyle \ mathbf {J}}$${\ displaystyle {\ mathcal {Y}} _ {\ ell}^{m} ({\ mathbf {J}})}$ ${\ Displaystyle r^{\ ell} Y _ {\ ell}^{m} (\ mathbf {r} /r)}$${\ displaystyle {\ mathcal {Y}} _ {\ ell}^{m} ({\ mathbf {J}})}$

${\ Displaystyle e^{v {\ mathbf {a}} \ cdot {\ mathbf {J}}} = \ sum _ {\ ell = 0}^{\ infty} \ sum _ {m =-\ ell}^ {\ ell} {\ sqrt {\ frac {4 \ pi} {2 \ ell +1}}} {\ frac {v ^{\ ell} {\ lambda ^{m}}} {\ sqrt {(\ ell +m)! (\ ell -m)!}}} {\ mathcal {Y}} _ {\ ell}^{m} ({\ mathbf {J}}).}$

Rovnoběžnost dvě definice zajišťuje, že ‚je transformovat za rotace (viz níže), stejně jako ‘ s, což ve svém důsledku zaručuje, že jsou kulové tenzorové operátory, s a , se řídit všechny vlastnosti těchto subjektů, jako je věta o kompozici Clebsch-Gordan a Wigner-Eckartova věta . Jsou to navíc standardizovaná sada s pevným měřítkem nebo normalizací. ${\ displaystyle {\ mathcal {Y}} _ {\ ell}^{m}}$${\ displaystyle Y _ {\ ell}^{m}}$${\ displaystyle T_ {q}^{(k)}}$${\ displaystyle k = {\ ell}}$${\ Displaystyle q = m}$

Oddělená karteziánská forma

Herglotzianova definice poskytuje polynomy, které lze, pokud si to někdo přeje, dále rozložit na polynom a další a následovně (fáze Condon – Shortley): ${\ Displaystyle z}$${\ displaystyle x}$${\ displaystyle y}$

${\ Displaystyle r^{\ ell} \, {\ begin {pmatrix} Y _ {\ ell}^{m} \\ Y _ {\ ell}^{-m} \ end {pmatrix}} = \ left [{\ frac {2 \ ell +1} {4 \ pi}} \ right]^{1/2} {\ bar {\ Pi}} _ {\ ell}^{m} (z) {\ begin {pmatrix} \ vlevo (-1 \ vpravo)^{m} (A_ {m}+iB_ {m}) \\ (A_ {m} -iB_ {m}) \ end {pmatrix}}, \ qquad m> 0.}$

a pro m = 0:

${\ Displaystyle r^{\ ell} \, Y _ {\ ell}^{0} \ equiv {\ sqrt {\ frac {2 \ ell +1} {4 \ pi}}} {\ bar {\ Pi}} _ {\ ell}^{0}.}$

Tady

${\ Displaystyle A_ {m} (x, y) = \ sum _ {p = 0}^{m} {\ binom {m} {p}} x^{p} y^{mp} \ cos \ left ( (mp) {\ frac {\ pi} {2}} \ vpravo),}$

${\ Displaystyle B_ {m} (x, y) = \ sum _ {p = 0}^{m} {\ binom {m} {p}} x^{p} y^{mp} \ sin \ left ( (mp) {\ frac {\ pi} {2}} \ vpravo),}$

a

${\ Displaystyle {\ bar {\ Pi}} _ {\ ell}^{m} (z) = \ left [{\ frac {(\ ell -m)!} {(\ ell +m)!}} \ vpravo]^{1/2} \ součet _ {k = 0}^{\ left \ lfloor (\ ell -m)/2 \ right \ rfloor} (-1)^{k} 2^{-\ ell} {\ binom {\ ell} {k}} {\ binom {2 \ ell -2k} {\ ell}} {\ frac {(\ ell -2k)!} {(\ ell -2k -m)!}} \; r^{2k} \; z^{\ ell -2k -m}.}$

Pro toto sesadí na ${\ displaystyle m = 0}$

${\ Displaystyle {\ bar {\ Pi}} _ {\ ell}^{0} (z) = \ sum _ {k = 0}^{\ left \ lfloor \ ell /2 \ right \ rfloor} (-1 )^{k} 2^{ -\ ell} {\ binom {\ ell} {k}} {\ binom {2 \ ell -2k} {\ ell}} \; r^{2k} \; z^{ \ ell -2k}.}$

Faktor je v podstatě přidružený Legendreův polynom a faktory jsou v podstatě . ${\ displaystyle {\ bar {\ Pi}} _ {\ ell}^{m} (z)}$${\ Displaystyle P _ {\ ell}^{m} (\ cos \ theta)}$${\ Displaystyle (A_ {m} \ pm iB_ {m})}$${\ Displaystyle e^{\ pm im \ varphi}}$

Příklady

Pomocí výrazů pro , a uvedených výše výslovně získáme: ${\ displaystyle {\ bar {\ Pi}} _ {\ ell}^{m} (z)}$${\ displaystyle A_ {m} (x, y)}$${\ displaystyle B_ {m} (x, y)}$

${\ Displaystyle Y_ {3}^{1} =-{\ frac {1} {r^{3}}} \ left [{\ tfrac {7} {4 \ pi}} \ cdot {\ tfrac {3} {16}} \ right]^{1/2} \ left (5z^{2} -r^{2} \ right) \ left (x+iy \ right) =-\ left [{\ tfrac {7} {4 \ pi}} \ cdot {\ tfrac {3} {16}} \ right] ^{1/2} \ left (5 \ cos ^{2} \ theta -1 \ right) \ left (\ sin \ theta e^{i \ varphi} \ right)}$

${\ Displaystyle Y_ {4}^{-2} = {\ frac {1} {r^{4}}} \ left [{\ tfrac {9} {4 \ pi}} \ cdot {\ tfrac {5} {32}} \ right]^{1/2} \ left (7z^{2} -r^{2} \ right) \ left (x-iy \ right)^{2} = \ left [{\ tfrac {9} {4 \ pi}} \ cdot {\ tfrac {5} {32}} \ right] ^{1/2} \ left (7 \ cos ^{2} \ theta -1 \ right) \ left ( \ sin ^{2} \ theta e ^{-2i \ varphi} \ right)}$

Lze ověřit, že to souhlasí s funkcí uvedenou zde a zde .

Skutečné formy

Pomocí výše uvedených rovnic k vytvoření skutečných sférických harmonických je vidět, že jsou zahrnuty pouze termíny (kosiny) a pouze termíny (sinusy): ${\ displaystyle m> 0}$${\ displaystyle A_ {m}}$${\ Displaystyle m <0}$${\ displaystyle B_ {m}}$

${\ Displaystyle r^{\ ell} \, {\ begin {pmatrix} Y _ {\ ell m} \\ Y _ {\ ell -m} \ end {pmatrix}} = {\ sqrt {\ frac {2 \ ell + 1} {2 \ pi}}} {\ bar {\ Pi}} _ {\ ell}^{m} (z) {\ begin {pmatrix} A_ {m} \\ B_ {m} \ end {pmatrix} }, \ qquad m> 0.}$

a pro m = 0:

${\ Displaystyle r^{\ ell} \, Y _ {\ ell 0} \ equiv {\ sqrt {\ frac {2 \ ell +1} {4 \ pi}}} {\ bar {\ Pi}} _ {\ vše}^{0}.}$

Zvláštní případy a hodnoty

1. Když se sférické harmonické redukují na běžné Legendreovy polynomy :${\ displaystyle m = 0}$${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$
   $${\ Displaystyle Y _ {\ ell}^{0} (\ theta, \ varphi) = {\ sqrt {\ frac {2 \ ell +1} {4 \ pi}}} P _ {\ ell} (\ cos \ theta ).}$$

   
2. Když ,${\ Displaystyle m = \ pm \ ell}$
   $${\ Displaystyle Y _ {\ ell}^{\ pm \ ell} (\ theta, \ varphi) = {\ frac {(\ mp 1)^{\ ell}} {2^{\ ell} \ ell!}} {\ sqrt {\ frac {(2 \ ell +1)!} {4 \ pi}}} \ sin ^{\ ell} \ theta \, e ^{\ pm i \ ell \ varphi},}$$

   
   nebo jednoduše v kartézských souřadnicích,
   $${\ Displaystyle r^{\ ell} Y _ {\ ell}^{\ pm \ ell} ({\ mathbf {r}}) = {\ frac {(\ mp 1)^{\ ell}} {2^{ \ ell} \ ell!}} {\ sqrt {\ frac {(2 \ ell +1)!} {4 \ pi}}} (x \ pm iy)^{\ ell}.}$$

   
3. Na severním pólu, kde a není definováno, všechny sférické harmonické kromě těch, které zmizí:${\ displaystyle \ theta = 0}$${\ Displaystyle \ varphi}$${\ displaystyle m = 0}$
   $${\ Displaystyle Y _ {\ ell}^{m} (0, \ varphi) = Y _ {\ ell}^{m} ({\ mathbf {z}}) = {\ sqrt {\ frac {2 \ ell +1 } {4 \ pi}}} \ delta _ {m0}.}$$

   

Vlastnosti symetrie

Sférické harmonické mají hluboké a následné vlastnosti při operacích prostorové inverze (parity) a rotace.

Parita

Sférické harmonické mají určitou paritu. To znamená, že jsou buď sudé nebo liché, pokud jde o inverzi o původu. Inverzi zastupuje operátor . Potom, jak je vidět v mnoha ohledech (možná nejjednodušeji z generující funkce Herglotz), s tím, že je jednotkovým vektorem, ${\ Displaystyle P \ Psi (\ mathbf {r}) = \ Psi (-\ mathbf {r})}$${\ displaystyle \ mathbf {r}}$

${\ Displaystyle Y _ {\ ell}^{m} (-\ mathbf {r}) = (-1)^{\ ell} Y _ {\ ell}^{m} (\ mathbf {r}).}$

Pokud jde o sférické úhly, parita transformuje bod se souřadnicemi na . Vyjádření parity sférických harmonických je pak ${\ displaystyle \ {\ theta, \ phi \}}$${\ Displaystyle \ {\ pi -\ theta, \ pi +\ phi \}}$

${\ Displaystyle Y _ {\ ell}^{m} (\ theta, \ phi) \ rightarrow Y _ {\ ell}^{m} (\ pi -\ theta, \ pi +\ phi) = ( -1)^{ \ ell} Y _ {\ ell}^{m} (\ theta, \ phi)}$

(Lze to vidět následovně: Přidružené Legendrovy polynomy dávají (−1) ^{ℓ + m} a z exponenciální funkce máme (−1) ^m , což dává dohromady pro sférické harmonické paritu (−1) ^ℓ .)

Parita nadále platí pro skutečné sférické harmonické a pro sférické harmonické ve vyšších dimenzích: použití bodového odrazu na sférickou harmonickou stupně ℓ mění znaménko faktorem (−1) ^ℓ .

Rotace

Vezměme si rotaci o původu, který vysílá jednotkový vektor se . Při této operaci se sférická harmonická stupně a řádu transformuje na lineární kombinaci sférických harmonických stejného stupně. To znamená, ${\ displaystyle {\ mathcal {R}}}$${\ displaystyle \ mathbf {r}}$${\ displaystyle \ mathbf {r} '}$${\ displaystyle \ ell}$${\ displaystyle m}$

${\ Displaystyle Y _ {\ ell}^{m} ({\ mathbf {r}} ') = \ sum _ {m' =-\ ell}^{\ ell} A_ {mm '} Y _ {\ ell}^ {m '} ({\ mathbf {r}}),}$

kde je matice řádu, která závisí na rotaci . Toto však není standardní způsob vyjádření této vlastnosti. Standardním způsobem se píše: ${\ displaystyle A_ {mm '}}$${\ displaystyle (2 \ ell +1)}$${\ displaystyle {\ mathcal {R}}}$

${\ Displaystyle Y _ {\ ell}^{m} ({\ mathbf {r}} ') = \ sum _ {m' =-\ ell}^{\ ell} [D_ {mm '}^{(\ ell )} ({\ mathcal {R}})]^{*} Y _ {\ ell}^{m '} ({\ mathbf {r}}),}$

kde je komplexní konjugát prvku Wignerovy D-matice . Zejména když je rotace azimutu, získáme identitu, ${\ Displaystyle D_ {mm '}^{(\ ell)} ({\ mathcal {R}})^{*}}$${\ displaystyle \ mathbf {r} '}$${\ displaystyle \ phi _ {0}}$

${\ Displaystyle Y _ {\ ell}^{m} ({\ mathbf {r}} ') = Y _ {\ ell}^{m} ({\ mathbf {r}}) e^{im \ phi _ {0 }}.}$

Rotační chování sférických harmonických je možná jejich typickým rysem z hlediska teorie skupin. K ‚s ve stupni poskytují základní sadu funkcí pro ireducibilní zobrazení skupiny SO (3) rozměru . Mnoho faktů o sférických harmonických (jako je adiční věta), které jsou pracně prokázány pomocí analytických metod, získává jednodušší důkazy a hlubší význam pomocí metod symetrie. ${\ displaystyle Y _ {\ ell}^{m}}$${\ displaystyle \ ell}$${\ displaystyle (2 \ ell +1)}$

Rozšíření sférických harmonických

Laplaceova sférických tvoří kompletní sadu ortonormální funkcí, a tím tvoří ortonormální báze o Hilbertova prostoru ze čtvercového integrovatelných funkcí . Na jednotkové sféře lze tedy jakoukoli funkci integrovatelnou do čtverce rozšířit jako lineární kombinaci těchto: ${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$ ${\ displaystyle L _ {\ mathbb {C}}^{2} (S^{2})}$${\ displaystyle S^{2}}$${\ Displaystyle f: S^{2} \ to \ mathbb {C}}$

${\ Displaystyle f (\ theta, \ varphi) = \ sum _ {\ ell = 0}^{\ infty} \ sum _ {m =-\ ell}^{\ ell} f _ {\ ell}^{m} \, Y _ {\ ell}^{m} (\ theta, \ varphi).}$

Tato expanze platí ve smyslu konvergence průměr-čtverec-konvergence v L ² sféry-což znamená, že

${\ Displaystyle \ lim _ {N \ to \ infty} \ int _ {0}^{2 \ pi} \ int _ {0}^{\ pi} \ left | f (\ theta, \ varphi)-\ sum _ {\ ell = 0}^{N} \ sum _ {m =-\ ell}^{\ ell} f _ {\ ell}^{m} Y _ {\ ell}^{m} (\ theta, \ varphi ) \ right |^{2} \ sin \ theta \, d \ theta \, d \ varphi = 0.}$

Expanzní koeficienty jsou analogiemi Fourierových koeficientů a lze je získat vynásobením výše uvedené rovnice komplexním konjugátem sférické harmonické, integrací přes pevný úhel Ω a využitím výše uvedených vztahů ortogonality. To je přísně odůvodněno základní Hilbertovou vesmírnou teorií. V případě ortonormalizovaných harmonických to dává:

${\ Displaystyle f _ {\ ell}^{m} = \ int _ {\ Omega} f (\ theta, \ varphi) \, Y _ {\ ell}^{m*} (\ theta, \ varphi) \, d \ Omega = \ int _ {0}^{2 \ pi} d \ varphi \ int _ {0}^{\ pi} \, d \ theta \, \ sin \ theta f (\ theta, \ varphi) Y_ { \ ell}^{m*} (\ theta, \ varphi).}$

V případě, že koeficienty rozpadne pásmy dostatečně rychle, - například exponenciálně - pak řada také konverguje stejnoměrně k f .

Funkce integrovatelná do čtverců může být také rozšířena o součet skutečných harmonických výše ${\ Displaystyle f: S^{2} \ to \ mathbb {R}}$${\ Displaystyle Y _ {\ ell m}: S^{2} \ to \ mathbb {R}}$

${\ Displaystyle f (\ theta, \ varphi) = \ sum _ {\ ell = 0}^{\ infty} \ sum _ {m =-\ ell}^{\ ell} f _ {\ ell m} \, Y_ {\ ell m} (\ theta, \ varphi).}$

Konvergence série platí opět ve stejném smyslu, a to skutečné sférických tvoří kompletní sadu ortonormální funkcí, a tím tvoří ortonormální báze o Hilbertova prostoru ze čtvercového integrovatelných funkcí . Výhodou expanze z hlediska skutečných harmonických funkcí je, že u reálných funkcí jsou koeficienty expanze zaručeny jako skutečné, zatímco jejich koeficienty v expanzi, pokud jde o (považujíce je za funkce ), tuto vlastnost nemají. ${\ Displaystyle Y _ {\ ell m}: S^{2} \ to \ mathbb {R}}$ ${\ Displaystyle L _ {\ mathbb {R}}^{2} (S^{2})}$${\ displaystyle Y _ {\ ell m}}$${\ Displaystyle f: S^{2} \ to \ mathbb {R}}$${\ displaystyle f _ {\ ell m}}$${\ displaystyle f _ {\ ell}^{m}}$${\ displaystyle Y _ {\ ell}^{m}}$${\ Displaystyle f: S^{2} \ to \ mathbb {C} \ supset \ mathbb {R}}$

Harmonické tenzory

Vzorec

Harmonické funkce jsou v teoretické fyzice zpravidla užitečné při zvažování polí ve vzdáleném poli, když je vzdálenost od nábojů mnohem větší než velikost jejich umístění. V tomto případě je poloměr R konstantní a souřadnice ( θ , φ ) lze pohodlně použít. Teoretická fyzika zvažuje mnoho problémů, když je potřeba řešení Laplaceovy rovnice jako funkce Сartesian souřadnic. Současně je důležité získat invariantní formu řešení vzhledem k rotaci prostoru nebo, obecně řečeno, vůči skupinovým transformacím. Nejjednodušší tenzorová řešení - dipólové, kvadrupólové a oktupolové potenciály - jsou základními pojmy obecné fyziky:

${\ displaystyle {\ begin {aligned} T_ {i}^{(1)} = x_ {i}, \\ T_ {ik}^{(2)} = 3x {_ {i}} x {_ {k }}-\ delta _ {ik} r^{2}, \\ T_ {ikn}^{(3)} = 15x {_ {i}} x {_ {k}} x {_ {n}}- 3 \ delta _ {ik} {r^{2}} x {_ {n}}-3 \ delta _ {kn} {r^{2}} x {_ {i}}-3 \ delta _ {ni } {r^{2}} x {_ {k}}. \ end {aligned}}}$

Je snadné ověřit, že jde o harmonické funkce. Celková sada tenzorů je definována Taylorovou řadou potenciálu pole bodového náboje pro : ${\ displaystyle r_ {0} <r}$

${\ displaystyle {\ frac {1} {\ left | {\ boldsymbol {rr}} {_ {0}} \ right |}} = \ sum _ {l} (-1)^{l} {\ frac { {({\ boldsymbol {r_ {0}}} \ nabla)}^{l}} {l!}} {\ frac {1} {r}} = \ sum _ {l} {\ frac {x_ {0i } \ ldots x_ {0k}} {l! \, r^{2l+1}}} T_ {i \ ldots k}^{(l)} ({\ boldsymbol {r}}) = \ sum _ {l } {\ frac {\ left [\ otimes {\ boldsymbol {{r_ {0}}^{l} T^{(l)}}} \ right]} {l! \, r^{2l+1}} },}$

kde tenzor je označen symbolem a smrštění tenzorů je v závorkách [...]. Proto je tenzor definován -tou derivací tenzoru: ${\ displaystyle x_ {0i} \ ldots x_ {0k}}$${\ Displaystyle \ otimes {\ boldsymbol {r_ {0}}}^{l}}$${\ displaystyle {\ boldsymbol {T}}^{(l)}}$${\ Displaystyle l}$

${\ displaystyle {\ frac {\ boldsymbol {T^{(l)}}} {r^{(2l+1)}}}} = (-\ otimes {\ boldsymbol {\ nabla}})^{l} { \ frac {1} {r}}}$

James Clerk Maxwell přirozeně použil podobné úvahy bez tenzorů. EW Hobson analyzoval také Maxwellovu metodu. Z rovnice lze vidět následující vlastnosti, které se opakují hlavně u pevných a sférických funkcí.

• Tenzor je harmonický polynom, tj .${\ displaystyle \ Delta {\ boldsymbol {T}}^{(l)} = 0}$
• Trasování přes každý pár indexů je nulové .${\ textstyle \ Delta {\ frac {1} {r}} = 0}$
• Tenzor je homogenní polynom stupně, tj. Součet stupňů proměnných x, y, z každé položky je roven .${\ Displaystyle l}$${\ Displaystyle l}$
• Tenzor má invariantní formu při otáčení proměnných x, y, z tj. Vektoru .${\ displaystyle \ mathbf {r}}$
• Celková sada potenciálů je kompletní.${\ displaystyle \ mathbf {T} ^{(l)}}$
• Kontrakce tenzoru je úměrná kontrakci dvou harmonických potenciálů:${\ displaystyle \ mathbf {T} ^{(l)} (\ mathbf {r})}$${\ Displaystyle \ otimes {\ boldsymbol {\ rho}}^{l}}$
  $${\ Displaystyle \ left [\ mathbf {T} ^{(l)} (\ mathbf {r}) \ otimes {\ boldsymbol {\ rho}} ^{l} \ right] = {\ frac {1} {( 2l-1) !!}} \ left [\ mathbf {T} ^{(l)} (\ mathbf {r}) \ mathbf {T} ^{(l)} ({\ boldsymbol {\ rho}}) \že jo]}$$

  

Vzorec pro harmonický invariantní tenzor byl nalezen v papíru. Podrobný popis je uveden v monografii. 4-D harmonické tenzory jsou důležité ve Fockově symetrii nalezené v kvantově Coulombově problému. Vzorec obsahuje produkty tenzorů a Kroneckerových symbolů : ${\ Displaystyle x_ {i} \ ldots x_ {k} = \ mathbf {\ otimes} r^{m}}$ ${\ displaystyle \ delta _ {ik}}$

${\ Displaystyle \ mathbf {T}^{(l)} = (2l-1) !! \ \ mathbf {(} \ otimes r^{l})-(2l-3) !! \ r^{2} \ left \ langle \ otimes \ mathbf {r} ^{(l-2)} \ otimes {\ mathsf {\ boldsymbol {\ delta}}} ^{1} \ right \ rangle +(2l-5) !! \ r^{4} \ left \ langle \ otimes \ mathbf {r}^{(l -4)} \ otimes {\ mathsf {\ boldsymbol {\ delta}}}^{2} \ right \ rangle -\ cdots}$

Když se rozsah tenzorů odpovídajícím způsobem sníží o dva, počet symbolů Kroneckera se zvýší o dva v součinu každé následující položky . Operace symetrizuje tenzor pomocí sečtení všech nezávislých permutací indexů. Zejména není třeba každý transformovat a tenzory se nestávají . ${\ displaystyle x_ {i} \ tečky x_ {k}}$${\ Displaystyle \ left \ langle \ cdot \ right \ rangle}$${\ displaystyle \ delta _ {ik}}$${\ displaystyle \ delta _ {ki}}$${\ displaystyle x_ {i} x_ {k}}$${\ displaystyle x_ {k} x_ {i}}$

Tyto tenzory je vhodné nahradit do Laplaceovy rovnice:

${\ Displaystyle \ Delta \ left \ langle \ otimes \ mathbf {r} ^{(l-2k)} \ otimes {\ mathsf {\ boldsymbol {\ delta}}} ^{k} \ right \ rangle = 2 \ left \ langle \ otimes \ mathbf {r} ^{(l-2k-2)} \ otimes {\ mathsf {\ boldsymbol {\ delta}}} ^{(k+2)} \ right \ rangle, \ quad (\ mathbf {r} \ mathbf {\ nabla}) \ left \ langle \ otimes \ mathbf {r} ^{(l-2k)} \ otimes {\ mathsf {\ boldsymbol {\ delta}}}} ^{(k)} \ right \ rangle = l \ left \ langle \ otimes \ mathbf {r} ^{(l-2k)} \ otimes {\ mathsf {\ boldsymbol {\ delta}}} ^{(k)} \ right \ rangle. }$

Poslední relací je Eulerův vzorec pro homogenní polynomy . Laplaceův operátor nemá vliv na souměrnost indexu tenzorů. Tyto dva vztahy umožňují substituci tenzoru do Laplaceovy rovnice a přímo ověřit, zda je tenzor harmonickou funkcí: ${\ displaystyle \ Delta}$

${\ Displaystyle \ Delta \ mathbf {T} ^{(l)} = 0.}$

Zjednodušené momenty

Poslední vlastnost je pro teoretickou fyziku důležitá z následujícího důvodu. Potenciál nábojů mimo jejich umístění je integrální, aby se rovnal součtu vícepólových potenciálů:

${\ Displaystyle \ iiint {\ frac {f ({\ boldsymbol {r}})} {\ left || \ mathbf {rr} {_ {0}} \ right |}} \, dx \, dy \, dz = \ sum _ {l} \ iiint f (\ mathbf {r}) \ left [\ mathbf {T} ^{(l)} (\ mathbf {r}) dx \, dy \, dz {\ frac {\ mathbf {T} ^{(l)} (\ mathbf {r} _ {0})} {(2l-1) !! \, l! \, r_ {0} ^{(2l+1)}}}} \že jo],}$

kde je hustota náboje. Konvoluce se přirozeně aplikuje na tenzory ve vzorci. Integrály v součtu se ve fyzice nazývají vícepólové momenty . Tři z nich se používají aktivně, zatímco jiné se používají méně často, protože jejich struktura (nebo struktura sférických funkcí) je složitější. Poslední vlastnost však dává cestu ke zjednodušení výpočtů v teoretické fyzice použitím integrálů s tenzorem místo harmonického tenzoru . Zjednodušené momenty proto dávají stejný výsledek a není nutné omezovat výpočty pouze pro potenciály dipólu, kvadrupólu a oktupolu. Je to výhoda pohledu tenzoru, a nejen to. ${\ displaystyle {f} (\ mathbf {r})}$${\ displaystyle {\ boldsymbol {\ otimes}} r^{l}}$${\ displaystyle \ mathbf {T} ^{(l)}}$

Operátor Efimovova žebříku

Sférické funkce mají několik opakujících se vzorců. V kvantové mechanice hrají roli rekurentní vzorce, když spojují funkce kvantových stavů pomocí žebříkového operátoru . K vlastnosti došlo kvůli skupině symetrií uvažovaného systému. Vektorový žebříčkový operátor pro invariantní harmonické stavy nalezené v papíru a podrobně popsané v. ${\ Displaystyle \ psi -}$

Za tímto účelem se použije transformace -prostoru, která zachová formu Laplaceovy rovnice:${\ displaystyle {\ boldsymbol {\ rho}}}$

${\ displaystyle {\ boldsymbol {\ rho}} = {\ frac {\ \ mathbf {r}} {r^{2}}}.}$

Operátor aplikující na potenciál harmonického tenzoru v prostoru přechází do Efimovova operátoru žebříku působícího na transformovaný tenzor v prostoru: ${\ displaystyle {\ boldsymbol {\ nabla}}}$${\ displaystyle {\ boldsymbol {\ rho}}}$${\ displaystyle \ mathbf {r}}$

${\ displaystyle {\ hat {\ mathbf {D}}} = (2 {\ hat {l}} -1) \ mathbf {r} -r^{2} {\ boldsymbol {\ nabla}},}$

kde je operátor modulu momentu hybnosti : ${\ displaystyle {\ hat {l}}}$

${\ displaystyle {\ hat {l}} = ({\ boldsymbol {\ nabla}} \ mathbf {r}).}$

Obslužné násobí harmonické tenzor jeho studia IE , pokud připomenout podle kulový funkci kvantových čísel , . Chcete -li zkontrolovat činnost operátora žebříku , můžete jej použít na tenzory dipólových a čtyřpólových: ${\ displaystyle {\ hat {l}}}$${\ Displaystyle l}$ ${\ Displaystyle l}$${\ displaystyle m}$${\ displaystyle \ mathbf {\ hat {D}}}$

${\ Displaystyle \ mathbf {\ hat {D}} _ {i} x_ {k} = 3x_ {i} x_ {k}-\ delta _ {ik},}$

${\ Displaystyle \ mathbf {\ hat {D}} _ {i} x_ {k} x_ {n} = 15x_ {i} x_ {k} x_ {n} -3 \ delta _ {ik} x_ {n}- 3 \ delta _ {kn} x_ {i} -3 \ delta _ {ni} x_ {k},}$

Uplatňování postupně se dostaneme celkový tvar neměnných harmonických tensors: ${\ displaystyle \ mathbf {\ hat {D}}}$${\ displaystyle \ mathbf {1}}$

${\ Displaystyle \ mathbf {T} ^{(l)} = (\ otimes \ mathbf {\ hat {D}}) ^{l} \ mathbf {1}.}$

Operátor analogický s operátorem žebříku oscilátoru . Ke sledování vztahu s kvantovým operátorem je užitečné znásobit jej tím, že přejdete do obráceného prostoru: ${\ displaystyle \ mathbf {\ hat {D}}}$ ${\ displaystyle i \ hbar}$

${\ displaystyle {\ boldsymbol {\ rho}} = {\ frac {\ mathbf {r}} {r^{2}}}.}$

V důsledku toho operátor přejde do operátoru hybnosti v prostoru: ${\ displaystyle {\ boldsymbol {\ rho}}}$

${\ Displaystyle \ mathbf {\ hat {D}} \ Rightarrow \ mathbf {\ hat {p}}.}$

Je užitečné použít následující vlastnosti . ${\ displaystyle \ mathbf {\ hat {D}}}$

• Komutátor operátorů souřadnic je nulový:
  $${\ Displaystyle {\ hat {D}} _ {i} {\ hat {D}} _ {k}-{\ hat {D}} _ {k} {\ hat {D}} _ {i} = 0 .}$$

  

Tato nemovitost je velmi vhodná pro výpočty.

• Produkt skalárního operátoru je v prostoru harmonických funkcí nulový:
  $${\ Displaystyle {\ hat {D}} _ {i} {\ hat {D}} _ {i} = {\ hat {\ mathbf {D}}} {\ hat {\ mathbf {D}}} = r ^{4} \ Delta.}$$

  

Tato vlastnost dává nulovou stopu harmonického tenzoru přes každé dva indexy. ${\ displaystyle \ mathbf {T} ^{l}}$

Operátor žebříku je analogický tomu v problému kvantového oscilátoru . Generuje Glauberovy stavy, které jsou vytvořeny v kvantové teorii polí elektromagnetického záření. Později se jako teoretický výsledek ukázalo, že koherentní stavy jsou vlastní každému kvantovému systému se skupinovou symetrií zahrnující rotační skupinu.

Neměnná forma sférických harmonických

Sférické harmonické jsou v souladu se systémem souřadnic. Dovolit být na jednotkové vektory podél osy X, Y, Z. naznačovat následujících jednotkových vektorů as a : ${\ Displaystyle \ mathbf {n} _ {x}, \ mathbf {n} _ {y}, \ mathbf {n} _ {z}}$${\ displaystyle \ mathbf {n} _ {+}}$${\ displaystyle \ \ mathbf {n} _ {-}}$

${\ Displaystyle \ mathbf {n} _ {\ pm} = {\ frac {(\ mathbf {n} _ {x} \ pm i \ mathbf {n} _ {y})} {\ sqrt {2}}} .}$

Pomocí vektorů jsou pevné harmonické rovny:

${\ Displaystyle r ^{l} Y _ {(l \ pm m)} = C_ {l, m} (\ mathbf {n} _ {z} \ mathbf {\ hat {D)}} ^{(lm)} (\ mathbf {n} _ {\ pm} \ mathbf {\ hat {D)}} ^{m} \ mathbf {1} = C_ {l, m} \ left [\ mathbf {M} ^{(l) } \ otimes \ mathbf {n_ {z}} ^{(lm)} \ otimes \ mathbf {n _ {\ pm}} ^{m} \ right]}$

kde je konstanta: ${\ displaystyle C_ {l, m}}$

${\ Displaystyle C_ {l, m} = {\ frac {2^{m \ setminus 2} {\ sqrt {2l+1}}} {\ sqrt {(l+m)! (lm)!}}}}$

Moment hybnosti je definován rotační skupinou. Mechanická hybnost souvisí s překladovou skupinou. Operátor žebříku je mapování hybnosti při inverzi 1/ r 3-d prostoru. Je zvyšování operátora . Operátor snížení zde je přirozeně gradient spolu s částečnou kontrakcí přes párové indexy, aby ostatní zůstali: ${\ displaystyle \ mathbf {\ hat {L}}}$${\ displaystyle \ mathbf {\ hat {p}}}$${\ displaystyle i}$

${\ Displaystyle \ left [\ partial x_ {i} \ mathbf {T} _ {i} ^{(l-1)} \ right] = (2l+1) l \, \ mathbf {T} ^{(l -1)}}$

Spektrální analýza

Výkonové spektrum při zpracování signálu

Celkový výkon funkce f je v literatuře zpracování signálu definován jako integrál funkce na druhou, děleno oblastí její domény. Pomocí vlastností ortonormality kulových harmonických funkcí skutečné jednotkové síly je snadné ověřit, že celkový výkon funkce definované v jednotkové sféře souvisí s jejím spektrálními koeficienty zobecněním Parsevalovy věty (zde je věta uvedena u Schmidtových semi-normalizovaných harmonických je vztah mírně odlišný pro ortonormální harmonické):

${\ Displaystyle {\ frac {1} {4 \, \ pi}} \ int _ {\ Omega} | f (\ Omega) |^{2} \, d \ Omega = \ sum _ {\ ell = 0} ^{\ infty} S_ {f \! f} (\ ell),}$

kde

${\ Displaystyle S_ {f \! f} (\ ell) = {\ frac {1} {2 \ ell +1}} \ sum _ {m =-\ ell}^{\ ell} | f _ {\ ell m } |^{2}}$

je definováno jako spektrum úhlového výkonu (u Schmidtových polonormalizovaných harmonických). Podobným způsobem lze definovat křížovou sílu dvou funkcí jako

${\ Displaystyle {\ frac {1} {4 \, \ pi}} \ int _ {\ Omega} f (\ Omega) \, g^{\ ast} (\ Omega) \, d \ Omega = \ sum _ {\ ell = 0}^{\ infty} S_ {fg} (\ ell),}$

kde

${\ Displaystyle S_ {fg} (\ ell) = {\ frac {1} {2 \ ell +1}} \ sum _ {m =-\ ell}^{\ ell} f _ {\ ell m} g _ {\ vše m}^{\ ast}}$

je definováno jako spektrum křížové energie. Pokud funkce f a g mají nulový průměr (tj. Spektrální koeficienty f ₀₀ a g ₀₀ jsou nulové), pak S _ff ( ℓ ) a S _fg ( ℓ ) představují příspěvky k variance a kovarianci funkce pro stupeň ℓ , resp. Je běžné, že (křížové) výkonové spektrum je dobře aproximováno mocninovým zákonem formy

${\ Displaystyle S_ {f \! f} (\ ell) = C \, \ ell ^{\ beta}.}$

Když β  = 0, spektrum je „bílé“, protože každý stupeň má stejnou sílu. Když β  <0, spektrum se nazývá "červené", protože v nízkých stupních s dlouhými vlnovými délkami je více energie než ve vyšších stupních. Nakonec, když β  > 0, spektrum se nazývá „modré“. Podmínka na pořadí růstu S _ff ( ℓ ) souvisí s pořadím diferencovatelnosti f v další části.

Vlastnosti odlišnosti

Je také možné pochopit vlastnosti diferencovatelnost původní funkce f , pokud jde o asymptotics z S _FF ( litrů, ). Zejména, je-li S _ff ( ℓ ) se rozkládá rychleji než racionální funkce z pásmy jako pásmy  ® ¥, pak f je nekonečně diferencovatelná . V případě, dále S _FF ( ℓ ) se rozkládá exponenciálně, pak f je skutečně reálný analytická na kouli.

Obecnou technikou je použít teorii Sobolevových prostorů . Prohlášení týkající růst S _FF ( litrů, ) na diferencovatelnost jsou pak podobné analogických výsledků na růst koeficientů Fourierovy řady . Konkrétně pokud

${\ Displaystyle \ sum _ {\ ell = 0}^{\ infty} (1+ \ ell^{2})^{s} S_ {ff} (\ ell) <\ infty,}$

pak f je v Sobolevově prostoru H ^s ( S ² ). Sobolevova věta o vložení zejména naznačuje, že f je nekonečně diferencovatelné za předpokladu, že

${\ Displaystyle S_ {ff} (\ ell) = O (\ ell ^{-s}) \ quad {\ rm {{as \} \ ell \ to \ infty}}}$

pro všechny s .

Algebraické vlastnosti

Věta o sčítání

Matematický výsledek značného zájmu a využití se nazývá adiční věta pro sférické harmonické. Vzhledem k tomu, dva vektory r a r‘ , s sférických souřadnic a , v tomto pořadí, je úhel mezi nimi je dána vztahem ${\ Displaystyle (r, \ theta, \ varphi)}$${\ Displaystyle (r ', \ theta', \ varphi ')}$${\ displaystyle \ gamma}$

${\ Displaystyle \ cos \ gamma = \ cos \ theta '\ cos \ theta +\ sin \ theta \ sin \ theta' \ cos (\ varphi -\ varphi ')}$

ve kterém roli goniometrických funkcí objevujících se na pravé straně hrají sférické harmonické a na levé straně hrají Legendrovy polynomy .

Na přídavek věta uvádí,

${\ Displaystyle P _ {\ ell} (\ mathbf {x} \ cdot \ mathbf {y}) = {\ frac {4 \ pi} {2 \ ell +1}} \ sum _ {m =-\ ell}^ {\ ell} Y _ {\ ell m} (\ mathbf {y}) \, Y _ {\ ell m}^{*} (\ mathbf {x}) \ quad \ forall \, \ ell \ in \ mathbb {N } _ {0} \; \ forall \, \ mathbf {x}, \ mathbf {y} \ in \ mathbb {R} ^{2} \ colon \; \ | \ mathbf {x} \ | _ {2} = \ | \ mathbf {y} \ | _ {2} = 1 \ ,,}$

( 1 )

kde P _ℓ je Legendreův polynom stupně ℓ . Tento výraz platí pro skutečné i komplexní harmonické. Výsledek lze prokázat analyticky, použitím vlastností Poissonova jádra v jednotkové kouli, nebo geometricky aplikováním rotace na vektor y tak, aby směřoval podél osy z , a poté přímo vypočítat pravou stranu.

Zejména když x  =  y , dává to Unsöldovu větu

${\ Displaystyle \ sum _ {m =-\ ell}^{\ ell} Y _ {\ ell m}^{*} (\ mathbf {x}) \, Y _ {\ ell m} (\ mathbf {x}) = {\ frac {2 \ ell +1} {4 \ pi}}}$

který generalizuje identitu cos ² θ + sin ² θ = 1 na dvě dimenze.

V expanzi ( 1 ) je levá strana P _ℓ ( x ⋅ y ) konstantním násobkem stupně ℓ zonální sférické harmonické . Z tohoto pohledu má člověk následující zobecnění na vyšší dimenze. Nechť Y _j je libovolný ortonormální základ prostoru H _ℓ stupně ℓ sférických harmonických na n -sféře. Poté se stupeň ℓ zonální harmonické odpovídající jednotkovému vektoru x rozloží jako ${\ displaystyle Z _ {\ mathbf {x}}^{(\ ell)}}$

${\ Displaystyle Z _ {\ mathbf {x}}^{(\ ell)} ({\ mathbf {y}}) = \ sum _ {j = 1}^{\ dim (\ mathbf {H} _ {\ ell })} {\ overline {Y_ {j} ({\ mathbf {x}})}}} \, Y_ {j} ({\ mathbf {y}})}$

( 2 )

Kromě toho je zónová harmonická uvedena jako konstantní násobek příslušného Gegenbauerova polynomu : ${\ displaystyle Z _ {\ mathbf {x}}^{(\ ell)} ({\ mathbf {y}})}$

${\ Displaystyle Z _ {\ mathbf {x}}^{(\ ell)} ({\ mathbf {y}}) = C _ {\ ell}^{((n-2)/2)} ({\ mathbf { x}} \ cdot {\ mathbf {y}})}$

( 3 )

Kombinace ( 2 ) a ( 3 ) dává ( 1 ) v rozměru n = 2, když x a y jsou reprezentovány v sférických souřadnicích. Nakonec vyhodnocení na x = y dává funkční identitu

${\ Displaystyle {\ frac {\ dim \ mathbf {H} _ {\ ell}} {\ omega _ {n-1}}} = \ sum _ {j = 1}^{\ dim (\ mathbf {H} _ {\ ell})} | Y_ {j} ({\ mathbf {x}}) |^{2}}$

kde ω _{n −1} je objem sféry ( n −1).

Pravidlo kontrakce

Další užitečná identita vyjadřuje součin dvou sférických harmonických jako součet sférických harmonických

${\ Displaystyle Y_ {a, \ alpha} \ left (\ theta, \ varphi \ right) Y_ {b, \ beta} \ left (\ theta, \ varphi \ right) = {\ sqrt {\ frac {\ left ( 2a+1 \ right) \ left (2b+1 \ right)} {4 \ pi}}} \ sum _ {c, \ gamma} \ left (-1 \ right)^{\ gamma} {\ sqrt {2c +1}} \ left ({\ begin {array} {ccc} a & b & c \\\ alpha & \ beta &-\ gamma \ end {array}} \ right) \ left ({\ begin {array} {ccc} a & b & c \\ 0 & 0 & 0 \ end {array}} \ right) Y_ {c, \ gamma} \ left (\ theta, \ varphi \ right)}$

kde hodnoty a jsou určeny pravidly výběru pro symboly 3j . ${\ displaystyle c}$${\ displaystyle \ gamma}$

Clebsch -Gordanovy koeficienty

Clebsch -Gordanovy koeficienty jsou koeficienty objevující se v expanzi součinu dvou sférických harmonických z hlediska samotných sférických harmonických. K provedení v podstatě stejného výpočtu je k dispozici řada technik, včetně Wignerova 3-jm symbolu , Racahových koeficientů a Slaterových integrálů . Abstraktně, koeficienty Clebsch-Gordan vyjadřují tensor produkt dvou ireducibilních reprezentací ze skupiny otáčení jako součet ireducibilních reprezentací: vhodně normalizovaných, koeficienty jsou potom multiplicity.

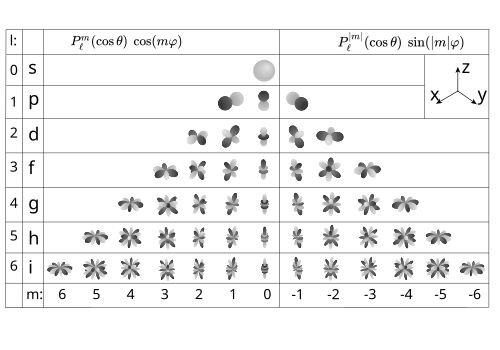
Vizualizace sférických harmonických

Laplaceovy sférické harmonické mohou být vizualizovány zvážením jejich „ uzlových čar “, tj. Množiny bodů na kouli kde , nebo alternativně kde . Uzlové řádky jsou složeny z ℓ kruhů: existuje | m | kruhy podél zeměpisných délek a ℓ - | m | kruhy podél zeměpisných šířek. Jeden může určit počet uzlových linií každého typu spočítáním počtu nul v uživatelské a směrech, resp. Vzhledem k tomu , že každá z těchto funkcí obsahuje skutečné a imaginární složky přidružených Legendrových polynomů ℓ - | m | nuly, z nichž každá vede k uzlové „linii zeměpisné šířky“. Na druhou stranu, vzhledem k tomu, že funkce jako trigonometrický sin a cos mají 2 | m | nuly, z nichž každá dává vzniknout uzlové „zeměpisné délce“. ${\ displaystyle Y _ {\ ell}^{m}}$${\ Displaystyle \ Re [Y _ {\ ell}^{m}] = 0}$${\ Displaystyle \ Im [Y _ {\ ell}^{m}] = 0}$${\ displaystyle Y _ {\ ell}^{m}}$${\ displaystyle Y _ {\ ell}^{m}}$${\ displaystyle \ theta}$${\ Displaystyle \ varphi}$${\ displaystyle Y _ {\ ell}^{m}}$${\ displaystyle \ theta}$${\ displaystyle Y _ {\ ell}^{m}}$${\ Displaystyle \ varphi}$

Když je sférický harmonický řád m nula (na obrázku vlevo nahoře), sférické harmonické funkce nezávisí na zeměpisné délce a označují se jako zónové . Tyto sférické harmonické jsou zvláštním případem zonálních sférických funkcí . Když ℓ  = | m | (vpravo dole na obrázku), neexistují žádné nulové přechody v zeměpisné šířce a funkce jsou označovány jako sektorové . V ostatních případech funkce kontrolují sféru a jsou označovány jako tesseral .

Obecnější sférické harmonické stupně ℓ nemusí být nutně na Laplaceově základě a jejich uzlové množiny mohou být docela obecného druhu. ${\ displaystyle Y _ {\ ell}^{m}}$

Seznam sférických harmonických

Analytické výrazy pro prvních několik ortonormalizovaných Laplaceových sférických harmonických, které používají konvenci fází Condon – Shortley: ${\ Displaystyle Y _ {\ ell}^{m}: S^{2} \ to \ mathbb {C}}$

Vyšší rozměry

Klasické sférické harmonické jsou definovány jako komplexní funkce v jednotkové sféře v trojrozměrném euklidovském prostoru . Sférické harmonické lze zobecnit na vyšší dimenzionální euklidovský prostor následujícím způsobem, což vede k funkcím . Nechť P _ℓ označuje prostor komplexních homogenních polynomů stupně ℓ v n reálných proměnných, které jsou zde považovány za funkce . To znamená, že polynom p je v P _ℓ za předpokladu, že pro jakýkoli reálný má ${\ displaystyle S^{2}}$${\ displaystyle \ mathbb {R} ^{3}}$${\ displaystyle \ mathbb {R} ^{n}}$${\ Displaystyle S^{n-1} \ to \ mathbb {C}}$${\ Displaystyle \ mathbb {R} ^{n} \ to \ mathbb {C}}$${\ Displaystyle \ lambda \ in \ mathbb {R}}$

${\ Displaystyle p (\ lambda \ mathbf {x}) = \ lambda ^{\ ell} p (\ mathbf {x}).}$

Nechť A _ℓ označuje podprostor P _ℓ skládající se ze všech harmonických polynomů :

${\ Displaystyle \ mathbf {A} _ {\ ell}: = \ {p \ in \ mathbf {P} _ {\ ell} \, \ mid \, \ Delta p = 0 \} \ ,.}$

Toto jsou (pravidelné) pevné sférické harmonické . Nechť H _ℓ označuje prostor funkcí na jednotkové sféře

${\ Displaystyle S ^{n-1}: = \ {\ mathbf {x} \ in \ mathbb {R} ^{n} \, \ mid \, \ left | x \ right | = 1 \}}$

získané restrikcí z A _ℓ

${\ Displaystyle \ mathbf {H} _ {\ ell}: = \ left \ {f: S^{n-1} \ to \ mathbb {C} \, \ mid \, {\ text {for some}} p \ in \ mathbf {A} _ {\ ell}, \, f (\ mathbf {x}) = p (\ mathbf {x}) {\ text {pro všechny}} \ mathbf {x} \ v S^{ n-1} \ vpravo \}.}$

Platí následující vlastnosti:

• Součet prostorů H _ℓ je hustý v sadě spojitých funkcí na vzhledem k jednotné topologii , podle Stone -Weierstrassovy věty . V důsledku toho je součet těchto prostorů také hustý v prostoru L ² ( S ^{n −1} ) čtvercově integrovatelných funkcí na kouli. Každá čtvercově integrovatelná funkce na kouli se tedy jedinečně rozkládá na řadu sférických harmonických, kde se řada sbíhá ve smyslu L ² .${\ Displaystyle C (S^{n-1})}$${\ Displaystyle S^{n-1}}$
• Pro všechny f  ∈  H _ℓ , jeden má
  $${\ Displaystyle \ Delta _ {S^{n-1}} f =-\ ell (\ ell +n-2) f.}$$

  
  kde Δ _{S ^{n −1}} je operátor Laplace – Beltrami na S ^{n −1} . Tento operátor je analogem úhlové části Laplacianu ve třech rozměrech; to znamená, že Laplacian v n rozměrech se rozkládá jako
  $${\ Displaystyle \ nabla^{2} = r^{1-n} {\ frac {\ částečná} {\ částečná r}} r^{n-1} {\ frac {\ částečná} {\ částečná r}} +r^{-2} \ Delta _ {S^{n-1}} = {\ frac {\ částečný^{2}} {\ částečný r^{2}}}+{\ frac {n-1} {r}} {\ frac {\ částečný} {\ částečný r}}+r^{-2} \ Delta _ {S^{n-1}}}$$

  
• Ze Stokesovy věty a předchozí vlastnosti vyplývá, že prostory H _ℓ jsou ortogonální vzhledem k vnitřnímu součinu z L ² ( S ^{n −1} ). To znamená,
  $${\ Displaystyle \ int _ {S^{n-1}} f {\ bar {g}} \, \ mathrm {d} \ Omega = 0}$$

  
  pro f  ∈  H _ℓ a g  ∈  H _k pro k  ≠  ℓ .
• Naopak prostory H _ℓ jsou přesně vlastní prostory Δ _{S ^{n −1}} . Zejména aplikace spektrální věty na Rieszův potenciál poskytuje další důkaz, že prostory H _ℓ jsou párově ortogonální a úplné v L ² ( S ^{n −1} ).${\ Displaystyle \ Delta _ {S^{n-1}}^{-1}}$
• Každý homogenní polynom p  ∈  P _ℓ lze jedinečně zapsat do formuláře
  $${\ Displaystyle p (x) = p _ {\ ell} (x)+| x |^{2} p _ {\ ell -2}+\ cdots+{\ begin {cases} | x |^{\ ell} p_ {0} & \ ell {\ rm {\ even}} \\ | x |^{\ ell -1} p_ {1} (x) & \ ell {\ rm {\ odd}} \ end {cases}} }$$

  
  kde p _j  ∈  A _j . Zejména,
  $${\ Displaystyle \ dim \ mathbf {H} _ {\ ell} = {\ binom {n+\ ell -1} {n-1}}-{\ binom {n+\ ell -3} {n-1}}. }$$

  

Ortogonální základ sférických harmonických ve vyšších dimenzích lze konstruovat induktivně metodou separace proměnných , řešením Sturm-Liouvilleova problému pro sférický Laplacián

${\ Displaystyle \ Delta _ {S ^{n-1}} = \ sin ^{2-n} \ varphi {\ frac {\ partial} {\ partial \ varphi}} \ sin ^{n-2} \ varphi {\ frac {\ partial} {\ částečné \ varphi}}+\ sin ^{-2} \ varphi \ Delta _ {S ^{n-2}}}$

kde φ je osová souřadnice v sférickém souřadném systému na S ^{n −1} . Konečným výsledkem takového postupu je

${\ Displaystyle Y _ {\ ell _ {1}, \ dots \ ell _ {n-1}} (\ theta _ {1}, \ dots \ theta _ {n-1}) = {\ frac {1} { \ sqrt {2 \ pi}}} e^{i \ ell _ {1} \ theta _ {1}} \ prod _ {j = 2}^{n-1} {} _ {j} {\ bar { P}} _ {\ ell _ {j}}^{\ ell _ {j-1}} (\ theta _ {j})}$

kde indexy splňují | ℓ ₁ | ≤ ℓ ₂ ≤ ⋯ ≤ ℓ _{n −1} a vlastní hodnota je - ℓ _{n −1} ( ℓ _{n −1} + n −2). Funkce v produktu jsou definovány ve smyslu funkce Legendre

${\ displaystyle {} _ {j} {\ bar {P}} _ {L}^{\ ell} (\ theta) = {\ sqrt {{\ frac {2L+j-1} {2}} {\ frac {(L+\ ell+j-2)!} {(L- \ ell)!}}}} \ sin ^{\ frac {2-j} {2}} (\ theta) P_ {L+{\ frac {j-2} {2}}}^{-\ left (\ ell +{\ frac {j-2} {2}} \ right)} (\ cos \ theta) \ ,.}$

Souvislost s teorií reprezentace

Prostor H _ℓ sférických harmonických studia pásmy je znázornění symetrie skupiny rotací kolem bodu ( SO (3) ) a jeho dvojitého víka SU (2) . Rotace skutečně působí na dvojrozměrnou sféru , a tedy také na H _ℓ podle složení funkce

${\ Displaystyle \ psi \ mapsto \ psi \ circ \ rho ^{-1}}$

pro ψ sférickou harmonickou a ρ rotaci. Reprezentace H _ℓ je neredukovatelná reprezentace SO (3).

Prvky H _ℓ vznikají jako omezení sféry prvků A _ℓ : harmonické polynomy homogenní stupně ℓ na trojrozměrném euklidovském prostoru R ³ . Tím, polarizace o ln  ∈  A _pásmy , jsou koeficienty symetrický na indexy, jednoznačně určen požadavkem ${\ displaystyle \ psi _ {i_ {1} \ dots i _ {\ ell}}}$

${\ Displaystyle \ psi (x_ {1}, \ dots, x_ {n}) = \ sum _ {i_ {1} \ dots i _ {\ ell}} \ psi _ {i_ {1} \ dots i _ {\ ell }} x_ {i_ {1}} \ cdots x_ {i _ {\ ell}}.}$

Podmínka, že ψ být harmonický, je ekvivalentní tvrzení, že tenzor musí být stopově volný na každém páru indexů. Jako neredukovatelná reprezentace SO (3) je tedy H _ℓ izomorfní k prostoru beze stop symetrických tenzorů stupně ℓ . ${\ displaystyle \ psi _ {i_ {1} \ dots i _ {\ ell}}}$

Obecněji platí, že analogická tvrzení platí ve vyšších dimenzích: prostor H _ℓ sférických harmonických na n -sféře je neredukovatelná reprezentace SO ( n +1) odpovídající bezeztrátovým symetrickým ℓ -tenzorům. Avšak zatímco každá neredukovatelná tenzorová reprezentace SO (2) a SO (3) je tohoto druhu, speciální ortogonální skupiny ve vyšších dimenzích mají další neredukovatelné reprezentace, které tímto způsobem nevznikají.

Speciální ortogonální skupiny mají další rotační reprezentace, které nejsou tenzorovými reprezentacemi a obvykle nejsou sférickými harmonickými. Výjimkou jsou rotační vyjádření SO (3): v přísném slova smyslu se jedná o reprezentace dvojitého krytu SU (2) SO (3). Na druhé straně, SU (2) je identifikován se skupinou jednotkových kvaternionů , a tak se shoduje s 3-sférou . Prostory sférických harmonických na 3 sféře jsou určitými spinovými reprezentacemi SO (3), s ohledem na působení kvartérním násobením.

Spojení s hemisférickými harmonickými

Sférické harmonické lze rozdělit na dvě sady funkcí. Jednou z nich jsou hemisférické funkce (HSH), ortogonální a kompletní na polokouli. Další jsou komplementární hemisférické harmonické (CHSH).

Zobecnění

Tyto úhlové-zachování symetrie z dvou-koule jsou popsány skupinou Möbius transformací PSL (2, C ). S ohledem na tuto skupinu je koule ekvivalentní obvyklé Riemannově kouli . Skupina PSL (2, C ) je izomorfní k (vlastní) Lorentzově skupině a její působení na dvě sféry souhlasí s působením Lorentzovy skupiny na nebeskou sféru v Minkowského prostoru . Analog sférických harmonických pro Lorentzovu skupinu je dán hypergeometrickou řadou ; dále lze sférické harmonické znovu vyjádřit pomocí hypergeometrických řad, protože SO (3) = PSU (2) je podskupina PSL (2, C ).

Obecněji lze hypergeometrické řady zobecnit, aby popsaly symetrie jakéhokoli symetrického prostoru ; zejména lze vyvinout hypergeometrické řady pro jakoukoli Lieovu skupinu .

Viz také

Poznámky

Reference

Citované reference

• Courant, Richard ; Hilbert, David (1962), Metody matematické fyziky, svazek I , Wiley-Interscience.
• Edmonds, AR (1957), Angular Momentum in Quantum Mechanics , Princeton University Press, ISBN 0-691-07912-9
• Eremenko, Alexandre; Jakobson, Dmitry; Nadirashvili, Nikolai (2007), „O uzlových souborech a uzlových doménách na S² a R²“ , Annales de l'Institut Fourier , 57 (7): 2345–2360, doi : 10,5802/aif.2335 , ISSN  0373-0956 , MR  2394544
• Hall, Brian C. (2013), Quantum Theory for Mathematicians , Graduate Texts in Mathematics, 267 , Springer, ISBN 978-1461471158
• MacRobert, TM (1967), Sférické harmonické: Elementární pojednání o harmonických funkcích, s aplikacemi , Pergamon Press.
• Meijer, Paul Herman Ernst; Bauer, Edmond (2004), Teorie skupiny: Aplikace na kvantovou mechaniku , Dover, ISBN 978-0-486-43798-9.
• Solomentsev, ED (2001) [1994], „Sférické harmonické“ , encyklopedie matematiky , EMS Press.
• Stein, Elias ; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces , Princeton, New Jersey: Princeton University Press, ISBN 978-0-691-08078-9.
• Unsöld, Albrecht (1927), „Beiträge zur Quantenmechanik der Atome“, Annalen der Physik , 387 (3): 355–393, Bibcode : 1927AnP ... 387..355U , doi : 10,1002/andp.19273870304.
• Whittaker, ET ; Watson, GN (1927), Kurz moderní analýzy , Cambridge University Press , s. 392.

Obecné reference

• EW Hobson, Teorie sférických a elipsoidních harmonických , (1955) Chelsea Pub. Co., ISBN  978-0-8284-0104-3 .
• C. Müller, Spherical Harmonics , (1966) Springer, Lecture Notes in Mathematics, Vol. 17, ISBN  978-3-540-03600-5 .
• EU Condon a GH Shortley, Theory of Atomic Spectra , (1970) Cambridge na University Press, ISBN  0-521-09209-4 , Viz kapitola 3 .
• JD Jackson, Classical Electrodynamics , ISBN  0-471-30932-X
• Albert Messiah, kvantová mechanika , svazek II. (2000) Dover. ISBN  0-486-40924-4 .
• Stiskněte, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), „Oddíl 6.7. Sférické harmonické“ , Numerical Recipes: The Art of Scientific Computing (3. vyd.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
• DA Varshalovich, AN Moskalev, VK Khersonskii Quantum Theory of Angular Momentum , (1988) World Scientific Publishing Co., Singapore, ISBN  9971-5-0107-4
• Weisstein, Eric W. „Sférické harmonické“ . MathWorld .
• Maddock, John, Sférické harmonické v Boost.Math