Objektivní funkce - Surjective function

V matematice je surjektivní funkce (také známá jako přerušení nebo funkce ) funkce $f,$ která mapuje prvek $x$ na každý prvek $y$ ; to znamená, že pro každé $y$ existuje $x$ takové, že $f (x) = y$ . Jinými slovy, každý prvek Funkce je codomain je obraz z alespoň jednoho prvku svém oboru . Není požadováno, aby $x$ bylo jedinečné ; funkce $f$ může Pro jeden nebo více prvků z $X$ do stejného prvku $Y$ .

Neinjektivní surjektivní funkce (surjekce, nikoli bijekce)
Injektivní surjektivní funkce (bijekce)
Injektivní nesurjektivní funkce (injekce, nikoli bijekce)
Non-injektivní non-surjektivní funkce (také ne bijekce)

Pojem surjektiv a související pojmy injektivní a bijektivní zavedl Nicolas Bourbaki , skupina převážně francouzských matematiků 20. století, kteří pod tímto pseudonymem napsali řadu knih představujících výklad moderní vyspělé matematiky, počínaje rokem 1935. Francouzská slovo sur znamená nad nebo nad a souvisí se skutečností, že obraz domény surjektivní funkce zcela pokrývá doménu funkce.

Jakákoli funkce vyvolává překvapení tím, že omezí svou doménu na obraz své domény. Každá surjektivní funkce má správnou inverzi a každá funkce s pravou inverzí je nutně předpokladem. Složení of surjektivní funkcí je vždy surjective. Jakákoli funkce může být rozložena na přeliv a injekci.

Definice

Zobrazení na je funkce , jejíž obraz se rovná jeho codomain . Ekvivalentně funkce s doménou a codomain surjective jestliže ke každému v existuje alespoň jeden na s . Projekce jsou někdy označeny dvouhlavou pravou šipkou ( U+ 21A0 ↠ PRAVÉ DVORY ŠIPKA S HLAVOU ), jako v . ${\ displaystyle f}$ ${\ displaystyle X}$ ${\ displaystyle Y}$ ${\ displaystyle y}$ ${\ displaystyle Y}$ ${\ displaystyle x}$ ${\ displaystyle X}$ ${\ Displaystyle f (x) = y}$ ${\ Displaystyle f \ colon X \ twoheadrightarrow Y}$

Symbolicky,

Pokud , pak se říká, že je surjektivní, pokud

{\ Displaystyle f \ colon X \ rightarrow Y}

{\ displaystyle f}

{\ Displaystyle \ forall y \ v Y, \, \ existuje x \ v X, \; \; f (x) = y}

.

Příklady

Non-Zobrazení na od domény X do codomain Y . Menší žlutý ovál uvnitř Y je obraz (také nazývaný rozsah ) f . Tato funkce není surjektivní, protože obrázek nevyplňuje celou doménu. Jinými slovy, Y je zbarveno ve dvou krocích: Za prvé, pro každé x v X je bod f ( x ) zbarven žlutě; Za druhé, všechny zbývající body v Y , které nejsou žluté, jsou zbarveny modře. Funkce f by byla surjektivní pouze tehdy, kdyby neexistovaly žádné modré body.

Pro libovolnou sadu X je identifikační funkce id _X na X surjektivní.
Funkce $f : Z \to {0, 1}$ definovaná f ( n ) = n mod 2 (to znamená, že sudá celá čísla jsou mapována na 0 a lichá celá čísla na 1) je surjektivní.
Funkce $f : R \to R$ definovaná f ( x ) = 2 x + 1 je surjektivní (a dokonce bijektivní ), protože pro každé reálné číslo y máme x takové, že f ( x ) = y : takové vhodné x je ( y - 1)/2.
Funkce $f : R \to R$ definovaný f ( x ) = x ³ - 3 x surjective, protože předem Obraz jakékoliv reálné číslo y je množina řešení kubické rovnice polynomial x ³ - 3 x - y = 0 , a každý krychlový polynom se skutečnými koeficienty má alespoň jeden skutečný kořen. Tato funkce však není injektivní (a tedy ani bijektivní ), protože například předobraz y = 2 je { x = −1, x = 2}. (Ve skutečnosti má předobraz této funkce pro každé y , −2 ≤ y ≤ 2 více než jeden prvek.)
Funkce $g : R \to R$ je definován g ( x ) = x ² je ne surjektivní, protože není reálné číslo x tak, že x ² = -1 . Funkce $g : R \to R \geq0$ definovaná $g (x) = x 2$ (s omezenou doménou) je však surjektivní, protože pro každé y v nezáporné skutečné doméně Y existuje ve skutečné doméně alespoň jedno x X takové, že x ² = y .
Přirozený logaritmus funkce $ln: (0, + \infty) \to R$ je surjektivní a dokonce bijektivní (mapování ze souboru pozitivních reálných čísel do množiny všech reálných čísel). Jeho inverzní, exponenciální funkce , pokud je definována sadou reálných čísel jako doménou, není surjektivní (protože její rozsah je množina kladných reálných čísel).
Matice exponenciální není surjektivní při pohledu jako mapa z prostoru všech n x n matic k sobě. Obvykle je však definována jako mapa z prostoru všech n × n matic do obecné lineární skupiny stupně n (tj. Skupiny všech n × n invertibilních matic ). Pod touto definicí je exponenciální matice surjektivní pro komplexní matice, i když stále není surjektivní pro skutečné matice.
Projekce z kartézského produktu $x$ $B$ do jednoho z jeho faktorů je surjektivní, pokud jiný faktor je prázdný.
Ve 3D videohře se vektory promítají na 2D plochou obrazovku pomocí surjektivní funkce.

Interpretace pro surjektivní funkce v karteziánské rovině, definované mapováním f : X → Y , kde y = f ( x ), X = doména funkce, Y = rozsah funkce. Každý prvek v rozsahu je mapován na z prvku v doméně podle pravidla f . Může existovat řada prvků domény, které se mapují na stejný prvek rozsahu. To znamená, že každé y v Y je mapováno z prvku x v X , více než jedno x může být mapováno na stejné y . Vlevo: Je zobrazena pouze jedna doména, která je f surjektivní. Vpravo: jsou zobrazeny dvě možné domény X ₁ a X ₂ .

Non-surjektivní funkce v karteziánské rovině. Ačkoli některé části funkce jsou surjektivní, kde prvky y v Y mají hodnotu x v X takovou, že y = f ( x ), některé části nejsou. Vlevo: Je y ₀ v Y , ale není tam žádný x ₀ v X tak, že y ₀ = f ( x ₀ ). Vpravo: Existuje y ₁ , y ₂ a y ₃ v Y , ale neexistují žádné x ₁ , x ₂ , a x ₃ v X, tak, že y ₁ = f ( x ₁ ), y ₂ = f ( x ₂ ), a y ₃ = f ( x ₃ ).

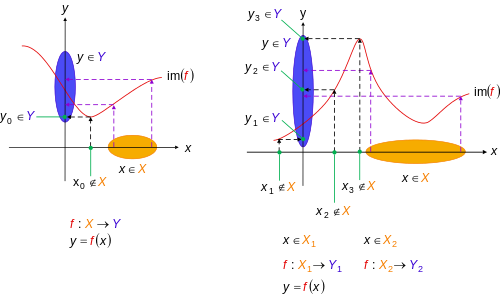
Vlastnosti

Funkce je bijektivní jen tehdy, je -li jak surjektivní, tak injektivní .

Pokud (jak se často dělá) je funkce identifikována svým grafem , pak surjektivita není vlastností samotné funkce, ale spíše vlastností mapování . To je funkce společně s její doménou. Na rozdíl od injektivity nelze surjektivitu vyčíst z grafu samotné funkce.

Projekce jako správné invertibilní funkce

O funkci g : Y → X se říká, že je pravou inverzí funkce f : X → Y, pokud f ( g ( y )) = y pro každé y v Y ( g lze vrátit zpět o f ). Jinými slovy, g je právo inverzní f v případě, že kompozice f o g o g a f v tomto pořadí, je funkce identity na doméně Y o g . Funkce g nemusí být úplný inverzní z F , protože kompozice v jiném pořadí, g o f , nemusí být funkce identity na doméně X o f . Jinými slovy, f může vrátit zpět nebo „ obrátit “ g , ale nemusí být nutně zrušeno.

Každá funkce s pravou inverzí je nutně nadsázka. Tvrzení, že každá surjektivní funkce má pravou inverzi, je ekvivalentní axiomu volby .

Pokud f : X → Y je surjektivní a B je podmnožina z Y , pak f ( f ^-1 ( B )) = B . Tak, B může být získána z jeho určení vzoru f ^-1 ( B ) .

Například v prvním výše uvedeném obrázku, je zde nějaká funkce g tak, že g ( C ) = 4. Tam je také nějaká funkce f tak, že f (4) = C . Nezáleží na tom, že g ( C ) se může rovnat také 3; záleží jen na tom, že f „obrátí“ g .

Objektivní složení: první funkce nemusí být surjektivní.
Další surjektivní funkce. (Tohle je náhoda )
Non -surjective funkce. (Tenhle je náhodou injekce )

Vyšetřování jako epimorfismy

Funkce f : X → Y je surjektivní tehdy a jen tehdy, je - li pravotočivá : dané jakékoli funkce g , h : Y → Z , kdykoli g o f = h o f , pak g = h . Tato vlastnost je formulován z hlediska funkcí a jejich složení a lze zobecnit na obecnější pojem k morphisms jednoho kategorie a jejich složení. Pravotočivé morfismy se nazývají epimorfismy . Surjektivní funkce jsou konkrétně epimorfismy v kategorii množin . Předpona epi je odvozena z řecké předložky ἐπί, což znamená nad , nahoře , na .

Jakýkoli morfismus s pravou inverzí je epimorfismus, ale opak není obecně pravdivý. Právo inverzní g z morfizmus f se nazývá část o f . Morfismus s pravou inverzí se nazývá rozdělený epimorfismus .

Projekce jako binární relace

Na jakoukoli funkci s doménou X a doménou Y lze pohlížet jako na levou celkovou a pravou jedinečnou binární relaci mezi X a Y její identifikací pomocí grafu její funkce . Surjektivní funkce s doménou X a doménou Y je pak binární relace mezi X a Y, která je pravá-jedinečná a jak levá celková, tak pravá celková .

Mohutnost domény očekávání

Mohutnost z oblasti surjective funkce je větší než nebo rovna mohutnosti jejího codomain: Je-li f : X → Y je Zobrazení na, pak X obsahuje alespoň tolik prvků, jako Y , ve smyslu kardinálních čísel . (Důkaz apeluje na zvolený axiom, aby ukázal, že funkce g : Y → X splňující f ( g ( y )) = y pro všechny y v Y existuje. G je snadno viditelné jako injektivní, takže formální definice | Y | ≤ | X | je splněno.)

Konkrétně, pokud oba X a Y jsou konečné se stejným počtem prvků, pak f : X → Y je surjektivní tehdy a jen tehdy, pokud f je injective .

Uvedené dvě sady X a Y , notace X ≤ ^* Y je říkával, že buď X je prázdný, nebo že je surjection z Y na X . Použitím axiomu volby lze ukázat, že X ≤ ^* Y a Y ≤ ^* X dohromady znamená, že | Y | = | X |, varianta Schröder – Bernsteinovy věty .

Složení a rozklad

Složení z surjektivní funkcí je vždy surjektivní: Je-li f a g jsou jak surjektivní a codomain ze g je rovno doméně f , pak f o g surjective. Naopak, pokud f o g je surjektivní, pak f je surjektivní (ale g , funkce aplikovaná jako první, nemusí být). Tyto vlastnosti zobecňují od odhadů v kategorii sad k jakýmkoli epimorfismům v jakékoli kategorii .

Libovolnou funkci lze rozložit na přeliv a injekci : Pro jakoukoli funkci h : X → Z existuje přeliv f : X → Y a injekce g : Y → Z taková, že h = g o f . Chcete -li to vidět, definujte Y jako množinu předobrazů h ⁻¹ ( z ), kde z je v h ( X ) . Tyto nalezení multivzorů jsou disjunktní a oddíl X . Potom f přenese každé x do prvku Y, který ho obsahuje, a g přenese každý prvek Y do bodu v Z, do kterého h posílá své body. Pak f je surjektivní, protože je to projekční mapa, a g je podle definice injektivní.

Indukované přelévání a indukovaná bijekce

Jakákoli funkce vyvolá překvapení tím, že omezí svou doménu na její rozsah. Jakákoli surjektivní funkce indukuje bijekci definovanou na kvocientu její domény sbalením všech mapování argumentů na daný pevný obrázek. Přesněji, každé přelití f : A → B může být zapracováno jako projekce následovaná bijekcí následovně. Nechť / ~ být třídy ekvivalence z A podle následujícího ekvivalence vztahu : x ~ y právě tehdy, když f ( x ) = f ( y ). Ekvivalentně je A /~ množina všech předobrazů pod f . Nechť P (~): A → A /~ je projekční mapa, která posílá každé x v A do své třídy ekvivalence [ x ] _~ , a nechť f _P : A /~ → B je dobře definovaná funkce daná f _P ([ x ] _~ ) = f ( x ). Potom f = f _P o P (~).

Viz také

Reference

Další čtení

Bourbaki, N. (2004) [1968]. Teorie množin . Prvky matematiky . 1 . Springer. doi : 10,1007/978-3-642-59309-3 . ISBN 978-3-540-22525-6. LCCN 2004110815 .

Languages

In other projects