Stromový automat - Tree automaton

Jiný pojem stromového automatu najdete v automatu na stromové chůzi .

Strom automat je druh státní mašinérie . Stromové automaty se zabývají spíše stromovými strukturami než řetězci konvenčních stavových strojů.

Následující článek se zabývá větvením stromových automatů, které odpovídají běžným jazykům stromů .

Stejně jako u klasických automatů může být automat s konečnými stromy (FTA) buď deterministický automat, nebo ne. Podle toho, jak automat zpracovává vstupní strom, mohou být automaty konečných stromů dvou typů: (a) zdola nahoru, (b) shora dolů. Toto je důležitý problém, protože i když nedeterministické (ND) zhora dolů a ND zdola nahoru automaty stromu jsou ekvivalentní v expresivní síle, deterministické automaty shora dolů jsou přísně méně silné než jejich deterministické protějšky zdola nahoru, protože vlastnosti stromu určené deterministickými stromovými automaty shora dolů mohou záviset pouze na vlastnostech cesty. (Deterministické stromové automaty zdola nahoru jsou stejně silné jako stromové automaty ND.)

Definice

Konečný strom automat zdola nahoru přes F je definován jako n-tice ( Q , F , Q , f , d), kde Q je množina stavů, F je zařazen abecedu (tj abeceda jehož symboly mají přidružené aritu ) , Q f ⊆ Q je množina konečných stavů a ​​Δ je sada přechodových pravidel tvaru f ( q 1 ( x 1 ), ..., q n ( x n )) → q ( f ( x 1 (..., x n )), pro n -ary f ∈ F , q , q i ∈ Q a x i proměnné označující podstromy. To znamená, že členové Δ jsou přepisovací pravidla z uzlů, jejichž kořeny dětí jsou stavy, do uzlů, jejichž kořeny jsou stavy. Stav uzlu je tedy odvozen ze stavů jeho podřízených.

Pro n = 0, to znamená pro konstantní symbol f , výše uvedená definice přechodového pravidla zní f () → q ( f ()); často jsou prázdné závorky pro pohodlí vynechány: f → q ( f ). Protože tato přechodová pravidla pro konstantní symboly (listy) nevyžadují stav, nejsou potřeba žádné výslovně definované počáteční stavy. Stromový automat zdola nahoru je spuštěn na základním členu nad F , přičemž začíná na všech jeho listech současně a pohybuje se nahoru, přičemž ke každému subtermu přiřazuje stav běhu od Q. Termín je přijat, pokud je jeho kořen přidružen k přijímajícímu stavu z Q f .

Shora dolů konečný strom automat přes F je definován jako n-tice ( Q , F , Q i , d), se dvěma rozdíly od zdola nahoru stromových automatů. Nejprve Q i ⊆ Q , množina jeho počátečních stavů, nahradí Q f ; zadruhé, jeho přechodová pravidla jsou orientována naopak: q ( f ( x 1 , ..., x n )) → f ( q 1 ( x 1 ), ..., q n ( x n )), pro n - ary f ∈ F , q , q i ∈ Q a x i proměnné označující podstromy. To znamená, že členové Δ zde přepisují pravidla z uzlů, jejichž kořeny jsou stavy, do uzlů, jejichž dětské kořeny jsou stavy. Automat shora dolů začíná v některých svých počátečních stavech u kořene a pohybuje se dolů po větvích stromu, asociuje podél běhu stav s každým subtermem indukčně. Strom je přijat, pokud lze touto cestou projít každou větev.

Stromový automat se nazývá deterministický (zkráceně DFTA ), pokud žádná dvě pravidla z Δ nemají stejnou levou stranu; jinak se nazývá nedeterministický ( NFTA ). Nedeterministické stromové automaty shora dolů mají stejnou vyjadřovací sílu jako nedeterministické zdola nahoru; přechodová pravidla se jednoduše obrátí a konečné stavy se stanou počátečními stavy.

Naproti tomu deterministické stromové automaty shora dolů jsou méně výkonné než jejich protějšky zdola nahoru, protože v deterministickém stromovém automatu nemají žádná dvě přechodová pravidla stejnou levou stranu. U stromových automatů jsou přechodová pravidla přepisovací pravidla; a u těch shora dolů budou na levé straně nadřazené uzly. V důsledku toho bude deterministický stromový automat shora dolů schopen testovat pouze vlastnosti stromu, které jsou pravdivé ve všech větvích, protože volba stavu pro zápis do každé podřízené větve je určena v nadřazeném uzlu, aniž by věděl obsah podřízených větví .

Příklady

Automat zdola nahoru přijímající booleovské seznamy

Využití barvení k rozlišení členů F a Q a použití seřazené abecedy F = { false , true , nil , cons (.,.)}, Přičemž cons má arity 2 a všechny ostatní symboly mají arity 0, strom zdola nahoru automat přijímající množinu všech konečných seznamů booleovských hodnot lze definovat jako ( Q , F , Q f , Δ) s Q = { Bool , BList } , Q f = { BList } a Δ sestávající z pravidel

Nepravdivé → Bool ( false ) (1),
skutečný → Bool ( pravda ) (2),
nula → BList ( nula ) (3) a
nevýhody ( Bool (x 1 ), BList (x 2 )) → BList ( nevýhody (x 1 , x 2 ))       (4).

V tomto příkladu lze pravidla chápat intuitivně tak, že každému výrazu přiřazuje jeho typ způsobem zdola nahoru; např pravidlo (4) lze číst jako "termín nevýhody ( x 1 , x 2 ), má typ blist , za předpokladu, X 1 a X 2 má typ Bool a blist , resp." Přijatelný příklad běhu je

nevýhody ( nepravda , nevýhody ( pravda , nula )))
⇒ nevýhody ( nepravda , nevýhody ( pravda , BList ( nula ) ))) od (3)
⇒ nevýhody ( nepravda , nevýhody ( Bool ( pravda ), BList ( nula ) ))) podle (2)
⇒ nevýhody ( nepravda , BList ( nevýhody ( pravda , nula ))) od (4)
⇒ nevýhody ( Bool ( false ), BList ( nevýhody ( pravda , nula ))) od (1)
⇒ BList ( nevýhody ( nepravda , nevýhody ( pravda , nula )))       (4), přijato.

Srov. odvození stejného výrazu z pravidelné stromové gramatiky odpovídající automatu, ukázané na Pravidelné stromové gramatice#Příklady .

Odmítnutí příkladu běhu je

nevýhody ( nepravda , skutečný )
⇒ nevýhody ( nepravda , Bool ( pravda ) ) od (1)
⇒ nevýhody ( Bool ( false ), Bool ( pravda ) )       do (2), nepoužije se žádné další pravidlo.

Intuitivně to odpovídá výrazu cons ( false , true ), který není dobře napsaný.

Automat shora dolů přijímající násobky 3 v binární notaci

(A) (B) (C) (D)
Řetězcová
gramatická
pravidla 		Řetězcové
automatické
přechody 		Přechody stromových
automatů
Pravidla stromové gramatiky
0
1
2
3
4
5
6
S 0 → ε
S 0 → 0 S 0
S 0 → 1 S 1
S 1 → 0 S 2
S 1 → 1 S 0
S 2 → 0 S 1
S 2 → 1 S 2
 
δ ( S 0 , 0 ) = S 0
δ ( S 0 , 1 ) = S 1
δ ( S 1 , 0 ) = S 2
δ ( S 1 , 1 ) = S 0
δ ( S 2 , 0 ) = S 1
δ ( S 2 , 1 ) = S 2
S 0 ( nula ) → nula
S 0 ( 0 (x)) → 0 ( S 0 (x))
S 0 ( 1 (x)) → 1 ( S 1 (x))
S 1 ( 0 (x)) → 0 ( S 2 (x))
S 1 ( 1 (x)) → 1 ( S 0 (x))
S 2 ( 0 (x)) → 0 ( S 1 (x))
S 2 ( 1 (x)) → 1 ( S 2 (x))
S 0 → nula
S 0 → 0 ( S 0 )
S 0 → 1 ( S 1 )
S 1 → 0 ( S 2 )
S 1 → 1 ( S 0 )
S 2 → 0 ( S 1 )
S 2 → 1 ( S 2 )
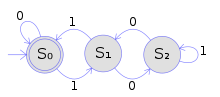
Deterministický konečný (řetězcový) automat přijímající násobky 3 v binárním zápisu

Pomocí stejného zabarvení jako výše ukazuje tento příklad, jak stromové automaty generalizují běžné řetězcové automaty. Konečný deterministický řetězcový automat zobrazený na obrázku přijímá všechny řetězce binárních číslic, které označují násobek 3. Pomocí pojmů z Deterministického konečného automatu#Formální definice je definován:

  • množina Q stavů je { S 0 , S 1 , S 2 },
  • vstupní abeceda je { 0 , 1 },
  • počáteční stav je S 0 ,
  • množina konečných stavů je { S 0 } a
  • přechody jsou uvedeny ve sloupci (B) tabulky.

V nastavení stromového automatu se vstupní abeceda změní tak, že symboly 0 a 1 jsou unární a pro listy stromů se použije nulový symbol, řekněme nula . Například binární řetězec „ 110 “ v nastavení řetězcového automatu odpovídá výrazu „ 1 ( 1 ( 0 ( nil )))“ v nastavení stromového automatu; tímto způsobem lze řetězce generalizovat na stromy nebo výrazy. Automatický konečný strom shora dolů přijímající množinu všech výrazů odpovídajících násobkům 3 v binárním řetězcovém zápisu je pak definován:

  • množina Q stavů je stále { S 0 , S 1 , S 2 },
  • seřazená vstupní abeceda je { 0 , 1 , nula }, přičemž Arity ( 0 ) = Arity ( 1 ) = 1 a Arity ( nil ) = 0, jak je vysvětleno,
  • množina počátečních stavů je { S 0 }, a
  • přechody jsou uvedeny ve sloupci (C) tabulky.

Například strom „ 1 ( 1 ( 0 ( nil )))“ je přijat následujícím spuštěním automatického stromu:

S 0 ( 1 ( 1 ( 0 ( nula ))))
⇒ 1 ( S 1 ( 1 ( 0 ( nula )))) do 2
⇒ 1 ( 1 ( S 0 ( 0 ( nula )))) do 4
⇒ 1 ( 1 ( 0 ( S 0 ( nula )))) o 1
⇒ 1 ( 1 ( 0 ( nula )))       od 0

Naproti tomu termín „ 1 ( 0 ( nil ))“ vede k následujícímu neakceptujícímu běhu automatu:

⇒ S 0 ( 1 ( 0 ( nula )))
⇒ 1 ( S 1 ( 0 ( nula )))) do 2
⇒ 1 ( 0 ( S 2 ( nula ))))       do 3, žádné další pravidlo neplatí

Protože neexistují žádné jiné počáteční stavy než S 0 pro spuštění běhu automatu, stromový automat neakceptuje výraz „ 1 ( 0 ( nil ))“.

Pro účely srovnání tabulka uvádí ve sloupci (A) a (D) pravidelnou (řetězcovou) gramatiku a pravidelnou stromovou gramatiku , přičemž každý přijímá stejný jazyk jako jeho protějšek z automatu.

Vlastnosti

Rozpoznatelnost

Pro automat zdola nahoru je přijat základní termín t (tj. Strom), pokud existuje redukce, která začíná od t a končí q ( t ), kde q je konečný stav. U automatu shora dolů je akceptován základní člen t, pokud existuje redukce, která začíná od q ( t ) a končí t , kde q je počáteční stav.

Strom jazyk L ( ) přijat , nebo uznán , u stromu automatem A je množina všech pozemních podmínkách přijatých A . Soubor základních výrazů je rozpoznatelný, pokud existuje stromový automat, který ho přijímá.

Lineární (tj. Zachování arity) stromový homomorfismus zachovává rozpoznatelnost.

Úplnost a redukce

Nedeterministický automat konečných stromů je úplný, pokud je pro každou možnou kombinaci symbolů k dispozici alespoň jedno přechodové pravidlo. Stav q je přístupný, pokud existuje základní člen t takový, že existuje snížení z t na q ( t ). NFTA je omezena, pokud jsou přístupné všechny její stavy.

Čerpací lemma

Každý dostatečně velké pozemní termín t rozpoznatelným strom jazyka L může být vertikálně tripartited tak, že libovolná opakování ( „čerpání“) na střední části udržuje výsledný výraz v L .

Pro jazyk všech konečných seznamů booleovských hodnot z výše uvedeného příkladu lze čerpat všechny výrazy nad výškovým limitem k = 2, protože musí obsahovat výskyt nevýhod . Například,

nevýhody ( nepravda , nevýhody ( pravda , nula ) ) ,
cons ( false , cons ( false , nevýhody ( pravda , nula ) ))) ,
cons ( false , cons ( false , cons ( false , nevýhody ( pravda , nula ) ))) , ...

všichni patří tomuto jazyku.

Uzavření

Třída rozpoznatelných jazyků stromů je uzavřena pod sjednocením, doplňováním a průnikem.

Myhill – Nerodeova věta

Shoda na množině všech stromů nad seřazenou abecedou F je vztah ekvivalence takový, že u 1 ≡ v 1 a ... a u n ≡ v n znamená f ( u 1 , ..., u n ) ≡ f ( v 1 , ..., v n ), pro každé f ∈ F . Je to konečný index, pokud je jeho počet tříd ekvivalence konečný.

Pro daný strom jazyka L , je shoda může být definován u ≡ L v případě, C [ u ] ∈ L ⇔ C [ V ] ∈ L pro každý kontextové C .

Myhill-Nerode teorém pro stromové automaty uvádí, že následující tři výroky jsou ekvivalentní:

  1. L je rozpoznatelný stromový jazyk
  2. L je spojení některých tříd ekvivalence shody konečného indexu
  3. vztah ≡ L je kongruence konečného indexu

Viz také

Poznámky

Reference

  • Comon, Hubert; Dauchet, Max; Gilleron, Rémi; Jacquemard, Florent; Lugiez, Denis; Löding, Christof; Tison, Sophie; Tommasi, Marc (listopad 2008). Tree Automata Techniques and Applications (PDF) . Vyvolány 11 February 2014 .
  • Hosoya, Haruo (4. listopadu 2010). Základy zpracování XML: The Tree-Automata Approach . Cambridge University Press. ISBN 978-1-139-49236-2.

externí odkazy

Implementace

  • Grappa - hodnocené a nezařazené stromové knihovny automatických knihoven (OCaml)
  • Timbuk - nástroje pro analýzu dosažitelnosti a výpočty stromových automatů (OCaml)
  • LETHAL - knihovna pro práci s automaty na konečné stromy a živé ploty (Java)
  • Strojově kontrolovaná knihovna stromových automatů (Isabelle [OCaml, SML, Haskell])
  • VATA - knihovna pro efektivní manipulaci s nedeterministickými stromovými automaty (C ++)