Trojúhelníková nerovnost - Triangle inequality

Tento článek je o základní nerovnosti . Další nerovnosti spojené s trojúhelníky viz Seznam nerovností trojúhelníků .${\ Displaystyle z \ leq x+y}$

Tři příklady nerovnosti trojúhelníku pro trojúhelníky se stranami délek x , y , z . Horní příklad ukazuje případ, kde z je mnohem menší než součet x + y ostatních dvou stran, a spodní příklad ukazuje případ, kdy strana z je jen o málo menší než x + y .

V matematiky , že trojúhelník nerovnost uvádí, že pro každý trojúhelník , součet délek libovolných dvou stran, musí být větší nebo rovna délce zbývající strany. Toto tvrzení umožňuje zahrnutí degenerovaných trojúhelníků , ale někteří autoři, zejména ti, kteří píší o elementární geometrii, tuto možnost vyloučí, čímž vynechají možnost rovnosti. Pokud x , y a z jsou délky stran trojúhelníku, přičemž žádná strana není větší než z , pak nerovnost trojúhelníku uvádí, že

${\ Displaystyle z \ leq x+y,}$

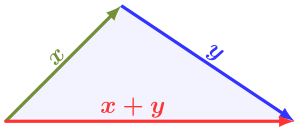
s rovností pouze v degenerovaném případě trojúhelníku s nulovou oblastí. V euklidovské geometrii a některých dalších geometriích je nerovnost trojúhelníku větou o vzdálenostech a je psána pomocí vektorů a vektorových délek ( norem ):

${\ Displaystyle \ | \ mathbf {x} +\ mathbf {y} \ | \ leq \ | \ mathbf {x} \ | +\ | \ mathbf {y} \ |,}$

kde délka z třetí strany byla nahrazena vektorovým součtem x + y . Když x a y jsou reálná čísla , lze je zobrazit jako vektory v R ¹ a nerovnost trojúhelníku vyjadřuje vztah mezi absolutními hodnotami .

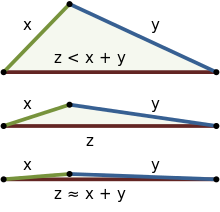
V euklidovské geometrii je u pravoúhlých trojúhelníků nerovnost trojúhelníku důsledkem Pythagorovy věty a u obecných trojúhelníků důsledkem kosinova zákona , i když to lze dokázat i bez těchto vět. Na nerovnost lze intuitivně pohlížet buď v R ^2, nebo R ³ . Obrázek vpravo ukazuje tři příklady začínající jasnou nerovností (nahoře) a blížící se rovností (dole). V euklidovském případě dochází k rovnosti pouze v případě, že trojúhelník má úhel 180 ° a dva úhly 0 ° , takže tři vrcholy jsou kolineární , jak ukazuje spodní příklad. V euklidovské geometrii je tedy nejkratší vzdálenost mezi dvěma body přímka.

Ve sférické geometrii je nejkratší vzdálenost mezi dvěma body obloukem velkého kruhu , ale nerovnost trojúhelníku platí za předpokladu, že je omezeno, že vzdálenost mezi dvěma body na kouli je délka menšího sférického čárového segmentu (tj. jeden se středovým úhlem v [0, π ] ) s těmito koncovými body.

Trojúhelník nerovnost je definování vlastnosti z norem a opatření vzdálenost . Tato vlastnost musí být stanovena jako teorém pro jakoukoli funkci navržené pro takové účely, pro každý konkrétní prostoru: například prostory, jako jsou reálná čísla , euklidovských prostorů , v L ^p prostory ( p ≥ 1 ), a vnitřní prostor produktů .

Euklidovská geometrie

Euklidova konstrukce pro důkaz nerovnosti trojúhelníku pro rovinnou geometrii.

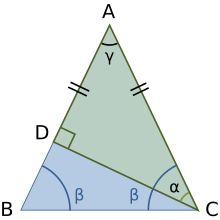
Euclid pomocí konstrukce na obrázku prokázal nerovnost trojúhelníku pro vzdálenosti v rovinné geometrii . Počínaje trojúhelníkem ABC je rovnoramenný trojúhelník zkonstruován tak, že jedna strana je považována za BC a druhá rovná noha BD podél prodloužení strany AB . Potom se argumentuje, že úhel β > α , tedy strana AD > AC . Ale AD = AB + BD = AB + BC, takže součet stran AB + BC > AC . Tento důkaz se objevuje v Euclidových prvcích , Kniha 1, Propozice 20.

Matematické vyjádření vazby na stranách trojúhelníku

Pro správný trojúhelník se nerovnost trojúhelníku, jak je uvedeno ve slovech, doslova překládá do tří nerovností (vzhledem k tomu, že správný trojúhelník má délky stran a , b , c, které jsou všechny kladné a vylučují degenerovaný případ nulové oblasti):

${\ Displaystyle a+b> c, \ quad b+c> a, \ quad c+a> b.}$

Může být ukázána stručnější forma tohoto systému nerovností

${\ Displaystyle | ab | <c <a+b.}$

Další způsob, jak to uvést, je

${\ Displaystyle \ max (a, b, c) <a+b+c- \ max (a, b, c)}$

naznačující

${\ Displaystyle 2 \ max (a, b, c) <a+b+c}$

a tedy že nejdelší délka strany je menší než semiperimetr .

Matematicky ekvivalentní formulace je, že plocha trojúhelníku se stranami a , b , c musí být skutečné číslo větší než nula. Heronův vzorec pro tuto oblast je

${\ Displaystyle {\ begin {aligned} 4 \ cdot {\ text {area}} & = {\ sqrt {(a+b+c) (-a+b+c) (a-b+c) (a+ bc)}} \\ & = {\ sqrt {-a^{4} -b^{4} -c^{4}+2a^{2} b^{2}+2a^{2} c^{ 2}+2b^{2} c^{2}}}. \ End {aligned}}}$

Pokud jde o vyjádření obou oblastí, nerovnost trojúhelníku uložená na všech stranách je ekvivalentní podmínce, že výraz pod odmocninou je skutečný a větší než nula (takže plošný výraz je skutečný a větší než nula).

Nerovnost trojúhelníku poskytuje další dvě zajímavá omezení pro trojúhelníky, jejichž strany jsou a, b, c , kde a ≥ b ≥ c a je zlatý řez , jako ${\ displaystyle \ phi}$

${\ Displaystyle 1 <{\ frac {a+c} {b}} <3}$

${\ Displaystyle 1 \ leq \ min \ left ({\ frac {a} {b}}, {\ frac {b} {c}} \ right) <\ phi.}$

Pravoúhlý trojuhelník

Rovnoměrný trojúhelník se stejnými stranami AB = AC rozdělený na dva pravé trojúhelníky výškou nakreslenou z jednoho ze dvou základních úhlů.

V případě pravoúhlých trojúhelníků se nerovnost trojúhelníků specializuje na tvrzení, že přepona je větší než na obou stranách a menší než jejich součet.

Druhá část této věty je již stanovena výše pro kteroukoli stranu libovolného trojúhelníku. První část je stanovena pomocí spodního obrázku. Na obrázku zvažte pravý trojúhelník ADC . Rovnoměrný trojúhelník ABC je konstruován se stejnými stranami AB = AC . Z postulátu trojúhelníku splňují úhly v pravoúhlém trojúhelníku ADC :

${\ Displaystyle \ alpha +\ gamma = \ pi /2 \.}$

Stejně tak v rovnoramenném trojúhelníku ABC úhly splňují:

${\ Displaystyle 2 \ beta +\ gamma = \ pi \.}$

Proto,

${\ Displaystyle \ alpha = \ pi /2- \ gamma, \ \ mathrm {while} \ \ beta = \ pi /2- \ gamma /2 \,}$

a tak zejména

${\ displaystyle \ alpha <\ beta \.}$

To znamená, že strana AD opačný úhel α je kratší než strana AB proti většímu úhlu β . Ale AB = AC . Proto:

${\ displaystyle {\ overline {\ mathrm {AC}}}> {\ overline {\ mathrm {AD}}} \.}$

Podobná konstrukce ukazuje AC > DC , která stanoví větu.

Alternativní důkaz (také založený na postulátu trojúhelníku) pokračuje zvážením tří pozic pro bod B : (i) jak je znázorněno (což má být prokázáno), nebo (ii) B shodující se s D (což by znamenalo, že rovnoramenný trojúhelník měl dvě pravé úhly jako základní úhly plus vrcholový úhel γ , což by narušilo postulát trojúhelníku ), nebo nakonec (iii) B vnitřní k pravoúhlému trojúhelníku mezi body A a D (v takovém případě úhel ABC je vnější úhel pravoúhlého trojúhelníku BDC, a proto je větší než π /2 , což znamená, že druhý základní úhel rovnoramenného trojúhelníku je také větší než π /2 a jejich součet přesahuje π v rozporu s postulátem trojúhelníku).

Tuto větu zakládající nerovnosti vyostřuje Pythagorova věta na rovnost, že čtverec délky přepony se rovná součtu čtverců ostatních dvou stran.

Příklady použití

Uvažujme trojúhelník, jehož strany jsou v aritmetickém postupu, a nechme strany a , a + d , a + 2 d . Pak to vyžaduje nerovnost trojúhelníku

${\ Displaystyle 0 <a <2a+3d}$

${\ Displaystyle 0 <a+d <2a+2d}$

${\ Displaystyle 0 <a+2d <2a+d.}$

Uspokojit všechny tyto nerovnosti vyžaduje

${\ Displaystyle a> 0 {\ text {a}}-{\ frac {a} {3}} <d <a.}$

Když je d vybráno tak, že d = a /3 , generuje pravoúhlý trojúhelník, který je vždy podobný Pythagorově trojici se stranami 3 , 4 , 5 .

Nyní zvažte trojúhelník, jehož strany jsou v geometrickém průběhu, a nechte strany a , ar , ar ² . Pak to vyžaduje nerovnost trojúhelníku

${\ displaystyle 0 <a <ar+ar^{2}}$

${\ Displaystyle 0 <ar <a+ar^{2}}$

${\ Displaystyle 0 <ar^{2} <a+ar.}$

První nerovnost vyžaduje a > 0 ; v důsledku toho může být rozdělena a eliminována. S s > 0 , prostřední nerovnost vyžaduje pouze r > 0 . Nyní zbývá první a třetí nerovnost, které je třeba uspokojit

${\ displaystyle {\ begin {aligned} r^{2}+r-1 & {}> 0 \\ r^{2} -r-1 & {} <0. \ end {aligned}}}$

První z těchto kvadratických nerovností vyžaduje, aby se r pohybovalo v oblasti za hodnotou kladného kořene kvadratické rovnice r ² + r - 1 = 0 , tj. R > φ - 1, kde φ je zlatý řez . Druhá kvadratická nerovnost vyžaduje, aby se r pohybovalo mezi 0 a kladným kořenem kvadratické rovnice r ² - r - 1 = 0 , tj. 0 < r < φ . Výsledkem kombinovaných požadavků je omezení r na rozsah

${\ Displaystyle \ varphi -1 <r <\ varphi \, {\ text {and}} a> 0.}$

Když je r společný poměr zvolen tak, že r = √ φ generuje pravoúhlý trojúhelník, který je vždy podobný Keplerovu trojúhelníku .

Zobecnění na jakýkoli polygon

Trojúhelníkovou nerovnost lze rozšířit matematickou indukcí na libovolné polygonální cesty, což ukazuje, že celková délka takové dráhy není menší než délka přímky mezi jejími koncovými body. V důsledku toho je délka jakékoli polygonové strany vždy menší než součet ostatních délkových polygonových stran.

Příklad zobecněné polygonové nerovnosti pro čtyřúhelník

Zvažte čtyřúhelník, jehož strany jsou v geometrickém průběhu, a nechte strany a , ar , ar ² , ar ³ . Pak to vyžaduje generalizovaná polygonová nerovnost

${\ Displaystyle 0 <a <ar+ar^{2}+ar^{3}}$

${\ Displaystyle 0 <ar <a+ar^{2}+ar^{3}}$

${\ Displaystyle 0 <ar^{2} <a+ar+ar^{3}}$

${\ Displaystyle 0 <ar^{3} <a+ar+ar^{2}.}$

Tyto nerovnosti pro > 0 snižují následujícímu

${\ Displaystyle r^{3}+r^{2}+r-1> 0}$

${\ Displaystyle r^{3} -r^{2} -r-1 <0.}$

Polynomy těchto dvou nerovností na levé straně mají kořeny, které jsou tribonacciho konstantou a její vzájemností. V důsledku toho je r omezeno na rozsah 1/ t < r < t, kde t je tribonacciho konstanta.

Vztah s nejkratšími cestami

Délka oblouku křivky je definována jako nejmenší horní hranice délek polygonálních aproximací.

Toto zobecnění lze použít k prokázání, že nejkratší křivka mezi dvěma body v euklidovské geometrii je přímka.

Žádná polygonální cesta mezi dvěma body není kratší než čára mezi nimi. To znamená, že žádná křivka nemůže mít délku oblouku menší než vzdálenost mezi jejími koncovými body. Podle definice je délka oblouku křivky nejmenší horní hranou délek všech polygonálních aproximací křivky. Výsledek pro polygonální cesty ukazuje, že přímka mezi koncovými body je ze všech polygonálních aproximací nejkratší. Protože délka oblouku křivky je větší nebo rovna délce každé polygonální aproximace, nemůže být samotná křivka kratší než přímka.

Konverzovat

Platí také opak věty o nerovnosti trojúhelníku: pokud jsou tři reálná čísla taková, že každé je menší než součet ostatních, pak existuje trojúhelník s těmito čísly jako délkami stran as kladnou plochou; a pokud se jedno číslo rovná součtu ostatních dvou, existuje zde degenerovaný trojúhelník (tj. s nulovou oblastí) s těmito čísly jako délkami stran.

V obou případech, pokud jsou délky stran a, b, c, můžeme se pokusit umístit trojúhelník do euklidovské roviny, jak je znázorněno na obrázku. Musíme dokázat, že existuje skutečné číslo h v souladu s hodnotami a, b, a c , v takovém případě tento trojúhelník existuje.

Trojúhelník s nadmořskou výškou h řezání základny c do d + ( c - d ) .

Podle Pythagorovy věty máme b ² = h ² + d ² a a ² = h ² + ( c - d ) ² podle obrázku vpravo. Odečtením těchto výnosů a ² - b ² = c ² - 2 cd . Tato rovnice nám umožňuje vyjádřit d pomocí stran trojúhelníku:

${\ Displaystyle d = {\ frac {-a^{2}+b^{2}+c^{2}} {2c}}.}$

Pro výšku trojúhelníku platí, že h ² = b ² - d ² . Nahrazením d vzorcem uvedeným výše máme

${\ Displaystyle h^{2} = b^{2}-\ left ({\ frac {-a^{2}+b^{2}+c^{2}} {2c}} \ right)^{ 2}.}$

Aby to splnilo skutečné číslo h , musí být nezáporné: ${\ displaystyle h^{2}}$

${\ Displaystyle b^{2}-\ left ({\ frac {-a^{2}+b^{2}+c^{2}} {2c}} \ right)^{2} \ geq 0, }$

${\ Displaystyle \ left (b-{\ frac {-a^{2}+b^{2}+c^{2}} {2c}} \ right) \ left (b+{\ frac {-a^{ 2}+b^{2}+c^{2}} {2c}} \ vpravo) \ geq 0,}$

${\ Displaystyle \ left (a^{2}-(bc)^{2}) ((b+c)^{2} -a^{2} \ right) \ geq 0,}$

${\ Displaystyle (a+bc) (a-b+c) (b+c+a) (b+ca) \ geq 0,}$

${\ Displaystyle (a+bc) (a+cb) (b+ca) \ geq 0,}$

což platí, pokud je nerovnost trojúhelníku splněna pro všechny strany. Proto existuje reálné číslo h shodné se stranami a, b, c a trojúhelník existuje. Pokud každá nerovnost trojúhelníku platí striktně , h > 0 a trojúhelník je nedegenerovaný (má kladnou oblast); ale pokud jedna z nerovností platí pro rovnost, tak h = 0, je trojúhelník degenerovaný.

Zobecnění na vyšší dimenze

Plocha trojúhelníkového obličeje čtyřstěnu je menší nebo rovna součtu ploch ostatních tří trojúhelníkových ploch. Obecněji, v euklidovském prostoru hyperarea z ( n - 1) - aspekt o o n - simplex (tj trojúhelník ( n = 2 ), čtyřstěn ( n = 3 ), pentatope ( n = 4 ), atd.), Je menší nebo roven součtu hyperreaktů ostatních n fazet. Stejně jako se nerovnost trojúhelníku zobecňuje na nerovnost polygonu - viz výše - nerovnost pro simplex jakékoli dimenze generalizuje na polytop jakékoli dimenze: hyperprostor jakéhokoli aspektu polytopu je menší nebo roven součtu hyperploch zbývající fasety.

Všimněte si, že nerovnost trojúhelníku neznamená vždy čtyřstěnnou nerovnost v následujícím smyslu. Předpokládejme, že existují čtyři body a že vzdálenosti mezi nimi jsou AB = BC = CA = 7 a AZ = BZ = CZ = 4 . Každý triplet těchto bodů splňuje nerovnost trojúhelníku, ale ukazuje se, že čtyři body nemohou být vrcholy čtyřstěnu, v tomto případě s jedním 7-7-7 rovnostranným trojúhelníkem a třemi 7-4-4 rovnoramennými trojúhelníky jako plochami. Víme to, protože čtyřstěnná nerovnost není splněna: plocha trojúhelníku ABC by byla přibližně 21,22 podle Heronova vzorce , a to není menší než součet ploch dalších tří trojúhelníků, které jsou podle Heronova vzorce přibližně po 6,78 .

Normovaný vektorový prostor

Trojúhelníková nerovnost pro normy vektorů.

V normovaném vektorovém prostoru V je jednou z definujících vlastností normy trojúhelníková nerovnost:

${\ Displaystyle \ | x+y \ | \ leq \ | x \ |+\ | y \ | \ quad \ forall \, x, y \ v V}$

to znamená, že norma součtu dvou vektorů je nanejvýš tak velká jako součet norem těchto dvou vektorů. Toto je také označováno jako subaditivita . Aby se jakákoli navrhovaná funkce chovala jako norma, musí tento požadavek splňovat. Pokud je normovaný prostor euklidovský nebo obecněji konvexní , pak právě tehdy, když je trojúhelník tvořený x , y a x + y , degenerovaný, to znamená, že x a y jsou na stejném paprsku, tj. x = 0 nebo y = 0 , nebo x = α y pro některé α > 0 . Tato vlastnost charakterizuje přísně konvexní normované prostory, jako jsou ℓ _p mezery s 1 < p <∞ . Existují však normované prostory, ve kterých to není pravda. Zvažte například rovinu s normou ℓ ₁ ( vzdálenost Manhattanu ) a označte x = (1, 0) a y = (0, 1) . Potom trojúhelník tvořený x , y a x + y není degenerovaný, ale ${\ Displaystyle \ | x+y \ | = \ | x \ |+\ | y \ |}$

${\ Displaystyle \ | x+y \ | = \ | (1,1) \ | = | 1 |+| 1 | = 2 = \ | x \ |+\ | y \ |.}$

Příklady norem

• Absolutní hodnota jako norma pro skutečnou linku . Aby byla nerovnost trojúhelníku normou, vyžaduje, aby absolutní hodnota splňovala všechna reálná čísla x a y :
  $${\ Displaystyle | x+y | \ leq | x |+| y |,}$$

  
  což dělá.

Důkaz:

${\ Displaystyle -\ left \ vert x \ right \ vert \ leq x \ leq \ left \ vert x \ right \ vert}$

${\ Displaystyle -\ left \ vert y \ right \ vert \ leq y \ leq \ left \ vert y \ right \ vert}$

Po přidání,

${\ Displaystyle -(\ left \ vert x \ right \ vert +\ left \ vert y \ right \ vert) \ leq x +y \ leq \ left \ vert x \ right \ vert +\ left \ vert y \ right \ vert}$

Využijte toho, že (s b nahrazeno x + y a a za ) máme ${\ Displaystyle \ left \ vert b \ right \ vert \ leq a \ Leftrightarrow -a \ leq b \ leq a}$${\ Displaystyle \ left \ vert x \ right \ vert +\ left \ vert y \ right \ vert}$

${\ Displaystyle | x+y | \ leq | x |+| y |}$

Trojúhelníková nerovnost je užitečná v matematické analýze pro určení nejlepšího horního odhadu velikosti součtu dvou čísel z hlediska velikostí jednotlivých čísel.

Existuje také nižší odhad, který lze nalézt pomocí nerovnosti opačného trojúhelníku, která uvádí, že pro všechna reálná čísla x a y :

${\ Displaystyle | xy | \ geq {\ biggl |} | x |-| y | {\ biggr |}.}$

• Vnitřní produkt jako norma ve vnitřním produktovém prostoru . Pokud norma vychází z vnitřního součinu (jako je tomu v případě euklidovských prostorů), pak nerovnost trojúhelníku vyplývá z Cauchy -Schwarzovy nerovnosti následovně: Dané vektory a , a označující vnitřní součin jako :${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle \ langle x, y \ rangle}$

${\ Displaystyle \ | x+y \ |^{2}}$	${\ Displaystyle = \ langle x+y, x+y \ rangle}$
	${\ Displaystyle = \ | x \ |^{2} +\ langle x, y \ rangle +\ langle y, x \ rangle +\ | y \ |^{2}}$
	${\ Displaystyle \ leq \ | x \ |^{2} +2 | \ langle x, y \ rangle |+\ | y \ |^{2}}$
	${\ Displaystyle \ leq \ | x \ |^{2} +2 \ | x \ | \ | y \ |+\ | y \ |^{2}}$ (podle Cauchy -Schwarzovy nerovnosti)
	${\ Displaystyle = \ left (\ | x \ |+\ | y \ | \ right)^{2}}$.

Cauchyho -Schwarzova nerovnost se mění v rovnost právě tehdy, když x a y jsou lineárně závislé. Nerovnost se změní na rovnost pro lineárně závislou a právě tehdy, když jeden z vektorů x nebo y je nezáporným skalárem druhého. ${\ Displaystyle \ langle x, y \ rangle +\ langle y, x \ rangle \ leq 2 \ left | \ left \ langle x, y \ right \ rangle \ right |}$${\ displaystyle x}$${\ displaystyle y}$

Vezmeme -li druhou odmocninu konečného výsledku, dostaneme nerovnost trojúhelníku.

• p -norm: běžně používanou normou jep-norm:
  $${\ Displaystyle \ | x \ | _ {p} = \ left (\ sum _ {i = 1}^{n} | x_ {i} |^{p} \ right)^{1/p} \,}$$

  
  kde x _i jsou komponenty vektoru x . Pro p = 2 se p -norm stane euklidovskou normou :
  $${\ Displaystyle \ | x \ | _ {2} = \ left (\ sum _ {i = 1}^{n} | x_ {i} |^{2} \ right)^{1/2} = \ left (\ sum _ {i = 1}^{n} x_ {i}^{2} \ vpravo)^{1/2} \,}$$

  
  což je Pythagorova věta v n -dimenzích, velmi zvláštní případ odpovídající vnitřní produktové normě. S výjimkou případu p = 2, je p -norm je není vnitřní produkt normou, protože nesplňuje zákona rovnoběžníku . Trojúhelníková nerovnost pro obecné hodnoty p se nazývá Minkowského nerovnost . Má formu:
  $${\ Displaystyle \ | x+y \ | _ {p} \ leq \ | x \ | _ {p}+\ | y \ | _ {p} \.}$$

  

Metrický prostor

V metrickém prostoru M s metrickým d je nerovnost trojúhelníku požadavkem na vzdálenost :

${\ Displaystyle d (x, \ z) \ leq d (x, \ y)+d (y, \ z) \,}$

pro všechny x , y , z, v M . To znamená, že vzdálenost od x do z je maximálně tak velká jako součet vzdálenosti od x do y a vzdálenosti od y do z .

Trojúhelníková nerovnost je zodpovědná za většinu zajímavé struktury v metrickém prostoru, konkrétně za konvergenci. Důvodem je, že zbývající požadavky na metriku jsou ve srovnání spíše zjednodušující. Například skutečnost, že jakákoli konvergentní sekvence v metrickém prostoru je Cauchyova posloupnost, je přímým důsledkem nerovnosti trojúhelníku, protože pokud zvolíme libovolné x _n a x _m takové, že d ( x _n , x ) < ε /2 a d ( x _m , x ) < ε /2 , kde ε > 0 je dáno a libovolné (jako v definici limitu v metrickém prostoru), pak trojúhelníkovou nerovností, d ( x _n , x _m ) ≤ d ( x _n , x ) + d ( x _m , x ) < ε /2 + ε /2 = ε , takže sekvence { x _n } je podle definice Cauchyova sekvence.

Tato verze nerovnosti trojúhelníku se snižuje na tu uvedenou výše v případě normovaných vektorových prostorů, kde je metrika indukována pomocí d ( x , y ) ≔ ‖ x - y ‖ , přičemž x - y je vektor směřující z bodu y do x .

Reverzní nerovnost trojúhelníku

Reverzní trojúhelník nerovnost je základní důsledek nerovnosti trojúhelníku, který dává dolní hranice namísto horní hranice. Pro rovinnou geometrii platí:

Jakákoli strana trojúhelníku je větší nebo rovna rozdílu mezi ostatními dvěma stranami .

V případě normovaného vektorového prostoru je příkaz:

${\ Displaystyle {\ bigg |} \ | x \ |-\ | y \ | {\ bigg |} \ leq \ | xy \ |,}$

nebo pro metrické prostory, | d ( y , x ) - d ( x , z ) | ≤ d ( y , z ) . To znamená, že norma i funkce vzdálenosti jsou Lipschitzovy spojité s Lipschitzovou konstantou 1 , a proto jsou zejména rovnoměrně spojité . ${\ displaystyle \ | \ cdot \ |}$${\ Displaystyle d (x, \ cdot)}$

Důkaz pro reverzní trojúhelník používá nerovnost pravidelného trojúhelníku a : ${\ Displaystyle \ | yx \ | = \ | {-} 1 (xy) \ | = | {-} 1 | \ cdot \ | xy \ | = \ | xy \ |}$

${\ Displaystyle \ | x \ | = \ | (xy)+y \ | \ leq \ | xy \ |+\ | y \ | \ Rightarrow \ | x \ |-\ | y \ | \ leq \ | xy \ |,}$

${\ Displaystyle \ | y \ | = \ | (yx)+x \ | \ leq \ | yx \ |+\ | x \ | \ Rightarrow \ | x \ | -\ | y \ | \ geq -\ | xy \ |,}$

Kombinací těchto dvou prohlášení získáte:

${\ Displaystyle-\ | xy \ | \ leq \ | x \ |-\ | y \ | \ leq \ | xy \ | \ Rightarrow {\ bigg |} \ | x \ |-\ | y \ | {\ bigg |} \ leq \ | xy \ |.}$

Zvrat v prostoru Minkowski

Minkowski prostor metrika není pozitivně definitní, což znamená, že mohou mít buď znak nebo zmizí, a to i v případě, že vektor x je nenulový. Navíc, pokud x a y jsou oba časové vektory ležící v budoucím světelném kuželu, nerovnost trojúhelníku se obrátí: ${\ Displaystyle \ eta _ {\ mu \ nu}}$${\ Displaystyle \ | x \ |^{2} = \ eta _ {\ mu \ nu} x^{\ mu} x^{\ nu}}$

${\ Displaystyle \ | x+y \ | \ geq \ | x \ |+\ | y \ |.}$

Fyzickým příkladem této nerovnosti je paradox dvojčat ve speciální relativitě . Stejná obrácená forma nerovnosti platí, pokud oba vektory leží v minulém světelném kuželu a pokud jeden nebo oba jsou nulové vektory. Výsledek platí v rozměrech n + 1 pro libovolné n ≥ 1. Pokud je rovina definovaná x a y prostorová (a tedy euklidovský podprostor), pak platí obvyklá trojúhelníková nerovnost.

Viz také

• Subaditivita
• Minkowského nerovnost
• Ptolemaiova nerovnost

Poznámky

Reference

• Pedoe, Daniel (1988). Geometrie: Komplexní kurz . Dover. ISBN 0-486-65812-0..
• Rudin, Walter (1976). Zásady matematické analýzy . New York: McGraw-Hill . ISBN 0-07-054235-X..

externí odkazy

• Nerovnost trojúhelníků na ProofWiki