Multilaterace skutečného rozsahu - True-range multilateration
Multilaterace v reálném rozsahu je metoda ke stanovení polohy pohyblivého vozidla nebo stacionárního bodu v prostoru pomocí několika rozsahů (vzdáleností) mezi vozidlem/bodem a několika prostorově oddělenými známými místy (často nazývanými „stanice“). Název je odvozen od trilaterace , v geometrické problém určení neznámé polohy do roviny na základě vzdálenosti dvou dalších známých vrcholy jednoho trojúhelníku (délka obou stranách ). Multilaterace v reálném rozsahu je jak matematické téma, tak aplikovaná technika používaná v několika oblastech. Praktickou aplikací zahrnující pevné umístění je trilaterační metoda průzkumu . Aplikace zahrnující polohu vozidla se nazývají navigace, když jsou palubní osoby/zařízení informovány o jeho poloze, a nazývají se dohledové, když jsou subjekty mimo vozidlo informovány o poloze vozidla.
K vyhledání třetího bodu v dvourozměrném karteziánském prostoru (rovině) lze použít dva šikmé rozsahy ze dvou známých míst, což je často používaná technika (např. Při průzkumu). Podobně lze k nalezení bodu na kouli použít dva sférické rozsahy , což je základní koncept starověké disciplíny nebeské navigace - nazývané problém výškového zachycení . Kromě toho, pokud je k dispozici více než minimální počet rozsahů, je vhodné je také použít. Tento článek řeší obecný problém určování polohy pomocí více rozsahů.
Ve dvojrozměrné geometrii je známo, že pokud bod leží na dvou kruzích, pak středy kruhů a dva poloměry poskytují dostatečné informace pro zúžení možných míst až na dvě-z nichž jedna je požadovaným řešením a druhá je nejednoznačné řešení. Další informace často zužují možnosti až na jedinečné místo. V trojrozměrné geometrii, když je známo, že bod leží na plochách tří koulí, pak středy tří koulí spolu s jejich poloměry také poskytují dostatečné informace pro zúžení možných míst až na více než dvě (pokud centra leží na přímce).
Multilateraci skutečného rozsahu lze postavit do kontrastu s častěji se vyskytující ( pseudorange ) multilaterací , která využívá rozdíly v rozsahu k nalezení (obvykle pohyblivého) bodu. Multilaterace pseudorozsahu je téměř vždy implementována měřením časů příjezdu (TOA) energetických vln. Multilateraci skutečného rozsahu lze také postavit do kontrastu s triangulací , která zahrnuje měření úhlů .
Pro podobné koncepty se používá více, někdy se překrývajících a konfliktních termínů - např. Pro letecké systémy využívající jak skutečná rozmezí, tak pseudo rozsahy byla použita multilaterace bez úprav. Navíc různé oblasti úsilí mohou používat různé termíny. V geometrii je trilaterace definována jako proces určování absolutních nebo relativních poloh bodů měřením vzdáleností pomocí geometrie kruhů , koulí nebo trojúhelníků . V geodézii je specifickou technikou trilaterace . Termín multilaterace skutečného rozsahu je přesný, obecný a jednoznačný. Autoři pro tento koncept také použili termíny range-range a rho-rho multilateration.
Problémy s implementací
Navigační a sledovací systémy obvykle zahrnují vozidla a vyžadují, aby vládní entita nebo jiná organizace rozmístila více stanic, které využívají formu radiových technologií (tj. Využívají elektromagnetické vlny). V následující tabulce jsou uvedeny výhody a nevýhody použití multilaterace skutečného rozsahu pro takový systém.
| Výhody | Nevýhody |
|---|---|
| Umístění stanic je flexibilní; mohou být umístěny centrálně nebo periferně | Uživatel je často povinen mít vysílač i přijímač |
| Přesnost pomalu klesá se vzdáleností od staničního klastru | Přesnost kooperativního systému je citlivá na chybu otáčení zařízení |
| Vyžaduje o jednu stanici méně než vícenásobný systém pseudo rozsahu | Nelze použít pro utajené sledování |
| Synchronizace stanice není náročná (na základě rychlosti bodu zájmu a může být řešena mrtvým zúčtováním ) | Nespolupracující dohled zahrnuje ztráty dráhy do čtvrté mocniny vzdálenosti |
Multilaterace skutečného rozsahu je často v kontrastu s multilaterací (pseudo rozsah), protože oba vyžadují formu uživatelských rozsahů pro více stanic. Složitost a náklady na vybavení uživatelů jsou pravděpodobně nejdůležitějším faktorem omezujícím používání multilaterace skutečného dosahu pro navigaci a sledování vozidel. Některá použití nejsou původním účelem nasazení systému - např. Navigace letadel DME/DME.
Získání rozsahů
Pro podobné rozsahy a chyby měření navigační a sledovací systém založený na multilateraci skutečného rozsahu poskytuje službu výrazně větší 2-D oblasti nebo 3-D objemu než systémy založené na multilateraci pseudo rozsahu . Měření skutečných rozsahů je však často obtížnější nebo nákladnější než měření pseudo rozsahů. Pro vzdálenosti do několika mil a pevná místa lze skutečný dosah měřit ručně. Provádí se to při geodetickém průzkumu již několik tisíc let - např. Pomocí lan a řetězů.
Pro delší vzdálenosti a/nebo jedoucí vozidla je obecně zapotřebí radio/radarový systém. Tato technologie byla poprvé vyvinuta kolem roku 1940 ve spojení s radarem. Od té doby se používají tři metody:
- Obousměrné měření dosahu, jedna strana aktivní-Jedná se o metodu používanou tradičními radary (někdy nazývanými primární radary) k určení dosahu nespolupracujícího cíle a nyní ji používají laserové dálkoměry . Jeho hlavní omezení spočívá v tom, že: (a) se cíl neidentifikuje a v situaci s více cíli může dojít k nesprávnému přiřazení výnosu; (b) zpětný signál je zeslaben (vzhledem k vysílanému signálu) čtvrtým výkonem rozsahu stanice vozidla (tedy pro vzdálenosti desítek mil a více stanice obecně vyžadují vysílače s vysokým výkonem a/nebo velké/citlivé antény); a c) mnoho systémů využívá šíření přímé viditelnosti, které omezuje jejich dosah na méně než 20 mil, když jsou obě strany v podobných výškách nad hladinou moře.
- Obousměrné měření dosahu, obě strany aktivní-Tato metoda byla údajně poprvé použita pro navigaci naváděcím systémem letadel Y-Gerät, který v roce 1941 nasadila Luftwaffe. Nyní se globálně používá v řízení letového provozu - např. Sekundární radarové sledování a navigace DME/DME. Vyžaduje, aby obě strany měly vysílače i přijímače, a může vyžadovat řešení problémů s rušením.
- Jednosměrné měření dosahu- doba letu (TOF) elektromagnetické energie mezi více stanicemi a vozidlem se měří na základě přenosu jednou stranou a příjmu druhou. Toto je nejnovější metoda a byla umožněna vývojem atomových hodin; vyžaduje, aby vozidlo (uživatel) a stanice měly synchronizované hodiny. To bylo úspěšně prokázáno s Loran-C a GPS.
Metody řešení
Algoritmy multilaterace skutečného rozsahu lze rozdělit na základě (a) dimenze problémového prostoru (obecně dvou nebo tří), (b) geometrie problémového prostoru (obecně karteziánského nebo sférického) a (c) přítomnosti nadbytečných měření (více než problémového prostoru) dimenze).
Dvě karteziánské dimenze, dva měřené šikmé rozsahy (trilaterace)
Analytické řešení je pravděpodobně známé více než 1 000 let a je uvedeno v několika textech. Navíc lze snadno přizpůsobit algoritmy pro trojrozměrný karteziánský prostor.
Nejjednodušší algoritmus využívá analytickou geometrii a souřadnicový rámec založený na stanici. Zvažte tedy středy kruhů (nebo stanice) C1 a C2 na obr. 1, které mají známé souřadnice (např. Již byly prozkoumány), a jejichž rozdělení je tedy známé. Obrázek 'stránka' obsahuje C1 a C2 . Pokud je třetí „bod zájmu“ P (např. Vozidlo nebo jiný bod, který má být zkoumán) v neznámém bodě , pak Pythagorova věta přináší
Tím pádem,
-
( 1 )
-
I když existuje mnoho vylepšení, rovnice 1 je tím nejzásadnějším multilateračním vztahem skutečného rozsahu. Navigace DME/DME letadla a trilaterační metoda průzkumu jsou příklady její aplikace. Během druhé světové války hoboj a během korejské války SHORAN používal stejný princip k navádění letadel na základě naměřených vzdáleností do dvou pozemních stanic. SHORAN byl později použit pro průzkum ropy na moři a pro letecký průzkum. Letecký průzkumný systém Australian Aerodist využíval 2-D karteziánskou multilateraci skutečného dosahu. Tento 2-D scénář je dostatečně důležitý, že termín trilaterace se často používá pro všechny aplikace zahrnující známou základní linii a dvě měření rozsahu.
Základní linie obsahující středy kruhů je linie symetrie. Správná a nejednoznačná řešení jsou kolmá a stejně vzdálená (na opačných stranách) základní linie. Nejednoznačné řešení je obvykle snadno identifikovatelné. Například pokud P je vozidlo, jakýkoli pohyb směrem k základní linii nebo od ní bude opačný než u nejednoznačného řešení; stačí tedy hrubé měření směru jízdy vozidla. Druhý příklad: inspektoři dobře vědí, na které straně základní linie leží P. Třetí příklad: v aplikacích, kde P je letadlo a C1 a C2 jsou na zemi, je nejednoznačné řešení obvykle pod zemí.
V případě potřeby lze vnitřní úhly trojúhelníku C1-C2-P zjistit pomocí trigonometrického zákona kosinů . V případě potřeby mohou být souřadnice P vyjádřeny ve druhém, známějším souřadnicovém systému-např. Systému Universal Transverse Mercator (UTM) -za předpokladu, že souřadnice C1 a C2 jsou v tomto druhém systému známy. Oba se často provádějí při průzkumu, když je použita trilaterační metoda. Jakmile jsou souřadnice P stanoveny, čáry C1-P a C2-P lze použít jako nové základní linie a prozkoumat další body. Velké oblasti nebo vzdálenosti lze tedy zkoumat na základě několika menších trojúhelníků - nazývaných traverz .
Implicitně předpoklad pro výše uvedené rovnici je to pravda, je, že a týkají stejné poloze P . Když P je vozidlo, pak obvykle a musí být měřeno v toleranci synchronizace, která závisí na rychlosti vozidla a dovolené chybě polohy vozidla. Alternativně může být účtován pohyb vozidla mezi měřeními dosahu, často mrtvým počítáním.
Je také možné goniometrické řešení (případ ze strany na straně). Možné je také řešení využívající grafiku. Grafické řešení se někdy používá při navigaci v reálném čase jako překrytí na mapě.
Tři kartézské rozměry, tři měřené šikmé rozsahy
Existuje několik algoritmů, které řeší problém multilaterace 3-D karteziánského skutečného rozsahu přímo (tj. V uzavřené formě)-např. Fang. Kromě toho lze přijmout algoritmy uzavřené formy vyvinuté pro multilateraci pseudorozsahu . Bancroftův algoritmus (přizpůsobený) využívá vektory, což je v některých situacích výhodou.
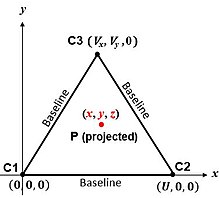
Nejjednodušší algoritmus odpovídá středům koulí na obr. 2. „Stránka“ obrázku je rovina obsahující C1 , C2 a C3 . Jestliže P je 'bod zájmu' (např. Vozidlo) v , pak Pythagorova věta poskytuje šikmé rozsahy mezi P a středy koulí:
Necháme tedy souřadnice P :
-
( 2 )
-
Rovina obsahující středy koulí je rovinou symetrie. Správná a nejednoznačná řešení jsou k němu kolmá a stejně vzdálená, na opačných stranách.
Mnoho aplikací 3-D multilaterace se skutečným dosahem zahrnuje krátké vzdálenosti-např. Přesná výroba. Integrace měření dosahu ze tří nebo více radarů (např. FAA ERAM ) je aplikace pro 3D sledování letadel. 3-D multilaterace skutečného dosahu byla experimentálně použita se satelity GPS pro navigaci letadel. Požadavek, aby letadlo bylo vybaveno atomovými hodinami, vylučuje jeho obecné použití. Pomoc s hodinami přijímače GPS je však oblastí aktivního výzkumu, včetně pomoci přes síť. Závěry se tedy mohou změnit. Multilaterace 3-D skutečného dosahu byla vyhodnocena Mezinárodní organizací pro civilní letectví jako přistávací systém letadla, ale byla shledána efektivnější jiná technika. Přesné měření výšky letadla během přiblížení a přistání vyžaduje mnoho pozemních stanic podél dráhy letu.
Dva sférické rozměry, dva nebo více měřených sférických rozsahů
Jedná se o klasický nebeský (nebo astronomický) navigační problém, nazývaný problém výškového zachycení (obr. 3). Je to sférický geometrický ekvivalent trilaterační metody průzkumu (i když zahrnuté vzdálenosti jsou obecně mnohem větší). Řešení na moři (nemusí nutně zahrnovat slunce a měsíc) umožnil námořní chronometr (zaveden v roce 1761) a objev „linie polohy“ (LOP) v roce 1837. Metoda řešení je nyní nejvíce vyučována na univerzitách ( např. US Naval Academy) využívá sférickou trigonometrii k řešení šikmého sférického trojúhelníku na základě sextantních měření „nadmořské výšky“ dvou nebeských těles. Tento problém lze také vyřešit pomocí vektorové analýzy. Historicky byly použity grafické techniky - např. Interceptová metoda . Ty mohou pojmout více než dvě měřené „nadmořské výšky“. Vzhledem k obtížnosti provádění měření na moři se často doporučuje 3 až 5 „nadmořských výšek“.
Protože je Země lépe modelována jako elipsoid revoluce než sféra, lze v moderních implementacích použít iterační techniky. V letadlech a raketách s vysokou nadmořskou výškou je nebeský navigační subsystém často integrován se setrvačným navigačním subsystémem pro provádění automatické navigace-např. US Air Force SR-71 Blackbird a B-2 Spirit .
Přestože je Loran-C zamýšlen jako „sférický“ multilaterační systém pseudo rozsahu, byl také používán jako „sférický“ multilaterační systém se skutečným dosahem dobře vybavenými uživateli (např. Kanadská hydrografická služba). To umožnilo výrazně rozšířit oblast pokrytí trojice stanic Loran-C (např. Zdvojnásobit nebo ztrojnásobit) a snížit minimální počet dostupných vysílačů ze tří na dva. V moderním letectví se častěji měří spíše šikmé než sférické rozsahy; když je však známa výška letadla, šikmé rozsahy jsou snadno převedeny na sférické rozsahy.
Měření nadbytečného rozsahu
Když je k dispozici více měření dosahu, než jsou problémové rozměry, a to buď ze stejných stanic C1 a C2 (nebo C1 , C2 a C3 ), nebo z dalších stanic, přinášejí se alespoň tyto výhody:
- „Špatná“ měření lze identifikovat a odmítnout
- Nejednoznačná řešení lze identifikovat automaticky (tj. Bez lidské účasti) - vyžaduje další stanici
- Chyby v „dobrých“ měřeních lze zprůměrovat a snížit tak jejich účinek.
Iterativní Gaussův-Newtonův algoritmus pro řešení problémů s nelineárními nejmenšími čtverci (NLLS) je obecně preferován tam, kde je více „dobrých“ měření, než je nutné minimum. Důležitou výhodou Gauss-Newtonovy metody oproti mnoha algoritmům uzavřené formy je to, že s chybami rozsahu zachází lineárně, což je často jejich povahou, čímž se snižuje průměr chyb rozsahu pomocí průměrování. Gauss -Newtonovu metodu lze také použít s minimálním počtem měřených rozsahů. Protože je to iterativní, Gaussova -Newtonova metoda vyžaduje počáteční odhad řešení.
V 3-D karteziánském prostoru čtvrtá koule eliminuje nejednoznačné řešení, ke kterému dochází u tří rozsahů, za předpokladu, že její střed není souběžný s prvními třemi. Ve 2-D karteziánském nebo sférickém prostoru třetí kruh eliminuje nejednoznačné řešení, ke kterému dochází u dvou rozsahů, za předpokladu, že jeho střed není nelineární s prvními dvěma.
Jednorázová aplikace versus opakovaná aplikace
Tento článek do značné míry popisuje „jednorázovou“ aplikaci multilaterační techniky skutečného rozsahu, což je nejzákladnější použití této techniky. S odkazem na obr. 1 je charakteristika „jednorázových“ situací v tom, že bod P a alespoň jeden z C1 a C2 se mění z jedné aplikace multilaterační techniky skutečného rozsahu na další. To je vhodné pro geodetické, nebeské navigace využívající manuální pozorování a některé letecké DME/DME navigace.
V jiných situacích se však multilaterační technika skutečného rozsahu aplikuje opakovaně (v podstatě nepřetržitě). V těchto situacích C1 a C2 (a možná Cn, n = 3,4, ... ) zůstávají konstantní a P je stejné vozidlo. Příklady aplikací (a vybrané intervaly mezi měřeními) jsou: sledování více radarových letadel (5 a 12 sekund, v závislosti na dosahu pokrytí radarem), letecké průzkumy, navigace Loran-C s vysoce přesnými hodinami uživatele (zhruba 0,1 sekundy) a některé navigace DME/DME letadla (zhruba 0,1 sekundy). Obecně platí, že implementace pro opakované použití: (a) využívají algoritmus „trackeru“ (navíc k algoritmu řešení multilateračního řešení), který umožňuje porovnávat a určitým způsobem naměřené hodnoty shromažďovat v různých časech; a (b) používají iterační algoritmus řešení, protože (bl) připouštějí různý počet měření (včetně nadbytečných měření) a (b2) mají inherentně počáteční odhad při každém vyvolání algoritmu řešení.
Hybridní multilaterační systémy
Možné jsou také hybridní multilaterační systémy - tedy systémy, které nejsou systémy se skutečným dosahem ani s pseudorozsahem. Například na obr. 1, pokud jsou středy kruhů posunuty doleva tak, že C1 je na a C2 je v, pak bod zájmu P je na
Tato forma řešení výslovně závisí na součtu a rozdílu a nevyžaduje „řetězení“ od -rozlišení do -rozlišení. Mohl by být implementován jako skutečný vícevrstevný systém měřením a .
Mohl by však být také implementován jako hybridní multilaterační systém měřením a používáním různých zařízení - např. Pro sledování multistatickým radarem s jedním vysílačem a dvěma přijímači (spíše než dvěma monostatickými radary ). Vyloučení jednoho vysílače je výhodou, ale existuje vyrovnávací „cena“: tolerance synchronizace pro dvě stanice se stává závislou na rychlosti šíření (obvykle na rychlosti světla), nikoli na rychlosti bodu P , aby bylo možné přesně měřit oba .
I když nejsou hybridní multilaterační systémy implementovány provozně, byly zkoumány pro sledování letadel v blízkosti letišť a jako záložní navigační systém GPS pro letectví.
Předběžné a konečné výpočty
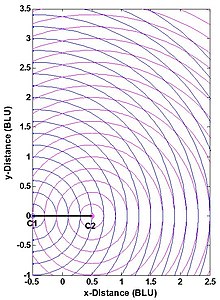
Přesnost polohy multilateračního systému se skutečným rozsahem - např. Přesnost souřadnic bodu P na obr. 1 - závisí na dvou faktorech: (1) přesnost měření rozsahu a (2) geometrický vztah P k systému stanice C1 a C2 . To lze pochopit z obr. 4. Obě stanice jsou zobrazeny jako tečky a BLU označuje základní jednotky. (Vzor měření je symetrický jak k základní linii, tak k kolmému půlící čáře základní linie, a je na obrázku zkrácen.) Jak se běžně dělá, chyby měření jednotlivých rozsahů se považují za nezávislé na rozsahu, statisticky nezávislé a identicky distribuované. Tento rozumný předpoklad odděluje účinky geometrie uživatelsky stanice a měřicí rozsah chyby na chyby v vypočtených souřadnic P . Zde je geometrie měření jednoduše úhel, pod kterým se kříží dvě kružnice-nebo ekvivalentně úhel mezi přímkami P-C1 a P-C2 . Když bod P- není na kružnici, chyba v jeho poloze je přibližně úměrná oblasti ohraničené nejbližšími dvěma modrými a nejbližšími dvěma purpurovými kruhy.
Bez nadbytečných měření nemůže být multilaterační systém se skutečným rozsahem přesnější než měření rozsahu, ale může být podstatně méně přesný, pokud není správně zvolena geometrie měření. V důsledku toho některé aplikace umístit omezení na umístění bodu P . V případě 2-D karteziánské (trilaterační) situace mají tato omezení jednu ze dvou ekvivalentních forem:
- Přípustný vnitřní úhel v bodě P mezi přímkami P-C1 a P-C2 : Ideální je pravý úhel, ke kterému dochází ve vzdálenosti od základní linie o polovinu nebo méně délky základní linie; mohou být specifikovány maximální dovolené odchylky od ideálních 90 stupňů.
- Horizontální ředění přesnosti (HDOP), které znásobuje chybu rozsahu při určování chyby polohy: Pro dva rozměry je ideální (minimální) HDOP druhá odmocnina 2 ( ), ke které dochází, když úhel mezi P-C1 a P -C2 je 90 stupňů; může být uvedena maximální povolená hodnota HDOP. (Zde jsou stejné HDOP jednoduše místem bodů na obr. 4 se stejným úhlem křížení.)
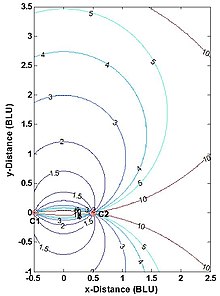
Plánování víceúrovňového navigačního nebo sledovacího systému se skutečným dosahem často zahrnuje analýzu přesnosti (DOP) s cílem informovat o rozhodování o počtu a umístění stanic a servisní oblasti systému (dvě dimenze) nebo objemu služby (tři dimenze). Obr. 5 ukazuje horizontální DOP (HDOP) pro 2-D, dvoustanový multilaterační systém se skutečným dosahem. HDOP je nekonečný podél základní linie a jejích rozšíření, protože ve skutečnosti je měřena pouze jedna ze dvou dimenzí. Uživatel takového systému by měl být zhruba soustředěný na základní linii a v rozsahu pásma závislém na aplikaci. Například pro opravy navigace DME/DME letadlem je maximální HDOP povolený americkou FAA dvojnásobkem minimální možné hodnoty nebo 2,828, což omezuje maximální rozsah použití (k němuž dochází podél základní přímky) na 1,866násobek základní délky . (Rovina obsahující dvě pozemní stanice DME a letadlo není striktně horizontální, ale obvykle je téměř taková.) Podobně geodeti vyberou bod P na obr. 1 tak, aby C1-C2-P zhruba tvořil rovnostranný trojúhelník (kde HDOP = 1,633 ).
Chyby v trilateračních průzkumech jsou diskutovány v několika dokumentech. Obecně je kladen důraz na účinky chyb měření rozsahu, nikoli na účinky numerických chyb algoritmu.
Ukázkové aplikace
- Land zaměřování pomocí metody trilateration
- Letecké průzkumy
- Průzkum námořní archeologie
- Navigace letadla DME/DME RNAV
- Integrace více radarů (např. FAA ERAM )
- Nebeská navigace pomocí metody zachycení nadmořské výšky
- Metoda interceptu - Grafické řešení problému s výškovým odposlechem
- Kalibrace laserových interferometrů
- SHORAN , Hoboj , Gee-H- Systémy navádění letadel vyvinuté pro „slepé“ bombardování
- JTIDS ( Joint Tactical Information Distribution System ) -systém USA/NATO, který (kromě jiných schopností) lokalizuje účastníky v síti pomocí mezistupňových rozsahů
- USAF SR-71 Blackbird -používá astroinerciální navigaci
- Letadlo USAF B-2 Spirit -využívá astroinerciální navigaci
Viz také
- Problém geometrie vzdálenosti , podobná technika aplikovaná na molekuly
- Nebeská navigace - starověká technika navigace založená na nebeských tělech
- Zařízení pro měření vzdálenosti (DME) - Systém používaný k měření vzdálenosti mezi letadlem a pozemní stanicí
- Euklidovská vzdálenost
- Zachycovací metoda - grafická technika používaná v nebeské navigaci
- Laserový dálkoměr
- Multilateration - Adresuje multilateraci pseudo rozsahu
- Dálkoměr - systémy používané k měření vzdálenosti mezi dvěma body na zemi
- Resekce (orientace)
- SHORAN - Vyvinut jako vojenský letový navigační systém, později použitý pro civilní účely
- Zeměměřičství
- Tellurometr - první mikrovlnný elektronický dálkoměr
- Triangulace - metoda průzkumu založená na měření úhlů
Reference
externí odkazy
- stackexchange.com , implementace PHP / Python






![{\ Displaystyle {\ begin {aligned} r_ {1}^{2} & = x^{2}+y^{2} \\ [4pt] r_ {2}^{2} & = (Ux)^{ 2}+y^{2} \ end {zarovnaný}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75417a7cc7c30bde5d833ed87fd7bac94bdf7ce0)
![{\ displaystyle {\ begin {aligned} x & = {\ frac {r_ {1}^{2} -r_ {2}^{2}+U^{2}} {2U}} \\ [4pt] y & = \ pm {\ sqrt {r_ {1}^{2} -x^{2}}} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebcc6eb379df69ed08e8e83b5c4488c83481b3e3)

![{\ Displaystyle {\ begin {aligned} r_ {1}^{2} & = x^{2}+y^{2}+z^{2} \\ [4pt] r_ {2}^{2} & = (xU)^{2}+y^{2}+z^{2} \\ [4pt] r_ {3}^{2} & = (x-V_ {x})^{2}+(y -V_ {y})^{2}+z^{2} \ end {zarovnáno}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c79d1b3b07b4a53e3567564dd212e76f1146473e)

![{\ displaystyle {\ begin {aligned} x & = {\ frac {r_ {1}^{2} -r_ {2}^{2}+U^{2}} {2U}} \\ [4pt] y & = {\ frac {r_ {1}^{2} -r_ {3}^{2}+V^{2} -2V_ {x} x} {2V_ {y}}} \\ [4pt] z & = \ pm {\ sqrt {r_ {1}^{2} -x^{2} -y^{2}}} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfc991360d8b05be2e1aa68150d8c32a5543a6e8)



![{\ displaystyle {\ begin {aligned} x^{\ prime} & = {\ frac {(r_ {1}^{\ prime}+r_ {2}^{\ prime}) (r_ {1}^{\ prime} -r_ {2}^{\ prime})} {2U}} \\ [4pt] y^{\ prime} & = \ pm {\ frac {{\ sqrt {(r_ {1}^{\ prime }+r_ {2}^{\ prime})^{2} -U^{2}}} {\ sqrt {U^{2}-(r_ {1}^{\ prime} -r_ {2}^ {\ prime})^{2}}}} {2U}} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/656d76a6985f39c396e1a9bda6019b29877112fb)