Ukkonenův algoritmus - Ukkonen's algorithm

V počítačové vědě je Ukkonenův algoritmus online lineární algoritmus pro konstrukci stromů přípon , který navrhl Esko Ukkonen v roce 1995. Algoritmus začíná stromem implicitních přípon obsahujícím první znak řetězce. Poté projde řetězcem a přidává postupné znaky, dokud není strom úplný. Toto pořadí přidání znaků dává Ukkonenovu algoritmu jeho vlastnost „on-line“. Původní algoritmus představený Peterem Weinerem postupoval zpět od posledního znaku k prvnímu od nejkratší po nejdelší příponu. Jednodušší algoritmus našel Edward M. McCreight od nejdelší po nejkratší příponu.

Strom implicitní přípony

Při generování stromu přípon pomocí Ukkonenova algoritmu uvidíme strom implicitní přípony v mezikrokech v závislosti na znakech v řetězci S. V implicitních stromech přípon nebude existovat hrana se štítkem $ (nebo jakýmkoli jiným ukončovacím znakem) a žádný vnitřní uzel pouze s jedna hrana jde ven.

Vysoká úroveň popisu Ukkonenova algoritmu

Ukkonenův algoritmus konstruuje strom implicitní přípony T i pro každou předponu S [l ... i] S (S je řetězec délky n). Nejprve se vytvoří T 1 za použití 1 st znak a T 2 pomocí 2 nd znak, pak T 3 se za použití 3 rd charakter, ..., T n za použití n -té charakter. Ve stromu přípon, který používá Ukkonenův algoritmus, najdete následující charakteristiky:

  • Strom implicitní přípony T i +1 je postaven na vrcholu stromu implicitní přípony T i .
  • V každém daném okamžiku Ukkonenův algoritmus sestaví strom přípon pro dosud viděné znaky, a proto má vlastnost on-line , což umožňuje algoritmu mít čas provedení O (n).
  • Ukkonenův algoritmus je rozdělen do n fází (jedna fáze pro každý znak v řetězci o délce n).
  • Každá fáze i+1 je dále rozdělena na i+1 rozšíření, jedno pro každou z přípon i+1 S [1 ... i+1].

Rozšíření přípony je o přidání dalšího znaku do dosud vytvořeného stromu přípon. V prodloužení j fáze i+1 algoritmus najde konec S [j ... i] (který je již ve stromu kvůli předchozí fázi i) a poté pro jistotu rozšíří S [j ... i] přípona S [j ... i+1] je ve stromu. Existují tři pravidla rozšíření:

  1. Pokud cesta od kořene označeného S [j ... i] končí na okraji listu (tj. S [i] je poslední znak na okraji listu), pak je znak S [i+1] přidán pouze na konec štítku na tom okraji listu.
  2. pokud cesta od kořene označeného S [j ... i] končí na nelistové hraně (tj. za S [i] na cestě je více znaků) a další znak není S [i+1], pak nový hrana listu se štítkem S [i+1] a číslem j se vytvoří počínaje znakem S [i+1]. Nový vnitřní uzel bude také vytvořen, pokud S [1 ... i] skončí uvnitř (mezi nimi) nelistové hrany.
  3. Pokud cesta z kořene označeného S [j..i] končí na nelistové hraně (tj. Na cestě je více znaků za S [i]) a další znak je s [i+1] (již ve stromu), nedělat nic.

Jedním důležitým bodem, který je třeba poznamenat, je, že z daného uzlu (kořenového nebo interního) bude jeden a pouze jeden okraj začínající od jednoho znaku. Z žádného uzlu nebude vycházet více než jedna hrana, počínaje stejným znakem.

Doba běhu

Naivní implementace pro generování stromu přípon do budoucna vyžaduje časovou složitost O ( n 2 ) nebo dokonce O ( n 3 ) ve velké notaci O , kde n je délka řetězce. Využitím řady algoritmických technik Ukkonen toto zkrátil na O ( n ) (lineární) čas pro abecedy konstantní velikosti a O ( n log n ) obecně, což odpovídá běhovému výkonu předchozích dvou algoritmů.

Příklad Ukkonenova algoritmu

Konečná obrazovka přípony pomocí Ukkonenova algoritmu (příklad).

Abychom lépe ilustrovali, jak je konstruován strom přípon pomocí Ukkonenova algoritmu, můžeme použít následující příklad:

S = xabxac

  1. Začněte s prázdným kořenovým uzlem.
  2. Sestrojte T 1 pro S [1] přidáním prvního znaku řetězce. Platí pravidlo 2, které vytvoří nový listový uzel.
  3. Sestrojte T 2 pro S [1 ... 2] přidáním přípon xa (xa a a). Platí pravidlo 1, které rozšiřuje popis cesty ve stávajícím okraji listu. Platí pravidlo 2, které vytvoří nový listový uzel.
  4. Sestrojte T 3 pro S [1 ... 3] přidáním přípon xab (xab, ab a b). Platí pravidlo 1, které rozšiřuje popis cesty ve stávajícím okraji listu. Platí pravidlo 2, které vytvoří nový listový uzel.
  5. Sestrojte T 4 pro S [1 ... 4] přidáním přípon xabx (xabx, abx, bx a x). Platí pravidlo 1, které rozšiřuje popis cesty ve stávajícím okraji listu. Platí pravidlo 3, nedělejte nic.
  6. Sestaví T 5 pro S [1 ... 5] přidáním přípon xabxa (xabxa, abxa, bxa, xa a x). Platí pravidlo 1, které rozšiřuje popis cesty ve stávajícím okraji listu. Platí pravidlo 3, nedělejte nic.
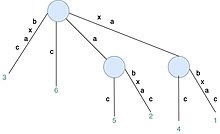
  7. Sestaví T 6 pro S [1 ... 6] přidáním přípon xabxac (xabxac, abxac, bxac, xac, ac a c). Platí pravidlo 1, které rozšiřuje popis cesty ve stávajícím okraji listu. Platí pravidlo 2, které vytvoří nový listový uzel (v tomto případě se vytvoří tři nové náběžné hrany a dva nové vnitřní uzly).

Reference

  1. ^ Ukkonen, E. (1995). „On-line konstrukce stromů přípon“ (PDF) . Algorithmica . 14 (3): 249–260. CiteSeerX  10.1.1.10.751 . doi : 10,1007/BF01206331 . S2CID  6027556 .
  2. ^ Weiner, Peter (1973). „Algoritmy pro porovnávání lineárních vzorů“ (PDF) . 14. výroční sympozium o teorii přepínání a automatů (SWAT 1973) . s. 1–11. CiteSeerX  10.1.1.474.9582 . doi : 10.1109/SWAT.1973.13 .
  3. ^ McCreight, Edward Meyers (1976). „Prostorově ekonomický příponový stromový konstrukční algoritmus“. Deník ACM . 23 (2): 262–272. CiteSeerX  10.1.1.130.8022 . doi : 10,1145/321941,321946 . S2CID  9250303 .

externí odkazy


Stub ikona

Tento článek související s algoritmy nebo datovými strukturami je útržek . Wikipedii můžete pomoci jejím rozšířením .