Vektorový prostor - Vector space
V matematice , fyzice a strojírenství je vektorový prostor (nazývaný také lineární prostor ) sada objektů nazývaných vektory , které lze sčítat a násobit („škálovat“) čísly zvanými skaláry . Skaláry jsou často reálná čísla , ale některé vektorové prostory mají skalární násobení komplexními čísly nebo obecně skalárem z jakéhokoli matematického pole . Operace sčítání vektorů a skalárního násobení musí splňovat určité požadavky, nazývané vektorové axiomy (uvedené níže v § Definice ). Chcete -li určit, zda jsou skaláry v konkrétním vektorovém prostoru skutečná čísla nebo komplexní čísla, často se používají termíny skutečný vektorový prostor a komplexní vektorový prostor .
Některé sady euklidovských vektorů jsou běžnými příklady vektorového prostoru. Představují fyzikální veličiny, jako jsou síly , kde lze přidat jakékoli dvě síly stejného typu, aby se získala třetina, a dalším vektorem sil je násobení silového vektoru skutečným multiplikátorem. Stejným způsobem (ale ve více geometrickém smyslu) vektory představující posuny v rovině nebo trojrozměrném prostoru také vytvářejí vektorové prostory. Vektory ve vektorových prostorech nemusí být nutně objekty podobné šipkám, jak se objevují ve zmíněných příkladech: vektory jsou považovány za abstraktní matematické objekty se zvláštními vlastnostmi, které lze v některých případech zobrazit jako šipky.
Vektorové prostory jsou předmětem lineární algebry a jsou dobře charakterizovány svou dimenzí , která, zhruba řečeno, určuje počet nezávislých směrů v prostoru. Nekonečně dimenzionální vektorové prostory přirozeně vznikají v matematické analýze jako funkční prostory , jejichž vektory jsou funkce . Tyto vektorové prostory jsou obecně vybaveny nějakou další strukturou, jako je topologie , která umožňuje zohlednění problémů blízkosti a spojitosti . Mezi těmito topologiemi se běžně používají ty, které jsou definovány normou nebo vnitřním produktem (jsou vybaveny pojmem vzdálenosti mezi dvěma vektory). To platí zejména pro Banachovy a Hilbertovy prostory , které jsou zásadní v matematické analýze.
Historicky lze první myšlenky vedoucí k vektorovým prostorům vysledovat až od analytické geometrie 17. století , matic , soustav lineárních rovnic a euklidovských vektorů. Moderní, abstraktnější zpracování, poprvé formulované Giuseppem Peanem v roce 1888, zahrnuje více obecných objektů než euklidovský prostor , ale velkou část teorie lze považovat za rozšíření klasických geometrických představ, jako jsou čáry , roviny a jejich vyšší dimenzionální analogie.
Dnes se vektorové prostory uplatňují v matematice , vědě a strojírenství . Jsou vhodným lineárně-algebraickým pojmem pro řešení soustav lineárních rovnic . Nabízejí rámec pro Fourierovu expanzi , která se používá v rutinách komprese obrazu , a poskytují prostředí, které lze použít pro techniky řešení parciálních diferenciálních rovnic . Kromě toho vektorové prostory poskytují abstraktní, bez souřadnic způsob řešení geometrických a fyzických objektů, jako jsou tenzory . To zase umožňuje zkoumání lokálních vlastností potrubí linearizačními technikami. Vektorový prostor lze generalizovat několika způsoby, což vede k pokročilejším pojmům v geometrii a abstraktní algebře .
Tento článek se zabývá hlavně vektorovými prostory s konečnou dimenzí. Mnoho principů však platí také pro nekonečně dimenzionální vektorové prostory.
| Algebraické struktury |
|---|
Úvod a definice
Nejprve jsou popsány dva typické příklady vektorového prostoru a poté je zavedena definice vektorových prostorů.
První příklad: šipky v rovině
První příklad vektorového prostoru se skládá ze šipek v pevné rovině , začínajících v jednom pevném bodě. To se ve fyzice používá k popisu sil nebo rychlostí . Vzhledem k jakýmkoli dvěma takovým šipkám, v a w , rovnoběžník překlenutý těmito dvěma šipkami obsahuje jednu diagonální šipku, která začíná také na počátku. Tato nová šipka se nazývá součet dvou šipek a označuje se v + w . Ve zvláštním případě dvou šipek na stejné přímce je jejich součet šipka na této přímce, jejíž délka je součtem nebo rozdílem délek, podle toho, zda mají šipky stejný směr. Další operace, která může být provedena s šipkami je měřítko: vzhledem k tomu, jakékoli kladné reálné číslo , šipka, že má stejný směr jako V , ale je rozšířené nebo sražená vynásobením jeho délky , se nazývá násobení z V podle . To je označováno na V . Když a je záporné, a v je definována jako šipka ukazující v opačném směru.
Následující příklad ukazuje několik příkladů: pokud a = 2 , výsledný vektor a w má stejný směr jako w , ale je natažen na dvojnásobnou délku w (pravý obrázek níže). Ekvivalentně 2 w je součet w + w . Navíc (−1) v = - v má opačný směr a stejnou délku jako v (modrý vektor směřující dolů na pravý obrázek).

|
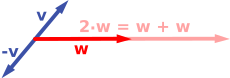
|
Druhý příklad: seřazené dvojice čísel
Druhý klíčový příklad vektorového prostoru poskytují dvojice reálných čísel x a y . (Pořadí složek x a y je významné, proto se takové dvojici také říká uspořádaná dvojice .) Taková dvojice se zapisuje jako ( x , y ) . Součet dvou takových párů a násobení páru číslem je definován následovně:
a
První příklad výše se redukuje na tento příklad, pokud je šipka reprezentována dvojicí kartézských souřadnic jejího koncového bodu.
Definice
V tomto článku jsou vektory znázorněny tučně, aby se odlišily od skalárů.
Vektorový prostor nad polem F je množina V spolu se dvěma operacemi, které splňují osm níže uvedených axiomů. V následujícím textu, V x V označuje kartézský součin z V se sebou samým, a → označuje mapování z jednoho souboru do druhého.
- První operace, nazývaná sčítání vektorů nebo jednoduše sčítání +: V × V → V , vezme libovolné dva vektory v a w a přiřadí jim třetí vektor, který se běžně zapisuje jako v + w , a nazývá se součtem těchto dvou vektorů. (Výsledný vektor je také prvkem množiny V. )
- Druhá operace, nazývaná skalární násobení ·: F × V → V, vezme jakýkoli skalární a a jakýkoli vektor v a dá další vektor a v . (Podobně je vektor a v prvkem množiny V. Skalární násobení nelze zaměňovat se skalárním součinem , nazývaným také vnitřní součin nebo bodový součin , což je další struktura přítomná v některých konkrétních, ale ne ve všech vektorových prostorech . Skalární násobení je násobení vektoru podle skalár, druhý je násobení dvou vektorů produkujících skalární).
Prvkům V se běžně říká vektory . Prvkům F se běžně říká skaláry . Společné symboly pro označení vektorových prostorů zahrnují U , V a W .
Ve dvou výše uvedených příkladech je pole pole skutečných čísel a množina vektorů se skládá z rovinných šipek s pevným počátečním bodem a dvojic reálných čísel.
Aby byla sada V a operace sčítání vektorů a skalárního násobení kvalifikovány jako vektorový prostor, musí splňovat řadu požadavků nazývaných axiomy . Tyto jsou uvedeny v následující tabulce, kde u , V a W pozadím označují libovolných vektorů V a A a b označují skaláry v F .
| Axiom | Význam |
|---|---|
| Asociativita sčítání vektorů | u + ( v + w ) = ( u + v ) + w |
| Komutativita sčítání vektorů | u + v = v + u |
| Prvek identity přidávání vektorů | Existuje prvek 0 ∈ V , nazvaný nulový vektor , tak, že v + 0 = v pro všechny v ∈ V . |
| Inverzní prvky vektorového sčítání | Pro každý v ∈ V existuje prvek - v ∈ V , nazvaný přísada inverzní z V , takže v + (- v ) = 0 . |
| Kompatibilita skalárního násobení s násobením pole | a ( b v ) = ( ab ) v |
| Prvek identity skalárního násobení | 1 v = objem , kde 1 označuje multiplikativní identita v F . |
| Distribučnost skalárního násobení s ohledem na přidání vektoru | a ( u + v ) = a u + a v |
| Distribučnost skalárního násobení s ohledem na sčítání polí | ( a + b ) v = a v + b v |
Tyto axiomy zobecňují vlastnosti vektorů zavedených ve výše uvedených příkladech. Výsledek sčítání dvou uspořádaných dvojic (jako ve druhém příkladu výše) skutečně nezávisí na pořadí součtů:
- ( x v , y v ) + ( x w , y w ) = ( x w , y w ) + ( x v , y v ) .
Podobně v geometrickém příkladu vektorů jako šipek v + w = w + v, protože rovnoběžník definující součet vektorů je nezávislý na pořadí vektorů. Všechny ostatní axiomy lze ověřit podobným způsobem v obou příkladech. Bez ohledu na konkrétní povahu konkrétního typu vektorů zahrnuje definice tyto dva a mnoho dalších příkladů do jednoho pojmu vektorového prostoru.
Odčítání dvou vektorů a dělení (nenulovým) skalárem lze definovat jako
Když skalární pole F jsou skutečná čísla R , vektorový prostor se nazývá skutečný vektorový prostor . Když je skalárním polem komplexní čísla C , vektorový prostor se nazývá komplexní vektorový prostor . Tyto dva případy se nejčastěji používají ve strojírenství. Obecná definice vektorového prostoru umožňuje skalární být prvky jakékoliv pevné pole F . Pojem je pak známý jako F - vektorového prostoru nebo vektorový prostor nad F . Pole je v podstatě množina čísel, která mají operace sčítání , odčítání , násobení a dělení . Racionální čísla například tvoří pole.
Na rozdíl od intuice pramenící z vektorů v rovině a ve vyšších dimenzích v obecných vektorových prostorech neexistuje pojem blízkost , úhly ani vzdálenosti . Abychom se s takovými záležitostmi vypořádali, jsou zavedeny konkrétní typy vektorových prostorů; více viz § Vektorové mezery s další strukturou níže.
Alternativní formulace a elementární důsledky
Vektorové sčítání a skalární násobení jsou operace, které splňují uzavírací vlastnosti: u + v a v jsou v V pro všechny A v F , a u , v v V . Některé starší zdroje uvádějí tyto vlastnosti jako samostatné axiomy.
V řeči abstraktní algebry jsou první čtyři axiomy ekvivalentní požadavku, aby množina vektorů byla abelianskou skupinou pod přídavkem. Zbývající Axiómy by této skupině je F - modul strukturu. Jinými slovy, existuje kruhový homomorfismus f z pole F do endomorfistického kruhu skupiny vektorů. Potom je skalární násobení a v definováno jako ( f ( a )) ( v ) .
Axiomy vektorového prostoru mají řadu přímých důsledků. Některé z nich jsou odvozeny z elementární teorii skupiny , aplikovaného na aditivní skupiny vektorů: například nulový vektor 0 z V a přísada inverzní - v jakékoliv vektoru V jsou jedinečné. Další vlastnosti následují s využitím distribučního zákona pro skalární násobení, například a v se rovná 0 právě tehdy, když se a rovná 0 nebo v se rovná 0 .
Dějiny
Vektorové prostory pocházejí z afinní geometrie zavedením souřadnic v rovině nebo trojrozměrném prostoru. Kolem roku 1636 založili francouzští matematici René Descartes a Pierre de Fermat analytickou geometrii identifikací řešení rovnice dvou proměnných s body na rovinné křivce . Aby bylo možné dosáhnout geometrických řešení bez použití souřadnic, zavedl Bolzano v roce 1804 určité operace s body, přímkami a rovinami, které jsou předchůdci vektorů. Möbius (1827) představil pojem barycentrických souřadnic . Bellavitis (1833) zavedl pojem bipoint, tj. Orientovaný segment, jehož jeden konec je původem a druhý cílem. Vektory byly přezkoumány za prezentaci komplexních čísel ze strany Argand a Hamilton a vznikem čtveřic ze strany druhé. Jsou to prvky v R 2 a R 4 ; jejich zpracování pomocí lineárních kombinací sahá až k Laguerrovi v roce 1867, který také definoval systémy lineárních rovnic .
V roce 1857 Cayley představil maticový zápis, který umožňuje harmonizaci a zjednodušení lineárních map . Přibližně ve stejnou dobu Grassmann studoval barycentrický počet iniciovaný Möbiusem. Předpokládal sady abstraktních objektů, které byly vybaveny operacemi. V jeho práci jsou přítomny koncepty lineární nezávislosti a dimenze , stejně jako skalární produkty . Ve skutečnosti Grassmannova práce z roku 1844 přesahuje rámec vektorových prostorů, protože i jeho uvažování o násobení ho přivedlo k tomu, čemu se dnes říká algebry . Italský matematik Peano byl první, kdo v roce 1888 poskytl moderní definici vektorových prostorů a lineárních map.
Důležitý vývoj vektorových prostorů je kvůli stavbě prostorů funkcí u Henri Lebesgueův . To bylo později formalizováno Banachem a Hilbertem , kolem roku 1920. V té době začala interagovat algebra a nové pole funkční analýzy , zejména s klíčovými pojmy, jako jsou prostory p -integrovatelných funkcí a Hilbertovy prostory . Také v této době byly provedeny první studie týkající se nekonečně dimenzionálních vektorových prostorů.
Příklady
Souřadnicový prostor
Nejjednodušším příkladem vektorového prostoru nad polem F je samotné pole F (protože jde o abelianskou skupinu pro sčítání, součást požadavků na pole .), Vybavené jeho sčítáním (stává se vektorovým sčítáním) a násobením (Stává se skalárním násobením.) Obecněji řečeno, všechny n -tuple (sekvence délky n )
- ( a 1 , a 2 , ..., a n )
prvků a i z F tvoří vektorový prostor, který je obvykle označován F n a nazývá se souřadnicovým prostorem . Případ n = 1 je výše uvedený nejjednodušší příklad, ve kterém je pole F také považováno za vektorový prostor nad sebou. Případ F = R a n = 2 (tak, R 2 ), byla diskutována v úvodu výše.
Komplexní čísla a další rozšíření polí
Množina komplexních čísel C , tj. Čísel, která lze zapsat ve tvaru x + iy pro reálná čísla x a y, kde i je imaginární jednotka , tvoří vektorový prostor nad realitami s obvyklým sčítáním a násobením: ( x + iy ) + ( a + ib ) = ( x + a ) + i ( y + b ) a c ⋅ ( x + iy ) = ( c ⋅ x ) + i ( c ⋅ y ) pro reálná čísla x , y , a , b a c . Různé axiomy vektorového prostoru vyplývají ze skutečnosti, že stejná pravidla platí pro aritmetiku komplexních čísel.
Ve skutečnosti je příklad komplexních čísel v podstatě stejný jako (to znamená, že je izomorfní ) pro vektorový prostor uspořádaných dvojic reálných čísel uvedených výše: uvažujeme -li o komplexním čísle x + i y , které představuje uspořádaný pár ( x , y ) v komplexní rovině pak vidíme, že pravidla pro sčítání a skalární násobení odpovídají přesně těm v předchozím příkladu.
Obecněji řečeno, rozšíření pole představují další třídu příklady vektorových prostorů, a to zejména v algebře a algebraické teorie čísel : pole F obsahuje menší pole E je E -vector prostor, podle daných násobení a adičních operace F . Například, komplexní čísla jsou vektorový prostor přes R , a rozšíření pole je vektorový prostor nad Q .
Funkční mezery
Funkce z jakékoli pevné množiny Ω do pole F také vytvářejí vektorové mezery prováděním bodového sčítání a skalárního násobení. To znamená, že součet dvou funkcí f a g je funkce ( f + g ) daná vztahem
- ( f + g ) ( w ) = f ( w ) + g ( w ) ,
a podobně pro násobení. Takové funkční prostory se vyskytují v mnoha geometrických situacích, kdy Ω je reálná osa nebo intervalu , nebo jiné podskupiny z R . Mnoho pojmy v topologii a analýzu, jako je kontinuita , integrability nebo diferencovatelnosti jsou dobře choval ve vztahu k linearity: součty a skalární násobky funkcí které mají takové vlastnosti ještě tu vlastnost. Proto jsou množinou takových funkcí vektorové mezery. Jsou podrobněji studovány pomocí metod funkční analýzy , viz níže . Algebraická omezení také dávají vektorové prostory: vektorový prostor F [x] je dán polynomiálními funkcemi :
- f ( x ) = r 0 + r 1 x + ... + r n -1 x n -1 + r n x n , kde koeficienty r 0 , ..., r n , jsou v F .
Lineární rovnice
Systémy homogenních lineárních rovnic jsou úzce svázány s vektorovými prostory. Například řešení
A + 3 b + C = 0 4 a + 2 b + 2 c = 0
jsou dány trojkami s libovolnými a , b = a /2 a c = −5 a /2 . Tvoří vektorový prostor: součty a skalární násobky takových trojic stále uspokojují stejné poměry tří proměnných; jsou tedy také řešením. Matice mohou být použity ke kondenzaci více lineárních rovnic, jak je uvedeno výše, do jedné vektorové rovnice, jmenovitě
- A x = 0 ,
kde je matice obsahující koeficienty daných rovnic, x je vektor ( a , b , c ) , A x označuje součin matice a 0 = (0, 0) je nulový vektor. V podobném duchu tvoří řešení homogenních lineárních diferenciálních rovnic vektorové prostory. Například,
- f ′ ′ ( x ) + 2 f ′ ( x ) + f ( x ) = 0
dává f ( x ) = a e - x + bx e - x , kde a a b jsou libovolné konstanty, a e x je přirozená exponenciální funkce .
Základ a rozměr

Báze umožňují reprezentovat vektory sekvencí skalárů nazývaných souřadnice nebo komponenty . Základem je množina B = { b i } i ∈ I vektorů b i , pro pohodlí často indexovaná nějakou indexovou sadou I , která zabírá celý prostor a je lineárně nezávislá . „Rozložení celého prostoru“ znamená, že jakýkoli vektor v lze vyjádřit jako konečný součet (nazývaný lineární kombinace ) základních prvků:
-
( 1 )
kde k jsou skalární, tzv souřadnicemi (nebo jejich složky) vektoru V s ohledem na základ B , a b i k ( k = 1, ..., n ), prvky B . Lineární nezávislost znamená, že souřadnice a k jsou jednoznačně určeny pro jakýkoli vektor ve vektorovém prostoru.
Například souřadnicové vektory e 1 = (1, 0,…, 0) , e 2 = (0, 1, 0,…, 0) , až e n = (0, 0,…, 0, 1) , tvoří základ F n , nazývaný standardní základ , protože jakýkoli vektor ( x 1 , x 2 , ..., x n ) lze jednoznačně vyjádřit jako lineární kombinaci těchto vektorů:
- ( x 1 , x 2 ,…, x n ) = x 1 (1, 0,…, 0) + x 2 (0, 1, 0,…, 0) + ⋯ + x n (0,…, 0, 1) = x 1 e 1 + x 2 e 2 + ⋯ + x n e n .
Odpovídající souřadnice x 1 , x 2 , … , x n jsou jen karteziánské souřadnice vektoru.
Každý vektorový prostor má svůj základ. Vyplývá to ze Zornova lemmatu , ekvivalentní formulace Axiom of Choice . S ohledem na další axiomy teorie množin Zermelo – Fraenkel je existence základů ekvivalentní axiomu volby. Ultrafilter lemma , který je slabší než axiomu výběru, znamená, že všechny základny daného vektorového prostoru mají stejný počet prvků, nebo mohutnost (viz rozměr věta pro vektorových prostorech ). To se nazývá dimenze vektorového prostoru, označil dim V . Pokud prostor zabírá konečný počet vektorů, lze výše uvedená tvrzení dokázat bez tak zásadního vstupu z teorie množin.
Dimenze souřadnicového prostoru F n je n , podle báze ukázané výše. Rozměr polynomu kroužku F [ x ] zavedla výše se countably nekonečný , základna je dána 1 , x , x 2 , ... Tím spíše je rozměr obecnějších prostorů funkcí, jako je například prostoru funkcí na některých (ohraničená nebo neomezený) interval, je nekonečný. Za vhodných předpokladů pravidelnosti příslušných koeficientů se rozměr prostoru řešení homogenní obyčejné diferenciální rovnice rovná stupni rovnice. Prostor řešení pro výše uvedenou rovnici je například generován e - x a xe - x . Tyto dvě funkce jsou lineárně nezávislé na R , takže rozměr tohoto prostoru je dva, stejně jako stupeň rovnice.
Rozšíření pole nad racionály Q lze považovat za vektorový prostor nad Q (definováním přidání vektoru jako přidání pole, definováním skalárního násobení jako násobení pole prvky Q a jinak ignorováním násobení pole). Dimenze (nebo stupeň ) rozšíření pole Q ( α ) přes Q závisí na α . Pokud α splňuje nějakou polynomickou rovnici
Lineární mapy a matice
Vztah dvou vektorových prostorů lze vyjádřit lineární mapou nebo lineární transformací . Jsou to funkce, které odrážejí strukturu vektorového prostoru, to znamená, že zachovávají součty a skalární násobení:
- a f ( · v ) = · f ( v ) pro všechny V a W v V , všechny v F .
Izomorfismus je lineární mapa f : V → W tak, že existuje inverzní mapa g : W → V , který je mapa tak, že dvě možné prostředky f ∘ g : W → W a g ∘ f : V → V jsou mapy identity . Ekvivalentně je f jak one-to-one ( injektivní ), tak na ( surjektivní ). Existuje -li mezi V a W izomorfismus , pak se říká, že tyto dva prostory jsou izomorfní ; pak jsou v podstatě totožné jako vektorové prostory, protože všechny identity držící ve V jsou přes f transportovány do podobných ve W a naopak přes g .
Například vektorové prostory „šipky v rovině“ a „uspořádané dvojice čísel“ v úvodu jsou izomorfní: planární šipka v odcházející na počátku nějakého (pevného) souřadného systému může být vyjádřena jako uspořádaná dvojice uvažováním x - a y - součást šipky, jak je znázorněno na obrázku vpravo. Naopak vzhledem k dvojici ( x , y ) se šipkou od x na pravé straně (nebo na levé straně, pokud x je negativní), a y nahoru (dolů, pokud y je negativní) otočí se šipkou V .
Lineární mapy V → W mezi dvěma vektorovými prostory tvoří vektorový prostor Hom F ( V , W ) , označovaný také L ( V , W ) nebo 𝓛 ( V , W ) . Prostor lineárních map od V do F se nazývá duální vektorový prostor , označovaný V ∗ . Prostřednictvím injektivní přirozené mapy V → V ∗∗ lze do jejího bidualu vložit jakýkoli vektorový prostor ; mapa je izomorfismus jen tehdy, je-li prostor konečno-dimenzionální.
Jakmile je zvolen základ V , lineární mapy f : V → W jsou zcela určeny specifikací obrazů základních vektorů, protože jakýkoli prvek V je vyjádřen jednoznačně jako jejich lineární kombinace. Pokud dim V = dim W , je 1-k-1 korespondence mezi pevnými základy V a W vede k lineární mapu, která mapuje žádný základ prvek V na odpovídající základní prvek W . Podle své definice je to izomorfismus. Dva vektorové prostory jsou tedy izomorfní, pokud se jejich rozměry shodují a naopak. Další způsob, jak to vyjádřit, je, že jakýkoli vektorový prostor je zcela klasifikován ( až do izomorfismu) podle své dimenze, jediného čísla. Zejména jakýkoli n -rozměrný F -vektorový prostor V je izomorfní s F n . Neexistuje však žádný „kanonický“ nebo preferovaný izomorfismus; vlastně izomorfismus φ : F n → V je ekvivalentní volbě báze V , mapováním standardního základu F n na V , přes φ . Svoboda volby vhodného základu je obzvláště užitečná v nekonečně dimenzionálním kontextu; viz níže .
Matice
Matice jsou užitečným pojmem pro kódování lineárních map. Jsou zapsány jako obdélníkové pole skalárů jako na obrázku vpravo. Libovolná m -by- n matice A vede k lineární mapě od F n do F m následujícím způsobem
- , kde označuje součet ,
nebo pomocí násobení matice matice A souřadnicovým vektorem x :
- x ↦ A x .
Navíc po výběru základen V a W je jakákoli lineární mapa f : V → W jednoznačně reprezentována maticí prostřednictvím tohoto přiřazení.
Determinant det ( ) z čtvercové matice A je skalární, který říká, zda je související mapě je izomorfismus, nebo ne: být tak, že je nezbytné a dostačující, že determinant je nenulový. Lineární transformace R n odpovídající reálné matici n -by -n zachovává orientaci tehdy a jen tehdy, je -li její determinant kladný.
Vlastní čísla a vlastní vektory
Endomorfismy , lineární mapy f : V → V , jsou zvláště důležité, protože v tomto případě lze vektory v porovnat s jejich obrazem pod f , f ( v ) . Každý nenulový vektor v uspokojující lambda V = f ( V ) , kde λ je skalární, se nazývá vlastní vektor o f s vlastní číslo λ . Ekvivalentně v je prvek jádra rozdílu f - λ · Id (kde Id je mapa identity V → V ) . Pokud je V konečná dimenze, lze to přepsat pomocí determinantů: f s vlastní hodnotou λ je ekvivalentní
- det ( f - λ · Id) = 0 .
Pomocí hláskování definici determinantu, výraz na levé straně je patrné, že je polynomiální funkce v lambda , nazvaný charakteristický polynom z f . Pokud je pole F dostatečně velké, aby obsahovalo nulu tohoto polynomu (což se automaticky stane pro F algebraicky uzavřené , například F = C ), má každá lineární mapa alespoň jeden vlastní vektor. Vektorový prostor V může, ale nemusí mít vlastní základnu , základ sestávající z vlastních vektorů. Tento jev se řídí kanonickou formou mapy Jordánu . Množina všech vlastních vektorů odpovídajících konkrétnímu vlastnímu číslu f tvoří vektorový prostor známý jako vlastní prostor odpovídající příslušnému vlastnímu číslu (a f ). K dosažení spektrální věty , odpovídající tvrzení v nekonečně dimenzionálním případě, je zapotřebí aparát funkční analýzy, viz níže .
Základní konstrukce
Kromě výše uvedených konkrétních příkladů existuje řada standardních lineárních algebraických konstrukcí, které poskytují vektorové prostory související s danými. Kromě níže uvedených definic se vyznačují také univerzálními vlastnostmi , které určují objekt X zadáním lineárních map z X do jakéhokoli jiného vektorového prostoru.
Podprostory a kvocientové mezery
Neprázdná podmnožina W vektorového prostoru V, který je uzavřen v sčítání a skalární násobení (a proto obsahuje 0 -vector na V ) se nazývá lineární podprostor z V , nebo jednoduše podprostor z V , když je okolní prostor je jednoznačně vektorový prostor. Subprostory V jsou vektorové mezery (nad stejným polem) samy o sobě. Průsečík všech podprostorů, které obsahují daný soubor S vektorů se nazývá jeho rozsah , a to je nejmenší podprostor V, která obsahuje soubor S . Vyjádřeno prvků, přičemž rozpětí je podprostor sestávající ze všech lineárních kombinací prvků ze S .
Lineární podprostor dimenze 1 je vektorová čára . Lineární podprostor dimenze 2 je vektorová rovina . Lineární podprostor, který obsahuje všechny prvky kromě jednoho ze základů okolního prostoru, je vektorová hyperplane . Ve vektorovém prostoru konečné dimenze n je vektorová hyperplana tedy podprostorem dimenze n - 1 .
Protějšek podprostorů jsou kvocienty vektorových prostorů . Vzhledem k jakémukoli podprostoru W ⊂ V je kvocient prostoru V / W („ V modulo W “) definován následovně: jako množina se skládá z v + W = { v + w : w ∈ W }, kde v je libovolný vektor v . Součet obou těchto prvků v 1 + W a V 2 + W je ( v 1 + V 2 ) + W , a skalární násobení je dána v · ( V + W ) = ( s · V ) + W . Klíčovým bodem je v této definice je to, že v 1 + W = V 2 + W tehdy a jen tehdy, pokud je rozdíl v 1 a v 2 spočívá ve W . Tímto způsobem se informace o Prostor kvocientu „zapomene“, která je obsažena v subprostorového W .
Jádro ker ( f ) lineárního mapě f : V → W sestává z vektorů V, které jsou mapovány na 0 ° C v W . Jádro a obrázek im ( f ) = { f ( v ): v ∈ V } jsou podprostory V a W , v daném pořadí. Existence jader a obrázků je součástí tvrzení, že kategorie vektorových prostorů (nad pevným polem F ) je abelianská kategorie , tj. Korpus matematických objektů a mapy zachovávající strukturu mezi nimi ( kategorie ), která se chová podobně jako kategorie abelianských skupin . Z tohoto důvodu mnoho prohlášení, jako je první věta o izomorfismu (také nazývaná věta o hodnosti a nule v pojmech souvisejících s maticí)
- V / ker ( f ) ≡ im ( f ).
a druhou a třetí větu o izomorfismu lze formulovat a dokázat způsobem velmi podobným odpovídajícím tvrzením pro skupiny .
Důležitým příkladem je jádro lineární mapy x ↦ A x pro nějakou pevnou matici A , jak je uvedeno výše . Jádro této mapy je podprostor vektorů x tak, že x = 0 , což je přesně množina řešení systému homogenních lineárních rovnic, které patří do A . Tento koncept se vztahuje také na lineární diferenciální rovnice
- , kde koeficienty a i jsou také funkce v x .
Na odpovídající mapě
- ,
že deriváty z funkce f objeví lineárně (na rozdíl od f '' ( x ) 2 , například). Protože diferenciace je lineární procedura (tj. ( F + g ) ′ = f ′ + g ′ a ( c · f ) ′ = c · f ′ pro konstantu c ), je toto přiřazení lineární, nazývá se lineární diferenciální operátor . Zejména řešení diferenciální rovnice D ( f ) = 0 tvoří vektorový prostor (nad R nebo C ).
Přímý produkt a přímá částka
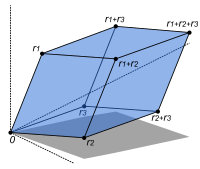
Přímý produkt vektorových prostorů a přímý součet vektorových prostorů jsou dva způsoby, kombinující indexovanou rodinu vektorových prostorů do nového vektorového prostoru.
Přímý produkt z rodiny vektorových prostorů v i se skládá z množiny všech n-tic ( v i ) i ∈ I , který udává pro každý index i v některých indexu nastavit I element V i o V i . Sčítání a skalární násobení se provádí po částech. Varianta této konstrukce je přímý součet (nazývaný také koprodukt a označován ), kde jsou povoleny pouze n -tice s konečným počtem nenulových vektorů. Pokud je množina indexů I konečná, obě konstrukce souhlasí, ale obecně se liší.
Tenzorový výrobek
Tensor produkt V ⊗ F W , nebo jednoduše V ⊗ W , o dva vektorové prostory V a W je jedním z ústředních pojmů multilineární algebry , která se zabývá probíhajících pojmů, jako je lineární mapy na několika proměnných. Mapa g : V × W → X se nazývá bilineární, pokud je g lineární v obou proměnných v a w . To znamená, že pro fixní w je mapa v ↦ g ( v , w ) lineární ve výše uvedeném smyslu a podobně pro fixní v .
Tensorový produkt je konkrétní vektorový prostor, který je univerzálním příjemcem bilineárních map g následujícím způsobem. Je definován jako vektorový prostor skládající se z konečných (formálních) součtů symbolů nazývaných tenzory
- v 1 ⊗ w 1 + v 2 ⊗ w 2 + ⋯ + v n ⊗ w n ,
podléhá pravidlům
- a · ( v ⊗ w ) = ( a · v ) ⊗ w = v ⊗ ( a · w ), kde a je skalární,
- ( v 1 + v 2 ) ⊗ w = v 1 ⊗ w + v 2 ⊗ w , a
- v ⊗ ( w 1 + w 2 ) = v ⊗ w 1 + v ⊗ w 2 .

Tato pravidla zajišťují, že mapa f od V × W do V ⊗ W, která mapuje n -tici ( v , w ) do v ⊗ w, je bilineární. Univerzálnost uvádí, že vzhledem k jakémukoli vektorovému prostoru X a každé bilineární mapě g : V × W → X existuje jedinečná mapa u , znázorněná na diagramu s tečkovanou šipkou, jejíž složení s f se rovná g : u ( v ⊗ w ) = g ( v , w ) . Tomu se říká univerzální vlastnost produktu tenzoru, instance metody - hodně používané v pokročilé abstraktní algebře - k nepřímému definování objektů zadáním map z nebo do tohoto objektu.
Vektorové prostory s další strukturou
Z hlediska lineární algebry jsou vektorové prostory zcela chápány, pokud je jakýkoli vektorový prostor charakterizován, až do izomorfismu, svou dimenzí. Avšak vektorové prostory samy o sobě nenabízejí rámec pro řešení otázky - zásadní pro analýzu - zda posloupnost funkcí konverguje k jiné funkci. Stejně tak lineární algebra není uzpůsobena pro práci s nekonečnými řadami , protože operace sčítání umožňuje přidat pouze konečný počet výrazů. Potřeby funkční analýzy proto vyžadují zvážení dalších struktur.
Vektorovému prostoru může být přiděleno dílčí pořadí ≤, za kterého lze některé vektory porovnávat. Například n -dimenzionální reálný prostor R n lze uspořádat porovnáním jeho vektorů po částech. Uspořádané vektorové prostory , například Rieszovy , jsou zásadní pro Lebesgueovu integraci , která se spoléhá na schopnost vyjádřit funkci jako rozdíl dvou kladných funkcí
- ,
kde označuje pozitivní část a negativní část.
Normované vektorové prostory a vnitřní produktové prostory
"Měření" vektorů se provádí zadáním normy , vztažného bodu, který měří délky vektorů, nebo vnitřním součinem , který měří úhly mezi vektory. Normy a vnitřní produkty jsou označeny a , v tomto pořadí. Počátek vnitřního produktu znamená, že lze definovat také délky vektorů definováním přidružené normy . Vektorové prostory vybavené takovými daty jsou známé jako normované vektorové prostory a vnitřní součinové prostory .
Souřadnicový prostor F n může být vybaven standardním bodovým produktem :
V R 2 to odráží společný pojem úhlu mezi dvěma vektory x a y podle kosinusového zákona :
Z tohoto důvodu se dva uspokojivé vektory nazývají ortogonální . V prostoru Minkowski se používá důležitá varianta standardního bodového produktu : R 4 s výrobkem Lorentz
Na rozdíl od standardního bodového produktu není pozitivní definitivní : bere také záporné hodnoty, například pro . Vyčlenění čtvrté souřadnice- odpovídající času , na rozdíl od tří prostorových dimenzí-je užitečné pro matematické zpracování speciální relativity .
Topologické vektorové prostory
Otázky konvergence jsou zpracovány uvažováním vektorových prostorů V nesoucích kompatibilní topologii , strukturu, která umožňuje hovořit o tom, že prvky jsou blízko sebe . Zde kompatibilní znamená, že sčítání a skalární násobení musí být spojité mapy . Zhruba, pokud se x a y ve V a a ve F liší o ohraničené množství, pak také x + y a a x . Aby měl smysl specifikovat skalární změny množství, musí pole F v tomto kontextu také nést topologii; běžnou volbou jsou reálná čísla nebo komplexní čísla.
V takových topologických vektorových prostorech lze uvažovat o řadě vektorů. Nekonečný součet
označuje hranici odpovídajících konečných částečných součtů sekvence ( f i ) i ∈ N prvků V . Například f i mohou být (skutečné nebo komplexní) funkce patřící do nějakého funkčního prostoru V , v takovém případě je řada funkční řadou . Způsob konvergence řady závisí na topologii uložené prostoru funkcí. V takových případech jsou bodové sbližování a jednotné sbližování dva prominentní příklady.

Způsob, jak zajistit existenci limitů určitých nekonečných řad, je omezit pozornost na prostory, kde má jakákoli Cauchyova posloupnost limit; takový vektorový prostor se nazývá úplný . Zhruba je vektorový prostor úplný za předpokladu, že obsahuje všechny potřebné limity. Například vektorový prostor polynomů na jednotkovém intervalu [0,1], vybavený topologií rovnoměrné konvergence, není úplný, protože jakoukoli spojitou funkci na [0,1] lze rovnoměrně aproximovat sekvencí polynomů, pomocí Weierstrassova aproximační věta . Naproti tomu prostor všech spojitých funkcí na [0,1] se stejnou topologií je úplný. Norma dává vzniknout topologii definováním, že posloupnost vektorů v n konverguje k v tehdy a jen tehdy
Banachův a Hilbertův prostor jsou úplné topologické vektorové prostory, jejichž topologie je dána normou a vnitřním součinem. Jejich studie-klíčový kus funkční analýzy-se zaměřuje na nekonečno-dimenzionální vektorové prostory, protože všechny normy na topologické vektorové prostory s konečnou dimenzí vedou ke stejnému pojmu konvergence. Obrázek vpravo ukazuje ekvivalenci 1-normy a ∞-normy na R 2 : jak se jednotka "koulí" vzájemně uzavírá, posloupnost konverguje k nule v jedné normě právě tehdy, pokud tomu tak je v druhé normě . V nekonečně dimenzionálním případě však obecně budou existovat nerovnoměrné topologie, což činí studium topologických vektorových prostorů bohatšími než ve vektorových prostorech bez dalších dat.
Z koncepčního hlediska by všechny pojmy související s topologickými vektorovými prostory měly odpovídat topologii. Například místo zvažování všech lineárních map (nazývaných také funkcionály ) V → W musí být mapy mezi topologickými vektorovými prostory spojité. Zejména (topologický) duální prostor V ∗ se skládá ze spojitých funkcionálů V → R (nebo do C ). Základní Hahnova – Banachova věta se zabývá oddělením podprostorů příslušných topologických vektorových prostorů spojitými funkcionály.
Banachovy prostory
Banachovy prostory , představené Stefanem Banachem , jsou úplné normované vektorové mezery.
Prvním příkladem je vektorový prostor skládající se z nekonečných vektorů se skutečnými položkami, jejichž -norm daný
- pro a .
Topologie v nekonečně dimenzionálním prostoru jsou pro různé nerovnoměrné . Sekvence vektorů , ve kterých jsou první komponenty a následující jsou , například konverguje k nulovému vektoru pro , ale ne pro :
- , ale
Obecněji než sekvence reálných čísel jsou funkce obdařeny normou, která nahrazuje výše uvedený součet Lebesgueovým integrálem
Prostor integrovatelných funkcí v daném oboru (například v intervalu), vyhovující , a vybavené této normy se nazývají Lebesgue prostor , označený .
Tyto prostory jsou kompletní. (Pokud místo toho použijeme Riemannův integrál , prostor není úplný, což lze považovat za ospravedlnění Lebesgueovy integrační teorie.) Konkrétně to znamená, že pro jakoukoli sekvenci Lebesgueových integrovatelných funkcí s splněním podmínky
existuje funkce patřící do vektorového prostoru tak, že
Uložení podmínek omezenosti nejen na funkci, ale také na její deriváty vede k Sobolevovým prostorům .
Hilbertovy prostory
Kompletní vnitřní produktové prostory jsou známé jako Hilbertovy prostory , na počest Davida Hilberta . Hilbertův prostor L 2 (Ω), s vnitřním součinem daným
kde označuje komplexní konjugát o g ( x ), je klíčovým případ.
Podle definice se v Hilbertově prostoru jakákoli Cauchyova posloupnost sbíhá do limitu. Na druhou stranu je stejně důležité najít posloupnost funkcí f n s požadovanými vlastnostmi, která se blíží dané mezní funkci. Včasná analýza pod záminkou Taylorovy aproximace stanovila aproximaci diferencovatelných funkcí f polynomy. Podle Stone -Weierstrassovy věty lze každou spojitou funkci na [ a , b ] aproximovat podle potřeby polynomem. Podobná aproximační technika pomocí goniometrických funkcí se běžně nazývá Fourierova expanze a je hodně používána ve strojírenství, viz níže . Obecněji a konceptuálněji poskytuje věta jednoduchý popis toho, jaké „základní funkce“, nebo v abstraktních Hilbertových prostorech, jaké základní vektory stačí k vytvoření Hilbertova prostoru H v tom smyslu, že uzavření jejich rozpětí (tj. (konečné lineární kombinace a jejich limity) je celý prostor. Taková sada funkcí se nazývá základ z H , jeho mohutnost je známý jako prostor rozměr Hilbertova . Věta nejenže ukazuje vhodné bazické funkce jako dostatečné pro účely aproximace, ale také společně s Gram -Schmidtovým procesem umožňuje konstruovat základ ortogonálních vektorů . Takové ortogonální báze jsou Hilbertovým zobecněním souřadnicových os v konečném dimenzionálním euklidovském prostoru .
Řešení různých diferenciálních rovnic lze interpretovat pomocí Hilbertových prostorů. Například mnoho fyzikálních a technických oborů vede k takovým rovnicím a často se jako základní funkce používají řešení s konkrétními fyzikálními vlastnostmi, často ortogonální. Jako příklad z fyziky popisuje Schrödingerova rovnice závislá na čase v kvantové mechanice změnu fyzikálních vlastností v čase pomocí parciální diferenciální rovnice , jejíž řešení se nazývají vlnové funkce . Definitivní hodnoty pro fyzikální vlastnosti, jako je energie nebo hybnost, odpovídají vlastním hodnotám určitého (lineárního) diferenciálního operátoru a související vlnové funkce se nazývají vlastní stavy . Spektrální teorém rozkládá lineární kompaktní operátor působící na funkcích v rámci těchto vlastních funkcí a jejich čísel.
Algebry nad poli

Obecné vektorové prostory nemají násobení mezi vektory. Vektorový prostor vybavený dalším bilineárním operátorem definujícím násobení dvou vektorů je algebra nad polem . Mnoho algeber pochází z funkcí na nějakém geometrickém objektu: protože funkce s hodnotami v daném poli lze násobit bodově, tyto entity tvoří algebry. Věta Stone -Weierstrass například spoléhá na Banachovy algebry, které jsou jak Banachovými prostory, tak algebry.
Komutativní algebra skvěle využívá prstence polynomů v jedné nebo několika proměnných, uvedených výše . Jejich násobení je komutativní i asociativní . Tyto prstence a jejich kvocienty tvoří základ algebraické geometrie , protože jsou prstenci funkcí algebraických geometrických objektů .
Dalším zásadním příkladem jsou Lieovy algebry , které nejsou ani komutativní ani asociativní, ale jejich nesplnění je omezeno omezeními ( [ x , y ] označuje součin x a y ):
- [ x , y ] = - [ y , x ] ( anticommutativity ) a
- [ x , [ y , z ]] + [ y , [ z , x ]] + [ z , [ x , y ]] = 0 ( Jacobiho identita ).
Příklady zahrnují vektorový prostor n -by- n matice, s [ x , y ] = xy - yx je komutátor dvou matic, a R 3 , obdařen produktu kříže .
Tenzor algebry T ( V ) je formální způsob přidávání produktů kteréhokoli vektorovém prostoru V, čímž se získá algebry. Jako vektorový prostor je obklopen symboly, nazývanými jednoduché tenzory
- v 1 ⊗ v 2 ⊗ ⋯ ⊗ v n , kde se stupeň n mění.
Násobení je dáno zřetězením takových symbolů, uložením distribučního zákona pod sčítání a požadavkem, aby skalární násobení dojíždělo s tenzorovým součinem ⊗, podobně jako u tenzorového součinu dvou vektorových prostorů uvedených výše . Obecně neexistují žádné vztahy mezi v 1 ⊗ v 2 a v 2 ⊗ v 1 . Vynucení dvou takových prvků, aby byly stejné, vede k symetrické algebře , zatímco vynucení v 1 ⊗ v 2 = - v 2 ⊗ v 1 poskytne vnější algebru .
Je -li pole F výslovně uvedeno, je běžným termínem F -algebra.
Aplikace
Vektorové prostory mají mnoho aplikací, protože se často vyskytují za běžných okolností, zejména tam, kde jsou zahrnuty funkce s hodnotami v určitém poli. Poskytují rámec pro řešení analytických a geometrických problémů nebo se používají ve Fourierově transformaci. Tento seznam není vyčerpávající: existuje mnoho dalších aplikací, například v optimalizaci . Minimax věta z teorie her s uvedením existence jedinečného přínosu, když všichni hráči hrát optimálně mohou být formulovány a současně s použitím vektorové prostory metod. Teorie reprezentace úspěšně přenáší dobré porozumění lineární algebře a vektorovým prostorům do jiných matematických oblastí, jako je teorie skupin .
Distribuce
Distribuce (nebo generalizované funkce ) je lineární mapu přiřazení čísla pro každou funkci „test“ , obvykle hladké funkce s kompaktním nosičem , kontinuálním způsobem: ve výše terminologii prostor distribucí je (kontinuální) duální z testovací funkční prostor. Poslední prostor je vybaven topologií, která bere v úvahu nejen samotný f , ale také všechny jeho vyšší deriváty. Standardní příklad je výsledkem integrace testovací funkce f do nějaké domény Ω:
Když Ω = { p } , množina sestávající z jednoho bodu, redukuje se to na Diracovo rozdělení , označené δ , které spojuje s testovací funkcí f její hodnotu na p : δ ( f ) = f ( p ) . Distribuce jsou mocným nástrojem k řešení diferenciálních rovnic. Protože všechny standardní analytické pojmy, jako jsou deriváty, jsou lineární, přirozeně zasahují do prostoru distribucí. Danou rovnici je tedy možné přenést do distribučního prostoru, který je větší než podkladový funkční prostor, takže pro řešení rovnice jsou k dispozici flexibilnější metody. Například Greenovy funkce a základní řešení jsou obvykle distribucemi spíše než správnými funkcemi a lze je pak použít k nalezení řešení rovnice s předepsanými okrajovými podmínkami. Nalezené řešení pak může být v některých případech prokázáno jako skutečná funkce a řešení původní rovnice (například pomocí Lax – Milgramovy věty , důsledek Rieszovy reprezentační věty ).
Fourierova analýza
Řešení periodické funkce na součet goniometrických funkcí tvoří Fourierovu řadu , techniku velmi používanou ve fyzice a strojírenství. Podkladovým vektorovým prostorem je obvykle Hilbertův prostor L 2 (0, 2π), pro který funkce sin ( mx ) a cos ( mx ) (kde m je celé číslo) tvoří ortogonální základ. Fourierův rozvoj z L 2, funkce f je
Koeficienty m a b m se nazývají Fourierovy koeficienty z f , a jsou vypočítány pomocí vzorců
- ,
Fyzikálně vyjádřeno je funkce reprezentována jako superpozice ze sinusových vln a koeficienty poskytnout informace o funkci je frekvenční spektrum . Běžně se také používá forma Fourierovy řady komplexních čísel. Konkrétní vzorce výše jsou důsledky obecnější matematické duality zvané Pontryaginova dualita . Aplikováno na skupinu R , dává klasickou Fourierovu transformaci; aplikace ve fyzice jsou vzájemné mříže , kde základní skupina je konečný-dimenzionální skutečný vektorový prostor obdařený dodatečným vztažným bodem mřížky kódující polohy atomů v krystalech .
Fourierovy řady se používají k řešení okrajových úloh v parciálních diferenciálních rovnicích . V roce 1822 Fourier poprvé použil tuto techniku k řešení tepelné rovnice . Diskrétní verzi Fourierovy řady lze použít ve vzorkovacích aplikacích, kde je funkční hodnota známá pouze v konečném počtu stejně rozložených bodů. V tomto případě je Fourierova řada konečná a její hodnota se ve všech bodech rovná vzorkovaným hodnotám. Sada koeficientů je známá jako diskrétní Fourierova transformace (DFT) dané sekvence vzorku. DFT je jedním z klíčových nástrojů digitálního zpracování signálu , pole, jehož aplikace zahrnují radar , kódování řeči , kompresi obrazu . Formát obrázku JPEG je aplikací úzce související diskrétní kosinové transformace .
Rychlá Fourierova transformace je algoritmus pro rychlý výpočet diskrétní Fourierova transformace. Používá se nejen pro výpočet Fourierových koeficientů, ale pomocí konvoluční věty také pro výpočet konvoluce dvou konečných sekvencí. Na druhé straně jsou použity v digitálních filtrech a jako algoritmus rychlého násobení pro polynomy a velká celá čísla ( Schönhage -Strassenův algoritmus ).
Diferenciální geometrie

Tečná rovina k povrchu v bodě je přirozeně vektorový prostor, jehož počátek je shodný s bodem dotyku. Tečná rovina je nejlepší lineární aproximací nebo linearizací povrchu v bodě. Dokonce ani v trojrozměrném euklidovském prostoru obvykle neexistuje přirozený způsob, jak předepsat základ dotyčné roviny, a proto je koncipován spíše jako abstraktní vektorový prostor než skutečný souřadnicový prostor. Tečný prostor je zevšeobecňování na vyšší-rozměrné diferencovatelné variety .
Riemannian potrubí je potrubí, jehož tečné prostory jsou vybaveny vhodným vnitřním produktem . Od toho odvozený Riemannův tenzor zakřivení kóduje všechna zakřivení potrubí v jednom objektu, který nachází uplatnění například v obecné relativitě , kde Einsteinův tenzor zakřivení popisuje hmotu a energetický obsah časoprostoru . Tečnému prostoru Lieovy skupiny lze přirozeně dát strukturu Lieovy algebry a lze ji použít ke klasifikaci kompaktních Lieových skupin .
Zobecnění
Vektorové svazky
Vektor svazek je rodina vektorových prostorů kontinuálně parametrized pomocí topologické prostoru X . Přesněji řečeno, vektorový svazek nad X je topologický prostor E vybavený souvislou mapou
- π: E → X
takové, že pro každé x v X je vlákno π −1 ( x ) vektorovým prostorem. Případ dim V = 1 se nazývá svazek řádků . Pro jakýkoli vektorový prostor V činí projekce X × V → X součin X × V do „triviálního“ vektorového svazku . Vektorové svazky přes X musí být lokálně produkt X a některé (pevné) vektorový prostor V : pro každé x v X , je okolí U o x tak, že omezení na n n -1 ( U ) je izomorfní na triviální svazku U x v → U . Navzdory místně triviálnímu charakteru mohou být vektorové svazky (v závislosti na tvaru podkladového prostoru X ) ve velkém „stočeny“ (to znamená, že svazek nemusí být (globálně izomorfní) triviální svazek X × V ). Například Möbiusův pás může být viděn jako svazek čar nad kružnicí S 1 ( identifikací otevřených intervalů se skutečnou přímkou ). Liší se však od válce S 1 × R , protože druhý je orientovatelný, zatímco první nikoli.
Vlastnosti určitých vektorových svazků poskytují informace o základním topologickém prostoru. Například tangenciální svazek se skládá ze souboru tečných prostorů parametrizovaných body diferencovatelného potrubí. Tangenta svazek kruhu S 1 je celosvětově isomorphic k S 1 × R , protože tam je globální nenulová vektorové pole na S 1 . Naproti tomu podle chlupaté koule není na 2-sféře S 2 žádné (tečné) vektorové pole, které je všude nenulové. K-theory studuje třídy izomorfismu všech vektorových svazků v nějakém topologickém prostoru. Kromě prohloubení topologické a geometrické vhled, má čistě algebraické důsledky, jako je například třídění konečných-dimenzionální reálném divize algebry : R , C , na čtveřic H a octonions O .
Svazek kotangensu diferencovatelného potrubí se skládá v každém bodě potrubí z duálu tečného prostoru, kotangentního prostoru . Sekce tohoto svazku jsou známé jako diferenciální jednoformy .
Moduly
Moduly mají pro prstence to, co jsou pro pole vektorové mezery: stejné axiomy, aplikované na prstenec R místo pole F , dávají moduly. Teorie modulů, ve srovnání s teorií vektorových prostorů, je komplikována přítomností prstencových prvků, které nemají multiplikativní inverze . Moduly například nemusí mít báze, jak ukazuje Z -modul (tj. Abelianská skupina ) Z /2 Z ; ty moduly, které ano (včetně všech vektorových mezer), jsou známé jako volné moduly . Nicméně vektorový prostor lze kompaktně definovat jako modul přes prsten, což je pole , přičemž prvky se nazývají vektory. Někteří autoři používají termín vektorový prostor k označení modulů přes dělící prstenec . Algebro-geometrická interpretace komutativních prstenců prostřednictvím jejich spektra umožňuje vývoj konceptů, jako jsou lokálně volné moduly , algebraický protějšek vektorových svazků.
Afinní a projektivní prostory
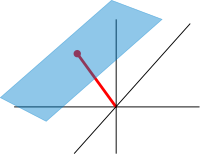
Zhruba jsou afinní mezery vektorové prostory, jejichž původ není specifikován. Přesněji řečeno, afinní prostor je množina s volnou tranzitivní vektorovou vesmírnou akcí . Zejména je vektorový prostor afinním prostorem nad sebou, podle mapy
- V × V → V , ( v , a ) ↦ a + v .
Jestliže W je vektorový prostor, pak je afinní podprostor podmnožinou W získanou překladem lineárního podprostoru V pevným vektorem x ∈ W ; tento prostor je označen x + V (to je coset z V v W ) a sestává ze všech vektorů tvaru x + V, pro v ∈ V . Důležitým příkladem je prostor řešení soustavy nehomogenních lineárních rovnic
- A x = b
zobecnění výše uvedeného homogenního případu , který lze nalézt nastavením b = 0 v této rovnici. Prostor řešení je afinní podprostor x + V , kde x je konkrétní řešení rovnice, a V je prostor řešení homogenní rovnice (dále nullspace z A ).
Množina jednorozměrných podprostorů pevného vektorového prostoru konečných rozměrů V je známá jako projektivní prostor ; může být použit k formalizaci myšlenky paralelních čar protínajících se v nekonečnu. Grassmannianové a vlajkové potrubí to zobecňují parametrizací lineárních podprostorů pevné dimenze k a příznaků podprostorů.
Viz také
- Vektor (matematika a fyzika) , seznam různých druhů vektorů
Poznámky
Citace
Reference
Algebra
- Artin, Michael (1991), Algebra , Prentice Hall , ISBN 978-0-89871-510-1
- Blass, Andreas (1984), „Existence základen implikuje axiom volby“, Axiomatická teorie množin (Boulder, Colorado, 1983) (PDF) , Contemporary Mathematics, 31 , Providence, RI: American Mathematical Society , s. 31–33 , MR 0763890
- Brown, William A. (1991), Matice a vektorové prostory , New York: M. Dekker, ISBN 978-0-8247-8419-5
- Lang, Serge (1987), Lineární algebra , Berlín, New York: Springer-Verlag , ISBN 978-0-387-96412-6
- Lang, Serge (2002), Algebra , Graduate Texts in Mathematics , 211 (Revised 3rd ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
- Mac Lane, Saunders (1999), Algebra (3. vyd.), S. 193–222, ISBN 978-0-8218-1646-2
- Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra , SIAM , ISBN 978-0-89871-454-8
- Roman, Steven (2005), Advanced Linear Algebra , Graduate Texts in Mathematics, 135 (2. vyd.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-24766-3
- Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups , CRC, ISBN 978-0-8247-9144-5
- van der Waerden, Bartel Leendert (1993), Algebra (v němčině) (9. vydání), Berlín, New York: Springer-Verlag , ISBN 978-3-540-56799-8
Analýza
- Bourbaki, Nicolas (1987), Topologické vektorové prostory , Prvky matematiky, Berlín, New York: Springer-Verlag , ISBN 978-3-540-13627-9
- Bourbaki, Nicolas (2004), Integrace I , Berlín, New York: Springer-Verlag , ISBN 978-3-540-41129-1
- Braun, Martin (1993), Diferenciální rovnice a jejich aplikace: úvod do aplikované matematiky , Berlín, New York: Springer-Verlag , ISBN 978-0-387-97894-9
- BSE-3 (2001) [1994], "Tečná rovina" , Encyklopedie matematiky , EMS Press
- Choquet, Gustave (1966), topologie , Boston, MA: Academic Press
- Dennery, Philippe; Krzywicki, Andre (1996), Matematika pro fyziky , Courier Dover Publications, ISBN 978-0-486-69193-0
- Dudley, Richard M. (1989), Skutečná analýza a pravděpodobnost , The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6
- Dunham, William (2005), The Calculus Gallery , Princeton University Press , ISBN 978-0-691-09565-3
- Evans, Lawrence C. (1998), Parciální diferenciální rovnice , Providence, RI: American Mathematical Society , ISBN 978-0-8218-0772-9
- Folland, Gerald B. (1992), Fourierova analýza a její aplikace , Brooks-Cole, ISBN 978-0-534-17094-3
- Gasquet, Claude; Witomski, Patrick (1999), Fourierova analýza a aplikace: Filtrování, numerické výpočty, vlnky , texty v aplikované matematice, New York: Springer-Verlag, ISBN 978-0-387-98485-8
- Ifeachor, Emmanuel C .; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (2nd ed.), Harlow, Essex, England: Prentice-Hall (publikováno 2002), ISBN 978-0-201-59619-9
- Krantz, Steven G. (1999), Panorama harmonické analýzy , Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
- Kreyszig, Erwin (1988), Advanced Engineering Mathematics (6. ed.), New York: John Wiley & Sons, ISBN 978-0-471-85824-9
- Kreyszig, Erwin (1989), Úvodní funkční analýza s aplikacemi , Wiley Classics Library, New York: John Wiley & Sons , ISBN 978-0-471-50459-7, MR 0992618
- Lang, Serge (1983), Skutečná analýza , Addison-Wesley , ISBN 978-0-201-14179-5
- Lang, Serge (1993), Reálná a funkční analýza , Berlín, New York: Springer-Verlag , ISBN 978-0-387-94001-4
- Loomis, Lynn H. (1953), Úvod do abstraktní harmonické analýzy , Toronto-New York – Londýn: D. Van Nostrand Company, Inc., s. X+190, hdl : 2027/uc1.b4250788
- Narici, Lawrence ; Beckenstein, Edward (2011). Topologické vektorové prostory . Čistá a aplikovaná matematika (druhé vydání.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834 .
- Schaefer, Helmut H .; Wolff, Manfred P. (1999). Topologické vektorové prostory . GTM . 8 (druhé vydání.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135 .
- Treves, François (1967), Topologické vektorové prostory, distribuce a jádra , Boston, MA: Academic Press
Historické reference
- Banach, Stefan (1922), „Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)“ (PDF) , Fundamenta Mathematicae (ve francouzštině), 3 : 133– 181, doi : 10,4064/fm-3-1-133-181 , ISSN 0016-2736
- Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Úvahy o některých aspektech elementární geometrie) (v němčině)
- Bellavitis, Giuso (1833), „Sopra alcune applicationzioni di un nuovo metodo di geometria analitica“, Il poligrafo giornale di scienze, lettre ed arti , Verona, 13 : 53–61.
- Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (ve francouzštině), Paris: Hermann
- Dorier, Jean-Luc (1995), „Obecný nástin geneze teorie vektorového prostoru“ , Historia Mathematica , 22 (3): 227–261, doi : 10,1006/hmat.1995.1024 , MR 1347828
- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (ve francouzštině), Chez Firmin Didot, père et fils
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (v němčině), O. Wigand, dotisk: Grassmann, Hermann (2000), Kannenberg, LC (ed.), The Extension Theory , přeložil Kannenberg, Lloyd C., Providence, RI: American Mathematical Society , ISBN 978-0-8218-2031-5
- Hamilton, William Rowan (1853), Přednášky o čtveřicích , Královská irská akademie
- Möbius, August Ferdinand (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentrický počet: nový nástroj pro analytické zpracování geometrie) (v němčině), archivováno z originálu 2006-11-23
- Moore, Gregory H. (1995), „Axiomatizace lineární algebry: 1875–1940“, Historia Mathematica , 22 (3): 262–303, doi : 10,1006/hmat.1995.1025
- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (v italštině), Turín
- Peano, G. (1901) Formulario mathematico : vct axioms via Internet Archive
Další reference
- Ashcroft, Neil ; Mermin, N. David (1976), Fyzika pevných látek , Toronto: Thomson Learning, ISBN 978-0-03-083993-1
- Atiyah, Michael Francis (1989), K-theory , Advanced Book Classics (2. vyd.), Addison-Wesley , ISBN 978-0-201-09394-0, MR 1043170
- Bourbaki, Nicolas (1998), Elements of Mathematics: Algebra I Chapters 1-3 , Berlin, New York: Springer-Verlag , ISBN 978-3-540-64243-5
- Bourbaki, Nicolas (1989), obecná topologie. Kapitoly 1-4 , Berlín, New York: Springer-Verlag , ISBN 978-3-540-64241-1
- Coxeter, Harold Scott MacDonald (1987), projektivní geometrie (2. vyd.), Berlín, New York: Springer-Verlag , ISBN 978-0-387-96532-1
- Eisenberg, Murray; Guy, Robert (1979), „Důkaz o chlupaté kouli“, The American Mathematical Monthly , 86 (7): 572–574, doi : 10,2307/2320587 , JSTOR 2320587
- Eisenbud, David (1995), komutativní algebra , absolventské texty z matematiky, 150 , Berlín, New York: Springer-Verlag , ISBN 978-0-387-94269-8, MR 1322960
- Goldrei, Derek (1996), The Classic Set Theory: A guided independent study (1st ed.), London: Chapman and Hall , ISBN 978-0-412-60610-6
- Griffiths, David J. (1995), Úvod do kvantové mechaniky , Upper Saddle River, New Jersey: Prentice Hall , ISBN 978-0-13-124405-4
- Halmos, Paul R. (1974), konečno-rozměrné vektorové prostory , Berlín, New York: Springer-Verlag , ISBN 978-0-387-90093-3
- Halpern, James D. (červen 1966), „Bases in Vector Spaces and the Axiom of Choice“, Proceedings of the American Mathematical Society , 17 (3): 670–673, doi : 10,2307/2035388 , JSTOR 2035388
- Hughes-Hallett, Deborah; McCallum, William G .; Gleason, Andrew M. (2013), Calculus: Single and Multivariable (6 ed.), John Wiley & Sons , ISBN 978-0470-88861-2
- Husemoller, Dale (1994), Fiber Bundles (3. vyd.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-94087-8
- Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4th ed.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-25907-7
- Kreyszig, Erwin (1991), Differential geometry , New York: Dover Publications , s. Xiv+352, ISBN 978-0-486-66721-8
- Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8. vydání), New York: John Wiley & Sons , ISBN 978-0-471-15496-9
- Luenberger, David (1997), Optimalizace metodami vektorového prostoru , New York: John Wiley & Sons , ISBN 978-0-471-18117-0
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2. vyd.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-98403-2
- Misner, Charles W .; Thorne, Kip ; Wheeler, John Archibald (1973), Gravitace , WH Freeman, ISBN 978-0-7167-0344-0
- Naber, Gregory L. (2003), Geometrie Minkowského časoprostoru , New York: Dover Publications , ISBN 978-0-486-43235-9, MR 2044239
- Schönhage, A .; Strassen, Volker (1971), „Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)“, Computing (v němčině), 7 (3–4): 281–292, doi : 10,1007/bf02242355 , ISSN 0010-485X , S2CID 9738629
- Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two) , Houston, TX: Publish or Perish
- Stewart, Ian (1975), Galoisova teorie , Chapman and Hall Mathematics Series, London: Chapman and Hall , ISBN 978-0-412-10800-6
- Varadarajan, VS (1974), Lieovy skupiny, Lieovy algebry a jejich reprezentace , Prentice Hall , ISBN 978-0-13-535732-3
- Wallace, GK (únor 1992), „Standard komprese statických obrázků JPEG“ (PDF) , IEEE Transactions on Consumer Electronics , 38 (1): xviii – xxxiv, CiteSeerX 10.1.1.318.4292 , doi : 10.1109/30.125072 , ISSN 0098 -3063 , archivováno z originálu (PDF) dne 2007-01-13 , vyvoláno 2017-10-25
- Weibel, Charles A. (1994). Úvod do homologické algebry . Cambridgeská studia v pokročilé matematice. 38 . Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324 . OCLC 36131259 .
externí odkazy
- "Vektorový prostor" , Encyklopedie matematiky , EMS Press , 2001 [1994]













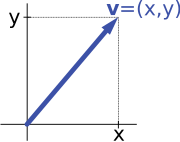






















































![{\ frac {a_ {0}} {2}}+\ sum _ {m = 1}^{\ infty} \ left [a_ {m} \ cos \ left (mx \ right)+b_ {m} \ sin \ left (mx \ right) \ right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b02fb26ebada4babaa1d88e20bb63e3b370c13b3)


