Autoregresní model - Autoregressive model

Ve statistikách, ekonometrii a zpracování signálu je autoregresivní ( AR ) model reprezentací typu náhodného procesu; jako takový se používá k popisu určitých časově proměnných procesů v přírodě, ekonomii atd. Autoregresní model určuje, že výstupní proměnná závisí lineárně na vlastních předchozích hodnotách a na stochastickém termínu (nedokonale předvídatelném členu); model je tedy ve formě stochastické diferenciální rovnice (nebo relačního vztahu, který by neměl být zaměňován s diferenciální rovnicí). Spolu s modelem klouzavého průměru (MA) je to speciální případ a klíčová součást obecnějších modelů autoregresivního – klouzavého průměru (ARMA) a autoregresních integrovaných klouzavých průměrů (ARIMA) časových řad, které mají složitější stochastické struktura; je to také speciální případ vektorového autoregresivního modelu (VAR), který se skládá ze systému více než jedné do sebe zapadající stochastické rozdílové rovnice ve více než jedné vyvíjející se náhodné proměnné.

Na rozdíl od modelu s klouzavým průměrem (MA) není autoregresní model vždy stacionární, protože může obsahovat jednotkový kořen.

Definice

Zápis označuje autoregresivní model řádu p . Model AR ( p ) je definován jako ${\ displaystyle AR (p)}$

${\ Displaystyle X_ {t} = c+\ sum _ {i = 1}^{p} \ varphi _ {i} X_ {ti}+\ varepsilon _ {t} \,}$

kde jsou parametry modelu, je konstanta a je bílý šum . To lze ekvivalentně zapsat pomocí operátoru zpětného řazení B as ${\ Displaystyle \ varphi _ {1}, \ ldots, \ varphi _ {p}}$${\ displaystyle c}$${\ displaystyle \ varepsilon _ {t}}$

${\ Displaystyle X_ {t} = c+\ sum _ {i = 1}^{p} \ varphi _ {i} B^{i} X_ {t}+\ varepsilon _ {t}}$

takže pohybem součtového členu na levou stranu a pomocí polynomického zápisu máme

${\ Displaystyle \ phi [B] X_ {t} = c+\ varepsilon _ {t} \ ,.}$

Autoregresního model může tedy být považován za výstup s all- pólového nekonečnou impulzní odezvy filtru, jehož vstup je bílý šum.

Aby model zůstal nehybný v širokém smyslu, jsou nutná určitá omezení parametrů . Například procesy v modelu AR (1) s nejsou stacionární. Obecněji řečeno, aby byl model AR ( p ) stacionární v širokém smyslu, musí kořeny polynomu ležet mimo jednotkový kruh , tj. Každý (komplexní) kořen musí splňovat (viz strany 88,90). ${\ Displaystyle | \ varphi _ {1} | \ geq 1}$${\ Displaystyle \ Phi (z): = \ textstyle 1- \ sum _ {i = 1}^{p} \ varphi _ {i} z^{pi}}$${\ displaystyle z_ {i}}$${\ displaystyle | z_ {i} |> 1}$

Intertemporal effect of shocks

V procesu AR ovlivňuje jednorázový šok hodnoty vyvíjející se proměnné nekonečně daleko do budoucnosti. Zvažte například model AR (1) . Nenulová hodnota pro řekněme čas t = 1 ovlivňuje částkou . Pak podle rovnice AR pro, pokud jde o , to ovlivňuje částkou . Pak podle rovnice AR pro, pokud jde o , to ovlivňuje částkou . Pokračování v tomto procesu ukazuje, že účinek nikdy nekončí, ačkoli pokud je proces nehybný, účinek se v limitu zmenšuje směrem k nule. ${\ Displaystyle X_ {t} = c+\ varphi _ {1} X_ {t-1}+\ varepsilon _ {t}}$${\ displaystyle \ varepsilon _ {t}}$${\ displaystyle X_ {1}}$${\ displaystyle \ varepsilon _ {1}}$${\ displaystyle X_ {2}}$${\ displaystyle X_ {1}}$${\ displaystyle X_ {2}}$${\ Displaystyle \ varphi _ {1} \ varepsilon _ {1}}$${\ displaystyle X_ {3}}$${\ displaystyle X_ {2}}$${\ displaystyle X_ {3}}$${\ Displaystyle \ varphi _ {1}^{2} \ varepsilon _ {1}}$${\ displaystyle \ varepsilon _ {1}}$

Protože každý šok ovlivňuje hodnoty X nekonečně daleko do budoucnosti, než k nim dojde, jakákoli daná hodnota X _t je ovlivněna šoky, které se vyskytují nekonečně daleko do minulosti. To je také vidět přepsáním autoregrese

${\ Displaystyle \ phi (B) X_ {t} = \ varepsilon _ {t} \,}$

(kde byl konstantní člen potlačen za předpokladu, že proměnná byla měřena jako odchylky od jejího průměru) jako

${\ displaystyle X_ {t} = {\ frac {1} {\ phi (B)}} \ varepsilon _ {t} \ ,.}$

Když je provedeno dělení polynomu na pravé straně, polynom v operátoru zpětného posunu, na který se vztahuje, má nekonečné pořadí - to znamená, že na pravé straně rovnice se objeví nekonečný počet zpožděných hodnot . ${\ displaystyle \ varepsilon _ {t}}$${\ displaystyle \ varepsilon _ {t}}$

Charakteristický polynom

Funkce autokorelace procesu AR ( p ) může být vyjádřena jako

${\ Displaystyle \ rho (\ tau) = \ sum _ {k = 1}^{p} a_ {k} y_ {k}^{-| \ tau |},}$

kde jsou kořeny polynomu ${\ displaystyle y_ {k}}$

${\ Displaystyle \ phi (B) = 1- \ sum _ {k = 1}^{p} \ varphi _ {k} B^{k}}$

kde B je operátor zpětného posunu , kde je funkce definující autoregrese a kde jsou koeficienty v automatické regresi. ${\ displaystyle \ phi (\ cdot)}$${\ displaystyle \ varphi _ {k}}$

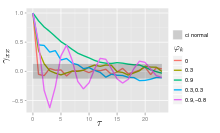
Funkce autokorelace procesu AR ( p ) je součtem rozpadajících se exponenciálů.

• Každý skutečný kořen přispívá k funkci autokorelace, která se exponenciálně rozpadá.
• Podobně každý pár komplexních kořenů konjugátu přispívá exponenciálně tlumenou oscilací.

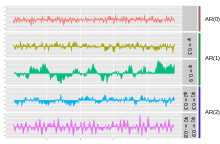
Grafy procesů AR ( p )

Nejjednodušším procesem AR je AR (0), který mezi podmínkami není nijak závislý. K výstupu procesu přispívá pouze termín chyba/inovace/šum, takže na obrázku odpovídá AR (0) bílému šumu.

U procesu AR (1) s kladem přispívá k výstupu pouze předchozí člen procesu a hlukový člen. Pokud se blíží 0, pak proces stále vypadá jako bílý šum, ale jak se blíží k 1, výstup získá větší příspěvek z předchozího termínu vzhledem k šumu. Výsledkem je „vyhlazení“ nebo integrace výstupu, podobně jako dolní propust. ${\ Displaystyle \ varphi}$${\ Displaystyle \ varphi}$${\ Displaystyle \ varphi}$

U procesu AR (2) přispívají k výstupu předchozí dva termíny a termín šumu. Pokud jsou obě a kladné, bude výstup připomínat dolní propust se sníženou vysokofrekvenční částí šumu. Pokud je kladný, zatímco je záporný, pak proces upřednostňuje změny znaménka mezi podmínkami procesu. Výstup osciluje. To lze přirovnat k detekci hran nebo detekci změny směru. ${\ displaystyle \ varphi _ {1}}$${\ displaystyle \ varphi _ {2}}$${\ displaystyle \ varphi _ {1}}$${\ displaystyle \ varphi _ {2}}$

Příklad: Proces AR (1)

Proces AR (1) je dán:

${\ Displaystyle X_ {t} = c+\ varphi X_ {t-1}+\ varepsilon _ {t} \,}$

kde je proces bílého šumu s nulovým průměrem a konstantním rozptylem . (Poznámka: Dolní index byl vypuštěn.) Proces je nehybný, pokud je získán jako výstup stabilního filtru, jehož vstupem je bílý šum. (Je-li pak rozptyl závisí na zpožděním t, aby se rozptyl série rozchází do nekonečna t jde do nekonečna, a proto není širokém smyslu pohybu.) Za předpokladu, že je střední je shodný pro všechny hodnoty t ukládané samotná definice široké smyslové stacionarity. Pokud je průměr označen , vyplývá z ${\ displaystyle \ varepsilon _ {t}}$${\ Displaystyle \ sigma _ {\ varepsilon}^{2}}$${\ displaystyle \ varphi _ {1}}$${\ Displaystyle | \ varphi | <1}$${\ Displaystyle \ varphi = 1}$${\ displaystyle X_ {t}}$${\ Displaystyle | \ varphi | <1}$${\ displaystyle \ operatorname {E} (X_ {t})}$${\ Displaystyle \ mu}$

${\ displaystyle \ operatorname {E} (X_ {t}) = \ operatorname {E} (c)+\ varphi \ operatorname {E} (X_ {t-1})+\ operatorname {E} (\ varepsilon _ { t}),}$

že

${\ Displaystyle \ mu = c +\ varphi \ mu +0,}$

a proto

${\ Displaystyle \ mu = {\ frac {c} {1- \ varphi}}.}$

Zejména pokud , pak průměr je 0. ${\ displaystyle c = 0}$

Rozptyl je

${\ displaystyle {\ textrm {var}} (X_ {t}) = \ operatorname {E} (X_ {t} ^{2})-\ mu ^{2} = {\ frac {\ sigma _ {\ varepsilon } ^{2}} {1- \ varphi ^{2}}},}$

kde je standardní odchylka . To lze ukázat tím, že si toho všimneme ${\ displaystyle \ sigma _ {\ varepsilon}}$${\ displaystyle \ varepsilon _ {t}}$

${\ Displaystyle {\ textrm {var}} (X_ {t}) = \ varphi ^{2} {\ textrm {var}} (X_ {t-1})+\ sigma _ {\ varepsilon} ^{2} ,}$

a poté tím, že si všimneme, že výše uvedené množství je stabilním pevným bodem tohoto vztahu.

Autokovarianční je dán

${\ Displaystyle B_ {n} = \ operatorname {E} (X_ {t+n} X_ {t})-\ mu ^{2} = {\ frac {\ sigma _ {\ varepsilon} ^{2}} { 1- \ varphi ^{2}}} \, \, \ varphi ^{| n |}.}$

Je vidět, že funkce autocovariance se rozpadá s časem rozpadu (také nazývaným časová konstanta ) [aby to bylo vidět, napište, kde je nezávislý na . Pak si toho všimněte a přiřaďte to k zákonu exponenciálního rozpadu ]. ${\ Displaystyle \ tau = -1/\ ln (\ varphi)}$${\ Displaystyle B_ {n} = K \ varphi ^{| n |}}$${\ displaystyle K}$${\ displaystyle n}$${\ Displaystyle \ varphi ^{| n |} = e ^{| n | \ ln \ varphi}}$${\ displaystyle e^{-n/\ tau}}$

Funkce spektrální hustoty je Fourierova transformace funkce autokoviance. V diskrétních termínech to bude diskrétní Fourierova transformace:

${\ Displaystyle \ Phi (\ omega) = {\ frac {1} {\ sqrt {2 \ pi}}} \, \ sum _ {n =-\ infty}^{\ infty} B_ {n} e^{ -i \ omega n} = {\ frac {1} {\ sqrt {2 \ pi}}} \, \ left ({\ frac {\ sigma _ {\ varepsilon} ^{2}} {1+ \ varphi ^ {2} -2 \ varphi \ cos (\ omega)}} \ right).}$

Tento výraz je periodický kvůli diskrétní povaze , která se ve jmenovateli projevuje jako kosinový výraz. Pokud předpokládáme, že doba vzorkování ( ) je mnohem menší než doba rozpadu ( ), pak můžeme použít aproximaci kontinua k : ${\ displaystyle X_ {j}}$${\ Displaystyle \ Delta t = 1}$${\ displaystyle \ tau}$${\ displaystyle B_ {n}}$

${\ Displaystyle B (t) \ zhruba {\ frac {\ sigma _ {\ varepsilon} ^{2}} {1- \ varphi ^{2}}} \, \, \ varphi ^{| t |}}$

který poskytuje Lorentzianův profil pro spektrální hustotu:

${\ Displaystyle \ Phi (\ omega) = {\ frac {1} {\ sqrt {2 \ pi}}} \, {\ frac {\ sigma _ {\ varepsilon} ^{2}} {1- \ varphi ^ {2}}} \, {\ frac {\ gamma} {\ pi (\ gamma ^{2}+\ omega ^{2})}}}$

kde je úhlová frekvence spojená s dobou rozpadu . ${\ displaystyle \ gamma = 1/\ tau}$${\ displaystyle \ tau}$

Alternativní výraz pro lze odvodit nejprve nahrazením za v definující rovnici. Pokračováním tohoto procesu se N krát získá ${\ displaystyle X_ {t}}$${\ Displaystyle c+\ varphi X_ {t-2}+\ varepsilon _ {t-1}}$${\ displaystyle X_ {t-1}}$

${\ Displaystyle X_ {t} = c \ sum _ {k = 0} ^{N-1} \ varphi ^{k}+\ varphi ^{N} X_ {tN}+\ sum _ {k = 0} ^ {N-1} \ varphi ^{k} \ varepsilon _ {tk}.}$

Pro N blížící se nekonečnu se přiblíží k nule a: ${\ displaystyle \ varphi ^{N}}$

${\ Displaystyle X_ {t} = {\ frac {c} {1- \ varphi}}+\ sum _ {k = 0} ^{\ infty} \ varphi ^{k} \ varepsilon _ {tk}.}$

Je vidět, že je to bílý šum spletený s jádrem plus konstantní průměr. V případě, že bílý šum je Gaussian proces pak je také Gaussian proces. V ostatních případech centrální limitní věta naznačuje, že bude přibližně normálně distribuováno, když je blízko jedné. ${\ displaystyle X_ {t}}$${\ Displaystyle \ varphi ^{k}}$${\ displaystyle \ varepsilon _ {t}}$${\ displaystyle X_ {t}}$${\ displaystyle X_ {t}}$${\ Displaystyle \ varphi}$

Explicitní průměr/rozdíl procesu AR (1)

Model AR (1) je diskrétní časovou analogií spojitého Ornstein-Uhlenbeckova procesu . Někdy je proto užitečné porozumět vlastnostem modelu AR (1) obsazeného v ekvivalentní podobě. V této podobě je model AR (1) s parametrem procesu dán vztahem: ${\ displaystyle \ theta}$

${\ Displaystyle X_ {t+1} = X_ {t}+(1- \ theta) (\ mu -X_ {t})+\ epsilon _ {t+1}}$, kde a je model průměr.${\ Displaystyle | \ theta | <1 \,}$${\ Displaystyle \ mu}$

Tím, že to vložíte do formuláře a poté rozšíříte sérii pro , můžete ukázat, že: ${\ Displaystyle X_ {t+1} = c+\ phi X_ {t} \+\ epsilon _ {t+1}}$${\ displaystyle X_ {t+n}}$

${\ displaystyle \ operatorname {E} (X_ {t+n} | X_ {t}) = \ mu \ left [1- \ theta ^{n} \ right]+X_ {t} \ theta ^{n}}$, a

${\ displaystyle \ operatorname {Var} (X_ {t+n} | X_ {t}) = \ sigma ^{2} {\ frac {1- \ theta ^{2n}} {1- \ theta ^{2} }}}$.

Volba maximálního zpoždění

Částečná autokorelace procesu AR (p) se rovná nule při zpoždění, které není větší než řád p a poskytuje dobrý model pro korelaci mezi a , takže příslušné maximální zpoždění je takové, za kterým jsou částečné autokorelace nulové. ${\ displaystyle X_ {1}}$${\ displaystyle X_ {p+1}}$

Výpočet parametrů AR

Existuje mnoho způsobů, jak odhadnout koeficienty, například obyčejný postup nejmenších čtverců nebo metoda momentů (prostřednictvím Yule -Walkerových rovnic).

Model AR ( p ) je dán rovnicí

${\ Displaystyle X_ {t} = \ sum _ {i = 1}^{p} \ varphi _ {i} X_ {ti}+\ varepsilon _ {t}. \,}$

Je založen na parametrech, kde i = 1, ..., s . Mezi těmito parametry a kovarianční funkcí procesu existuje přímá shoda a tuto korespondenci je možné převrátit za účelem určení parametrů z autokorelační funkce (která je sama získána z kovariancí). To se provádí pomocí Yule -Walkerových rovnic. ${\ displaystyle \ varphi _ {i}}$

Yule -Walkerovy rovnice

Rovnice Yule -Walker , pojmenované pro Udny Yule a Gilberta Walkera , jsou následující sadou rovnic.

${\ Displaystyle \ gamma _ {m} = \ sum _ {k = 1}^{p} \ varphi _ {k} \ gamma _ {mk}+\ sigma _ {\ varepsilon}^{2} \ delta _ { m, 0},}$

kde m  = 0,…,  p , čímž se získají rovnice p  + 1 . Zde je funkce autokoviance X _t , je standardní odchylkou procesu vstupního šumu a je funkcí Kroneckerova delta . ${\ displaystyle \ gamma _ {m}}$${\ displaystyle \ sigma _ {\ varepsilon}}$${\ Displaystyle \ delta _ {m, 0}}$

Protože poslední část individuální rovnice je nenulová, pouze pokud m  = 0 , sadu rovnic lze vyřešit reprezentací rovnic pro m  > 0 ve formě matice, čímž dostaneme rovnici

${\ Displaystyle {\ begin {bmatrix} \ gamma _ {1} \\\ gamma _ {2} \\\ gamma _ {3} \\\ vdots \\\ gamma _ {p} \\\ end {bmatrix} } = {\ begin {bmatrix} \ gamma _ {0} & \ gamma _ {-1} & \ gamma _ {-2} & \ cdots \\\ gamma _ {1} & \ gamma _ {0} & \ gamma _ {-1} & \ cdots \\\ gamma _ {2} & \ gamma _ {1} & \ gamma _ {0} & \ cdots \\\ vdots & \ vdots & \ vdots & \ ddots \\\ gamma _ {p-1} & \ gamma _ {p-2} & \ gamma _ {p-3} & \ cdots \\\ end {bmatrix}} {\ begin {bmatrix} \ varphi _ {1} \\ \ varphi _ {2} \\\ varphi _ {3} \\\ vdots \\\ varphi _ {p} \\\ end {bmatrix}}}$

což lze vyřešit pro všechny Zbývající rovnice pro m = 0 je ${\ Displaystyle \ {\ varphi _ {m}; m = 1,2, \ tečky, p \}.}$

${\ Displaystyle \ gamma _ {0} = \ sum _ {k = 1}^{p} \ varphi _ {k} \ gamma _ {-k}+\ sigma _ {\ varepsilon}^{2},}$

které, jakmile jsou známy, lze vyřešit${\ Displaystyle \ {\ varphi _ {m}; m = 1,2, \ tečky, p \}}$${\ Displaystyle \ sigma _ {\ varepsilon}^{2}.}$

Alternativní formulace je z hlediska autokorelační funkce . Parametry AR jsou určeny prvními prvky p +1 funkce autokorelace. Plnou autokorelační funkci pak lze odvodit rekurzivním výpočtem ${\ Displaystyle \ rho (\ tau)}$

${\ Displaystyle \ rho (\ tau) = \ sum _ {k = 1}^{p} \ varphi _ {k} \ rho (k- \ tau)}$

Příklady některých procesů AR ( p ) nižšího řádu

• p = 1
  • ${\ displaystyle \ gamma _ {1} = \ varphi _ {1} \ gamma _ {0}}$
  • Proto ${\ Displaystyle \ rho _ {1} = \ gamma _ {1}/\ gamma _ {0} = \ varphi _ {1}}$
• p = 2
  • Yule -Walkerovy rovnice pro proces AR (2) jsou

    ${\ Displaystyle \ gamma _ {1} = \ varphi _ {1} \ gamma _ {0}+\ varphi _ {2} \ gamma _ {-1}}$

    ${\ Displaystyle \ gamma _ {2} = \ varphi _ {1} \ gamma _ {1}+\ varphi _ {2} \ gamma _ {0}}$

    • Pamatuj si to ${\ Displaystyle \ gamma _ {-k} = \ gamma _ {k}}$
    • Pomocí výtěžků první rovnice ${\ Displaystyle \ rho _ {1} = \ gamma _ {1}/\ gamma _ {0} = {\ frac {\ varphi _ {1}} {1- \ varphi _ {2}}}}$
    • Pomocí výtěžku rekurzního vzorce ${\ Displaystyle \ rho _ {2} = \ gamma _ {2}/\ gamma _ {0} = {\ frac {\ varphi _ {1}^{2}-\ varphi _ {2}^{2}+ \ varphi _ {2}} {1- \ varphi _ {2}}}}$

Odhad parametrů AR

Výše uvedené rovnice (Yule -Walkerovy rovnice) poskytují několik cest k odhadu parametrů modelu AR ( p ) nahrazením teoretických kovariancí odhadovanými hodnotami. Některé z těchto variant lze popsat následovně:

• Odhad autocovariancí nebo autokorelací. Zde se každý z těchto výrazů odhaduje samostatně pomocí konvenčních odhadů. Existují různé způsoby, jak toho dosáhnout, a volba mezi nimi ovlivňuje vlastnosti odhadovacího schématu. Některé volby mohou například vytvářet negativní odhady rozptylu.
• Formulace jako regresní problém nejmenších čtverců, ve kterém je konstruován obyčejný problém predikce nejmenších čtverců, založený na predikci hodnot X _t na p předchozích hodnotách stejné řady. To lze považovat za schéma předpovědi vpřed. V normální rovnice tohoto problému je možné vidět, aby odpovídaly aproximaci maticovém tvaru rovnic Yule-Walker, ve kterém je každý výskyt z autokovarianční stejného zpoždění nahrazen mírně odlišným odhadu.
• Formulace jako rozšířená forma obyčejného problému predikce nejmenších čtverců. Zde jsou dvě sady predikčních rovnic sloučeny do jednoho odhadovacího schématu a jedné sady normálních rovnic. Jedna sada je sada rovnic předpovědi vpřed a druhá je odpovídající sadou rovnic zpětné predikce, které se týkají zpětné reprezentace modelu AR:

${\ Displaystyle X_ {t} = c+\ sum _ {i = 1}^{p} \ varphi _ {i} X_ {ti}+\ varepsilon _ {t}^{*} \ ,.}$

Zde by predikované hodnoty X _t vycházely z p budoucích hodnot stejné řady. Tento způsob odhadu parametrů AR je způsoben Burgem a nazývá se Burgova metoda: Burg a novější autoři nazývali tyto konkrétní odhady „odhady maximální entropie“, ale zdůvodnění za tím platí pro použití jakékoli sady odhadovaných parametrů AR. Ve srovnání se schématem odhadu používajícím pouze rovnice předpovědi vpřed jsou vytvářeny různé odhady autocovariancí a odhady mají různé vlastnosti stability. Burg odhady jsou zvláště spojené s maximálním entropickým spektrálním odhadem .

Mezi další možné přístupy k odhadu patří odhad maximální pravděpodobnosti . K dispozici jsou dvě odlišné varianty maximální pravděpodobnosti: v jedné (široce ekvivalentní schématu nejmenších čtverců s dopřednou predikcí) je uvažována funkce pravděpodobnosti, která odpovídá podmíněné distribuci pozdějších hodnot v řadě vzhledem k počátečním hodnotám p v řadě; ve druhém uvažovaná funkce pravděpodobnosti je ta, která odpovídá bezpodmínečnému společnému rozdělení všech hodnot v sledované řadě. K podstatným rozdílům ve výsledcích těchto přístupů může dojít, pokud je sledovaná řada krátká, nebo pokud se proces blíží nestacionaritě.

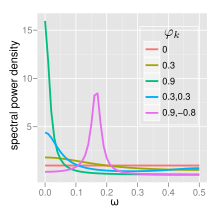
Spektrum

Spektrální hustota výkonu (PSD) z (AR p ) procesu se rozptylu šumu je ${\ Displaystyle \ mathrm {Var} (Z_ {t}) = \ sigma _ {Z}^{2}}$

${\ Displaystyle S (f) = {\ frac {\ sigma _ {Z}^{2}} {| 1- \ sum _ {k = 1}^{p} \ varphi _ {k} e^{-i2 \ pi fk} |^{2}}}.}$

AR (0)

Pro bílý šum (AR (0))

${\ Displaystyle S (f) = \ sigma _ {Z}^{2}.}$

AR (1)

Pro AR (1)

${\ Displaystyle S (f) = {\ frac {\ sigma _ {Z}^{2}} {| 1- \ varphi _ {1} e^{-2 \ pi if} |^{2}}} = {\ frac {\ sigma _ {Z}^{2}} {1+ \ varphi _ {1}^{2} -2 \ varphi _ {1} \ cos 2 \ pi f}}}$

• Pokud existuje jeden spektrální vrchol při f = 0, často označovaný jako červený šum . Jak se blíží 1, je silnější výkon na nízkých frekvencích, tj. Větší časové zpoždění. Jedná se pak o nízkoprůchodový filtr, při aplikaci na světlo celého spektra bude filtrováno vše kromě červeného světla.${\ Displaystyle \ varphi _ {1}> 0}$${\ displaystyle \ varphi _ {1}}$
• Pokud existuje minimum při f = 0, často označované jako modrý šum . Podobně to funguje jako horní propust, filtrováno bude vše kromě modrého světla.${\ Displaystyle \ varphi _ {1} <0}$

AR (2)

Procesy AR (2) lze rozdělit do tří skupin v závislosti na charakteristikách jejich kořenů:

${\ Displaystyle z_ {1}, z_ {2} = {\ frac {1} {2}} \ left (\ varphi _ {1} \ pm {\ sqrt {\ varphi _ {1}^{2} +4 \ varphi _ {2}}} \ right)}$

• Když má tento proces dvojici komplexně sdružených kořenů, vytváří vrchol střední frekvence při:${\ Displaystyle \ varphi _ {1}^{2} +4 \ varphi _ {2} <0}$

${\ Displaystyle f ^{*} = {\ frac {1} {2 \ pi}} \ cos ^{-1} \ left ({\ frac {\ varphi _ {1} (\ varphi _ {2} -1 )} {4 \ varphi _ {2}}} \ right)}$

Jinak má tento proces skutečné kořeny a:

• Když funguje jako dolní propust na bílý šum se spektrálním vrcholem při${\ Displaystyle \ varphi _ {1}> 0}$${\ displaystyle f = 0}$
• Když funguje jako horní propust na bílý šum se spektrálním vrcholem při .${\ Displaystyle \ varphi _ {1} <0}$${\ displaystyle f = 1/2}$

Proces je nestacionární, když jsou kořeny mimo jednotkový kruh. Tento proces je stabilní, když jsou kořeny v jednotkovém kruhu, nebo ekvivalentně, když jsou koeficienty v trojúhelníku . ${\ Displaystyle -1 \ leq \ varphi _ {2} \ leq 1- | \ varphi _ {1} |}$

Plnou funkci PSD lze vyjádřit ve skutečné podobě jako:

${\ Displaystyle S (f) = {\ frac {\ sigma _ {Z}^{2}} {1+ \ varphi _ {1}^{2}+\ varphi _ {2}^{2} -2 \ varphi _ {1} (1- \ varphi _ {2}) \ cos (2 \ pi f) -2 \ varphi _ {2} \ cos (4 \ pi f)}}}$

Implementace v balíčcích statistik

• R , balíček statistik obsahuje funkci ar .
• Nástroje MATLAB Econometrics Toolbox a System Identification Toolbox obsahují autoregresivní modely
• Matlab a Octave : Sada nástrojů TSA obsahuje několik funkcí odhadu pro jednovariantní, vícerozměrné a adaptivní autoregresivní modely.
• PyMC3 : bayesianského statistika a pravděpodobnostní programový rámec podpěry autoregresní režimy s p zaostává.
• bayesloop podporuje odvozování parametrů a výběr modelu pro proces AR-1 s časově proměnnými parametry.
• Python : implementace ve statistických modelech.

Impulsní reakce

Impulsní odezva systému je změna ve vyvíjejícím se měnit v odezvě na změnu hodnoty šok období k- období dříve, jako funkce k . Protože model AR je zvláštním případem vektorového autoregresivního modelu, platí zde výpočet impulzní odezvy ve vektorové autoregresní#impulzní odpovědi .

n -krokové předpovídání

Jednou parametry autoregrese

${\ Displaystyle X_ {t} = c+\ sum _ {i = 1}^{p} \ varphi _ {i} X_ {ti}+\ varepsilon _ {t} \,}$

byly odhadnuty, autoregrese může být použita k předpovědi libovolného počtu období do budoucnosti. První použití t se vztahuje k prvnímu období, pro které ještě nejsou data k dispozici; dosadit známé předchozí hodnoty X _t-i za i = 1, ..., p do autoregresivní rovnice při nastavení chybového členu na nulu (protože předpovídáme, že X _t se rovná jeho očekávané hodnotě a očekávané hodnotě nepozorovaného chybového členu je nula). Výstupem autoregresivní rovnice je předpověď pro první nepozorované období. Dále použijte t k označení dalšího období, pro které ještě nejsou data k dispozici; k předpovědi se opět používá autoregresivní rovnice s jedním rozdílem: hodnota X jednoho období před tím, které je nyní předpovídáno, není známa, takže se místo toho použije jeho očekávaná hodnota - předpokládaná hodnota vyplývající z předchozího kroku prognózy - . Pak se pro budoucí období použije stejný postup, pokaždé s použitím jedné další předpovědní hodnoty na pravé straně prediktivní rovnice, dokud po p predikcích nebudou všechny hodnoty p pravé strany předpovězeny z předchozích kroků. ${\ displaystyle \ varepsilon _ {t}}$

Existují čtyři zdroje nejistoty ohledně předpovědí získaných tímto způsobem: (1) nejistota, zda je autoregresní model správným modelem; (2) nejistota ohledně přesnosti předpovídaných hodnot, které jsou použity jako zpožděné hodnoty na pravé straně autoregresivní rovnice; (3) nejistota ohledně skutečných hodnot autoregresivních koeficientů; a (4) nejistota ohledně hodnoty chybového termínu pro předpovídané období. Každá z posledních tří lze kvantifikovat a spojí na interval spolehlivosti pro n -Step napřed předpovědi; interval spolehlivosti se bude rozšiřovat, protože n se bude zvyšovat, protože se použije rostoucí počet odhadovaných hodnot pro proměnné na pravé straně. ${\ displaystyle \ varepsilon _ {t} \,}$

Hodnocení kvality prognóz

Prediktivní výkon autoregresivního modelu lze posoudit, jakmile byl proveden odhad, pokud je použita křížová validace . V tomto přístupu byla některá původně dostupná data použita pro účely odhadu parametrů a část (z dostupných pozorování později v datové sadě) byla zadržena pro testování mimo vzorek. Alternativně po uplynutí určité doby po provedení odhadu parametrů bude k dispozici více dat a bude možné vyhodnotit prediktivní výkon a poté použít nová data.

V každém případě existují dva aspekty prediktivního výkonu, které lze vyhodnotit: výkon o jeden krok vpřed a n -krok vpřed. Pro jednokrokový výkon vpřed jsou odhadované parametry použity v autoregresivní rovnici spolu s pozorovanými hodnotami X pro všechna období před tím, které je předpovídáno, a výstupem rovnice je jednostupňová předpověď; tento postup se používá k získání předpovědí pro každé pozorování mimo vzorek. K vyhodnocení kvality n -krokových předpovědí se k získání predikcí používá postup předpovídání v předchozí části.

Vzhledem k sadě predikovaných hodnot a odpovídající sadě skutečných hodnot pro X pro různá časová období je běžnou vyhodnocovací technikou použití střední kvadratické predikční chyby ; jsou k dispozici i další opatření (viz předpovědi#přesnost předpovědí ).

Nabízí se otázka, jak interpretovat naměřenou přesnost předpovědí - například, co je „vysoká“ (špatná) nebo „nízká“ (dobrá) hodnota střední chyby predikce na druhou? Existují dva možné body srovnání. Za prvé, pro účely srovnání lze použít předpovědní přesnost alternativního modelu, odhadovanou podle různých předpokladů modelování nebo různých odhadovacích technik. Za druhé, míru přesnosti mimo vzorek lze porovnat se stejným měřítkem vypočítaným pro datové body ve vzorku (které byly použity pro odhad parametrů), pro které je k dispozici dostatek předchozích hodnot dat (tj. Vynechání prvních p dat body, pro které p předchozí datové body nejsou k dispozici). Vzhledem k tomu, že model byl specificky odhadnut tak, aby co nejlépe odpovídal bodům ve vzorku, bude obvykle platit, že prediktivní výkon mimo vzorek bude horší než prediktivní výkon ve vzorku. Pokud se ale prediktivní kvalita zhorší mimo vzorek „ne moc“ (což není přesně definovatelné), pak může být prognostik s výkonem spokojen.

Viz také

• Klouzavý průměrný model
• Lineární diferenční rovnice
• Prediktivní analýza
• Lineární prediktivní kódování
• Rezonance
• Levinsonova rekurze
• Ornstein – Uhlenbeckův proces

Poznámky

Reference

• Mills, Terence C. (1990). Techniky časové řady pro ekonomy . Cambridge University Press.
• Percival, Donald B .; Walden, Andrew T. (1993). Spektrální analýza pro fyzické aplikace . Cambridge University Press.
• Pandit, Sudhakar M .; Wu, Shien-Ming (1983). Časová řada a systémová analýza s aplikacemi . John Wiley & Sons.

externí odkazy

• AutoRegresní analýza (AR) od Paula Bourkeho
• Přednáška ekonometrie (téma: Autoregresivní modely) na YouTube od Marka Thomy