Berry – Esseenova věta - Berry–Esseen theorem

V teorii pravděpodobnosti je centrální limitní věta uvádí, že za určitých okolností je rozdělení pravděpodobnosti z zmenšen průměr náhodného vzorku konverguje k normálnímu rozdělení , jak se zvětšuje velikost vzorku do nekonečna. Za silnějších předpokladů dává Berry-Esseenova věta nebo Berry-Esseenova nerovnost kvantitativnější výsledek, protože také specifikuje rychlost, s jakou k této konvergenci dochází, tím, že stanoví vazbu na maximální chybu aproximace mezi normálním rozdělením a skutečné rozdělení střední velikosti měřítka. Aproximace se měří vzdáleností Kolmogorov – Smirnov . V případě nezávislých vzorků je míra konvergence n ^−1/2 , kde n je velikost vzorku a konstanta se odhaduje z hlediska třetích absolutních normalizovaných momentů .

Výrok věty

Výroky věty se liší, protože to nezávisle objevili dva matematici , Andrew C. Berry (v roce 1941) a Carl-Gustav Esseen (1942), kteří jej poté spolu s dalšími autory během následujících desetiletí opakovaně vylepšovali.

Stejně rozdělené sčítání

Jedna verze, která kvůli jasnosti poněkud obětuje obecnost, je následující:

Existuje kladná konstanta C taková, že pokud X ₁ , X ₂ , ..., jsou iid náhodné proměnné s E ( X ₁ ) = 0, E ( X ₁ ² ) = σ ² > 0 a E (| X ₁ | ³ ) = ρ <∞, a pokud definujeme

${\ displaystyle Y_ {n} = {X_ {1} + X_ {2} + \ cdots + X_ {n} \ přes n}}$

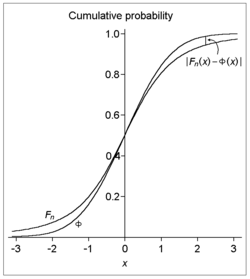
vzorek střední , s F _n na kumulativní distribuční funkce z

${\ displaystyle {Y_ {n} {\ sqrt {n}} \ přes {\ sigma}},}$

a Φ kumulativní distribuční funkce standardního normálního rozdělení , pak pro všechna x a n ,

${\ displaystyle \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq {C \ rho \ over \ sigma ^ {3} {\ sqrt {n}}}. \ \ \ \ ( 1)}$

Ilustrace rozdílu v kumulativních distribučních funkcích zmiňovaných ve větě.

To znamená: vzhledem k tomu, posloupnost nezávislých a stejně rozdělené náhodné proměnné , z nichž každá má průměr nula a pozitivní rozptyl , je-li navíc třetí absolutní moment je konečný, pak kumulativní distribuční funkce z standardizovaný vzorek střední hodnota a standardní normální distribuce se liší (ve svislém směru, v grafu) nejvýše o stanovenou částku. Všimněte si, že chybová aproximace pro všechna n (a tedy omezuje rychlost konvergence na neurčitou n dostatečně velký) je ohraničen pořadí z n ^-1/2 .

Vypočtené hodnoty konstanty C se v průběhu let výrazně snížily, z původní hodnoty 7,59 Esseen (1942) , na 0,7882 van Beek (1972) , poté 0,7655 Shiganov (1986) , poté 0,7056 Ševtsova (2007) , poté 0,7005 Ševtsové (2008) , poté 0,5894 Tyurina (2009) , poté 0,5129 Koroleva a Ševtsové (2010a) , poté 0,4785 Tyurina (2010) . Podrobný přehled lze najít v příspěvcích Korolev & Ševtsová (2010a) a Korolev & Ševtsova (2010b) . Nejlepší odhad z roku 2012, C  <0,4748, vyplývá z nerovnosti

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ vlevo | F_ {n} (x) - \ Phi (x) \ vpravo | \ leq {0,33554 (\ rho +0,415 \ sigma ^ {3} ) \ over \ sigma ^ {3} {\ sqrt {n}}},}$

kvůli Shevtsové (2011) , protože σ ³  ≤ ρ a 0,33554 · 1,415 <0,4748. Pokud však ρ ≥ 1,286σ ³ , pak odhad

${\ displaystyle \ sup _ {x \ v \ mathbb {R}} \ vlevo | F_ {n} (x) - \ Phi (x) \ vpravo | \ leq {0,3328 (\ rho +0,429 \ sigma ^ {3} ) \ over \ sigma ^ {3} {\ sqrt {n}}},}$

což dokazuje i Shevtsova (2011) , poskytuje ještě přísnější horní odhad.

Esseen (1956) dokázal, že konstanta uspokojuje i dolní mez

${\ displaystyle C \ geq {\ frac {{\ sqrt {10}} + 3} {6 {\ sqrt {2 \ pi}}}} \ přibližně 0,40973 \ přibližně {\ frac {1} {\ sqrt {2 \ pi}}} + 0,01079.}$

Neidenticky distribuované sčítání

Nechť X ₁ , X ₂ , ..., jsou nezávislé náhodné proměnné s E ( X _i ) = 0, E ( X _i ² ) = σ _i ² > 0 a E (| X _i | ³ ) = ρ _i < ∞. Také nechte

${\ displaystyle S_ {n} = {X_ {1} + X_ {2} + \ cdots + X_ {n} \ přes {\ sqrt {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2} + \ cdots + \ sigma _ {n} ^ {2}}}}}$

být normalizovaný n -tý dílčí součet. Označme F _n CDF z S _n a Φ CDF z normovaného normálního rozdělení . Kvůli pohodlí označte

${\ displaystyle {\ vec {\ sigma}} = (\ sigma _ {1}, \ ldots, \ sigma _ {n}), \ {\ vec {\ rho}} = (\ rho _ {1}, \ ldots, \ rho _ {n}).}$

V roce 1941 Andrew C. Berry dokázal, že pro všechna n existuje absolutní konstanta C ₁ taková

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ vlevo | F_ {n} (x) - \ Phi (x) \ vpravo | \ leq C_ {1} \ cdot \ psi _ {1}, \ \ \ \ (2)}$

kde

${\ displaystyle \ psi _ {1} = \ psi _ {1} {\ big (} {\ vec {\ sigma}}, {\ vec {\ rho}} {\ big)} = {\ Big (} { \ textstyle \ sum \ limity _ {i = 1} ^ {n} \ sigma _ {i} ^ {2}} {\ Big)} ^ {- 1/2} \ cdot \ max _ {1 \ leq i \ leq n} {\ frac {\ rho _ {i}} {\ sigma _ {i} ^ {2}}}.}$

Nezávisle v roce 1942 Carl-Gustav Esseen dokázal, že pro všechna n existuje absolutní konstanta C ₀ taková

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ vlevo | F_ {n} (x) - \ Phi (x) \ vpravo | \ leq C_ {0} \ cdot \ psi _ {0}, \ \ \ \ (3)}$

kde

${\ displaystyle \ psi _ {0} = \ psi _ {0} {\ big (} {\ vec {\ sigma}}, {\ vec {\ rho}} {\ big)} = {\ Big (} { \ textstyle \ sum \ limity _ {i = 1} ^ {n} \ sigma _ {i} ^ {2}} {\ Big)} ^ {- 3/2} \ cdot \ sum \ limity _ {i = 1 } ^ {n} \ rho _ {i}.}$

Je snadné zajistit, aby ψ ₀ ≤ψ ₁ . Kvůli této okolnosti se nerovnost (3) běžně nazývá nerovnost Berry – Esseen a veličina ψ ₀ se nazývá Lyapunovův zlomek třetího řádu. Navíc v případě, že sčítání X ₁ , ..., X _n mají identické rozdělení

${\ displaystyle \ psi _ {0} = \ psi _ {1} = {\ frac {\ rho _ {1}} {\ sigma _ {1} ^ {3} {\ sqrt {n}}}},}$

a tedy hranice stanovené nerovnostmi (1), (2) a (3) se shodují odděleně od konstanty.

Pokud jde o C ₀ , dolní mez stanovená Esseenem (1956) samozřejmě zůstává v platnosti:

${\ displaystyle C_ {0} \ geq {\ frac {{\ sqrt {10}} + 3} {6 {\ sqrt {2 \ pi}}}} = 0,4097 \ ldots.}$

Horní hranice pro C ₀ byla následně snížena z původního odhadu 7,59 kvůli Esseenovi (1942) na (pouze s ohledem na nedávné výsledky) 0,9051 kvůli Zolotarevovi (1967) , 0,7975 kvůli van Beekovi (1972) , 0,7915 kvůli Shiganovovi (1986) ) , 0,6379 a 0,5606 kvůli Tyurinu (2009) a Tyurinu (2010) . Od roku 2011 je nejlepší odhad 0,5600, který získala Shevtsova (2010) .

Multidimenzionální verze

Stejně jako u vícerozměrné centrální limitní věty existuje vícerozměrná verze věty Berry – Esseen.

Nechť jsou nezávislé náhodné vektory, z nichž každý má střední nulu. Napište a předpokládejte, že je invertibilní. Dovolit být -dimenzionální Gaussian se stejnou střední a kovarianční maticí jako . Pak pro všechny konvexních množin , ${\ displaystyle X_ {1}, \ tečky, X_ {n}}$${\ displaystyle \ mathbb {R} ^ {d}}$${\ displaystyle S = \ součet _ {i = 1} ^ {n} X_ {i}}$${\ displaystyle \ Sigma = \ operatorname {Cov} [S]}$${\ displaystyle Z \ sim \ operatorname {N} (0, \ Sigma)}$${\ displaystyle d}$${\ displaystyle S}$${\ displaystyle U \ subseteq \ mathbb {R} ^ {d}}$

${\ displaystyle {\ big |} \ Pr [S \ v U] - \ Pr [Z \ v U] \, {\ big |} \ leq Cd ^ {1/4} \ gamma}$ ,

kde je univerzální konstanta a (třetí síla normy L ² ). ${\ displaystyle C}$${\ displaystyle \ gamma = \ suma _ {i = 1} ^ {n} \ operatorname {E} {\ big [} \ | \ Sigma ^ {- 1/2} X_ {i} \ | _ {2} ^ {3} {\ velký]}}$

Závislost na se předpokládá jako optimální, ale nemusí být. ${\ displaystyle d ^ {1/4}}$

Viz také

• Černoffova nerovnost
• Série Edgeworth
• Seznam nerovností
• Seznam matematických vět
• Koncentrační nerovnost

Poznámky

Reference

externí odkazy

• Gut, Allan a Holst Lars. Carl-Gustav Esseen , vyvoláno 15. března 2004.
• „Nerovnost Berry – Esseen“ , Encyclopedia of Mathematics , EMS Press , 2001 [1994]