Mentální výpočet - Mental calculation

Psychická vypočítavost je již dlouho součástí matematické výchovy.

Mentální výpočet se skládá z aritmetických výpočtů využívajících pouze lidský mozek , bez pomoci jakýchkoli zásob (například tužky a papíru) nebo zařízení, jako je kalkulačka . Lidé používají mentální výpočet, když nejsou k dispozici výpočetní nástroje, když je rychlejší než jiné způsoby výpočtu (například konvenční metody vzdělávacích institucí), nebo dokonce v konkurenčním kontextu . Mentální výpočet často zahrnuje použití specifických technik navržených pro konkrétní typy problémů. Lidé s neobvykle vysokou schopností provádět mentální výpočty se nazývají mentální kalkulačky nebo bleskové kalkulačky .

Mnoho z těchto technik využívá nebo se spoléhá na desítkovou číselnou soustavu. Výběr metody radix obvykle určuje, kterou metodu nebo metody použít.

Metody a techniky

Vyhánění devítek

Po použití aritmetické operace na dva operandy a získání výsledku lze ke zvýšení důvěry ve správnost výsledku použít následující postup:

Sečtěte číslice prvního operandu; jakýchkoli 9 s (nebo sady číslic, které se přidávají k 9) lze počítat jako 0.
Pokud má výsledný součet dvě nebo více číslic, sečtěte tyto číslice jako v prvním kroku; tento krok opakujte, dokud nebude mít výsledný součet pouze jednu číslici.
Opakujte kroky jeden a dva s druhým operandem. Existují dvě jednociferná čísla, jedno zhuštěné z prvního operandu a druhé zhuštěné z druhého operandu. (Tato jednociferná čísla jsou také zbytky, u nichž by člověk skončil, kdyby se původní operandy vydělily 9; matematicky vzato jsou to původní operandy modulo 9.)
Na dva kondenzované operandy použijte původně zadanou operaci a poté na výsledek operace použijte postup sčítání číslic.
Sečtěte číslice výsledku, které byly původně získány pro původní výpočet.
Pokud se výsledek kroku 4 nerovná výsledku kroku 5, pak je původní odpověď špatná. Pokud se oba výsledky shodují, pak může být původní odpověď správná, i když není zaručeno, že bude.

Příklad

Řekněme, že výsledky výpočtu 6338 × 79 se rovnají 500702

Sečtěte číslice 6338: (6 + 3 = 9, takže to spočítejte jako 0) + 3 + 8 = 11
Opakujte podle potřeby: 1 + 1 = 2
Sečtěte číslice 79: 7 + (9 počítáno jako 0) = 7
Proveďte původní operaci na kondenzovaných operandech a číslice součtu: 2 × 7 = 14; 1 + 4 = 5
Sečtěte číslice 500702: 5 + 0 + 0 + (7 + 0 + 2 = 9, což se počítá jako 0) = 5
5 = 5, takže je velká šance, že předpověď, že 6338 × 79 se rovná 500702, je správná.

Stejný postup lze použít u více operací, přičemž pro každou operaci opakujte kroky 1 a 2.

Odhad

Při kontrole mentálního výpočtu je užitečné na to myslet z hlediska škálování. Například při práci s velkými čísly, řekněme 1 531 × 19 625, odhad instruuje člověka, aby si byl vědom počtu číslic očekávaných pro konečnou hodnotu. Užitečným způsobem kontroly je odhad. 1 531 je přibližně 1 500 a 19 625 je přibližně 20 000, takže výsledek přibližně 20 000 × 1 500 (30 000 000) by byl dobrým odhadem skutečné odpovědi (30 045 875). Pokud má tedy odpověď příliš mnoho číslic, došlo k chybě.

Faktory

Při násobení je užitečné mít na paměti, že faktory operandů stále zůstávají. Bylo by například nepřiměřené tvrdit, že 14 × 15 je 201. Protože 15 je násobek 5, měl by být také produkt. Podobně je 14 násobkem 2, takže by měl být produkt rovnoměrný. Kromě toho jakékoli číslo, které je násobkem obou 5 a 2, je nutně násobkem 10 a v desítkové soustavě by skončilo 0. Správná odpověď je 210. Je to násobek 10, 7 (další hlavní faktor ze 14) a 3 (druhý hlavní faktor 15).

Výpočet rozdílů: a - b

Přímý výpočet

Když jsou číslice b všechny menší než odpovídající číslice a , lze výpočet provádět číslice po číslici. Vyhodnoťte například 872 - 41 jednoduše odečtením 1 od 2 na místě jednotek a 4 od 7 na místě desítek: 831.

Nepřímý výpočet

Pokud výše uvedená situace neplatí, existuje další metoda známá jako nepřímý výpočet.

Výhledová metoda půjčky

Tuto metodu lze použít k odečtení čísel zleva doprava, a pokud vše, co je požadováno, je přečíst výsledek nahlas, vyžaduje to málo paměti uživatele, dokonce i k odečtení čísel libovolné velikosti.

Je zpracováno jedno místo najednou, zleva doprava.

Example:

          4075
        − 1844
        ------

Thousands: 4 − 1 = 3, look to right, 075 < 844, need to borrow.
           3 − 1 = 2, say "Two thousand".
           One is performing 3 - 1 rather than 4 - 1 because the column to the right is
           going to borrow from the thousands place.

Hundreds: 0 − 8 = negative numbers not allowed here.
          One is going to increase this place by using the number one borrowed from the
          column to the left. Therefore:
          10 − 8 = 2. It's 10 rather than 0, because one borrowed from the Thousands
          place. 75 > 44 so no need to borrow,
          say "two hundred"

Tens: 7 − 4 = 3, 5 > 4, so 5 - 4 = 1

Výsledkem je tedy 2231.

Výpočet produktů: a × b

Mnoho z těchto metod funguje kvůli distribuční vlastnosti .

Násobení libovolných dvou čísel připojením, odečtením a směrováním

Artem Cheprasov objevil metodu násobení, která umožňuje uživateli využít 3 kroky k rychlému vzájemnému znásobení čísel libovolné velikosti třemi jedinečnými způsoby.

Za prvé, metoda umožňuje uživateli během mezikroků k sobě přidávat čísla, na rozdíl od jejich sčítání nebo odčítání, aby se zrychlila rychlost násobení. Například místo sčítání nebo odčítání zprostředkovatelských výsledků, jako jsou 357 a 84, by uživatel mohl jednoduše spojit čísla dohromady (35784) za účelem zjednodušení a urychlení problému s násobením. Vzájemné spojování čísel pomáhá obejít zbytečné kroky, které se vyskytují v tradičních technikách násobení.

Za druhé, tato metoda podle potřeby používá záporná čísla, dokonce i při vynásobení dvou kladných celých čísel, aby se zrychlila rychlost násobení odečtením. To znamená, že dvě kladná celá čísla lze vynásobit dohromady, aby se získaly záporné mezikroky, a přesto je nakonec správná kladná odpověď. Tato záporná čísla jsou ve skutečnosti automaticky odvozena ze samotných kroků násobení, a jsou tedy jedinečná pro konkrétní problém. Opět jsou takové negativní mezikroky navrženy tak, aby pomohly urychlit mentální matematiku.

Konečně, dalším unikátním aspektem použití této metody je, že si uživatel může vybrat jednu z několika různých „cest násobení“ k danému konkrétnímu problému s násobením na základě svých subjektivních preferencí nebo silných a slabých stránek s konkrétními celými čísly.

Navzdory stejným počátečním celým číslům vydávají různé cesty násobení různá mezičísla, která jsou pro uživatele při odvozování automaticky odvozena. Někteří z těchto zprostředkovatelů mohou být jednodušší než ostatní (např. Někteří uživatelé mohou najít trasu, která používá zápornou hodnotu 7, zatímco jiná trasa používá 5 nebo 0, s nimiž je pro většinu lidí obvykle snazší mentálně pracovat, ale ne ve všech případech ).

Pokud se zdá, že jedna „trasa“ je pro jednoho žáka těžší než jiná trasa a její mezilehlá čísla, může si tento student jednoduše zvolit jinou jednodušší cestu násobení, přestože jde o stejný původní problém.

Formule „Konce pěti“

V případě jakéhokoli problému s násobením 2 číslic na 2 číslice, pokud obě čísla končí na pět, lze k jejich rychlému vynásobení použít následující algoritmus:

${\ displaystyle Ex: 35 \ times 75}$

Jako předběžný krok jednoduše zaokrouhlete menší číslo dolů a větší nahoru na nejbližší násobek deseti. V tomto případě:

${\ textstyle 35-5 = 30 = X}$

${\ Displaystyle 75+5 = 80 = Y}$

Algoritmus zní následovně:

${\ displaystyle (X \ times Y) +50 (t_ {1} -t_ {2})+25}$

Kde t ₁ je jednotka desítek původního většího čísla (75) a t ₂ je jednotka desítek původního menšího čísla (35).

${\ displaystyle = 30 \ times 80+50 (7-3)+25 = 2625}$

Autor také nastiňuje další podobný algoritmus, pokud chceme místo toho zaokrouhlit původní větší číslo dolů a původní menší číslo nahoru.

Formule „Dlužníka“

Pokud jsou dvě čísla v stejné vzdálenosti od nejbližšího násobku 100, lze k nalezení produktu použít jednoduchý algoritmus.

Jako jednoduchý příklad:

${\ displaystyle 33 \ times 67}$

Obě čísla jsou ve stejné vzdálenosti (33 pryč) od svého nejbližšího násobku 100 (0, respektive 100).

Jako předběžný krok jednoduše zaokrouhlete menší číslo dolů a větší nahoru na nejbližší násobek deseti. V tomto případě:

${\ textstyle 33-3 = 30 = X}$

${\ Displaystyle 67+3 = 70 = Y}$

Algoritmus zní následovně:

${\ displaystyle (X \ times Y)+u_ {1} \ times u_ {2}+u_ {2} (T_ {1} -T_ {2})}$

Kde u ₁ je číslice původního většího (67) jednotek a u ₂ je číslice původního menšího (33) jednotek. T ₁ je desítky číslic původního většího čísla a T ₂ jsou desítky číslic původního většího čísla vynásobené jejich příslušnou mocninou (v tomto případě 10, pro desítky číslic).

A tak:

${\ Displaystyle (30 \ times 70) +7 \ times 3+3 (60-30) = 2100+21+90 = 2211}$

Násobení libovolných 2místných čísel

Chcete-li snadno znásobit libovolná 2místná čísla dohromady, použijte jednoduchý algoritmus (kde a je desítka číslice prvního čísla, b je číslice prvního čísla, c je desítka druhého čísla a d je jedna číslice druhého čísla):

{\ Displaystyle (10a+b) \ cdot (10c+d)}

{\ Displaystyle = 100 (a \ cdot c) +10 (b \ cdot c) +10 (a \ cdot d)+b \ cdot d}

Například,

{\ Displaystyle 23 \ cdot 47 = 100 (2 \ cdot 4) +10 (3 \ cdot 4) +10 (2 \ cdot 7) +3 \ cdot 7}

  800
 +120
 +140
 + 21
-----
 1081

Všimněte si, že je to totéž jako konvenční součet dílčích produktů, jen s krátkostí přepracováno. Aby se minimalizoval počet prvků uchovávaných v paměti, může být vhodné nejprve provést součet multiplikačního produktu „kříž“ a poté přidat další dva prvky:

{\ Displaystyle (a \ cdot d+b \ cdot c) \ cdot 10}

{\ displaystyle {}+b \ cdot d}

[z nichž pouze desítky číslic budou zasahovat do prvního výrazu]

{\ displaystyle {}+a \ cdot c \ cdot 100}

tj. v tomto příkladu

(12 + 14) = 26, 26 × 10 = 260,

ke kterému je snadné přidat 21: 281 a poté 800: 1081

Snadná mnemotechnická pomůcka pro toto by byla FOIL . F znamená první, O znamená vnější, I znamená vnitřní a L znamená poslední. Například:

{\ Displaystyle 75 \ cdot 23}

a

{\ Displaystyle ab \ cdot cd}

kde 7 je a , 5 je b , 2 je c a 3 je d .

Zvážit

{\ Displaystyle a \ cdot c \ cdot 100+ (a \ cdot d+b \ cdot c) \ cdot 10+b \ cdot d}

tento výraz je analogický jakémukoli číslu v základně 10 se stovkami, desítkami a jednotkami. Na FOIL lze také pohlížet jako na číslo, kde F jsou stovky, OI desítky a L ty.

${\ Displaystyle a \ cdot c}$ je součin první číslice každého ze dvou čísel; F.

${\ Displaystyle (a \ cdot d+b \ cdot c)}$ je součet součinu vnějších a vnitřních číslic; OI.

${\ Displaystyle b \ cdot d}$ je součin poslední číslice každého ze dvou čísel; L.

Násobení 2 nebo jinými malými čísly

Pokud je jedno vynásobené číslo dostatečně malé na to, aby se snadno vynásobilo jakoukoli jedinou číslicí, lze produkt snadno vypočítat číslici po číslici zprava doleva. To je obzvláště snadné pro vynásobení 2, protože nosná číslice nemůže být větší než 1.

Například pro výpočet 2 × 167: 2 × 7 = 14, takže konečná číslice je 4 , přičemž 1 se nese a přičte se k 2 × 6 = 12, čímž se získá 13, takže další číslice je 3 s 1 nesenou a přičteno k 2 × 1 = 2, čímž se získá 3 . Produkt je tedy 334.

Násobení 5

Chcete -li číslo vynásobit 5,

1. Nejprve vynásobte toto číslo 10, poté jej vydělte 2. Tyto dva kroky jsou zaměnitelné, tj. Lze číslo snížit na polovinu a poté vynásobit.

Následující algoritmus je rychlý způsob, jak dosáhnout tohoto výsledku:

2. Přidejte nulu na pravou stranu požadovaného čísla. (A.) 3. Dále, počínaje číslicí úplně vlevo, vydělte 2 (B.) a připojte každý výsledek v příslušném pořadí k vytvoření nového čísla; (zlomkové odpovědi by měly být zaokrouhleny dolů na nejbližší celé číslo).

EXAMPLE: Multiply 176 by 5.
     A. Add a zero to 176 to make 1760.
     B. Divide by 2 starting at the left.
           1. Divide 1 by 2 to get .5, rounded down to zero.
           2. Divide 7 by 2 to get 3.5, rounded down to 3.
           3. Divide 6 by 2 to get 3. Zero divided by two is simply zero.

Výsledné číslo je 0330. (Toto není konečná odpověď, ale první aproximace, která bude upravena v následujícím kroku :)

     C. Add 5 to the number that follows any single numeral
        in this new number that was odd before dividing by two;

PŘÍKLAD: 176 (PRVNÍ, DRUHÉ TŘETÍ MÍSTA):

           1.The FIRST place is 1, which is odd. ADD 5 to the numeral after
             the first place in the new number (0330) which is 3; 3+5=8.
         
           2.The number in the second place of 176, 7, is also odd. The
             corresponding number (0 8 3 0) is increased by 5 as well;
             3+5=8.

           3.The numeral in the third place of 176, 6, is even, therefore
             the final number, zero, in the answer is not changed. That
             final answer is 0880.
             The leftmost zero can be omitted, leaving 880.
             So 176 times 5 equals 880.

PŘÍKLAD: Vynásobte 288 číslem 5.

A. Rozdělte 288 na 2. Každou číslici můžete rozdělit jednotlivě, abyste získali 144. (Rozdělení menšího čísla je snazší.)

B. Vynásobte 10. Přidejte nulu, abyste získali výsledek 1440.

Násobení 9

Protože 9 = 10 - 1, vynásobte číslo devíti, vynásobte jej 10 a poté od výsledku odečtěte původní číslo. Například 9 × 27 = 270 - 27 = 243.

Tuto metodu lze upravit tak, aby se vynásobila osmi místo devíti, a to zdvojnásobením odečítaného počtu; 8 × 27 = 270 - (2 × 27) = 270 - 54 = 216.

Podobně sčítáním namísto odčítání lze stejné metody použít k vynásobení čísly 11 a 12 (i když existují jednodušší metody pro vynásobení číslem 11).

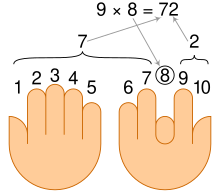
Pomocí rukou: 1–10 vynásobeno 9

Výpočet 9 × 8 pomocí prstů

Chcete -li použít tuto metodu, musíte položit ruce před sebe, dlaněmi směrem k nim. Přiřaďte levý palec 1, levý index 2 a tak dále až k pravému palci je deset. Každé "|" symbolizuje zdvižený prst a „ -“ představuje ohnutý prst.

1 2 3 4 5  6 7 8 9 10
| | | | |  | | | | |
left hand  right hand

Ohněte prst, který představuje číslo, které má být vynásobeno devíti.

Př .: 6 × 9 by bylo

| | | | |  − | | | |

Pravý malíček je dole. Vezměte počet prstů stále zvednutých vlevo od ohnutého prstu a připravte jej na počet prstů vpravo.

Příklad: Zbývá pět prstů pravého malíčku a čtyři napravo od pravého malíčku. Takže 6 × 9 = 54.

    5           4
| | | | |  − | | | |

Násobení 10 (a mocninami deseti)

Chcete -li vynásobit celé číslo 10, jednoduše přidejte na konec čísla 0 navíc. Chcete-li vynásobit celé číslo 10, přesuňte desetinnou čárku o jednu číslici doprava.

Pro desítku obecně platí, že pro vynásobení 10 ⁿ (kde n je celé číslo) přesuňte desetinnou čárku n číslic doprava. Pokud je n záporné, přesuňte desetinné | n | číslice vlevo.

Násobení 11

U jednociferných čísel jednoduše duplikujte číslo na desítky, například: 1 × 11 = 11, 2 × 11 = 22, až 9 × 11 = 99.

Součin pro jakékoli větší nenulové celé číslo lze najít pomocí řady přírůstků ke každé z jeho číslic zprava doleva, po dvou najednou.

Nejprve vezměte číslici a zkopírujte ji do dočasného výsledku. Dále, počínaje číslicí násobitele, přidejte každou číslici k číslici nalevo. Každý součet se pak přičte nalevo od výsledku před všechny ostatní. Pokud se číslo rovná 10 nebo vyšší, vezměte desítky, které budou vždy 1, a přeneste je do dalšího sčítání. Nakonec zkopírujte multiplikátor úplně vlevo (nejvyšší hodnota) na přední stranu výsledku, v případě potřeby přidejte přenesenou 1, abyste získali konečný produkt.

V případě záporné hodnoty 11, multiplikátor nebo obojí aplikujte na konečný produkt znaménko podle normálního násobení obou čísel.

Podrobný příklad 759 × 11:

Číslice jednotek multiplikátoru 9 je zkopírována do dočasného výsledku.
- výsledek: 9
Přidejte 5 + 9 = 14, takže 4 se umístí na levou stranu výsledku a ponese 1.
- výsledek: 49
Podobně sečte 7 + 5 = 12, poté přičtěte 1, abyste získali 13. Umístěte 3 na výsledek a vezměte 1.
- výsledek: 349
Přidejte přenesenou 1 k číslici s nejvyšší hodnotou v multiplikátoru, 7 + 1 = 8, a zkopírujte do výsledku.
- Konečný produkt 759 × 11: 8349

Další příklady:

−54 × −11 = 5 5+4 (9) 4 = 594
999 × 11 = 9+1 (10) 9+9+1 (9) 9+9 (8) 9 = 10989
- Všimněte si zpracování 9+1 jako nejvyšší hodnoty číslice.
−3478 × 11 = 3 3+4+1 (8) 4+7+1 (2) 7+8 (5) 8 = −38258
62473 × 11 = 6 6+2 (8) 2+4+1 (7) 4+7+1 (2) 7+3 (0) 3 = 687203

Další metodou je jednoduše vynásobit číslo 10 a přidat původní číslo k výsledku.

Například:

17 × 11

     17 × 10 = 170

170 + 17 = 187

17 × 11 = 187

Poslední snadný způsob:

Pokud má někdo dvouciferné číslo, vezměte ho a sečtěte obě čísla dohromady, vložte tento součet doprostřed a člověk může dostat odpověď.

Například: 24 x 11 = 264, protože 2 + 4 = 6 a 6 je umístěno mezi 2 a 4.

Druhý příklad: 87 x 11 = 957, protože 8 + 7 = 15, takže 5 jde mezi 8 a 7 a 1 je přeneseno do 8. Takže je to v zásadě 857 + 100 = 957.

Nebo pokud se 43 x 11 rovná první 4+3 = 7 (pro desítky), pak 4 je pro stovky a 3 je pro desítky. A odpověď je 473

Násobení dvou dvouciferných čísel mezi 11 a 19

Chcete -li snadno znásobit 2 číslice dohromady mezi 11 a 19, použijte jednoduchý algoritmus (kde a je číslice prvního čísla b a číslice druhého čísla druhého):

(10+a)×(10+b)
100 + 10×(a+b) + a×b

which can be visualized as three parts to be added:

1
xx
 yy

for example:

17×16

1               = 100
13    (7+6)     = 10×(a+b)
 42   (7×6)     = a×b
272   (total)

Pomocí rukou: 6–10 vynásobeno dalším číslem 6–10

Výpočet 9 × 8 a 7 × 6

Tato technika umožňuje znásobit číslo od 6 do 10 dalším číslem od 6 do 10.

Přiřaďte 6 malíčku, 7 prsteníku, 8 prostředníku, 9 ukazováčku a 10 palci. Dotkněte se společně dvou požadovaných čísel. Bod kontaktu a níže je považován za sekci „dole“ a vše nad dvěma prsty, které se dotýkají, je součástí sekce „nahoře“. Odpověď se vytvoří tak, že se desetinásobek celkového počtu „dolních“ prstů přičte k součinu počtu levých a pravých „horních“ prstů.

Například 9 × 6 by vypadalo takto, přičemž by se levý ukazováček dotýkal pravého malíčku:

                               =10==   :right thumb              (top)
                               ==9==   :right index finger       (top)
                               ==8==   :right middle finger      (top)
        left thumb:   =10==    ==7==   :right ring finger        (top)                    
 left index finger:   --9---><---6--   :right little finger      (BOTTOM)  
left middle finger:   --8--                                      (BOTTOM)
  left ring finger:   --7--                                      (BOTTOM)
left little finger:   --6--                                      (BOTTOM)

V tomto příkladu je 5 prstů „dole“ (levý rejstřík, prostředník, prsten a malé prsty plus pravý malíček), 1 levý „horní“ prst (levý palec) a 4 pravé „horní“ prsty (pravý palec, ukazováček, prostředník a prsteníček). Výpočet tedy probíhá následovně: 9 × 6 = (10 × 5) + (1 × 4) = 54.

Zvažte další příklad, 8 × 7:

                               =10==   :right thumb              (top)
        left thumb:   =10==    ==9==   :right index finger       (top)
 left index finger:   ==9==    ==8==   :right middle finger      (top)
left middle finger:   --8---><---7--   :right ring finger        (BOTTOM)
  left ring finger:   --7--    --6--   :right little finger      (BOTTOM)
left little finger:   --6--                                      (BOTTOM)

Pět dolních prstů tvoří 5 desítek nebo 50. Dva levé horní prsty a tři pravé horní prsty vytvářejí součin 6. Jejich součtem vznikne odpověď, 56.

Další příklad, tentokrát s použitím 6 × 8:

 --8---><---6--
 --7--
 --6--

Čtyři desítky (dole), plus dvakrát čtyři (nahoře) dává 40 + 2 × 4 = 48.

Zde je, jak to funguje: každý prst je číslo mezi 6 a 10. Když se člověk připojí prsty reprezentující x a y , bude 10 - x „top“ prsty a x - 5 „spodní“ prsty na levé straně; pravá ruka bude mít 10 - y „horních“ prstů a y - 5 „dolních“ prstů.

Nechat

{\ displaystyle \, t_ {L} = 10-x \,}

(počet „horních“ prstů na levé ruce)

{\ Displaystyle \, t_ {R} = 10-y \,}

(počet „horních“ prstů na pravé ruce)

{\ displaystyle \, b_ {L} = x-5 \,}

(počet prstů „dole“ na levé ruce)

{\ displaystyle \, b_ {R} = y-5 \,}

(počet prstů „dole“ na pravé ruce)

Poté se postupuje podle výše uvedených pokynů

{\ Displaystyle \, 10 (b_ {L}+b_ {R})+t_ {L} t_ {R}}

{\ Displaystyle \, = 10 [(x-5)+(y-5)]+(10-x) (10-y)}

{\ Displaystyle \, = 10 (x+y-10)+(100-10x-10y+xy)}

{\ Displaystyle \, = [10 (x+y) -100]+[100-10 (x+y)+xy]}

{\ Displaystyle \, = [10 (x+y) -10 (x+y)]+[100-100]+xy}

{\ displaystyle \, = xy}

který je požadovaný produkt.

Vynásobením dvou čísel blízko a pod 100

Tato technika umožňuje snadné násobení čísel blízkých a pod 100. (90–99) Proměnnými budou dvě čísla, která se vynásobí.

Součin dvou proměnných v rozmezí 90–99 bude mít za následek 4místné číslo. Prvním krokem je nalezení jednociferné a desítkové číslice.

Odečtěte obě proměnné od 100, což bude mít za následek 2 jednociferné číslo. Součinem dvou jednociferných čísel budou poslední dvě číslice konečného produktu.

Dále odečtěte jednu ze dvou proměnných od 100. Poté odečtěte rozdíl od druhé proměnné. Tímto rozdílem budou první dvě číslice konečného produktu a výsledné 4místné číslo bude konečným produktem.

Příklad:

          95
        x 97
        ----

Last two digits: 100-95=5 (subtract first number from 100)
                 100-97=3 (subtract second number from 100)
                 5*3=15   (multiply the two differences)
                 Final Product- yx15

First two digits: 100-95=5 (Subtract the first number of the equation from 100)
                  97-5=92  (Subtract that answer from the second number of the equation)
                  Now, the difference will be the first two digits
                  Final Product- 9215

Alternate for first two digits
                  5+3=8    (Add the two single digits derived when calculating "Last two digits" in previous step)
                  100-8=92 (Subtract that answer from 100)
                  Now, the difference will be the first two digits
                  Final Product- 9215

Použití čtvercových čísel

Součin malých čísel lze vypočítat pomocí čtverců celých čísel; například pro výpočet 13 × 17 lze poznamenat, že 15 je průměr těchto dvou faktorů, a uvažovat o tom jako (15 - 2) × (15 + 2), tj. 15 ² - 2 ² . Vědět, že 15 ² je 225 a 2 ² je 4, jednoduché odčítání ukazuje, že 225 - 4 = 221, což je požadovaný produkt.

Tato metoda vyžaduje znát zpaměti určitý počet čtverců:

1 ² = 1	6 ² = 36	11 ² = 121	16 ² = 256	21 ² = 441	26 ² = 676
2 ² = 4	7 ² = 49	12 ² = 144	17 ² = 289	22 ² = 484	27 ² = 729
3 ² = 9	8 ² = 64	13 ² = 169	18 ² = 324	23 ² = 529	28 ² = 784
4 ² = 16	9 ² = 81	14 ² = 196	19 ² = 361	24 ² = 576	29 ² = 841
5 ² = 25	10 ² = 100	15 ² = 225	20 ² = 400	25 ² = 625	30 ² = 900

Čtvercová čísla

Může být užitečné si uvědomit, že rozdíl mezi dvěma po sobě následujícími čtverci je součet jejich příslušných odmocnin. Pokud tedy někdo ví, že 12 × 12 = 144 a přeje si vědět 13 × 13, vypočítá 144 + 12 + 13 = 169.

Důvodem je ( x + 1) ² - x ² = x ² + 2 x + 1 - x ² = x + ( x + 1)

x ² = ( x - 1) ² + (2 x - 1)

Vyrovnávání libovolného čísla

Vezměte dané číslo a přidejte a odečtěte k němu určitou hodnotu, která vám usnadní násobení. Například:

492 ²

492 se blíží 500, což lze snadno vynásobit. Sečtením a odečtením 8 (rozdíl mezi 500 a 492) získáte

492 -> 484, 500

Vynásobením těchto čísel získáte 242 000 (To lze provést efektivně vydělením 484 2 = 242 a vynásobením 1000). Nakonec k výsledku přičtěte rozdíl (8) na druhou (8 ² = 64):

492 ² = 242 064

Důkaz následuje:

{\ Displaystyle n^{2} = n^{2}}

{\ Displaystyle n^{2} = (n^{2} -a^{2})+a^{2}}

{\ Displaystyle n^{2} = (n^{2} -an+an-a^{2})+a^{2}}

{\ Displaystyle n^{2} = (na) (n+a)+a^{2}}

Kvadratura libovolného 2místného celého čísla

Tato metoda vyžaduje zapamatování čtverců jednociferných čísel 1 až 9.

Čtvereček mn , mn jako dvouciferné celé číslo, lze vypočítat jako

10 × m ( mn + n ) + n ²

Což znamená, že čtverec Mn lze nalézt přidáním n k Mn , vynásobený m , přidáním 0 až do konce a nakonec bylo přidáno čtverec n .

Například 23 ² :

23 ²

= 10 × 2 (23 + 3) + 3 ²

= 10 × 2 (26) + 9

= 520 + 9

= 529

Takže 23 ² = 529.

Srovnáním čísla končícího na 5

Vezměte číslice, které předcházejí pěti: abc5 , kde a, b, a c jsou číslice
Vynásobte toto číslo samostatně plus jedno: abc ( abc + 1)
Vezměte výše uvedený výsledek a připojte 25 na konec
- Příklad: 85 × 85
  1. 8
  2. 8 × 9 = 72
  3. Takže 85 ² = 7225
- Příklad: 125 ²
  1. 12
  2. 12 × 13 = 156
  3. Takže 125 ² = 15 625
- Matematické vysvětlení

(10 x + 5) ²	= (10 x + 5) (10 x + 5)
	= 100 x ² + 100 x + 25
	= 100 ( x ² + x ) + 25
	= 100 x ( x + 1) + 25

Čtvercová čísla velmi blízko 50

Předpokládejme, že je třeba umocnit číslo n blízko 50.

Číslo může být vyjádřeno jako n = 50 - a, takže jeho čtverec je (50− a ) ² = 50 ² - 100 a + a ² . Ví, že 50 ² je 2500. Takže jedna odečítá 100 od 2500, a pak přidat na ² .

Příklad: Řekněme, že chceme čtverci 48, což je 50 - 2. Odečteme 200 od 2500 a přičteme 4 a dostaneme n ² = 2304. U čísel větších než 50 ( n = 50 + a ) přidejte 100 × a místo odečíst to.

Obdélník celého čísla od 26 do 74

Tato metoda vyžaduje zapamatování čtverců od 1 do 24.

Čtverec n (nejsnadněji se vypočítá, když n je mezi 26 a 74 včetně) je

(50 - n ) ² + 100 ( n - 25)

Jinými slovy, druhá mocnina čísla je druhá mocnina jeho rozdílu od padesáti přičtených k stonásobku rozdílu čísla a dvaceti pěti. Například na čtverec 62:

(−12) ² + [(62-25) × 100]

= 144 + 3 700

= 3,844

Vyrovnávání celých čísel blízko 100 (např. Od 76 do 124)

Tato metoda vyžaduje zapamatování čtverců od 1 do a, kde a je absolutní rozdíl mezi n a 100. Například studenti, kteří si zapamatovali své čtverce od 1 do 24, mohou tuto metodu použít na jakékoli celé číslo od 76 do 124.

Čtverec n (tj. 100 ± a ) je

100 (100 ± 2 a ) + a ²

Jinými slovy, druhá mocnina čísla je druhá mocnina jeho rozdílu od 100 přičtená k součinu sta a rozdílu sta a součinu dvou a rozdílu sta a čísla. Například na čtverec 93:

100 (100 - 2 (7)) + 7 ²

= 100 × 86 + 49

= 8 600 + 49

= 8 649

Další způsob, jak se na to podívat, by byl tento:

93 ² =? (je −7 ze 100)

93 - 7 = 86 (toto dává první dvě číslice)

(−7) ² = 49 (toto jsou druhé dvě číslice)

93 ² = 8649

Další příklad:

 82² = ?      (is −18 from 100)
 82 − 18 = 64   (subtract.  First digits.)
 (−18)² = 324 (second pair of digits. One will need to carry the 3.)
 82² = 6724

Kvadratura libovolného celého čísla blízkého 10 ⁿ (např. 976 až 1024, 9976 až 10024 atd.)

Tato metoda je přímým rozšířením výše uvedeného vysvětlení pro kvadraturu celého čísla blízko 100.

 1012² = ?         (1012 is +12 from 1000)
 (+12)² = 144      (n trailing digits)
 1012 + 12 = 1024  (leading digits)
 1012² = 1024144

 9997² = ?          (9997 is -3 from 10000)
 (-3)² = 0009       (n trailing digits)
 9997 - 3 = 9994    (leading digits)
 9997² = 99940009

Kvadratura libovolného celého čísla blízko m × 10 ⁿ (např. 276 až 324, 4976 až 5024, 79976 až 80024)

Tato metoda je přímým rozšířením výše uvedeného vysvětlení pro celá čísla blízká 10 ⁿ .

 407² = ?        (407 is +7 from 400)
 (+7)² = 49      (n trailing digits)
 407 + 7 = 414
 414 × 4 = 1656  (leading digits; note this multiplication by m wasn't needed for integers from 76 to 124 because their m = 1)
 407² = 165649

 79991² = ?          (79991 is -9 from 80000)
 (-9)² = 0081        (n trailing digits)
 79991 - 9
 79982 × 8 = 639856  (leading digits)
 79991² = 6398560081

Hledání kořenů

Přibližné odmocniny

Jednoduchý způsob, jak aproximovat druhou odmocninu čísla, je použít následující rovnici:

{\ Displaystyle {\ text {root}} \ simeq {\ text {známý odmocnina}}-{\ frac {{\ text {známý čtverec}}-{\ text {neznámý čtverec}}} {2 \ krát {\ text {známá odmocnina}}}} \,}

Čím blíže je známý čtverec k neznámému, tím přesnější je aproximace. Například pro odhad odmocniny na 15 bychom mohli začít s vědomím, že nejbližší dokonalý čtverec je 16 (4 ² ).

{\ Displaystyle {\ begin {aligned} {\ text {root}} & \ simeq 4-{\ frac {16-15} {2 \ times 4}} \\ & \ simeq 4-0,125 \\ & \ simeq 3,875 \\\ end {aligned}} \, \!}

Odhadovaná odmocnina z 15 je tedy 3,875. Skutečná odmocnina z 15 je 3,872983 ... Jedna věc, kterou je třeba poznamenat, je, že bez ohledu na původní odhad byl odhadovaná odpověď vždy větší než skutečná odpověď kvůli nerovnosti aritmetických a geometrických průměrů . Člověk by se tedy měl pokusit zaokrouhlit odhadovanou odpověď dolů.

Všimněte si, že pokud n ² je nejbližší dokonalý čtverec k požadovanému čtverci x a d = x - n ² je jejich rozdíl, je vhodnější vyjádřit tuto aproximaci ve formě smíšené frakce jako . V předchozím příkladu je tedy druhá odmocnina z 15 Jako další příklad je druhá odmocnina ze 41, zatímco skutečná hodnota je 6,4031 ... ${\ displaystyle n {\ tfrac {d} {2n}}}$ ${\ displaystyle 4 {\ tfrac {-1} {8}}.}$ ${\ displaystyle 6 {\ tfrac {5} {12}} = 6,416}$

Derivace

Podle definice, pokud r je druhá odmocnina x, pak

{\ Displaystyle \ mathrm {r} ^{2} = x \, \!}

Jeden pak předefinuje kořen

{\ Displaystyle \ mathrm {r} = ab \, \!}

kde a je známý kořen (4 z výše uvedeného příkladu) a b je rozdíl mezi známým kořenem a odpovědí, kterou hledáme.

{\ Displaystyle (ab)^{2} = x \, \!}

Rozšíření výnosů

{\ Displaystyle a^{2} -2ab+b^{2} = x \, \!}

Pokud je 'a' blízko cíle, bude 'b' dostatečně malé číslo, aby byl prvek rovnice zanedbatelný. Lze tedy vypadnout a změnit uspořádání rovnice na ${\ displaystyle {}+b^{2} \,}$ ${\ displaystyle {}+b^{2} \,}$

{\ Displaystyle b \ simeq {\ frac {a^{2} -x} {2a}} \, \!}

a proto

{\ Displaystyle \ mathrm {root} \ simeq a-{\ frac {a^{2} -x} {2a}} \, \!}

to lze snížit na

{\ Displaystyle \ mathrm {root} \ simeq {\ frac {a^{2}+x} {2a}} \, \!}

Extrahování kořenů dokonalých sil

Extrakce kořenů dokonalých sil se často praktikuje. Obtížnost úkolu nezávisí na počtu číslic dokonalé síly, ale na přesnosti, tj. Počtu číslic kořene. Kromě toho také závisí na pořadí kořene; nalezení dokonalých kořenů, kde je pořadí kořene coprime s 10, je poněkud snazší, protože číslice jsou míchány konzistentními způsoby, jako v další části.

Extrahování kořenů kostek

Snadný úkol pro začátečníka je extrahovat kořeny krychle z kostek dvouciferných čísel. Pokud například uvedeme 74088, určete, jaké dvouciferné číslo, když se jednou vynásobí a poté znovu vynásobí číslem, získá 74088. Ten, kdo zná metodu, rychle pozná odpověď 42, protože 42 ³ = 74088.

Než se naučíte postup, je nutné, aby si umělec zapamatoval kostky čísel 1-10:

1 ³ = 1	2 ³ = 8	3 ³ = 27	4 ³ = 64	5 ³ = 125
6 ³ = 216	7 ³ = 343	8 ³ = 512	9 ³ = 729	10 ³ = 1000

Všimněte si, že na číslici úplně vpravo je vzorec: sčítání a odčítání s 1 nebo 3. Počínaje od nuly:

0 ³ = 0
1 ³ = 1 nahoru 1
2 ³ = 8 dolů 3
3 ³ = 2 7 dolů 1
4 ³ = 6 4 dolů 3
5 ³ = 12 5 nahoru 1
6 ³ = 21 6 nahoru 1
7 ³ = 34 3 dolů 3
8 ³ = 51 2 dolů 1
9 ³ = 72 9 dolů 3
10 ³ = 100 0 nahoru 1

Extrahování odmocniny z krychle dvouciferného čísla jsou dva kroky. Například extrahování odmocniny 29791. Určete něčí místo (jednotky) dvouciferného čísla. Protože kostka končí na 1, jak je vidět výše, musí být 1.

Pokud dokonalá krychle končí na 0, musí její kořen na krychli končit na 0.
Pokud dokonalá kostka končí na 1, musí její kořen na konci 1.
Pokud dokonalá kostka končí na 2, její kořen na kostce musí končit na 8.
Pokud dokonalá kostka končí na 3, její kořen na kostce musí končit na 7.
Pokud dokonalá kostka končí na 4, musí její kořen na kostce končit na 4.
Pokud dokonalá kostka končí na 5, musí její kořen na kostce končit na 5.
Pokud dokonalá kostka končí na 6, musí její kořen na konci 6.
Pokud dokonalá krychle končí na 7, musí její kořen na 3.
Pokud dokonalá kostka končí na 8, její kořen na kostce musí končit na 2.
Pokud dokonalá kostka končí na 9, musí její kořen na kostce končit na 9.

Všimněte si, že každá číslice odpovídá sobě kromě 2, 3, 7 a 8, které jsou odečteny od deseti, aby se získala odpovídající číslice.

Druhým krokem je určit první číslici kořene dvouciferné krychle pohledem na velikost dané krychle. Chcete-li to provést, odeberte poslední tři číslice dané krychle (29791 → 29) a najděte největší krychli, která je větší než (zde je potřeba znát kostky čísel 1-10). Zde je 29 větší než 1 kostka, větší než 2 kostky, větší než 3 kostky, ale ne větší než 4 kostky. Největší krychle je větší než 3, takže první číslice dvouciferné krychle musí být 3.

Kořenová kostka 29791 je tedy 31.

Další příklad:

Najděte kořen krychle z 456533.
Kořen kostky končí v 7.
Po odebrání posledních tří číslic zůstává 456.
456 je větší než všechny kostky až 7 kostek.
První číslice kořene kostky je 7.
Kořenová kostka 456533 je 77.

Tento proces lze rozšířit na nalezení kořenů krychle, které jsou dlouhé 3 číslice, pomocí aritmetického modulo 11.

Tyto typy triků lze použít v jakémkoli kořenovém adresáři, kde je pořadí kořene coprime s 10; proto nefunguje v odmocnině, protože mocnina 2 se dělí na 10. 3 nerozděluje 10, takže fungují odmocniny.

Přibližný běžný logaritmus (log log 10)

K aproximaci běžného logaritmu (s přesností alespoň na jednu desetinnou čárku) je zapotřebí několik pravidel logaritmu a zapamatování několika logaritmů. Jeden musí vědět:

log (a × b) = log (a) + log (b)
log (a / b) = log (a) - log (b)
log (0) neexistuje
log (1) = 0
log (2) ~ .30
log (3) ~ 0,48
log (7) ~ 0,85

Z těchto informací lze najít logaritmus libovolného čísla 1-9.

log (1) = 0
log (2) ~ .30
log (3) ~ 0,48
log (4) = log (2 × 2) = log (2) + log (2) ~ .60
log (5) = log (10 /2) = log (10) - log (2) ~ .70
log (6) = log (2 × 3) = log (2) + log (3) ~ .78
log (7) ~ 0,85
log (8) = log (2 × 2 × 2) = log (2) + log (2) + log (2) ~ 0,90
log (9) = log (3 × 3) = log (3) + log (3) ~ 0,96
log (10) = 1 + log (1) = 1

Prvním krokem při sbližování běžného logaritmu je uvedení čísla uvedeného ve vědecké notaci. Například číslo 45 ve vědecké notaci je 4,5 × 10 ¹ , ale člověk tomu bude říkat a × 10 ^b . Dále najděte logaritmus a, který je mezi 1 a 10. Začněte tím, že najdete logaritmus 4, což je 0,60, a pak logaritmus 5, což je 0,70, protože 4,5 je mezi těmito dvěma. Dále, a dovednost v této oblasti přichází s praxí, umístěte 5 na logaritmickou stupnici mezi 0,6 a 0,7, někde kolem 0,653 (POZNÁMKA: skutečná hodnota dalších míst bude vždy větší, než kdyby byla umístěna na pravidelném měřítko. tj. dalo by se očekávat, že půjde na .650, protože je v polovině, ale místo toho bude o něco větší, v tomto případě .653) Jakmile získáte logaritmus a, jednoduše k němu přidejte b, abyste získali aproximace společného logaritmu. V tomto případě a + b = 0,653 + 1 = 1,653. Skutečná hodnota logu (45) ~ 1,65321.

Stejný postup platí pro čísla mezi 0 a 1. Například 0,045 by bylo zapsáno jako 4,5 × 10 ⁻² . Jediným rozdílem je, že b je nyní záporné, takže při sčítání jedničky se opravdu odečítá. Výsledkem by byl výsledek 0,653 - 2 nebo -1,347.

Mentální aritmetika jako psychologická dovednost

Fyzická námaha na správné úrovni může vést ke zvýšení výkonu mentálního úkolu , jako je provádění mentálních výpočtů, prováděných později. Bylo prokázáno, že během vysoké úrovně fyzické aktivity má negativní vliv na výkon duševních úkolů. To znamená, že příliš mnoho fyzické práce může snížit přesnost a výkon výpočtů mentální matematiky. Fyziologická opatření, konkrétně EEG , byla prokázána jako užitečná při indikaci duševní zátěže . Použití EEG jako měřítka duševní zátěže po různých úrovních fyzické aktivity může pomoci určit úroveň fyzické námahy, která bude pro duševní výkonnost nejpřínosnější. Předchozí práce, kterou na Michiganské technologické univerzitě provedla Ranjana Mehta, zahrnuje nedávnou studii, která zahrnovala účastníky zapojující se do souběžných duševních a fyzických úkolů. Tato studie zkoumala účinky mentálních požadavků na fyzickou výkonnost na různých úrovních fyzické námahy a nakonec zjistila pokles tělesné výkonnosti, když byly souběžně dokončovány duševní úkoly, s výraznějším účinkem na vyšší úrovni fyzické zátěže. Procedura Brown-Peterson je široce známý úkol využívající mentální aritmetiku. Tento postup, většinou používaný v kognitivních experimentech, naznačuje, že mentální odčítání je užitečné při testování účinků, které může mít udržovací zkouška na to, jak dlouho krátkodobá paměť trvá.

Mistrovství světa v mentálních výpočtech

První mistrovství světa v mentálních výpočtech se konalo v roce 1997. Tato událost se opakuje každý rok. Skládá se z řady různých úkolů, jako je sčítání deseti desetimístných čísel, násobení dvou osmimístných čísel, výpočet odmocnin, výpočet pracovních dnů pro daná data, výpočet odmocnin a některé překvapivé různé úkoly.

Světový pohár v mentální kalkulaci

První mistrovství světa v mentální kalkulaci (Mistrovství světa v mentální kalkulaci ) se konalo v roce 2004. Opakují se každý druhý rok. Skládá se ze šesti různých úkolů: sčítání deseti desetimístných čísel, násobení dvou osmimístných čísel, výpočet odmocnin a výpočet všedních dnů pro daná data, výpočet odmocnin plus nějaké překvapivé různé úkoly.

Memoriad - světová paměť, mentální výpočet a olympiáda v rychlém čtení

Memoriad je první platformou kombinující soutěže „mentální výpočet“, „paměť“ a „fotografické čtení“. Hry a soutěže se konají v roce olympijských her, každé čtyři roky. První Memoriad se konalo v Istanbulu , Turecku , v roce 2008. Druhá Memoriad konal v Antalya , Turkey dne 24-25 listopadu 2012. účastnil 89 závodníků z 20 zemí. Ceny a finanční odměny byly rozdány celkem pro 10 kategorií; z nichž 5 kategorií mělo co do činění s mentálním výpočtem (mentální sčítání, mentální násobení, mentální odmocniny (ne celé číslo), výpočet dat mentálního kalendáře a Flash Anzan).

Viz také

Reference

externí odkazy

Světový pohár v mentální kalkulaci
Memoriad - Světová mentální olympiáda
Tzourio-Mazoyer, Nathalie; Pesenti, Mauro; Zago, Laure; Crivello, Fabrice; Mellet, Emmanuel; Samson, Dana; Duroux, Bruno; Seron, Xavier; Mazoyer, Bernard (2001). „Mentální výpočet v zázračném stavu je udržován pravými prefrontálními a mediálními časovými oblastmi“. Přírodní neurověda . 4 (1): 103–7. doi : 10,1038/82831 . PMID 11135652 . S2CID 23829063 .
Rivera, SM; Reiss, AL; Eckert, MA; Menon, V (2005). „Vývojové změny v mentální aritmetice: Důkazy pro zvýšenou funkční specializaci v levé nižší parietální kůře“ . Mozková kůra . 15 (11): 1779–90. doi : 10,1093/cercor/bhi055 . PMID 15716474 .

Languages

In other projects

Mentální výpočet - Mental calculation

Metody a techniky

Vyhánění devítek

Odhad

Faktory

Výpočet rozdílů: a - b

Přímý výpočet

Nepřímý výpočet

Výhledová metoda půjčky

Výpočet produktů: a × b

Násobení libovolných dvou čísel připojením, odečtením a směrováním

Formule „Konce pěti“

Formule „Dlužníka“

Násobení libovolných 2místných čísel

Násobení 2 nebo jinými malými čísly

Násobení 5

Násobení 9

Pomocí rukou: 1–10 vynásobeno 9

Násobení 10 (a mocninami deseti)

Násobení 11

Násobení dvou dvouciferných čísel mezi 11 a 19

Pomocí rukou: 6–10 vynásobeno dalším číslem 6–10

Vynásobením dvou čísel blízko a pod 100

Použití čtvercových čísel

Čtvercová čísla

Vyrovnávání libovolného čísla

Kvadratura libovolného 2místného celého čísla

Srovnáním čísla končícího na 5

Čtvercová čísla velmi blízko 50

Obdélník celého čísla od 26 do 74

Vyrovnávání celých čísel blízko 100 (např. Od 76 do 124)

Kvadratura libovolného celého čísla blízkého 10 n (např. 976 až 1024, 9976 až 10024 atd.)

Kvadratura libovolného celého čísla blízko m × 10 n (např. 276 až 324, 4976 až 5024, 79976 až 80024)

Hledání kořenů

Přibližné odmocniny

Derivace

Extrahování kořenů dokonalých sil

Extrahování kořenů kostek

Přibližný běžný logaritmus (log log 10)

Mentální aritmetika jako psychologická dovednost

Mistrovství světa v mentálních výpočtech

Světový pohár v mentální kalkulaci

Memoriad - světová paměť, mentální výpočet a olympiáda v rychlém čtení

Viz také

Reference

externí odkazy

Kvadratura libovolného celého čísla blízkého 10 ⁿ (např. 976 až 1024, 9976 až 10024 atd.)

Kvadratura libovolného celého čísla blízko m × 10 ⁿ (např. 276 až 324, 4976 až 5024, 79976 až 80024)