Problém Monty Hall - Monty Hall problem
Problém Monty Hall je hlavolam, ve formě pravděpodobnostní hádanky, volně založený na americkém televizním herním pořadu Let's Make a Deal a pojmenovaný po původním hostiteli Monty Hall . Problém byl původně položená (i vyřešeny) v dopisu Steve Selvin na americký statistik v roce 1975. To se proslavil jako otázku čtenář Craiga F. Whitakera dopisu citoval Marilyn vos Savant sloupci je‘Zeptejte Marilyn" v Parade časopisu v roce 1990:
Předpokládejme, že jste v herní show a máte na výběr ze tří dveří: Za jedněmi dveřmi je auto; za ostatními, kozy. Vyberete dveře, řeknete č. 1, a hostitel, který ví, co je za dveřmi, otevře další dveře, řekněme č. 3, které mají kozu. Potom vám řekne: „Chcete si vybrat dveře č. 2?“ Je vaší výhodou změnit výběr?
Vos Savant odpověděl, že soutěžící by měl přejít k druhým dveřím. Podle standardních předpokladů má strategie přepínání a2/3 pravděpodobnost výhry auta, zatímco strategie, která zůstává u původní volby, má pouze a1/3 pravděpodobnost.
Když si hráč poprvé vybere, objeví se a 2/3šance, že auto stojí za některými dveřmi, které nebyly vybrány. Tato pravděpodobnost se nezmění poté, co hostitel otevře jedny z nevybraných dveří. Když hostitel poskytne informace o 2 nevybraných dveřích (odhalí, že jeden z nich za sebou nemá auto),2/3 šance, že auto bude za některými nevybranými dveřmi, spočívá na nevyvolaných a neodhalených dveřích, na rozdíl od 1/3 šanci, že auto bude za dveřmi, si soutěžící původně vybral.
Dané pravděpodobnosti závisí na konkrétních předpokladech, jak si hostitel a soutěžící vyberou své dveře. Klíčovým poznatkem je, že za těchto standardních podmínek existuje více informací o dveřích 2 a 3, než jaké byly k dispozici na začátku hry, když si dveře 1 vybral hráč: záměrná akce hostitele přidává hodnotu dveřím, které neměl rozhodnout se eliminovat, ale ne ten, který původně zvolil soutěžící. Dalším poznatkem je, že přepínání dveří je odlišná akce od náhodného výběru mezi dvěma zbývajícími dveřmi, protože první akce používá předchozí informace a druhá nikoli. Jiné možné chování hostitele, než je popsané, může odhalit jiné doplňkové informace nebo vůbec žádné a poskytnout různé pravděpodobnosti.
Mnoho čtenářů sloupku vos Savant odmítlo uvěřit, že přepnutí je prospěšné, a odmítli její vysvětlení. Poté, co se problém objevil v Parade , napsalo do časopisu přibližně 10 000 čtenářů, včetně téměř 1 000 s doktoráty , většina z nich označila vos Savant za špatnou. I když dostali vysvětlení, simulace a formální matematické důkazy, mnoho lidí stále nepřijalo, že přepínání je nejlepší strategie. Paul Erdős , jeden z nejplodnějších matematiků v historii, zůstal nepřesvědčivý, dokud mu nebyla ukázána počítačová simulace demonstrující předpokládaný výsledek vos Savanta.
Problém je paradoxem veridického typu, protože řešení Vos Savant je tak neintuitivní, že se může zdát absurdní, ale přesto je prokazatelně pravdivé. Problém Montyho Halla matematicky úzce souvisí s dřívějším problémem Tří vězňů a s mnohem starším paradoxem Bertrandovy skříňky .
Paradox
Steve Selvin napsal v roce 1975 dopis americkému statistikovi s popisem problému založeného na herní show Let's Make a Deal , v následujícím dopise jej nazval „problém Monty Hall“. Problém je matematicky ekvivalentní problému Tří vězňů popsaného ve sloupku Martina Gardnera „Matematické hry“ ve Scientific American v roce 1959 a Problém tří mušlí popsaný v Gardnerově knize Aha Gotcha .
Standardní předpoklady
Podle standardních předpokladů je pravděpodobnost výhry auta po přepnutí 2/3. Klíčem k tomuto řešení je chování hostitele. Nejasnosti ve verzi Parade explicitně nedefinují protokol hostitele. Řešení Marilyn vos Savant vytištěné vedle Whitakerovy otázky však implikuje a Selven i vos Savant výslovně definují roli hostitele takto:
- Hostitel musí vždy otevřít dveře, které soutěžící nevybral.
- Hostitel musí vždy otevřít dveře, aby odhalil kozu, nikdy ne auto.
- Hostitel musí vždy nabídnout možnost přepnout mezi původně zvolenými dveřmi a zbývajícími zavřenými dveřmi.
Pokud se některý z těchto předpokladů mění, může to změnit pravděpodobnost výhry přepnutím dveří, jak je podrobně popsáno v níže uvedené části . Typicky se také předpokládá, že auto je zpočátku skryto náhodně za dveřmi a že pokud si hráč zpočátku vybere auto, pak je výběr hostitele, které dveře ke skrývání kozy otevřou, náhodný. Někteří autoři, nezávisle nebo inkluzivně, předpokládají, že počáteční volba hráče je také náhodná.
Jednoduchá řešení
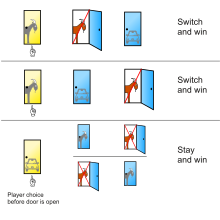
Řešení předložené vos Savantem v Parade ukazuje tři možná uspořádání jednoho auta a dvou koz za třemi dveřmi a výsledek setrvání nebo přepnutí po počátečním výběru dveří 1 v každém případě:
Za dveřmi 1 Za dveřmi 2 Za dveřmi 3 Výsledek, pokud zůstanete u dveří č. 1 Výsledek, pokud je nabídnuto přepnutí na dveře Koza Koza Auto Vyhrává koza Vyhrává auto Koza Auto Koza Vyhrává koza Vyhrává auto Auto Koza Koza Vyhrává auto Vyhrává koza
Hráč, který zůstane u původní volby, vyhrává pouze v jedné ze tří z těchto stejně pravděpodobných možností, zatímco hráč, který přepne, vyhrává ve dvou ze tří.
Intuitivní vysvětlení je to, že v případě, že soutěžící nejprve vybere kozu (2 ze 3 dveře), soutěžící bude vyhrát auto přepnutím protože ostatní kozy již nemůže být sebrán, zatímco v případě, že soutěžící nejprve zvedne automobil (1 ze 3 dveře), soutěžící nebude vyhrát auto přepnutím. Skutečnost, že hostitel následně odhalí kozu v jednom z nevybraných dveří, nic nemění na počáteční pravděpodobnosti.
Většina lidí došla k závěru, že na přepínání nezáleží, protože existují dvě neotevřené dveře a jedno auto a že je to volba 50/50. To by platilo, kdyby hostitel náhodně otevřel dveře, ale není tomu tak; otevřené dveře závisí na počátečním výběru hráče, takže předpoklad nezávislosti neobstojí. Než hostitel otevře dveře, objeví se a1/3pravděpodobnost, že auto stojí za každým vchodem. Pokud je vůz za dveřmi 1, hostitel může otevřít buď dveře 2, nebo dveře 3, takže pravděpodobnost, že auto bude za dveřmi 1 a hostitel otevře dveře 3, je1/3 × 1/2 = 1/6. Pokud je auto za dveřmi 2 (a hráč vybral dveře 1), hostitel musí otevřít dveře 3, takže pravděpodobnost, že auto bude za dveřmi 2 a hostitel otevře dveře 3, je1/3 × 1 = 1/3. Toto jsou jediné případy, kdy hostitel otevře dveře 3, takže pokud si hráč vybral dveře 1 a hostitel otevře dveře 3, auto je dvakrát častěji za dveřmi 2 než dveře 1. Klíčem je, že pokud je vůz za dveřmi 2 musí hostitel otevřít dveře 3, ale pokud je auto za dveřmi 1, hostitel může otevřít kterékoli dveře.
Dalším způsobem, jak porozumět řešení, je zvážit obě původní nevybrané dveře společně. Jak říká Cecil Adams : „Monty ve skutečnosti říká: můžete si nechat jedny dveře, nebo můžete mít druhé dveře.“ The2/3šance na nalezení vozu nebyla změněna otevřením jedněch z těchto dveří, protože Monty, který zná polohu auta, určitě odhalí kozu. Volba hráče poté, co hostitel otevře dveře, se neliší od toho, kdyby hostitel nabídl hráči možnost přepnout z původních vybraných dveří na sadu obou zbývajících dveří. Přepínač v tomto případě jasně dává hráči a2/3 pravděpodobnost výběru auta.
Jak říká Keith Devlin : „Když Monty otevřel dveře, říká soutěžícímu: Jsou dvě dveře, které jste si nevybrali, a pravděpodobnost, že cena bude za jedněmi z nich, je2/3. Pomůžu vám tím, že využiji své znalosti o tom, kde je cena, k otevření jedněch z těchto dvou dveří, abych vám ukázal, že cenu neskrývá. Nyní můžete využít těchto dodatečných informací. Vaše volba dveří A má šanci, že 1 ze 3 bude vítězem. To jsem nezměnil. Ale odstraněním dveří C jsem vám ukázal, že pravděpodobnost, že dveře B skryjí cenu, je 2 ku 3. “ “
Vos Savant navrhuje, že řešení bude intuitivnější s 1 000 000 dveřmi místo 3. V tomto případě je za nimi 999 999 dveří s kozami a jedny dveře s cenou. Poté, co hráč vybere dveře, hostitel otevře 999 998 zbývajících dveří. V průměru v 999 999 krát z 1 000 000 budou zbývající dveře obsahovat cenu. Intuitivně by se měl hráč zeptat, jak je pravděpodobné, že vzhledem k milionu dveří se jim podařilo zpočátku vybrat ten správný. Stibel a kol. Navrhli, aby se poptávka po pracovní paměti zdanila během problému Monty Hall a aby to lidi nutilo „sbalit“ své volby do dvou stejně pravděpodobných možností. Hlásí, že když se počet možností zvýší na více než 7 možností (7 dveří), lidé mají tendenci přecházet častěji; nicméně většina soutěžících stále nesprávně hodnotí pravděpodobnost úspěchu v 50:50.
Vos Savant a mediální rozruch
„Vyfoukl jsi to a pořádně jsi to vyhodil! Jelikož se zdá, že máš problémy s pochopením základního principu v práci, vysvětlím ti to. Poté, co hostitel odhalí kozu, máš nyní šanci jedna ke dvěma, že budeš správný. "Ať změníte svůj výběr nebo ne, šance jsou stejné. Matematická negramotnost je v této zemi dost a nepotřebujeme, aby se více šířilo nejvyšší IQ na světě. Hanba!"
Scott Smith, Ph.D. University of Florida
Vos Savant ve svém prvním sloupku o problému Monty Hall napsala, že by hráč měl změnit. Od svých čtenářů obdržela tisíce dopisů - drtivá většina z nich, včetně mnoha od čtenářů s doktoráty, s její odpovědí nesouhlasila. V letech 1990–1991 byly paradoxu věnovány další tři její sloupky v Parade . Četné příklady dopisů od čtenářů sloupků Vos Savant jsou prezentovány a diskutovány v The Monty Hall Dilemma: A Cognitive Illusion Par Excellence .
Diskuse byla přehrána na jiných místech (např. V novinovém sloupku Cecila Adamse „ The Straight Dope “) a byla uvedena ve velkých novinách, jako je The New York Times .
Ve snaze vyjasnit svou odpověď navrhla skořápkovou hru pro ilustraci: „Koukni se jinam a já pod jednu ze tří skořápek vložím hrášek. Poté tě žádám, abys položil prst na skořápku. Šance, které tvoje volba obsahuje hrach jsou 1/3, souhlasil? Potom jednoduše zvednu prázdnou skořápku ze zbývajících dvou dalších. Jelikož to mohu (a budu) dělat bez ohledu na to, co jste si vybrali, nedozvěděli jsme se nic, co by nám umožnilo revidovat šance na skořápce pod vaším prstem. “Navrhla také podobnou simulaci se třemi hracími kartami.
Vos Savant poznamenal, že i když některé nejasnosti byly způsobeny některými čtenáři aniž by si uvědomil, že měli předpokládat, že hostitel musí vždy odhalí kozu, téměř všechny její četné korespondenti bylo správně pochopil předpoklady problém, a ještě na počátku přesvědčeni, že vos Savant je odpověď („přepínač“) byla špatná.
Zmatek a kritika
Zdroje zmatku
Když se poprvé představí problém Monty Hall, drtivá většina lidí předpokládá, že každé dveře mají stejnou pravděpodobnost, a dospějí k závěru, že na přepnutí nezáleží. Z 228 subjektů v jedné studii se pouze 13% rozhodlo změnit. Ve své knize Síla logického myšlení , kognitivní psychologie Massimo Piattelli Palmarini píše: „Žádný jiný statistický puzzle přijde tak blízko k matení všemu lidu po celou dobu [i], i Nobel fyzici systematicky dát špatnou odpověď, a že trvají na tom a jsou připraveni nadávat tištěným těm, kteří navrhnou správnou odpověď. “ Holuby opakovaně vystavené tomuto problému ukazují, že se na rozdíl od lidí rychle naučí vždy přepínat.
Většina prohlášení o problému, zejména ta v Parade , neodpovídá pravidlům skutečné herní show a zcela nespecifikuje chování hostitele nebo to, že je náhodně vybrána poloha auta. Krauss a Wang se domnívají, že lidé dělají standardní předpoklady, i když nejsou výslovně uvedeny.
Ačkoli jsou tyto problémy matematicky významné, i při kontrole těchto faktorů si téměř všichni lidé stále myslí, že každé ze dvou neotevřených dveří má stejnou pravděpodobnost a dochází k závěru, že na přepnutí nezáleží. Tento předpoklad „stejné pravděpodobnosti“ je hluboce zakořeněná intuice. Lidé si silně myslí, že pravděpodobnost je rovnoměrně rozložena mezi tolik neznámých, kolik je jich přítomno, ať už je nebo není.
Problém nadále přitahuje pozornost kognitivních psychologů. Typické chování většiny, tj. Nepřepínání, lze vysvětlit jevy známými v psychologické literatuře jako:
- Dotace efekt , ve kterém lidé mají tendenci nadhodnocovat vítězné pravděpodobnosti již vybrán - už „ve vlastnictví“ - dveře.
- Status quo bias , ve kterém lidé raději držet s výběrem dveří, které již provedena.
- Chyby opomenutí vs. chyby provize, ve kterých, když jsou všechny ostatní věci stejné, lidé raději dělají chyby nečinností (Zůstaň) na rozdíl od akce (Přepínač).
Experimentální důkazy potvrzují, že se jedná o věrohodná vysvětlení, která nezávisí na intuici pravděpodobnosti. Další možností je, že intuice lidí jednoduše neřeší učebnicovou verzi problému, ale skutečné nastavení herní show. Existuje možnost, že velitel show bude klamat otevřením ostatních dveří, pouze pokud byly původně zvoleny dveře s autem. Ukázkový mistr hrající lstivě polovinu časů upravuje vítězné šance v případě, že je nabídnuto přepnutí na „stejnou pravděpodobnost“.
Kritika jednoduchých řešení
Jak již bylo uvedeno, většina zdrojů v oblasti pravděpodobnosti , včetně mnoha úvodních učebnic pravděpodobnosti, řeší problém ukázáním podmíněných pravděpodobností , že auto stojí za dveřmi 1 a dveřmi 21/3 a 2/3 (ne 1/2 a 1/2) vzhledem k tomu, že soutěžící nejprve vybere dveře 1 a hostitel otevře dveře 3; v předchozích pododdílech byly uvedeny různé způsoby, jak tento výsledek odvodit a porozumět mu.
Mezi těmito zdroji je několik, které výslovně kritizují populárně prezentovaná „jednoduchá“ řešení, přičemž říkají, že tato řešení jsou „správná, ale ... vratká“, nebo „neřeší daný problém“ nebo jsou „neúplná“ nebo „nepřesvědčivá a zavádějící “, nebo jsou (nejvíce otevřeně)„ nepravdivé “.
Sasha Voloch (2015) napsal, že „jakékoli vysvětlení, které říká něco jako„ pravděpodobnost dveří 1 byla 1/3„a nic to nemůže změnit ...“ je automaticky rybí: pravděpodobnosti jsou výrazy naší nevědomosti o světě a nové informace mohou změnit rozsah naší nevědomosti. “
Někteří říkají, že tato řešení odpovídají na trochu jinou otázku - jedna fráze zní „musíte před otevřením dveří oznámit, zda plánujete přepnout“.
Jednoduchá řešení různými způsoby ukazují, že soutěžící, který je odhodlán změnit, vyhraje auto s pravděpodobností 2/3, a tedy že přepínání je vítěznou strategií, pokud si hráč musí předem vybrat mezi „vždy přepínat“ a „vždy zůstat“. Pravděpodobnost výhry vždy přepnutím je však logicky odlišný koncept od pravděpodobnosti výhry přepnutím vzhledem k tomu, že si hráč vybral dveře 1 a hostitel otevřel dveře 3 . Jak říká jeden zdroj, „rozdíl mezi [těmito otázkami] zřejmě mnohé mate“. Skutečnost, že se liší, lze ukázat změnou problému tak, aby tyto dvě pravděpodobnosti měly různé číselné hodnoty. Předpokládejme například, že soutěžící ví, že Monty nevybírá druhé dveře náhodně mezi všemi legálními alternativami, ale místo toho, když dostane příležitost vybrat si mezi dvěma prohrávajícími dveřmi, Monty otevře ty napravo. V této situaci mají následující dvě otázky různé odpovědi:
- Jaká je pravděpodobnost, že vyhrajete auto tím, že vždy přepnete?
- Jaká je pravděpodobnost výhry auta, když si hráč vybral dveře 1 a hostitel otevřel dveře 3 ?
Odpověď na první otázku zní 2/3, jak správně ukazují „jednoduchá“ řešení. Ale odpověď na druhou otázku je nyní jiná: podmíněná pravděpodobnost, že se auto nachází za dveřmi 1 nebo dveřmi 2 vzhledem k tomu, že hostitel otevřel dveře 3 (dveře vpravo), je1/2. Důvodem je, že Montyho preference dveří úplně vpravo znamená, že otevře dveře 3, pokud je auto za dveřmi 1 (což je původně s pravděpodobností1/3) nebo pokud je auto za dveřmi 2 (také původně s pravděpodobností 1/3). U této varianty dvě otázky poskytují různé odpovědi. Dokud je však počáteční pravděpodobnost, že auto stojí za každými dveřmi, je1/3„Přepnout není nikdy na závadu soutěžícího, protože podmíněná pravděpodobnost výhry přepnutím je vždy minimálně 1/2.
V Morgan et al. , čtyři univerzitní profesoři publikovali článek v The American Statistician , který tvrdil, že vos Savant poskytl správnou radu, ale špatný argument. Věřili, že otázka položená na šanci auta za dveřmi 2 byla dána hráčovým počátečním výběrem dveří 1 a otevřených dveří 3, a ukázali, že tato šance je něco mezi1/2a 1 v závislosti na hostitelském rozhodovacím procesu daném výběru. Šance je jen tehdy, když je rozhodnutí zcela randomizované2/3.
V pozvaném komentáři a v následujících dopisech redaktorovi byli Morgan et al podporováni některými spisovateli, jinými kritizováni; v každém případě je odpověď Morgana a spol. zveřejněna společně s dopisem nebo komentářem v The American Statistician . Vos Savant se zejména energicky bránila. Morgan a kol. Si v reakci na vos Savant stěžovali, že vos Savant ve skutečnosti stále nereagoval na jejich vlastní hlavní bod. Později ve své odpovědi Hogbinovi a Nijdamovi souhlasili, že je přirozené předpokládat, že hostitel zvolí dveře, které se otevřou zcela náhodně, když má na výběr, a tedy že podmíněná pravděpodobnost výhry přepnutím (tj. podmíněné vzhledem k situaci, ve které se hráč nachází, když se musí rozhodnout) má stejnou hodnotu,2/3, jako bezpodmínečnou pravděpodobnost výhry přepnutím (tj. průměrem ze všech možných situací). Tuto rovnost zdůraznil již Bell (1992), který navrhl, aby matematicky zapojené řešení Morgana a spol. Oslovilo pouze statistiky, zatímco ekvivalence podmíněných a nepodmíněných řešení v případě symetrie byla intuitivně zřejmá.
V literatuře panuje neshoda ohledně toho, zda formulace vos Savantova problému, jak je uvedena v Parade , pokládá první nebo druhou otázku a zda je tento rozdíl významný. Behrends dochází k závěru, že „je třeba věc pečlivě zvážit, aby bylo vidět, že jsou obě analýzy správné“; což neznamená, že jsou stejní. Několik kritiků článku Morgana a kol. , jejíž příspěvky byly publikovány vedle původního příspěvku, kritizoval autory za to, že pozměnili formulaci vos Savantové a nesprávně interpretovali její záměr. Jeden diskutující (William Bell) považoval za věc vkusu, zda někdo výslovně uvede, že (za standardních podmínek), které dveře otevírá hostitel, nezávisí na tom, zda by měl člověk chtít přepnout.
Mezi jednoduchými řešeními se „řešení kombinovaných dveří“ nejvíce blíží podmíněnému řešení, jak jsme viděli v diskusi o přístupech využívajících koncept šancí a Bayesovu větu. Je založen na hluboce zakořeněné intuici, že odhalení již známých informací neovlivňuje pravděpodobnosti . Ale vědět, že hostitel může otevřít jedny ze dvou nevybraných dveří, aby ukázal kozu, neznamená, že by otevření konkrétních dveří nemělo vliv na pravděpodobnost, že auto bude za původně zvolenými dveřmi. Jde o to, že ačkoli předem víme, že hostitel otevře dveře a odhalí kozu, nevíme, které dveře otevře. Pokud hostitel zvolí náhodně jednotně mezi dveřmi skrývajícími kozu (jak je tomu ve standardní interpretaci), tato pravděpodobnost skutečně zůstane nezměněna, ale pokud si hostitel může mezi takovými dveřmi vybrat náhodně, pak konkrétní dveře, které hostitel otevře odhalí další informace. Hostitel může vždy otevřít dveře odhalující kozu a (ve standardní interpretaci problému) pravděpodobnost, že auto stojí za původně zvolenými dveřmi, se nemění, ale není to kvůli těm prvním, které jsou pravdivé. Řešení založená na tvrzení, že akce hostitele nemohou ovlivnit pravděpodobnost, že za původně zvoleným autem bude auto, vypadají přesvědčivě, ale toto tvrzení je jednoduše nepravdivé, pokud každá ze dvou možností hostitele není stejně pravděpodobná, pokud má na výběr. Tvrzení proto musí být odůvodněno; aniž by bylo uvedeno odůvodnění, je řešení přinejlepším neúplné. Odpověď může být správná, ale odůvodnění použité k jejímu odůvodnění je vadné.
Řešení využívající podmíněnou pravděpodobnost a další řešení
Výše uvedená jednoduchá řešení ukazují, že hráč se strategií přepínání vyhrává auto s celkovou pravděpodobností 2/3tj. bez ohledu na to, které dveře hostitel otevřel. Naproti tomu většina zdrojů v oblasti pravděpodobnosti vypočítává podmíněné pravděpodobnosti , že auto stojí za dveřmi 1 a dveřmi 21/3 a 2/3 vzhledem k tomu, že soutěžící zpočátku vybere dveře 1 a hostitel otevře dveře 3. Řešení v této části zohledňují pouze případy, kdy hráč vybral dveře 1 a hostitel otevřel dveře 3.
Upřesnění jednoduchého řešení
Pokud předpokládáme, že hostitel otevírá dveře náhodně, když má na výběr, pak které dveře hostitel otevře, nám neposkytne vůbec žádné informace o tom, zda je auto za dveřmi 1. V jednoduchých řešeních jsme již pozorovali že pravděpodobnost, že auto je za dveřmi 1, dveřmi původně zvolenými hráčem, je zpočátku 1/3. Kromě toho hostitel je jistě chystá otevřít se (jiný) dveře, takže otevření se dveře ( který dveře NS) se nemění to.1/3musí být průměrná pravděpodobnost, že auto je za dveřmi 1 vzhledem k hostitelským vybraným dveřím 2 a vzhledem k hostitelským vybraným dveřím 3, protože to jsou jediné dvě možnosti. Ale tyto dvě pravděpodobnosti jsou stejné. Proto jsou si oba rovni1/3. To ukazuje, že šance, že auto je za dveřmi 1, vzhledem k tomu, že hráč původně vybral tyto dveře a vzhledem k tomu, že hostitel otevřel dveře 3, je1/3, a z toho vyplývá, že šance, že auto je za dveřmi 2, vzhledem k tomu, že hráč původně vybral dveře 1 a hostitel otevřel dveře 3, je 2/3. Analýza také ukazuje, že celková úspěšnost2/3„Dosaženo vždy přepínáním , nelze vylepšit a zdůrazňuje to, co již mohlo být dobře intuitivně zřejmé: volba, před kterou stojí hráč, je, že mezi původně zvolenými dveřmi a druhými dveřmi, které hostitel nechal zavřené, jsou konkrétní čísla na těchto dveřích jsou irelevantní.
Podmíněná pravděpodobnost přímým výpočtem
Podle definice podmíněná pravděpodobnost výhry přepnutím vzhledem k tomu, že soutěžící zpočátku vybere dveře 1 a hostitel otevře dveře 3, je pravděpodobnost události „auto je za dveřmi 2 a hostitel otevře dveře 3“ děleno pravděpodobností „hostitel otevře dveře“ 3 ". Tyto pravděpodobnosti lze určit odkazem na níže uvedenou tabulku podmíněných pravděpodobností nebo na ekvivalentní rozhodovací strom, jak je znázorněno vpravo. Podmíněná pravděpodobnost výhry přepnutím je1/3/1/3 + 1/6, který je 2/3.
Níže uvedená tabulka podmíněných pravděpodobností ukazuje, jak by bylo 300 případů, ve kterých si hráč původně vybere dveře 1, rozděleno v průměru podle umístění auta a výběru dveří, které má hostitel otevřít.
Bayesova věta
Mnoho učebnic pravděpodobnosti a článků z oblasti teorie pravděpodobnosti odvozuje řešení podmíněné pravděpodobnosti formální aplikací Bayesovy věty ; mezi nimi knihy od Gilla a Henzeho. Použití pravděpodobnostní formy Bayesovy věty, často nazývané Bayesovým pravidlem, činí takové odvození transparentnějším.
Zpočátku je auto stejně pravděpodobné, že bude za některými ze tří dveří: šance na dveře 1, dveře 2 a dveře 3 jsou 1: 1: 1 . To platí i poté, co si hráč nezávislostí vybral dveře 1. Podle Bayesova pravidla jsou zadní šance na umístění vozu, vzhledem k tomu, že hostitel otevírá dveře 3, stejné jako předchozí šance vynásobené Bayesovým faktorem nebo pravděpodobností, což je podle definice pravděpodobnost nového kusu informací (hostitel otevírá dveře 3) pod každou z uvažovaných hypotéz (umístění vozu). Protože si hráč původně vybral dveře 1, šance, že hostitel otevře dveře 3, je 50%, pokud je auto za dveřmi 1, 100%, pokud je auto za dveřmi 2, 0%, pokud je auto za dveřmi 3. Tedy Bayesův faktor se skládá z poměrů1/2 : 1: 0 nebo ekvivalentně 1: 2: 0 , přičemž předchozí šance byly 1: 1: 1 . Tím se zadní šance vyrovnají Bayesovu faktoru 1: 2: 0 . Vzhledem k tomu, že hostitel otevřel dveře 3, je pravděpodobnost, že auto stojí za dveřmi 3, nulová a je dvakrát větší pravděpodobnost, že bude za dveřmi 2 než dveře 1.
Richard Gill analyzuje pravděpodobnost, že hostitel otevře dveře 3, následujícím způsobem. Vzhledem k tomu, že auto není za dveřmi 1, je stejně pravděpodobné, že je za dveřmi 2 nebo 3. Proto je šance, že hostitel otevře dveře 3, 50%. Vzhledem k tomu, že auto je za dveřmi 1, je šance, že hostitel otevře dveře 3, také 50%, protože když má hostitel možnost volby, je obě možnosti stejně pravděpodobné. Bez ohledu na to, zda je auto za dveřmi 1, je šance, že hostitel otevře dveře 3, 50%. Informace „hostitel otevírá dveře 3“ přispívá Bayesovým faktorem nebo poměrem pravděpodobnosti 1: 1 k tomu , zda je vůz za dveřmi 1. Zpočátku byla šance na dveře 1 skrývající auto 2: 1 . Proto zadní šance na dveře 1 skrývající auto zůstávají stejné jako předchozí šance, 2: 1 .
Stručně řečeno, informace o tom, které dveře otevírá hostitel (dveře 2 nebo dveře 3?), Neodhalí vůbec žádné informace o tom, zda je vůz za dveřmi 1, a právě to je údajně příznivci intuitivně zřejmé jednoduchá řešení, nebo pomocí frazémů matematických důkazů, „evidentně pravdivých, symetrií“.
Přímý výpočet
Zvažte událost Ci , která naznačuje, že auto stojí za dveřmi číslo i , má hodnotu Xi pro výběr hráče a hodnotu Hi pro hostitele, který otevírá dveře. Hráč si nejprve vybere dveře i = 1, C = X1 a hostitel otevře dveře i = 3, C = H3.
V tomto případě máme:
P (H3 | X1) = 1/2, protože tento výraz závisí pouze na X1 , nikoli na žádném Ci . V tomto konkrétním výrazu tedy výběr hostitele nezávisí na tom, kde je auto, a zbývají jen dvě dveře, jakmile je zvoleno X1 (například P (H1 | X1) = 0 ); a P (Ci, Xi) = P (Ci) P (Xi), protože Ci a Xi jsou nezávislé události (hráč neví, kde je auto, aby se mohl rozhodnout).
Pokud tedy hráč původně vybere dveře 1 a hostitel otevře dveře 3, dokážeme, že podmíněná pravděpodobnost výhry přepnutím je:
Z Bayesova pravidla víme, že P (A, B) = P (A | B) P (B) = P (B | A) P (A) . Rozšířením této logiky na více událostí, například A , B a C , získáme, že můžeme hrát s různými podmnožinami {A, B, C} a vypočítat pravděpodobnost průniku jako nástroj pro zjednodušení výpočtu našich podmíněná pravděpodobnost:
V našem případě, protože víme, že P (H3 | C2, X1) = 1 , máme štěstí:
Řešení strategické dominance
Když se vrátíme do Nalebuffu, problém Monty Hall je také hodně studován v literatuře o teorii her a teorii rozhodování a tomuto pohledu také odpovídají některá populární řešení. Vos Savant žádá o rozhodnutí, ne o šanci. A náhodné aspekty toho, jak je auto skryté a jak se otevírají nevybrané dveře, nejsou známy. Z tohoto úhlu pohledu je třeba mít na paměti, že hráč má dvě možnosti, jak se rozhodnout: za prvé, které dveře si na začátku zvolí; a za druhé, zda přepnout či nikoli. Protože neví, jak je auto ukryté ani jak se hostitel rozhoduje, možná bude moci využít příležitosti své první volby, jako by neutralizoval akce týmu, který vede kvízovou show, včetně hostitele.
Po Gillovi zahrnuje strategie soutěžícího dvě akce: počáteční výběr dveří a rozhodnutí se přepnout (nebo se držet), což může záviset jak na původně vybraných dveřích, tak na dveřích, na které hostitel nabízí přepnutí. Strategií jednoho soutěžícího je například „vybrat dveře 1, poté přepnout na dveře 2, když jsou nabídnuty, a nepřepnout na dveře 3, když jsou nabídnuty“. Existuje dvanáct takových deterministických strategií soutěžícího.
Elementární srovnání strategií soutěžících ukazuje, že pro každou strategii A existuje další strategie B „vyberte dveře, pak se přepněte, ať se stane cokoli“, která jim dominuje. Bez ohledu na to, jak je auto skryté a bez ohledu na to, jaké pravidlo hostitel používá, když má na výběr mezi dvěma kozami, pokud A vyhraje auto, pak také B. Například strategii A „vybrat dveře 1, pak se jí vždy držet“ dominuje strategie B „vybrat dveře 1 a poté vždy přepnout poté, co hostitel odhalí dveře“: A vyhraje, když dveře 1 skryjí auto, zatímco B vyhraje, když jeden dveří 2 a 3 zakrývá auto. Podobně strategii A „vyberte dveře 1, poté přepněte na dveře 2 (je -li nabízeno), ale nepřepínejte na dveře 3 (je -li nabízeno)“ dominuje strategie B „vyberte dveře 3, pak vždy přepněte“.
Dominance je silným důvodem k hledání řešení mezi neustále se měnícími strategiemi za poměrně obecných předpokladů o prostředí, ve kterém se soutěžící rozhoduje. Zejména pokud je auto skryto pomocí nějakého randomizačního zařízení-jako je házení symetrickými nebo asymetrickými třístrannými kostkami-dominance znamená, že strategie maximalizující pravděpodobnost výhry automobilu bude mezi třemi strategiemi, které se vždy mění. být strategií, která zpočátku vybírá nejméně pravděpodobné dveře, pak se přepne bez ohledu na to, které dveře k přepnutí nabízí hostitel.
Strategická dominance spojuje problém Monty Hall s teorií her . V nastavení hry Gill s nulovým součtem vyřazení nepřepínacích strategií redukuje hru na následující jednoduchou variantu: hostitel (nebo televizní tým) se rozhodne, že dveře skryje auto, a soutěžící si vybere dvoje dveře ( tj. dvoje dveře zbývající po první, nominální, volbě hráče). Soutěžící vyhrává (a její soupeř prohrává), pokud je auto za jedněmi ze dvou dveří, které si vybrala.
Řešení simulací
Jednoduchý způsob, jak ukázat, že strategie přepínání skutečně vyhrává dvakrát ze tříkrát za standardních předpokladů, je simulovat hru pomocí hracích karet . Tři karty z obyčejného balíčku představují tři dveře; jedna 'speciální' karta představuje dveře s autem a dvě další karty představují kozí dveře.
Simulaci lze několikrát opakovat a simulovat více kol hry. Hráč si vybere jednu ze tří karet a poté při pohledu na zbývající dvě karty „hostitel“ odhodí kartu kozu. Pokud je v ruce hostitele karta automobilu, je to zaznamenáno jako výhra při změně; drží -li hostitel kozí kartu, je kolo zaznamenáno jako setrvající výhra. Protože se tento experiment opakuje v několika kolech, pozorovaná míra výhry pro každou strategii se pravděpodobně přiblíží její teoretické pravděpodobnosti výhry v souladu se zákonem velkého počtu .
Opakované hraní také objasňuje, proč je přepínání lepší strategií. Poté, co si hráč vezme svou kartu, je již určeno, zda přepnutí vyhraje kolo pro hráče. Pokud to není přesvědčivé, simulaci lze provést s celým balíčkem. V této variantě je vůz karta jde do hostitelského 51 případech z 52, jakož i pobyty s hostiteli bez ohledu na to, kolik non jsou -auto karty zahodí.
Varianty
Běžná varianta problému, kterou několik akademických autorů považuje za kanonický problém, neznamená zjednodušující předpoklad, že hostitel musí jednotně zvolit dveře, které se mají otevřít, ale že použije jinou strategii . Zmatek ohledně toho, jaká formalizace je autoritativní, vedl ke značné ostrosti, zejména proto, že tato varianta činí důkazy více zapojenými, aniž by se změnila optimalita strategie vždy přepínat pro hráče. V této variantě může mít hráč různé pravděpodobnosti výhry v závislosti na pozorovaném výběru hostitele, ale v každém případě je pravděpodobnost výhry přepnutím minimálně1/2(a může být až 1), přičemž celková pravděpodobnost výhry přepnutím je stále přesně2/3. Varianty jsou někdy prezentovány postupně v učebnicích a článcích určených k výuce základů teorie pravděpodobnosti a teorie her . Byl studován také značný počet dalších zobecnění.
Jiné chování hostitele
Verze problému Monty Hall publikovaná v Parade v roce 1990 konkrétně neuváděla, že hostitel vždy otevře další dveře, nebo vždy nabídne možnost přepnutí, nebo dokonce nikdy neotevře dveře odhalující auto. Vos Savantová však ve svém druhém sledovacím sloupci jasně uvedla, že chování zamýšleného hostitele může být pouze tím, co vedlo k2/3pravděpodobnost, kterou dala jako svou původní odpověď. „Cokoli jiného je jiná otázka.“ „Prakticky všichni mí kritici rozuměli zamýšlenému scénáři. Osobně jsem přečetl téměř tři tisíce dopisů (z mnoha dalších tisíců, které přišly) a téměř každý z nich trval na tom, že jednoduše protože dvě možnosti zůstaly (nebo ekvivalentní chyba), šance byla dokonce. Velmi málo vznesených otázek ohledně nejasností a dopisy skutečně zveřejněné ve sloupci mezi těmi několika nebyly. “ Odpověď následuje, pokud je vůz umístěn náhodně za jakýmikoli dveřmi, hostitel musí otevřít dveře odhalující kozu bez ohledu na počáteční volbu hráče, a pokud jsou k dispozici dvě dveře, zvolí, které z nich se otevře náhodně. Níže uvedená tabulka ukazuje řadu dalších možných chování hostitele a dopad na úspěch přepnutí.
Určení nejlepší strategie hráče v rámci daného souboru dalších pravidel, která musí hostitel dodržovat, je typem problému studovaného v teorii her . Pokud například hostitel nemusí předložit nabídku k přepnutí, hráč může mít podezření, že hostitel je škodlivý, a nabídky dělá častěji, pokud si hráč původně vybral auto. Odpověď na tento druh otázek obecně závisí na konkrétních předpokladech o chování hostitele a může se pohybovat od „zcela ignorovat hostitele“ až po „hodit mincí a změnit, pokud se objeví“; viz poslední řádek tabulky níže.
Morgan et al a Gillman ukazují obecnější řešení, kde je auto (rovnoměrně) umístěno náhodně, ale hostitel není nucen vybírat rovnoměrně náhodně, pokud si hráč auto původně vybral, což je způsob, jakým oba interpretují tvrzení o problému v Parade navzdory autorovým odmítnutím odpovědnosti. Oba změnili znění verze Parade, aby zdůraznili ten bod, když problém zopakovali. Uvažují o scénáři, kdy hostitel volí mezi odhalením dvou koz s preferencí vyjádřenou jako pravděpodobnost q , která má hodnotu mezi 0 a 1. Pokud hostitel náhodně vybere q, bude1/2 a přepínání výher s pravděpodobností 2/3bez ohledu na to, jaké dveře hostitel otevře. Pokud hráč vybere dveře 1 a hostitel upřednostní dveře 3, je q , pak pravděpodobnost, že hostitel otevře dveře 3 a auto je za dveřmi 2, je1/3, zatímco pravděpodobnost, že hostitel otevře dveře 3 a auto je za dveřmi 1, je q/3. Toto jsou jediné případy, kdy hostitel otevře dveře 3, takže podmíněná pravděpodobnost výhry přepnutím vzhledem k tomu, že hostitel otevře dveře 3, je1/3/1/3 + q /3 což zjednodušuje na 1/1 + q. Protože q se může pohybovat mezi 0 a 1, může se tato podmíněná pravděpodobnost měnit mezi1/2a 1. To znamená, že i když hráč nenutí hosta náhodně vybírat, pokud si hráč zpočátku vybere auto, není na tom hráč nikdy hůře. Nicméně ani jeden zdroj nenaznačuje, že hráč ví, jaká je hodnota q, takže hráč nemůže přiřadit jinou pravděpodobnost než2/3 které vos Savant považoval za implicitní.
| Možné chování hostitele při nespecifikovaném problému | |
|---|---|
| Chování hostitele | Výsledek |
| Hostitel se chová tak, jak je uvedeno v konkrétní verzi problému. | Přepnutí vyhrává auto ve dvou třetinách času. (Specifický případ generalizovaného formuláře níže s p = q = 1/2) |
| Hostitel vždy odhalí kozu a vždy nabídne přepínač. Pokud má na výběr, vybere si kozu úplně vlevo s pravděpodobností p (což může záviset na počátečním výběru hráče) a dveře úplně vpravo s pravděpodobností q = 1 - p . | Pokud hostitel otevře dveře úplně vpravo, přepnutí vyhrává s pravděpodobností 1/(1+ q ). |
| „Monty from Hell“: Host nabízí možnost přepnout pouze v případě, že počáteční volbou hráče jsou vítězné dveře. | Přepnutí vždy přinese kozu. |
| „Monty-reading Monty“: Host nabízí možnost přepnutí v případě, že se host rozhodne zůstat tak jako tak, nebo v případě, že host přejde na kozu. | Přepnutí vždy přinese kozu. |
| „Angelic Monty“: Hostitel nabízí možnost přepnout, pouze pokud si hráč vybral nesprávně. | Přepnutí vždy vyhrává auto. |
| „Monty Fall“ nebo „Ignorant Monty“: Host neví, co se skrývá za dveřmi, a náhodně otevře ten, který náhodou neodhalí auto. | Přepnutí vyhrává auto polovinu času. |
| Hostitel ví, co se skrývá za dveřmi, a (před volbou hráče) náhodně vybere, kterou kozu odhalí. Nabízí možnost přepnout pouze tehdy, když se výběr hráče liší od jeho. | Přepnutí vyhrává auto polovinu času. |
| Hostitel otevře dveře a nabídne 100% přepnutí, pokud si soutěžící původně vybral auto, a 50% čas jinak. | Přepínání vyhrává 1/2čas v Nashově rovnováze . |
| Čtyřstupňová teoretická hra pro dva hráče. Hráč hraje proti pořadatelům pořadu (televizní stanice), jehož součástí je hostitel. První fáze: Organizátoři si vyberou dveře (volba je před hráčem utajena). Druhá fáze: hráč provede předběžnou volbu dveří. Třetí fáze: hostitel otevírá dveře. Čtvrtá fáze: hráč učiní konečnou volbu. Hráč chce vyhrát auto, televizní stanice si ho chce nechat. Jedná se o hru pro dvě osoby s nulovým součtem. Podle von Neumannovy věty z teorie her , pokud oběma stranám dovolíme plně randomizované strategie, existuje řešení minimaxu nebo Nashova rovnováha . | Řešení Minimax ( Nashova rovnováha ): auto se nejprve náhodně skryje rovnoměrně a hostitel později zvolí jednotné náhodné dveře, které se otevřou, aniž by odhalily auto, a liší se od dveří hráče; hráč nejprve zvolí jednotné náhodné dveře a později vždy přepne na jiné zavřené dveře. Se svou strategií má hráč minimálně šanci na výhru2/3, nicméně televizní stanice hraje; se strategií televizní stanice bude televizní stanice prohrávat maximálně s pravděpodobností2/3hráč však hraje. Skutečnost, že se tyto dvě strategie shodují (minimálně2/3, nejvíce 2/3) dokazuje, že tvoří řešení minimax. |
| Jako dříve, ale nyní má hostitel možnost neotevřít dveře vůbec. | Řešení Minimax ( Nashova rovnováha ): auto je nejprve náhodně skryto rovnoměrně a hostitel později nikdy neotevře dveře; hráč si nejprve vybere dveře rovnoměrně náhodně a později se nikdy nepřepne. Hráčova strategie zaručuje minimálně šanci na výhru1/3. Strategie televizní stanice zaručuje ztrátu šance maximálně1/3. |
| Případ Deal or No Deal : hostitel požádá hráče, aby otevřel dveře, a poté nabídne spínač v případě, že auto nebylo odhaleno. | Přepnutí vyhrává auto polovinu času. |
N dveře
DL Ferguson (1975 v dopise Selvinovi ) navrhuje N -dveře zobecnění původního problému, ve kterém hostitel otevírá p ztrácí dveře a poté nabízí hráči možnost přepnout; v této variantě přepínání vítězí s pravděpodobností . Tato pravděpodobnost je vždy větší než , proto přepínání vždy přináší výhodu.
I když hostitel otevře pouze jedny dveře ( ), hráč se v každém případě lépe přepne. Jak se N zvětšuje, výhoda klesá a blíží se nule. Na druhé straně, pokud hostitel otevře všechny prohrávající dveře kromě jednoho ( p = N - 2), výhoda se zvyšuje s tím, jak N roste (pravděpodobnost výhry přepnutím jeN - 1/N., který se blíží 1, protože N roste velmi velký).
Kvantová verze
Kvantová verze paradoxu ukazuje některé body o vztahu mezi klasickou nebo nekvantovou informací a kvantovou informací , zakódované ve stavech kvantově mechanických systémů. Formulace je volně založená na kvantové teorii her . Tři dveře jsou nahrazeny kvantovým systémem umožňujícím tři alternativy; otevření dveří a nahlédnutí za ně je přeloženo jako provedení konkrétního měření. V tomto jazyce mohou být stanovena pravidla a opět je pro hráče volbou zůstat u původní volby nebo přejít na jinou „ortogonální“ možnost. Druhá strategie ukazuje, že zdvojnásobuje šance, stejně jako v klasickém případě. Pokud však hostitel přehlídky nerozhodl polohu ceny zcela kvantově mechanicky, hráč to zvládne ještě lépe a někdy dokonce může cenu s jistotou vyhrát.
Dějiny
Nejdříve z několika pravděpodobnostních hádanek souvisejících s problémem Monty Hall je Bertrandův paradox boxu , který položil Joseph Bertrand v roce 1889 ve svém Calcul des probabilités . V této logické hře jsou tři krabice: krabice obsahující dvě zlaté mince, krabice se dvěma stříbrnými mincemi a krabice s jednou z nich. Po náhodném výběru krabice a náhodném výběru jedné mince, která je shodou okolností zlatá, je otázkou, jaká je pravděpodobnost, že druhá mince je zlatá. Stejně jako v problému Monty Hall je intuitivní odpověď1/2, ale pravděpodobnost ve skutečnosti je 2/3.
Three Vězni problém , publikoval v Martin Gardner ‚s Matematické hry sloupce v časopise Scientific American v roce 1959 je ekvivalentní k problému Monty Hall. Tento problém zahrnuje tři odsouzené vězně, z nichž jeden byl tajně vybrán, aby byl omilostněn. Jeden z vězňů prosí dozorce, aby mu sdělil jméno jednoho z ostatních, kteří mají být popraveni, s argumentem, že to neodhalí žádné informace o jeho vlastním osudu, ale zvyšuje to jeho šance na odpuštění1/3 na 1/2. Správce je povinen (tajně) hodit mincí, aby rozhodl, jaké jméno poskytne, pokud je vězeň, který žádá, ten, komu je odpuštěno. Otázkou je, zda znalost dozorceho odpovědi mění šance vězně na milost. Tento problém je ekvivalentní problému Monty Hall; vězeň pokládající otázku stále má1/3 šance na milost, ale jeho nejmenovaný kolega má 2/3 šance.
Steve Selvin položil problém Monty Hall ve dvojici dopisů The American Statistician v roce 1975. První dopis představil problém ve verzi blízké jeho představení v Parade o 15 let později. Druhý se zdá být prvním použitím výrazu „problém Monty Hall“. Problém je ve skutečnosti extrapolací z herní show. Monty Hall dělal otevřela špatné dveře k vybudování vzrušení, ale nabídl známou nižší cenu - například 100 as $ v hotovosti - spíše než výběr pro přepnutí dveří. Jak napsal Monty Hall Selvinovi:
A pokud se někdy dostanete na mou show, pravidla pro vás platí rychle - po výběru žádné obchodní boxy.
- Monty Hall
Verze problému velmi podobná té, která se objevila o tři roky později v Parade, byla zveřejněna v roce 1987 v sekci Puzzles v The Journal of Economic Perspectives . Nalebuff, jako pozdější spisovatelé v matematické ekonomii, vidí problém jako jednoduché a zábavné cvičení v teorii her .
„The Monty Hall Trap“, článek Phillipa Martina z roku 1989 v Bridge Today , představil Selvinův problém jako příklad toho, co Martin nazývá pravděpodobnostní pastí zacházení s náhodnými informacemi, jako by byly náhodné, a vztahuje to k pojmům ve hře Bridge. .
Přepracovány verze Selvin se problém objevil v Marilyn vos Savantová ‚S Zeptejte se Marilyn otázek a odpovědí sloupec Parade v září 1990. Ačkoli vos Savant dával správnou odpověď, že přepínání by vyhrát dvě třetiny času, ona odhaduje časopis obdržel 10 000 dopisů včetně téměř 1 000 podepsaných doktorandy, mnoho z nich na hlavičkových papírech matematických a přírodovědných oddělení, prohlašujících, že její řešení bylo špatné. Vzhledem k drtivé reakci Parade publikoval na tento problém nevídané čtyři sloupce. V důsledku publicity si problém vysloužil alternativní název „Marilyn a kozy“.
V listopadu 1990 proběhla stejně svárlivá diskuse o článku vos Savanta ve sloupku Cecila Adamse „ Rovná droga “. Adams zpočátku odpověděl nesprávně, že šance na zbývající dvě dveře musí být každá jedna. Poté, co čtenář napsal, aby opravil matematiku Adamsovy analýzy, Adams souhlasil, že se matematicky mýlil. „Vyberete si dveře č. 1. Nyní vám bude nabídnuta tato volba: otevřené dveře č. 1 nebo otevřené dveře č. 2 a dveře č. 3. V druhém případě si cenu necháte, pokud je za některými dveřmi. Raději byste měli dva na tři střílí na cenu než jeden na tři, nemyslíte? Když se nad tím zamyslíte, původní problém vám nabízí v podstatě stejnou možnost. Monty ve skutečnosti říká: můžete si nechat jedny dveře nebo můžeš mít další dvoje dveře, z nichž jedny (dveře bez ceny) ti otevřu. “ Adams řekl, že verze Parade ponechala kritická omezení neuvedená a bez těchto omezení nebyly šance na výhru přepnutím nutně dvě ze tří (např. Nebylo rozumné předpokládat, že hostitel vždy otevře dveře). Řada čtenářů však napsala, že tvrdí, že Adams měl „poprvé pravdu“ a že správná šance byla jedna ku dvěma.
Parade sloup a jeho reakce věnována značná pozornost v tisku, včetně titulní straně článek v New York Times , v němž Monty Hall sám byl dotazován. Hall problém pochopil, reportérovi předvedl ukázku s klíči od auta a vysvětlil, jak se skutečná hra na Let's Make a Deal liší od pravidel logické hry. V článku Hall poukázal na to, že protože měl kontrolu nad tím, jak hra postupuje, hraje na psychologii soutěžícího, teoretické řešení se nevztahovalo na skutečnou hru přehlídky. Řekl, že ho nepřekvapilo naléhání odborníků, že pravděpodobnost je 1 ze 2. „To je stejný předpoklad, který by soutěžící v pořadu udělali poté, co jsem jim ukázal, že za jedněmi dveřmi nic není,“ řekl. „Mysleli by si, že šance na jejich dveřích se nyní zvýšila na 1 ku 2, a tak neradi se vzdali dveří bez ohledu na to, kolik peněz jsem nabídl. Otevřením těch dveří jsme vyvíjeli tlak. Říkali jsme tomu Henry James Bylo to „ otočení šroubu “. " Hall objasnil, že jako hostitel herní show nemusel dodržovat pravidla hádanky ve sloupci vos Savant a nemusel vždy umožnit člověku příležitost přepnout (např. Mohl by jim okamžitě otevřít dveře, pokud by to byl ztrácí dveře, může jim nabídnout peníze, aby nepřešli z prohrávajících dveří na vítězné dveře, nebo jim může umožnit možnost přepnout pouze v případě, že mají vítězné dveře). „Pokud je hostitel povinen neustále otevírat dveře a nabízet vám vypínač, měli byste jej přepnout,“ řekl. „Ale pokud má na výběr, zda povolí přechod, nebo ne, pozor. Caveat emptor. Vše závisí na jeho náladě.“
Viz také
- MythBusters Episode 177 „Wheel of Mythfortune“ - Vyberte si dveře
- Princip omezené volby - podobná aplikace bayesovské aktualizace v kontraktovém můstku
Podobné hádanky v teorii pravděpodobnosti a rozhodování
Reference
Bibliografie
- Adams, Cecil (2. listopadu 1990). „Na Let's Make a Deal vyberete dveře č. 1. Monty otevírá dveře č. 2 - žádná cena. Zůstanete u dveří č. 1 nebo přejdete na č. 3?“ . Rovná droga . Citováno 25. července 2005 .
- Barbeau, Edward (1993). „Klamů, vad a Flimflam: Problém auta a koz“. The College Mathematics Journal . 24 (2): 149–154. doi : 10,1080/07468342.1993.11973519 .
- Behrends, Ehrhard (2008). Pětiminutová matematika . Knihkupectví AMS. p. 57. ISBN 978-0-8218-4348-2.
- Bell, William (srpen 1992). „Komentář k Pojďme se domluvit Morganem a spol. “. Americký statistik . 46 (3): 241.
- Carlton, Matthew (2005). „Rodokmeny, ceny a vězni: Zneužití podmíněné pravděpodobnosti“ . Journal of Statistics Education . 13 odst. doi : 10.1080/10691898.2005.11910554 . S2CID 118792491 .
- Chun, Young H. (1991). „Problém s ukázkou hry“. NEBO MS dnes . 18 (3): 9.
- D'Ariano, GM; Gill, RD; Keyl, M .; Kuemmerer, B .; Maassen, H .; Werner, RF (21. února 2002). „Problém Quantum Monty Hall“. Kvant. Inf. Výpočet . 2 (5): 355–366. arXiv : quant-ph/0202120 . Bibcode : 2002quant.ph..2120D .
- Devlin, Keith (červenec – srpen 2003). „Devlinův úhel: Monty Hall“ . Matematická asociace Ameriky . Citováno 23. června 2014 .
- Devlin, Keith (prosinec 2005). „Devlinův úhel: Monty Hall se vrátil“ . Matematická asociace Ameriky . Citováno 23. června 2014 .
- Eisenhauer, Joseph G. (2001). „Matice Monty Hall“ (PDF) . Výuka statistiky . 22 (1): 17–20. doi : 10,1111/1467-9639.00005 . Archivováno z originálu (PDF) dne 1. března 2012 . Vyvolány 9 July 2012 .
- Enßlin, Torsten A .; Westerkamp, Margret (duben 2018). „Racionalita iracionality v problému Monty Hall“. Annalen der Physik . 531 (3): 1800128. arXiv : 1804.04948 . Bibcode : 2019AnP ... 53100128E . doi : 10.1002/andp.201800128 . S2CID 56036255 .
- Falk, Ruma (1992). „Bližší pohled na pravděpodobnosti notoricky známých tří vězňů“. Poznání . 43 (3): 197–223. doi : 10,1016/0010-0277 (92) 90012-7 . PMID 1643813 . S2CID 39617738 .
- Flitney, Adrian P. & Abbott, Derek (2002). „Kvantová verze problému Monty Hall“. Fyzická Aktualizace . 65 (6): 062318. arXiv : quant-ph/0109035 . Bibcode : 2002PhRvA..65f2318F . doi : 10,1103/PhysRevA.65.062318 . S2CID 119417490 . Umění. Č. 062318, 2002.
- Fox, Craig R. & Levav, Jonathan (2004). „Partition-Edit-Count: Naive Extensional Reasoning in Judgment of Conditional Probability“ (PDF) . Journal of Experimental Psychology: General . 133 (4): 626–642. doi : 10,1037/0096-3445.133.4.626 . PMID 15584810 . Archivováno z originálu (PDF) dne 10. dubna 2020.
- Gardner, Martin (říjen 1959a). „Matematické hry“. Scientific American : 180–182. Přetištěno ve Druhé vědecké americké knize matematických hádanek a odklonůCS1 maint: postscript ( odkaz )
- Gardner, Martin (listopad 1959b). „Matematické hry“. Scientific American : 188.
- Gardner, Martin (1982). Aha! Gotcha: Paradoxy k hádankám a potěšení . WH Freeman. ISBN 978-0716713616.
- Gill, Jeff (2002). Bayesovské metody . Stiskněte CRC. s. 8–10. ISBN 1-58488-288-3. ( omezená online kopie , str. 8, v Knihách Google )CS1 maint: postscript ( odkaz )
- Gill, Richard (2010). „Problém Monty Hall“. Mezinárodní encyklopedie statistických věd . Springer. s. 858–863. arXiv : 1002,3878v2 .
- Gill, Richard (únor 2011). „Problém Monty Hall není hádankou pravděpodobnosti (je to výzva v matematickém modelování)“. Statistica Neerlandica . 65 (1): 58–71. arXiv : 1002.0651v3 . doi : 10.1111/j.1467-9574.2010.00474.x .
- Gill, Richard (17. března 2011a). „Problém Monty Hall“ (PDF) . Matematický institut, University of Leiden, Nizozemsko. s. 10–13.
- Gillman, Leonard (1992). „Auto a kozy“. American Mathematical Monthly . 99 (1): 3–7. doi : 10,2307/2324540 . JSTOR 2324540 .
- Gilovich, T .; Medvec, VH & Chen, S. (1995). „Provize, opomenutí a snížení disonance: Vyrovnání se s lítostí v problému„ Monty Hall “. Časopis osobnosti a sociální psychologie . 21 (2): 182–190. doi : 10,1177/0146167295212008 . S2CID 146500989 .
- Gnedin, Sasha (2011). „Hra Mondee Gills“ . Matematický zpravodaj . 34 : 34–41. doi : 10,1007/s00283-011-9253-0 .
- Granberg, Donald (2014). Dilema Monty Hall: Kognitivní iluze Par Excellence . Lumad/CreateSpace. ISBN 978-0996100809.
- Granberg, Donald (1996). „Přepnout nebo nepřepnout“. Ve vos Savant, Marilyn (ed.). Síla logického myšlení . Svatomartinský tisk. ISBN 0-312-30463-3. ( omezená online kopie , str. 169, v Knihách Google )CS1 maint: postscript ( odkaz )
- Granberg, Donald & Brown, Thad A. (1995). „Dilema Monty Hall“. Bulletin osobnosti a sociální psychologie . 21 (7): 711–729. doi : 10,1177/0146167295217006 . S2CID 146329922 .
- Grinstead, Charles M. & Snell, J. Laurie (4. července 2006). Úvod Grinsteada a Snella do pravděpodobnosti (PDF) . Citováno 2. dubna 2008 .
- Hall, Monty (1975). „Problém Monty Hall“ . LetsMakeADeal.com . Citováno 15. ledna 2007 . Obsahuje dopis z 12. května 1975 Stevu SelvinoviCS1 maint: postscript ( odkaz )
- Henze, Norbert (2011) [1997]. Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls (9. vydání). Springer. s. 50–51, 105–107. ISBN 978-3834818454. ( omezená kopie online , str. 105, v Knihách Google )CS1 maint: postscript ( odkaz )
- Herbranson, WT & Schroeder, J. (2010). "Jsou ptáci chytřejší než matematici? Holuby ( Columba livia ) fungují optimálně s verzí dilema Monty Hall" . Časopis srovnávací psychologie . 124 (1): 1–13. doi : 10,1037/a0017703 . PMC 3086893 . PMID 20175592 .
- Hogbin, M .; Nijdam, W. (2010). „Dopis redaktorovi na Pojďme se dohodnout od Morgana a spol. “. Americký statistik . 64 (2): 193. doi : 10,1198/tast.2010.09227 . S2CID 219595003 .
- Kahneman, D .; Knetsch, JL & Thaler, RH (1991). „Anomálie: Nadační efekt, averze ke ztrátě a zaujatost vůči status quo“ . Journal of Economic Perspectives . 5 : 193–206. doi : 10,1257/jep.5.1.193 .
- Kaivanto, K .; Kroll, EB & Zabinski, M. (2014). „Manipulace s předpětím spouštění a porozumění úkolu v Monty Hall“ (PDF) . Ekonomický zpravodaj . 34 (1): 89–98.
- Krauss, Stefan & Wang, XT (2003). „Problém psychologie Montyho Halla: Objevování psychologických mechanismů pro řešení houževnatého hlavolamu“ (PDF) . Journal of Experimental Psychology: General . 132 (1): 3–22. doi : 10,1037/0096-3445.132.1.3 . Citováno 30. března 2008 .
- Lucas, Stephen; Rosenhouse, Jason & Schepler, Andrew (2009). „Problém Monty Hall, přehodnoceno“ (PDF) . Matematický časopis . 82 (5): 332–342. doi : 10,4169/002557009X478355 . Získaný 9. července 2012 .
- Martin, Phillip (1993) [1989]. Granovetter, Pamela; Granovetter, Matthew (eds.). Past Monty Hall . Pouze pro odborníky . Granovetterovy knihy.
- Morgan, JP; Chaganty, NR; Dahiya, RC & Doviak, MJ (1991). „Pojďme se domluvit: dilema hráče“. Americký statistik . 45 (4): 284–287. doi : 10,1080/00031305.1991.10475821 . JSTOR 2684453 .
- Morone, A. & Fiore, A. (2007). „Tři dveře Montyho Halla pro atrapy“ . Dipartimento di Scienze Economiche e Metodi Matematici - Università di Bari, Southern Europe Research in Economic Studies - SERIES Working Paper no. 0012.
- Mueser, Peter R. & Granberg, Donald (květen 1999). „Monty Hall Dilemma Revisited: Pochopení interakce definice problému a rozhodování“ . Experimentální . Univerzitní knihovna v Mnichově. Pracovní dokument 99–06 . Vyvolány 10 June 2010 .
- Nalebuff, Barry (podzim 1987). „Puzzle: Vyberte si oponu, Duel-ity, dvoubodové převody a další“ . Journal of Economic Perspectives . 1 (2): 157–163. doi : 10,1257/jep.1.2.157 .
- Rao, M. Bhaskara (srpen 1992). „Komentář k Pojďme se dohodnout od Morgana a spol. “. Americký statistik . 46 (3): 241–242.
- Rosenhouse, Jason (2009). Problém Monty Hall . Oxford University Press. ISBN 978-0-19-536789-8.
- Rosenthal, Jeffrey S. (září 2005a). „Monty Hall, Monty Fall, Monty Crawl“ (PDF) . Math Horizons : 5-7.
- Rosenthal, Jeffrey S. (2005b). Zasažen bleskem: Zvědavý svět pravděpodobností . Harper Collins. ISBN 978-0-00-200791-7.
- Samuelson, W. & Zeckhauser, R. (1988). „Zachycení současného stavu při rozhodování“. Žurnál rizika a nejistoty . 1 : 7–59. CiteSeerX 10.1.1.632.3193 . doi : 10,1007/bf00055564 . S2CID 5641133 .
- Selvin, Steve (únor 1975a). „Problém v pravděpodobnosti (dopis redakci)“. Americký statistik . 29 (1): 67–71. doi : 10,1080/00031305.1975.10479121 . JSTOR 2683689 .
- Selvin, Steve (srpen 1975b). „K problému Monty Hall (dopis redaktorovi)“. Americký statistik . 29 (3): 134. JSTOR 2683443 .
- Seymann, RG (1991). „Komentář k Pojďme se dohodnout : dilema hráče“. Americký statistik . 45 (4): 287–288. doi : 10,2307/2684454 . JSTOR 2684454 .
- Stibel, Jeffrey ; Dror, Itiel; Ben-Zeev, Talia (2008). „The Collapsing Choice Theory: Dissociating Choice and Judgment in decision Making“ (PDF) . Teorie a rozhodnutí .
- Tierney, John (21. července 1991). „Za dveřmi Montyho Halla: Puzzle, debata a odpověď?“ . The New York Times . Citováno 18. ledna 2008 .
- Vazsonyi, Andrew (prosinec 1998 - leden 1999). „Které dveře má Cadillac?“ (PDF) . Rozhodovací linie : 17–19. Archivováno z originálu (PDF) dne 2014-04-13 . Citováno 16. října 2012 .Údržba CS1: datum a rok ( odkaz )
- VerBruggen, Robert (24. února 2015). „Problém„ Monty Hall “: Všichni se mýlí“ . RealClearScience . Citováno 2017-10-12 .
- Volokh, Sasha (02.03.2015). „Snadná odpověď na neslavný problém Monty Hall“ . Washington Post . ISSN 0190-8286 . Citováno 2017-10-12 .
- vos Savant, Marilyn (2012) [1990–1991]. „Problém s ukázkou hry“ . Průvod . Archivovány od originálu dne 29. dubna 2012.
- vos Savant, Marilyn (9. září 1990a). „Zeptej se Marilyn“ . Průvod : 16. Archivováno od originálu dne 21. ledna 2013 . Vyvolány 12 November 2012 .
- vos Savant, Marilyn (2. prosince 1990b). „Zeptej se Marilyn“ . Průvod : 25. Archivováno od originálu dne 21. ledna 2013 . Vyvolány 12 November 2012 .
- vos Savant, Marilyn (17. února 1991a). „Zeptej se Marilyn“ . Průvod : 12. Archivováno od originálu dne 21. ledna 2013 . Vyvolány 12 November 2012 .
- vos Savant, Marilyn (listopad 1991c). „Odpověď Marilyn vos Savantové“. Dopisy editorovi. Americký statistik . 45 (4): 347.
- vos Savant, Marilyn (1996). Síla logického myšlení . Svatomartinský tisk. p. 5 . ISBN 0-312-15627-8.
- Williams, Richard (2004). „Dodatek D: Kontroverze Monty Hall“ (PDF) . Poznámky kursu pro Sociology Graduate statistika I . Citováno 2008-04-25 .
- Whitaker, Craig F. (9. září 1990). "[Formulace od Marilyn vos Savant of Question položená v dopise od Craiga Whitakera]. Zeptejte se Marilyn". Průvod : 16.
Další čtení
- Gill, Richard (2011b). „Problém Monty Hall (verze 5)“ . StatProb: Encyklopedie sponzorovaná statistickými a pravděpodobnostními společnostmi . Archivováno od originálu dne 2016-01-21 . Citováno 2011-04-03 .
- vos Savant, Marilyn (7. července 1991b). „Zeptej se Marilyn“ . Průvod : 26. Archivováno od originálu dne 21. ledna 2013 . Vyvolány 12 November 2012 .
- vos Savant, Marilyn (26. listopadu 2006). „Zeptej se Marilyn“. Průvod : 6.
externí odkazy
- The Game Show Problem - původní otázka a odpovědi na webových stránkách Marilyn vos Savant
- Kalifornská univerzita v San Diegu, Monty zná verzi a Monty nezná verzi, vysvětlení hry
- Monty Hall v Curlie
- „Stick or switch? Probability and the Monty Hall problem“ , BBC News Magazine , 11. září 2013 (video). Matematik Marcus du Sautoy vysvětluje paradox Monty Hall.