V dynamiky tekutin , stagnace bod toku představuje tok tekutiny v bezprostřední blízkosti pevného povrchu. Jak se kapalina přibližuje k povrchu, rozdělí se na dva proudy. Ačkoli tekutina stagnuje všude na pevném povrchu kvůli neklouzavému stavu , název stagnační bod odkazuje na stagnační body inviscidních Eulerových řešení.
Hiemenzův tok
Dvojrozměrný tok stagnačních bodů
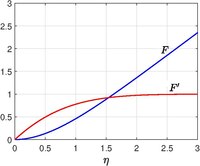
Hiemenz formuloval problém a řešení vypočítal numericky v roce 1911 a následně Leslie Howarth (1934). Tok v okolí bodu stagnace lze modelovat tokem směrem k nekonečné ploché desce, i když celé tělo je zakřivené (lokální zakřivení je zanedbatelné). Nechte desku být v rovině, která představuje bod stagnace. Funkce a rychlost neviditelného proudu z teorie potenciálního toku jsou





kde je libovolná konstanta (představuje rychlost deformace v nastavení protiproudu). Pro skutečnou tekutinu (včetně viskózních efektů) existuje podobné řešení, pokud je definováno


kde je kinematická viskozita a je tloušťka mezní vrstvy, ale je konstantní (vířivost generovaná na pevném povrchu je zabráněna difúzi daleko protilehlou konvekcí, podobné profily jsou mezní vrstva Blasius s odsáváním, von Kármánův vířící tok atd.), Potom se složky rychlosti a následně tlak a rovnice pro použití Navier-Stokesových rovnic jsou





a okrajová podmínka kvůli žádnému průniku a neklouzavosti a podmínka volného proudu pro (Poznámka: okrajové podmínky pro daleko od desky nejsou specifikovány, protože jsou součástí řešení - typický problém mezní vrstvy) jsou



Zde formulovaným problémem je speciální případ mezní vrstvy Falkner-Skan . Asymptotické formy pro velké jsou


kde je tloušťka posunutí .

Tok stagnačního bodu s překládací deskou
Tok modelu stagnačního bodu s pohyblivou deskou s konstantní rychlostí lze považovat za model pro rotaci pevných látek v blízkosti bodů stagnace. Funkce streamu je


kde splňuje rovnici


a Rott (1956) poskytli řešení jako 
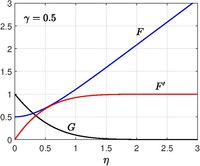
Šikmý tok stagnačního bodu
Předchozí analýzy předpokládají, že tok naráží do normálního směru. Funkce inviscid stream pro tok šikmého bodu stagnace se získá přidáním konstantní vířivosti .


Odpovídající analýzu viskózní tekutiny studují Stuart (1959), Tamada (1979) a Dorrepaal (1986). Funkce podobného streamu je,

kde splňuje rovnici

-
 .
.
Homannův tok
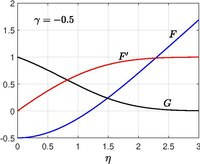
Homannův tok se vstřikováním
Odpovídající problém v osově souměrné souřadnici řeší Homann (1936) a slouží jako model pro proudění kolem bodu stagnace koule. Paul A. Libby (1974) (1976) uvažoval o Homannově proudění s neustále se pohybující deskou s rychlostí a také umožňoval sání / vstřikování s rychlostí na povrchu.


Self-podobné řešení se získá zavedením následující transformace pro rychlost ve válcových souřadnicích


a tlak je dán

Proto se rovnice Navier-Stokes redukují na

s okrajovými podmínkami,

Když je klasický Homannův problém vyřešen.

Rovinné protiproudy
Trysky vycházející z automatů vytvářejí mezi teorií potenciálu stagnační bod. Tok poblíž bodu stagnace lze studovat pomocí podobného řešení. Toto nastavení je široce používáno v experimentech spalování . Počáteční studie dopadu stagnačních toků je způsobena CY Wangem. Nechte dvě tekutiny s konstantními vlastnostmi označenými příponou, která teče z opačného směru, a předpokládejme, že obě tekutiny jsou nemísitelné a rozhraní (umístěné v ) je rovinné. Rychlost je dána vztahem



kde jsou rychlosti deformace tekutin. Na rozhraní musí být rychlosti, tangenciální napětí a tlak spojité. Představujeme podobnou transformaci,



výsledkové rovnice,


Stane se stav bez penetrace na rozhraní a stav volného toku daleko od stagnační roviny

Rovnice však vyžadují další dvě okrajové podmínky. Na , tangenciální rychlosti , tangenciální napětí a tlak jsou spojité. Proto,





kde (z vnějšího problému inviscid) se používá. Oba nejsou apriori známé , ale jsou odvozeny z odpovídajících podmínek. Třetí rovnice je určení změny vnějšího tlaku v důsledku vlivu viskozity. Existují tedy pouze dva parametry, kterými se řídí tok




pak se stanou okrajové podmínky
-
 .
.
Konstantní hustota a konstantní viskozita
Když jsou hustoty a viskozity dvou nárazových trysek stejné a konstantní, pak je také deformační rychlost konstantní a řešení potenciálního toku se stane řešením Navier-Stokesových rovnic, tj.


všude v doméně toku. Kerr a Dold našli v roce 1994 další nové řešení zvané jako Kerr – Doldův vír Navierových-Stokesových rovnic v podobě periodického pole ustálených vírů superponovaných na protiproudé proudy s konstantní hustotou a konstantní viskozitou.
Reference