Úhel rovnoběžnosti - Angle of parallelism

Pokud je úhel B pravý a Aa a Bb jsou omezující rovnoběžně, pak úhel mezi Aa a AB je úhel rovnoběžnosti.

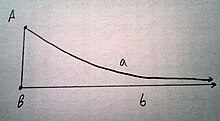
V hyperbolické geometrii je úhel rovnoběžnosti , je úhel v jednom vrcholu pravého hyperbolického trojúhelníku , který má dva asymptotické rovnoběžné strany. Úhel závisí na délce segmentu a mezi pravým úhlem a vrcholem úhlu rovnoběžnosti. ${\ displaystyle \ Pi (a)}$

Vzhledem k bodu mimo přímku, pokud shodíme kolmici na přímku z bodu, pak a je vzdálenost podél tohoto kolmého segmentu a φ nebo je nejmenší úhel, takže přímka tažená bodem v tomto úhlu není protínají danou čáru. Protože dvě strany jsou asymptotické paralelní, ${\ displaystyle \ Pi (a)}$

${\ displaystyle \ lim _ {a \ to 0} \ Pi (a) = {\ tfrac {1} {2}} \ pi \ quad {\ text {a}} \ quad \ lim _ {a \ to \ infty } \ Pi (a) = 0.}$

Existuje pět ekvivalentní výrazy, které se týkají i : ${\ displaystyle \ Pi (a)}$

${\ displaystyle \ sin \ Pi (a) = \ operatorname {sech} a = {\ frac {1} {\ cosh a}} = {\ frac {2} {e ^ {a} + e ^ {- a} }} \,}$

${\ displaystyle \ cos \ Pi (a) = \ tanh a = {\ frac {e ^ {a} -e ^ {- a}} {e ^ {a} + e ^ {- a}}} \,}$

${\ displaystyle \ tan \ Pi (a) = \ operatorname {csch} a = {\ frac {1} {\ sinh a}} = {\ frac {2} {e ^ {a} -e ^ {- a} }} \,}$

${\ displaystyle \ tan \ left ({\ tfrac {1} {2}} \ Pi (a) \ right) = e ^ {- a},}$

${\ displaystyle \ Pi (a) = {\ tfrac {1} {2}} \ pi - \ operatorname {gd} (a),}$

kde sinh, cosh, tanh, sech a csch jsou hyperbolické funkce a gd je gudermannská funkce .

Konstrukce

János Bolyai objevil konstrukci, která dává asymptotické rovnoběžky s k přímce r procházející bodem A ne na r . Umístěte kolmici z A na B na r . Vybrat jakýkoliv bod C o r odlišný od B . Postavit kolmo t k r u C . Umístěte kolmici z A na D na t . Pak délka DA je delší než banky , ale kratší než CA . Nakreslete kruh kolem C s poloměrem rovným DA . To bude protínat segment AB v bodě E . Poté je úhel BEC nezávislý na délce BC , pouze v závislosti na AB ; je to úhel paralelismu. Zkonstruujte s skrz A v úhlu BEC od AB .

${\ displaystyle \ sin BEC = {\ frac {\ sinh {BC}} {\ sinh {CE}}} = {\ frac {\ sinh {BC}} {\ sinh {DA}}} = {\ frac {\ sinh {BC}} {\ sin {ACD} \ sinh {CA}}} = {\ frac {\ sinh {BC}} {\ cos {ACB} \ sinh {CA}}} = {\ frac {\ sinh { BC} \ tanh {CA}} {\ tanh {CB} \ sinh {CA}}} = {\ frac {\ cosh {BC}} {\ cosh {CA}}} = {\ frac {\ cosh {BC} } {\ cosh {CB} \ cosh {AB}}} = {\ frac {1} {\ cosh {AB}}} \ ,.}$

Zde použité vzorce viz Trigonometrie pravoúhlých trojúhelníků .

Dějiny

Úhel paralelismu byl vyvinut v roce 1840 v německém publikaci „Geometrische Untersuchungen zur teorie der Parallellinien“ od Nikolaje Lobachevsky .

Tato publikace se stala v angličtině široce známou poté, co texaský profesor GB Halsted v roce 1891 vytvořil překlad. ( Geometrické výzkumy teorie rovnoběžek )

Následující pasáže definují tento stěžejní koncept v hyperbolické geometrii:

Úhel HAD mezi rovnoběžkou HA a kolmým AD se nazývá paralelní úhel (úhel rovnoběžnosti), který zde označíme Π (p) pro AD = p .

Demonstrace

Úhel rovnoběžnosti, φ , formulovaný jako: (a) Úhel mezi osou x a přímkou ​​probíhající od x , středu Q , k y , průsečíku Q, a (b) Úhel od tečna Q na y k ose y.
Tento diagram se žlutým ideálním trojúhelníkem je podobný tomu, který se nachází v knize Smogorzhevského.

V Poincarém polorovinovém modelu hyperbolické roviny (viz Hyperbolické pohyby ) lze určit vztah φ k a s euklidovskou geometrií . Nechť Q je půlkruh s průměrem na ose x, který prochází body (1,0) a (0, y ), kde y > 1. Protože Q je tečna k jednotkovému půlkruhu se středem v počátku, dva půlkruhy představují paralelní hyperbolické čáry . Y aretačním kroužkem kříže oba půlkruhy, takže pravý úhel s jednotkovou půlkruhu a variabilní úhel cp s Q . Úhel ve středu Q podřízený poloměrem k (0,  y ) je také φ, protože dva úhly mají strany, které jsou kolmé, levá strana k levé straně a pravá strana k pravé straně. Půlkruh Q má střed na ( x , 0), x <0, takže jeho poloměr je 1 -  x . Poloměr Q na druhou je tedy

${\ displaystyle x ^ {2} + y ^ {2} = (1-x) ^ {2},}$

proto

${\ displaystyle x = {\ tfrac {1} {2}} (1-y ^ {2}).}$

Metrika na Poincaré polorovině modelu z hyperbolické geometrii parametrizes vzdálenost na paprsku {(0,  y ): y > 0} s logaritmické opatření . Nechť log  y = a , takže y = e ^a, kde e je základem přirozeného logaritmu . Potom lze vztah mezi φ a a odvodit z trojúhelníku {( x , 0), (0, 0), (0,  y )}, například:

${\ displaystyle \ tan \ phi = {\ frac {y} {- x}} = {\ frac {2y} {y ^ {2} -1}} = {\ frac {2e ^ {a}} {e ^ {2a} -1}} = {\ frac {1} {\ sinh a}}.}$

Reference

• Marvin J. Greenberg (1974) Euclidean and Non-Euclidean Geometries , str. 211–3, WH Freeman & Company .
• Robin Hartshorne (1997) Companion to Euclid pp. 319, 325, American Mathematical Society , ISBN  0821807978 .
• Jeremy Gray (1989) Ideas of Space: Euclidean, Non-Euclidean, and Relativistic , 2. vydání, Clarendon Press , Oxford (viz strany 113 až 118).
• Béla Kerékjártó (1966) Les Fondements de la Géométry , Tome Deux, § 97,6 Angle de parallélisme de la géométry hyperbolique, str. 411,2, Akademiai Kiado, Budapešť.