Analýza nezávislých komponent - Independent component analysis

Část série na
Strojové učení a dolování dat
Problémy Klasifikace Shlukování Regrese Detekce anomálií Čištění dat AutoML Pravidla asociace Posílení učení Strukturovaná predikce Funkce inženýrství Funkce učení Online učení Učení pod dohledem Učení bez dozoru Naučit se řadit Gramatická indukce
Učení pod dohledem ( klasifikace  • regrese ) Rozhodovací stromy Soubory Pytlování Posílení Náhodný les k -NN Lineární regrese Naivní Bayes Umělé neuronové sítě Logistická regrese Perceptron Relevantní vektorový stroj (RVM) Podpora vektorového stroje (SVM)
Shlukování BŘÍZA LÉK Hierarchický k -znamená Očekávání – maximalizace (EM) DBSCAN OPTIKA Střední posun
Redukce rozměrů Faktorová analýza CCA ICA LDA NMF PCA PGD t-SNE
Strukturovaná predikce Grafické modely Bayesova síť Podmíněné náhodné pole Skrytý Markov
Detekce anomálií k -NN Faktor místní odlehlosti
Umělá neurální síť Autoencoder Kognitivní výpočetní technika Hluboké učení DeepDream Vícevrstvý perceptron RNN LSTM GRU ESN Omezený stroj Boltzmann GAN SOM Konvoluční neurální síť U-Net Transformátor Rozšíření neuronové sítě Memtranzistor Elektrochemická RAM (ECRAM)
Posílení učení Q-učení SARSA Časový rozdíl (TD)
Teorie Kompromis předpojatosti a rozptylu Teorie výpočetního učení Empirická minimalizace rizik Occam učení Učení PAC Statistické učení VC teorie
Místa strojového učení NeurIPS ICML ML JMLR ArXiv: cs.LG
Související články Glosář umělé inteligence Seznam datových sad pro výzkum strojového učení Nástin strojového učení
proti t E

Při zpracování signálu je nezávislá analýza komponent ( ICA ) výpočetní metodou pro oddělení vícerozměrného signálu na aditivní subkomponenty. To se provádí za předpokladu, že subkomponenty jsou potenciálně ne-gaussovské signály a že jsou na sobě statisticky nezávislé . ICA je speciální případ oddělení slepých zdrojů . Běžným příkladem aplikace je „ problém koktejlové párty “ naslouchání řeči jedné osoby v hlučné místnosti.

Úvod

Přehrávejte média

ICA na čtyři náhodně smíšená videa. Nahoru: Původní zdrojová videa. Uprostřed: Čtyři náhodné směsi použité jako vstup do algoritmu. Dole: Rekonstruovaná videa.

Analýza nezávislých komponent se pokouší rozložit vícerozměrný signál na nezávislé ne-gaussovské signály. Jako příklad, zvuk je obvykle signál, který se skládá z numerického sčítání signálů z několika zdrojů vždy, t. Otázkou pak je, zda je možné tyto přispívající zdroje oddělit od pozorovaného celkového signálu. Když je předpoklad statistické nezávislosti správný, slepé oddělení ICA smíšeného signálu poskytuje velmi dobré výsledky. Používá se také pro signály, které by neměly být generovány smícháním pro účely analýzy.

Jednoduchou aplikací ICA je „ problém koktejlové párty “, kde jsou základní řečové signály odděleny od ukázkových dat, která se skládají z lidí, kteří současně mluví v místnosti. Obvykle je problém zjednodušen tím, že se nepředpokládá žádné časové zpoždění nebo ozvěna. Všimněte si, že filtrovaný a zpožděný signál je kopií závislé komponenty, a proto není porušen předpoklad statistické nezávislosti.

Míchací závaží pro konstrukci pozorovaných signálů ze složek lze umístit do matice. Důležitá věc, kterou je třeba vzít v úvahu, je, že pokud jsou přítomny zdroje, jsou k obnovení původních signálů zapotřebí alespoň pozorování (např. Mikrofony, pokud je pozorovaný signál zvukový). Když existuje stejný počet pozorování a zdrojových signálů, je směšovací matice čtvercová ( ). Byly vyšetřovány i další případy poddeterminovaného ( ) a předurčeného ( ). ${\ textstyle M}$${\ textstyle N}$${\ textstyle M \ times N}$${\ textstyle N}$${\ textstyle N}$${\ textstyle M = N}$${\ textstyle M <N}$${\ textstyle M> N}$

Že ICA separace smíšených signálů poskytuje velmi dobré výsledky, je založeno na dvou předpokladech a třech efektech míchání zdrojových signálů. Dva předpoklady:

1. Zdrojové signály jsou na sobě nezávislé.
2. Hodnoty v každém zdrojovém signálu mají negaussovské rozdělení.

Tři efekty míchání zdrojových signálů:

1. Nezávislost: Podle předpokladu 1 jsou zdrojové signály nezávislé; jejich signální směsi však nejsou. Důvodem je, že směsi signálů sdílejí stejné zdrojové signály.
2. Normalita: Podle věty o centrálním limitu směřuje rozdělení součtu nezávislých náhodných proměnných s konečným rozptylem ke gaussovskému rozdělení.
   Volně řečeno, součet dvou nezávislých náhodných proměnných má obvykle distribuci, která je bližší Gaussovu než kterákoli ze dvou původních proměnných. Zde považujeme hodnotu každého signálu za náhodnou proměnnou.
3. Složitost: Časová složitost jakékoli signální směsi je větší než u nejjednoduššího zdrojového signálu zdroje.

Tyto zásady přispívají k základnímu zřízení ICA. Pokud jsou signály extrahované ze sady směsí nezávislé a mají ne-gaussovské histogramy nebo mají nízkou složitost, pak musí jít o zdrojové signály.

Definování nezávislosti komponent

ICA vyhledává nezávislé složky (nazývané také faktory, latentní proměnné nebo zdroje) maximalizací statistické nezávislosti odhadovaných složek. Můžeme si vybrat jeden z mnoha způsobů, jak definovat proxy pro nezávislost, a tato volba určuje formu algoritmu ICA. Dvě nejširší definice nezávislosti pro ICA jsou

1. Minimalizace vzájemných informací
2. Maximalizace ne-gaussiánství

Rodina IMI algoritmů Minimalizace vzájemných informací (MMI) používá opatření jako Kullback-Leibler Divergence a maximální entropie . Non-Gaussianity rodina ICA algoritmů, motivovaná centrální limitní větou , používá kurtózu a negentropii .

Typické algoritmy pro ICA používají jako kroky předzpracování centrování (odečtení průměru k vytvoření signálu nulového průměru), bělení (obvykle s rozkladem vlastních čísel ) a redukci rozměrů za účelem zjednodušení a snížení složitosti problému pro skutečný iterační algoritmus. Bělení a redukci rozměrů lze dosáhnout analýzou hlavních složek nebo rozkladem singulárních hodnot . Bělení zajišťuje, že se všemi dimenzemi je před spuštěním algoritmu a priori zacházeno stejně . Mezi dobře známé algoritmy pro ICA patří mimo jiné infomax , FastICA , JADE a analýza komponent nezávislá na jádře . Obecně ICA nedokáže identifikovat skutečný počet zdrojových signálů, jednoznačně správné uspořádání zdrojových signálů ani správné škálování (včetně znaménka) zdrojových signálů.

ICA je důležitá pro oddělení slepých signálů a má mnoho praktických aplikací. Úzce to souvisí (nebo dokonce ve zvláštním případě) s hledáním faktoriálního kódu dat, tj. S novou vektorovou reprezentací každého datového vektoru tak, že je výsledným kódovým vektorem jednoznačně zakódován (beze ztrát) kódování), ale složky kódu jsou statisticky nezávislé.

Matematické definice

Lineární nezávislou komponentní analýzu lze rozdělit na bezhlučné a hlučné případy, kde bezhlučná ICA je zvláštní případ hlučné ICA. Nelineární ICA by měla být považována za samostatný případ.

Obecná definice

Data jsou reprezentována pozorovaným náhodným vektorem a skrytými komponentami jako náhodný vektor . Úkolem je transformovat pozorovaná data pomocí lineární statické transformace jako do vektoru maximálně nezávislých komponent měřených nějakou funkcí nezávislosti. ${\ displaystyle {\ boldsymbol {x}} = (x_ {1}, \ ldots, x_ {m})^{T}}$${\ displaystyle {\ boldsymbol {s}} = (s_ {1}, \ ldots, s_ {n})^{T}.}$${\ displaystyle {\ boldsymbol {x}},}$${\ displaystyle {\ boldsymbol {W}}}$${\ displaystyle {\ boldsymbol {s}} = {\ boldsymbol {W}} {\ boldsymbol {x}},}$${\ displaystyle {\ boldsymbol {s}}}$${\ Displaystyle F (s_ {1}, \ ldots, s_ {n})}$

Generativní model

Lineární bezhlučný ICA

Složky pozorovaného náhodného vektoru jsou generovány jako součet nezávislých komponent , : ${\ displaystyle x_ {i}}$${\ displaystyle {\ boldsymbol {x}} = (x_ {1}, \ ldots, x_ {m})^{T}}$${\ displaystyle s_ {k}}$${\ Displaystyle k = 1, \ ldots, n}$

${\ Displaystyle x_ {i} = a_ {i, 1} s_ {1} +\ cdots +a_ {i, k} s_ {k} +\ cdots +a_ {i, n} s_ {n}}$

vážené směšovacími závažími . ${\ displaystyle a_ {i, k}}$

Stejný generativní model lze zapsat ve vektorové podobě jako tam, kde pozorovaný náhodný vektor je reprezentován základními vektory . Základní vektory tvoří sloupce směšovací matice a generativní vzorec lze zapsat jako , kde . ${\ displaystyle {\ boldsymbol {x}} = \ sum _ {k = 1}^{n} s_ {k} {\ boldsymbol {a}} _ {k}}$${\ displaystyle {\ boldsymbol {x}}}$${\ displaystyle {\ boldsymbol {a}} _ {k} = ({\ boldsymbol {a}} _ {1, k}, \ ldots, {\ boldsymbol {a}} _ {m, k})^{T }}$${\ displaystyle {\ boldsymbol {a}} _ {k}}$${\ displaystyle {\ boldsymbol {A}} = ({\ boldsymbol {a}} _ {1}, \ ldots, {\ boldsymbol {a}} _ {n})}$${\ displaystyle {\ boldsymbol {x}} = {\ boldsymbol {A}} {\ boldsymbol {s}}}$${\ displaystyle {\ boldsymbol {s}} = (s_ {1}, \ ldots, s_ {n})^{T}}$

Vzhledem k modelu a realizacím (vzorkům) náhodného vektoru je úkolem odhadnout jak směšovací matici, tak zdroje . To se provádí adaptivním výpočtem vektorů a nastavením nákladové funkce, která buď maximalizuje negaussianitu vypočítaných, nebo minimalizuje vzájemné informace. V některých případech lze v nákladové funkci použít apriorní znalost rozdělení pravděpodobnosti zdrojů. ${\ displaystyle {\ boldsymbol {x}} _ {1}, \ ldots, {\ boldsymbol {x}} _ {N}}$${\ displaystyle {\ boldsymbol {x}}}$${\ displaystyle {\ boldsymbol {A}}}$${\ displaystyle {\ boldsymbol {s}}}$${\ displaystyle {\ boldsymbol {w}}}$${\ displaystyle s_ {k} = {\ boldsymbol {w}}^{T} {\ boldsymbol {x}}}$

Původní zdroje lze získat vynásobením pozorovaných signálů inverzní směšovací maticí , známou také jako nesmísící matice. Zde se předpokládá, že směšovací matice je square ( ). Je -li počet základních vektorů větší než rozměrnost pozorovaných vektorů , je úkol nadbytečný, ale je stále řešitelný pseudo inverzní . ${\ displaystyle {\ boldsymbol {s}}}$${\ displaystyle {\ boldsymbol {x}}}$${\ displaystyle {\ boldsymbol {W}} = {\ boldsymbol {A}}^{-1}}$${\ Displaystyle n = m}$${\ Displaystyle n> m}$

Lineární hlučný ICA

S přidaným předpokladem nulového průměru a nekorelovaného gaussovského šumu má formu ICA model . ${\ displaystyle n \ sim N (0, \ operatorname {diag} (\ Sigma))}$${\ displaystyle {\ boldsymbol {x}} = {\ boldsymbol {A}} {\ boldsymbol {s}}+n}$

Nelineární ICA

Míchání zdrojů nemusí být lineární. Použitím nelineární směšovací funkce s parametry je nelineární ICA model . ${\ Displaystyle f (\ cdot | \ theta)}$${\ displaystyle \ theta}$${\ Displaystyle x = f (s | \ theta)+n}$

Identifikovatelnost

Nezávislé komponenty jsou identifikovatelné až do permutace a škálování zdrojů. Tato identifikace vyžaduje, aby:

• Maximálně jeden ze zdrojů je Gaussian,${\ displaystyle s_ {k}}$
• Počet pozorovaných směsí, musí být alespoň tak velké, jako je počet odhadovaných složek : . Je ekvivalentní říci, že směšovací matice musí mít plnou pozici, aby mohla existovat její inverze.${\ displaystyle m}$${\ displaystyle n}$${\ Displaystyle m \ geq n}$${\ displaystyle {\ boldsymbol {A}}}$

Binární ICA

Zvláštní variantou ICA je binární ICA, ve které jsou zdroje signálu i monitory v binární formě a pozorování z monitorů jsou disjunktivní směsi binárních nezávislých zdrojů. Ukázalo se, že problém má aplikace v mnoha doménách, včetně lékařské diagnostiky , přiřazení více klastrů , síťové tomografie a správy internetových zdrojů .

Nechť je množina binárních proměnných z monitorů a je množina binárních proměnných ze zdrojů. Propojení zdroje a monitoru je reprezentováno (neznámou) směšovací maticí , kde označuje, že signál z i -tého zdroje může být pozorován j -tým monitorem. Systém funguje následovně: kdykoli je zdroj aktivní ( ) a je připojen k monitoru ( ), monitor bude sledovat určitou aktivitu ( ). Formálně máme: ${\ displaystyle {x_ {1}, x_ {2}, \ ldots, x_ {m}}}$${\ displaystyle m}$${\ displaystyle {y_ {1}, y_ {2}, \ ldots, y_ {n}}}$${\ displaystyle n}$${\ textstyle {\ boldsymbol {G}}}$${\ displaystyle g_ {ij} = 1}$${\ displaystyle i}$${\ displaystyle y_ {i} = 1}$${\ displaystyle j}$${\ displaystyle g_ {ij} = 1}$${\ displaystyle j}$${\ displaystyle x_ {j} = 1}$

${\ Displaystyle x_ {i} = \ bigvee _ {j = 1}^{n} (g_ {ij} \ wedge y_ {j}), i = 1,2, \ ldots, m,}$

kde je booleovský AND a je booleovský NEBO. Hluk není explicitně modelován, lze jej naopak považovat za nezávislé zdroje. ${\ displaystyle \ wedge}$${\ displaystyle \ vee}$

Výše uvedený problém lze heuristicky vyřešit za předpokladu, že proměnné jsou spojité a běží FastICA na binárních pozorovacích datech, aby se získala směšovací matice (reálné hodnoty), a poté aplikujte techniky kulatého čísla na získání binárních hodnot. Ukázalo se, že tento přístup přináší vysoce nepřesné výsledky. ${\ textstyle {\ boldsymbol {G}}}$${\ textstyle {\ boldsymbol {G}}}$

Další metodou je použít dynamické programování : rekurzivně rozbít pozorovací matici na její submatice a spustit na těchto dílčích maticích inferenční algoritmus. Pozorování klíč, který vede k tomuto algoritmu je sub-matice z kterých odpovídá nezaujatého pozorování matrice skrytých složek, které nemají připojení k tého monitoru. Experimentální výsledky ukazují, že tento přístup je přesný při mírných hladinách hluku. ${\ textstyle {\ boldsymbol {X}}}$${\ textstyle {\ boldsymbol {X}}^{0}}$${\ textstyle {\ boldsymbol {X}}}$${\ textstyle x_ {ij} = 0, \ forall j}$${\ displaystyle i}$

Rámec Generalized Binary ICA zavádí širší formulaci problému, která nevyžaduje žádné znalosti o generativním modelu. Jinými slovy, tato metoda se pokouší rozložit zdroj na jeho nezávislé komponenty (co nejvíce a bez ztráty jakýchkoli informací) bez předchozího předpokladu o způsobu jeho generování. Ačkoli se tento problém jeví jako poměrně složitý, lze jej přesně vyřešit pomocí algoritmu stromu větví a vázaných vyhledávacích stromů nebo těsně horní hranice pomocí jediného násobení matice vektorem.

Metody separace slepých zdrojů

Pronásledování projekce

Směsi signálů mívají funkce Gaussovy hustoty pravděpodobnosti a zdrojové signály mívají funkce jiné než Gaussovy hustoty pravděpodobnosti. Každý zdrojový signál lze extrahovat ze sady směsí signálů odebráním vnitřního produktu hmotnostního vektoru a těch signálních směsí, kde tento vnitřní produkt poskytuje ortogonální projekci směsí signálů. Zbývající výzvou je nalezení takového hmotnostního vektoru. Jedním z typů metod, jak toho dosáhnout, je pronásledování .

Pronásledování projekce hledá jednu projekci najednou tak, aby extrahovaný signál byl pokud možno ne-gaussovský. To je v kontrastu s ICA, která obvykle extrahuje signály M současně ze směsí signálů M , což vyžaduje odhad M × M unmixující matice. Jednou praktickou výhodou sledování projekce oproti ICA je, že lze v případě potřeby extrahovat méně než M signálů, kde je každý zdrojový signál extrahován ze směsí M signálů pomocí hmotnostního vektoru M -prvku.

Můžeme použít kurtózu k obnovení signálu z více zdrojů nalezením správných vektorů hmotnosti s využitím pronásledování.

Kurtóza funkce hustoty pravděpodobnosti signálu pro konečný vzorek se vypočítá jako

${\ Displaystyle K = {\ frac {\ operatorname {E} [(\ mathbf {y} -\ mathbf {\ overline {y}})^{4}]} {(\ operatorname {E} [(\ mathbf { y} -\ mathbf {\ overline {y}})^{2}])^{2}}} -3}$

kde je vzorek průměr z , extrahovaných signálů. Konstanta 3 zajišťuje, že gaussovské signály mají nulovou špičatost, super-gaussovské signály mají pozitivní kurtózu a sub-gaussovské signály negativní špičatost. Jmenovatel je rozptyl o , a zajišťuje, že měřená špičatosti bere v úvahu signál rozptylu. Cílem pronásledování je maximalizovat kurtózu a extrahovat signál tak, aby byl co nejnormálnější. ${\ displaystyle \ mathbf {\ overline {y}}}$${\ displaystyle \ mathbf {y}}$${\ displaystyle \ mathbf {y}}$

Pomocí kurtózy jako měřítka nenormality můžeme nyní zkoumat, jak se kurtóza signálu extrahovaného ze sady M směsí mění, když se vektor hmotnosti otáčí kolem počátku. Vzhledem k našemu předpokladu, že každý zdrojový signál je super-gaussovský, očekávali bychom: ${\ Displaystyle \ mathbf {y} = \ mathbf {w} ^{T} \ mathbf {x}}$${\ Displaystyle \ mathbf {x} = (x_ {1}, x_ {2}, \ ldots, x_ {M})^{T}}$${\ displaystyle \ mathbf {w}}$${\ displaystyle \ mathbf {s}}$

1. kurtóza extrahovaného signálu bude maximální přesně kdy .${\ displaystyle \ mathbf {y}}$${\ Displaystyle \ mathbf {y} = \ mathbf {s}}$
2. kurtóza extrahovaného signálu bude maximální, když je kolmá k projektovaným osám, nebo protože víme, že optimální vektor hmotnosti by měl být ortogonální k transformované ose nebo .${\ displaystyle \ mathbf {y}}$${\ displaystyle \ mathbf {w}}$${\ displaystyle S_ {1}}$${\ displaystyle S_ {2}}$${\ displaystyle S_ {1}}$${\ displaystyle S_ {2}}$

U signálů více zdrojových směsí můžeme k obnovení signálů použít kurtózu a Gram-Schmidtovu ortogonalizaci (GSO). Vzhledem ke směsi signálů M v M- dimenzionálním prostoru GSO promítá tyto datové body do ( M-1 ) -dimenzionálního prostoru pomocí vektoru hmotnosti. Nezávislost extrahovaných signálů můžeme zaručit pomocí GSO.

Abychom našli správnou hodnotu , můžeme použít metodu gradientového klesání . Data nejprve vybělíme a přeměníme na novou směs , která má jednotkový rozptyl, a . Tento proces lze dosáhnout aplikací rozkladu singulárních hodnot na , ${\ displaystyle \ mathbf {w}}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {z}}$${\ Displaystyle \ mathbf {z} = (z_ {1}, z_ {2}, \ ldots, z_ {M})^{T}}$${\ displaystyle \ mathbf {x}}$

${\ Displaystyle \ mathbf {x} = \ mathbf {U} \ mathbf {D} \ mathbf {V} ^{T}}$

Přeškálování každého vektoru , a nechte . Signál extrahovaný váženým vektorem je . Pokud má hmotnostní vektor w jednotkovou délku, pak rozptyl y je také 1, tj . Kurtózu lze tedy zapsat jako: ${\ displaystyle U_ {i} = U_ {i}/\ operatorname {E} (U_ {i}^{2})}$${\ displaystyle \ mathbf {z} = \ mathbf {U}}$${\ displaystyle \ mathbf {w}}$${\ Displaystyle \ mathbf {y} = \ mathbf {w} ^{T} \ mathbf {z}}$${\ displaystyle \ operatorname {E} [(\ mathbf {w} ^{T} \ mathbf {z}) ^{2}] = 1}$

${\ displaystyle K = {\ frac {\ operatorname {E} [\ mathbf {y} ^{4}]} {(\ operatorname {E} [\ mathbf {y} ^{2}]) ^{2}} } -3 = \ jméno operátora {E} [(\ mathbf {w} ^{T} \ mathbf {z}) ^{4}]-3.}$

Proces aktualizace pro : ${\ displaystyle \ mathbf {w}}$

${\ Displaystyle \ mathbf {w} _ {new} = \ mathbf {w} _ {old}-\ eta \ operatorname {E} [\ mathbf {z} (\ mathbf {w} _ {old}^{T} \ mathbf {z})^{3}].}$

kde je malá konstanta, která zaručuje, že konverguje k optimálnímu řešení. Po každé aktualizaci normalizujeme , nastavíme a opakujeme proces aktualizace až do konvergence. K aktualizaci vektoru hmotnosti můžeme také použít jiný algoritmus . ${\ displaystyle \ eta}$${\ displaystyle \ mathbf {w}}$${\ displaystyle \ mathbf {w} _ {new} = {\ frac {\ mathbf {w} _ {new}} {| \ mathbf {w} _ {new} |}}}}$${\ displaystyle \ mathbf {w} _ {old} = \ mathbf {w} _ {new}}$${\ displaystyle \ mathbf {w}}$

Dalším přístupem je použití negentropie místo kurtózy. Použití negentropie je robustnější metodou než kurtóza, protože kurtóza je velmi citlivá na odlehlé hodnoty. Metody negentropie jsou založeny na důležité vlastnosti Gaussova rozdělení: Gaussova proměnná má největší entropii ze všech spojitých náhodných proměnných se stejným rozptylem. To je také důvod, proč chceme najít nejvíce nongauských proměnných. Jednoduchý důkaz najdete v Diferenciální entropii .

${\ Displaystyle J (x) = S (y) -S (x) \,}$

y je Gaussova náhodná proměnná stejné kovarianční matice jako x

${\ Displaystyle S (x) =-\ int p_ {x} (u) \ log p_ {x} (u) du}$

Aproximace negentropie je

${\ Displaystyle J (x) = {\ frac {1} {12}} (E (x^{3}))^{2}+{\ frac {1} {48}} (kurt (x))^ {2}}$

Důkaz lze nalézt v původních Comonových listech; byla reprodukována v knize Independent Component Analysis od Aapo Hyvärinen, Juha Karhunen a Erkki Oja. Tato aproximace také trpí stejným problémem jako kurtóza (citlivost na odlehlé hodnoty). Byly vyvinuty další přístupy.

${\ Displaystyle J (y) = k_ {1} (E (G_ {1} (y)))^{2}+k_ {2} (E (G_ {2} (y))-E (G_ {2 } (v))^{2}}$

Na výběr a jsou ${\ displaystyle G_ {1}}$${\ displaystyle G_ {2}}$

${\ displaystyle G_ {1} = {\ frac {1} {a_ {1}}} \ log (\ cosh (a_ {1} u))}$ a ${\ displaystyle G_ {2} =-\ exp (-{\ frac {u^{2}} {2}})}$

Na základě infomaxu

Infomax ICA je v podstatě vícerozměrná, paralelní verze sledování projekce. Zatímco sledování projekce extrahuje sérii signálů jeden po druhém ze sady M signálních směsí, ICA extrahuje M signály paralelně. Díky tomu je ICA odolnější než projekce.

Metoda pronásledování využívá ortogonalizaci Gram-Schmidt k zajištění nezávislosti extrahovaného signálu, zatímco ICA používá infomax a odhad maximální pravděpodobnosti k zajištění nezávislosti extrahovaného signálu. Nestandardnosti extrahovaného signálu je dosaženo přiřazením příslušného modelu nebo předchozího signálu.

Stručně řečeno, proces ICA založený na infomaxu je: vzhledem k sadě směsí signálů a sadě identických nezávislých modelových kumulativních distribučních funkcí (cdfs) hledáme unmixovací matici, která maximalizuje společnou entropii signálů , kde jsou signály extrahovány od . Vzhledem k optimu mají signály maximální entropii, a proto jsou nezávislé, což zajišťuje, že extrahované signály jsou také nezávislé. je invertibilní funkce a je signálním modelem. Všimněte si toho, že pokud funkce hustoty pravděpodobnosti modelu zdrojového signálu odpovídá funkci hustoty pravděpodobnosti extrahovaného signálu , pak maximalizace společné entropie maximalizuje také množství vzájemných informací mezi a . Z tohoto důvodu je použití entropie k extrakci nezávislých signálů známé jako infomax . ${\ displaystyle \ mathbf {x}}$${\ displaystyle g}$${\ displaystyle \ mathbf {W}}$${\ displaystyle \ mathbf {Y} = g (\ mathbf {y})}$${\ displaystyle \ mathbf {y} = \ mathbf {Wx}}$${\ displaystyle \ mathbf {W}}$${\ displaystyle \ mathbf {W}}$${\ displaystyle \ mathbf {Y}}$${\ Displaystyle \ mathbf {y} = g^{-1} (\ mathbf {Y})}$${\ displaystyle g}$ ${\ displaystyle p_ {s}}$${\ displaystyle p _ {\ mathbf {y}}}$${\ displaystyle Y}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {Y}}$

Uvažujme entropii vektorové proměnné , kde je množina signálů extrahovaná rozmixovací maticí . Pro konečnou sadu hodnot vzorkovaných z distribuce s pdf lze entropii odhadnout jako: ${\ displaystyle \ mathbf {Y} = g (\ mathbf {y})}$${\ displaystyle \ mathbf {y} = \ mathbf {Wx}}$${\ displaystyle \ mathbf {W}}$${\ displaystyle p _ {\ mathbf {y}}}$${\ displaystyle \ mathbf {Y}}$

${\ Displaystyle H (\ mathbf {Y}) =-{\ frac {1} {N}} \ sum _ {t = 1}^{N} \ ln p _ {\ mathbf {Y}} (\ mathbf {Y } ^{t})}$

Společný soubor pdf lze ukázat jako související se společným souborem PDF extrahovaných signálů pomocí vícerozměrné formy: ${\ displaystyle p _ {\ mathbf {Y}}}$${\ displaystyle p _ {\ mathbf {y}}}$

${\ displaystyle p _ {\ mathbf {Y}} (Y) = {\ frac {p _ {\ mathbf {y}} (\ mathbf {y})} {| {\ frac {\ partial \ mathbf {Y}} { \ částečné \ mathbf {y}}} |}}}}$

kde je jakobijská matice . Máme a je pdf předpokládané pro zdrojové signály , proto ${\ Displaystyle \ mathbf {J} = {\ frac {\ částečné \ mathbf {Y}} {\ částečné \ mathbf {y}}}}$${\ Displaystyle | \ mathbf {J} | = g '(\ mathbf {y})}$${\ displaystyle g '}$${\ displaystyle g '= p_ {s}}$

${\ Displaystyle p _ {\ mathbf {Y}} (Y) = {\ frac {p _ {\ mathbf {y}} (\ mathbf {y})} {| {\ frac {\ partial \ mathbf {Y}} { \ částečné \ mathbf {y}}} |}}} = {\ frac {p _ {\ mathbf {y}} (\ mathbf {y})} {p _ {\ mathbf {s}} (\ mathbf {y})} }}$

proto,

${\ Displaystyle H (\ mathbf {Y}) =-{\ frac {1} {N}} \ sum _ {t = 1}^{N} \ ln {\ frac {p _ {\ mathbf {y}} ( \ mathbf {y})} {p _ {\ mathbf {s}} (\ mathbf {y})}}}$

Víme, že kdy , má rovnoměrné rozdělení a je maximalizováno. Od té doby ${\ displaystyle p _ {\ mathbf {y}} = p_ {s}}$${\ displaystyle p _ {\ mathbf {Y}}}$${\ displaystyle H ({\ mathbf {Y}})}$

${\ Displaystyle p _ {\ mathbf {y}} (\ mathbf {y}) = {\ frac {p _ {\ mathbf {x}} (\ mathbf {x})} {| {\ frac {\ partial \ mathbf { y}} {\ partial \ mathbf {x}}} |}}} = {\ frac {p _ {\ mathbf {x}} (\ mathbf {x})} {| \ mathbf {W} |}}}$

kde je absolutní hodnota determinantu nemísící matice . Proto, ${\ displaystyle | \ mathbf {W} |}$${\ displaystyle \ mathbf {W}}$

${\ Displaystyle H (\ mathbf {Y}) =-{\ frac {1} {N}} \ sum _ {t = 1}^{N} \ ln {\ frac {p _ {\ mathbf {x}} ( \ mathbf {x} ^{t})} {| \ mathbf {W} | p _ {\ mathbf {s}} (\ mathbf {y} ^{t})}}}$

tak,

${\ Displaystyle H (\ mathbf {Y}) = {\ frac {1} {N}} \ sum _ {t = 1}^{N} \ ln p _ {\ mathbf {s}} (\ mathbf {y} ^{t})+\ ln | \ mathbf {W} |+H (\ mathbf {x})}$

protože a maximalizace neovlivňuje , můžeme tedy funkci maximalizovat ${\ Displaystyle H (\ mathbf {x}) =-{\ frac {1} {N}} \ sum _ {t = 1}^{N} \ ln p _ {\ mathbf {x}} (\ mathbf {x } ^{t})}$${\ displaystyle \ mathbf {W}}$${\ displaystyle H _ {\ mathbf {x}}}$

${\ Displaystyle h (\ mathbf {Y}) = {\ frac {1} {N}} \ sum _ {t = 1}^{N} \ ln p _ {\ mathbf {s}} (\ mathbf {y} ^{t})+\ ln | \ mathbf {W} |}$

k dosažení nezávislosti extrahovaného signálu.

Pokud existují M okrajové soubory pdf společného modelu, jsou nezávislé a pro zdrojové signály používají běžně super-gaussovský model pdf , pak máme ${\ displaystyle p _ {\ mathbf {s}}}$${\ Displaystyle p _ {\ mathbf {s}} = (1- \ tanh (\ mathbf {s})^{2})}$

${\ Displaystyle h (\ mathbf {Y}) = {\ frac {1} {N}} \ sum _ {i = 1}^{M} \ sum _ {t = 1}^{N} \ ln (1 -\ tanh (\ mathbf {w_ {i}^{T} x^{t}})^{2})+\ ln | \ mathbf {W} |}$

V součtu, vzhledem k pozorované směsi signálů , odpovídající sadě extrahovaných signálů a modelu zdrojového signálu , můžeme najít optimální matici míchání a učinit extrahované signály nezávislé a ne gaussovské. Stejně jako v situaci sledování projekce můžeme použít metodu sestupu gradientu k nalezení optimálního řešení míchání matice. ${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {y}}$${\ displaystyle p _ {\ mathbf {s}} = g '}$${\ displaystyle \ mathbf {W}}$

Na základě odhadu maximální pravděpodobnosti

Odhad maximální pravděpodobnosti (MLE) je standardní statistický nástroj pro hledání hodnot parametrů (např. Míchací matice), které poskytují nejlepší přizpůsobení některých dat (např. Extrahovaných signálů) danému modelu (např. Předpokládaná společná funkce hustoty pravděpodobnosti (pdf)zdrojových signálů). ${\ displaystyle \ mathbf {W}}$${\ displaystyle y}$${\ displaystyle p_ {s}}$

ML „Model“ zahrnuje specifikaci pdf, který je v tomto případě pdf neznámých zdrojových signálů . Pomocí ML ICA je cílem najít nemísící matici, která poskytne extrahované signály se společným pdf co nejvíce podobným společnému pdf neznámých zdrojových signálů . ${\ displaystyle p_ {s}}$${\ displaystyle s}$${\ displaystyle y = \ mathbf {W} x}$${\ displaystyle p_ {s}}$${\ displaystyle s}$

MLE je tedy založen na předpokladu, že pokud je model pdf a parametry modelu správné, měla by být získána vysoká pravděpodobnost pro data, která byla skutečně pozorována. Naopak, pokud je daleko od správných hodnot parametrů, pak by se očekávala nízká pravděpodobnost pozorovaných dat. ${\ displaystyle p_ {s}}$${\ displaystyle \ mathbf {A}}$${\ displaystyle x}$${\ displaystyle \ mathbf {A}}$

Pomocí MLE nazýváme pravděpodobnost pozorovaných dat pro danou sadu hodnot modelových parametrů (např. Pdf a matice ) pravděpodobnost hodnot modelových parametrů vzhledem k pozorovaným datům. ${\ displaystyle p_ {s}}$${\ displaystyle \ mathbf {A}}$

Definujeme pravděpodobnosti funkci z : ${\ displaystyle \ mathbf {L (W)}}$${\ displaystyle \ mathbf {W}}$

${\ Displaystyle \ mathbf {L (W)} = p_ {s} (\ mathbf {W} x) | \ det \ mathbf {W} |.}$

To se rovná hustotě pravděpodobnosti v , od . ${\ displaystyle x}$${\ displaystyle s = \ mathbf {W} x}$

Pokud tedy chceme najít to, které s největší pravděpodobností generovalo pozorované směsi z neznámých zdrojových signálů pomocí pdf, pak potřebujeme najít pouze to, co maximalizuje pravděpodobnost . Unmixovací matice, která maximalizuje rovnici, je známá jako MLE optimální matice pro míchání. ${\ displaystyle \ mathbf {W}}$${\ displaystyle x}$${\ displaystyle s}$${\ displaystyle p_ {s}}$${\ displaystyle \ mathbf {W}}$ ${\ displaystyle \ mathbf {L (W)}}$

Je běžnou praxí používat pravděpodobnost protokolu , protože to se snáze vyhodnotí. Protože logaritmus je monotónní funkce, maximalizace funkce také maximalizuje jeho logaritmus . To nám umožňuje vzít výše uvedený logaritmus rovnice, který poskytuje funkci pravděpodobnosti protokolu${\ displaystyle \ mathbf {W}}$${\ displaystyle \ mathbf {L (W)}}$${\ displaystyle \ ln \ mathbf {L (W)}}$

${\ Displaystyle \ ln \ mathbf {L (W)} = \ sum _ {i} \ sum _ {t} \ ln p_ {s} (w_ {i}^{T} x_ {t})+N \ ln | \ det \ mathbf {W} |}$

Pokud za zdrojové signály nahradíme běžně používaný high- Kurtosis model pdf, máme ${\ Displaystyle p_ {s} = (1- \ tanh (s)^{2})}$

${\ Displaystyle \ ln \ mathbf {L (W)} = {1 \ over N} \ sum _ {i}^{M} \ sum _ {t}^{N} \ ln (1- \ tanh (w_ { i}^{T} x_ {t})^{2})+\ ln | \ det \ mathbf {W} |}$

Tato matice, která maximalizuje tuto funkci, je odhad maximální pravděpodobnosti . ${\ displaystyle \ mathbf {W}}$

Historie a pozadí

Raný obecný rámec pro analýzu nezávislých komponent zavedli Jeanny Hérault a Bernard Ans z roku 1984, dále jej rozvinul Christian Jutten v letech 1985 a 1986 a zpřesnil Pierre Comon v roce 1991 a propagoval ve svém příspěvku z roku 1994. V roce 1995 Tony Bell a Terry Sejnowski představili rychlý a účinný ICA algoritmus založený na infomaxu , principu, který zavedl Ralph Linsker v roce 1987.

V literatuře je k dispozici mnoho algoritmů, které dělají ICA. Z velké části používaný, a to i v průmyslových aplikacích, je algoritmus FastICA, vyvinutý společností Hyvärinen a Oja, který používá kurtózu jako nákladovou funkci. Další příklady se týkají spíše separace slepých zdrojů, kde se používá obecnější přístup. Například lze zrušit předpoklad nezávislosti a oddělit vzájemně korelované signály, tedy statisticky „závislé“ signály. Sepp Hochreiter a Jürgen Schmidhuber ukázali, jak získat nelineární ICA nebo separaci zdroje jako vedlejší produkt regularizace (1999). Jejich metoda nevyžaduje apriorní znalosti o počtu nezávislých zdrojů.

Aplikace

ICA lze rozšířit o analýzu nefyzických signálů. Například ICA byla použita k objevování diskusních témat v pytli archivů seznamů novinek.

Některé aplikace ICA jsou uvedeny níže:

Analýza nezávislých komponent v EEGLAB

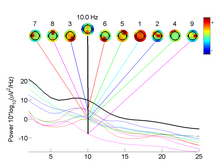
• optické zobrazování neuronů
• třídění neuronových špiček
• rozpoznávání obličejů
• modelování receptivních polí primárních zrakových neuronů
• předpovídání cen na akciových trzích
• komunikace mobilního telefonu
• barevná detekce zralosti rajčat
• odstraňování artefaktů, například mrknutí očí, z dat EEG .
• analýza změn v genové expresi v průběhu času v experimentech sekvenování RNA s jednou buňkou .
• studie klidové stavové sítě mozku.
• astronomie a kosmologie

Viz také

Poznámky

Reference

• Comon, Pierre (1994): "Analýza nezávislých komponent: nový koncept?" „ Zpracování signálu , 36 (3): 287–314 (Původní dokument popisující koncept ICA)
• Hyvärinen, A .; Karhunen, J .; Oja, E. (2001): Independent Component Analysis , New York: Wiley, ISBN  978-0-471-40540-5 ( úvodní kapitola )
• Hyvärinen, A .; Oja, E. (2000): „Analýza nezávislých komponent: Algoritmy a aplikace“ , Neural Networks , 13 (4-5): 411-430. (Technický, ale pedagogický úvod).
• Comon, P .; Jutten C., (2010): Handbook of Blind Source Separation, Independent Component Analysis and Applications. Academic Press, Oxford UK. ISBN  978-0-12-374726-6
• Lee, T.-W. (1998): Analýza nezávislých komponent: Teorie a aplikace , Boston, Mass: Kluwer Academic Publishers, ISBN  0-7923-8261-7
• Acharyya, Ranjan (2008): A New Approach for Blind Source Separation of Convolutive Sources-Wavelet Based Separation Using Shrinkage Function ISBN  3-639-07797-0 ISBN  978-3639077971 (Tato kniha se zaměřuje na učení bez dozoru s oddělením slepého zdroje)

externí odkazy

• Co je analýza nezávislých komponent? od Aapo Hyvärinena
• Analýza nezávislých komponent: návod od Aapo Hyvärinena
• Výukový program o analýze nezávislých komponent
• FastICA jako balíček pro Matlab, v jazyce R, C ++
• ICALAB Toolboxes for Matlab, vyvinutý ve společnosti RIKEN
• High Performance Signal Analysis Toolkit provides C ++ implementations of FastICA and Infomax
• Sada nástrojů ICA Nástroje Matlab pro ICA s Bell-Sejnowski, Molgedey-Schuster a střední poli ICA. Vyvinuto na DTU.
• Ukázka problému s koktejlovou párty
• EEGLAB Toolbox ICA EEG pro Matlab, vyvinutý na UCSD.
• FMRLAB Toolbox ICA fMRI pro Matlab, vyvinutý na UCSD
• MELODIC , součást softwarové knihovny FMRIB .
• Diskuse o ICA v kontextu biomedicínské reprezentace tvarů
• Algoritmus FastICA, CuBICA, JADE a TDSEP pro Python a další ...
• Skupina ICA Toolbox a Fusion ICA Toolbox
• Výukový program: Použití ICA k čištění signálů EEG