Lévyho let - Lévy flight

Lévy letu je náhodná procházka , v nichž nevlastní délky mají Lévy distribuce , je rozdělení pravděpodobnosti , které je těžké ocasem . Pokud jsou kroky definovány jako procházka v prostoru o rozměru větším než jeden, provedené kroky jsou v izotropních náhodných směrech. Pozdější vědci rozšířili používání pojmu „Lévy let“ tak, aby zahrnoval i případy, kdy se náhodná procházka odehrává spíše na diskrétní mřížce než na souvislém prostoru.

Termín „Lévy let“ vytvořil Benoît Mandelbrot , který ho použil pro jednu konkrétní definici rozdělení velikostí kroků. Termín Cauchyho let použil pro případ, kdy je distribucí velikostí kroků Cauchyho distribuce , a Rayleighovým letem pro případ, kdy je distribuce normální distribuce (což není příkladem těžce sledovaného rozdělení pravděpodobnosti).

Zvláštní případ, pro který Mandelbrot používá, termín „dávka letu“ je definován funkcí přežil (běžně známý jako funkce přežití) distribuce kroků velikostech, U , být

${\ Displaystyle \ Pr (U> u) = {\ begin {cases} 1 &: \ u <1, \\ u^{-D} &: \ u \ geq 1. \ end {cases}}}$

Zde D je parametr související s fraktální dimenzí a distribuce je konkrétním případem Paretovy distribuce .

Vlastnosti

Lévy lety jsou podle konstrukce Markovovy procesy . U obecných distribucí velikosti kroku splňujících podmínky podobné síle má vzdálenost od počátku náhodné procházky po velkém počtu kroků tendenci ke stabilnímu rozdělení díky zobecněné centrální limitní větě , což umožňuje mnoha procesům být modelovány pomocí letů Lévy.

Hustoty pravděpodobnosti pro částice procházející Levyho letem lze modelovat pomocí zobecněné verze Fokker -Planckovy rovnice , která se obvykle používá k modelování Brownova pohybu . Rovnice vyžaduje použití zlomkových derivátů . Pro délky skoku, které mají symetrické rozdělení pravděpodobnosti, má rovnice jednoduchou formu z hlediska Rieszovy zlomkové derivace . V jedné dimenzi rovnice zní jako

${\ Displaystyle {\ frac {\ částečné \ varphi (x, t)} {\ částečné t}} =-{\ frac {\ částečné {\ částečné x}} f (x, t) \ varphi (x, t )+\ gamma {\ frac {\ částečné ^{\ alpha} \ varphi (x, t)} {\ částečné | x | ^{\ alpha}}}}$

kde γ je konstanta podobná difúzní konstantě, α je parametr stability a f (x, t) je potenciál. Derivát Riesz lze chápat z hlediska jeho Fourierovy transformace .

${\ Displaystyle F_ {k} \ left [{\ frac {\ partial ^{\ alpha} \ varphi (x, t)} {\ partial | x | ^{\ alpha}}} \ \ right] =-| k | ^{\ alpha} F_ {k} [\ varphi (x, t)]}$

To lze snadno rozšířit na více rozměrů.

Další důležitou vlastností Lévyho letu jsou odchylné odchylky ve všech případech kromě α  = 2, tj. Brownova pohybu. Obecně platí, že θ zlomkový moment rozdělení se rozchází, pokud α  ≤   θ . Taky,

${\ Displaystyle \ langle | x |^{\ theta} \ rangle \ propto t^{\ theta /\ alpha} {\ text {if}} \ theta <\ alpha.}$

Exponenciální škálování délek kroků dává lévským letům vlastnost neměnnou v měřítku a používají se k modelování dat, která vykazují shlukování.

Obrázek 1. Příklad 1000 kroků letu Lévyho ve dvou rozměrech. Počátek pohybu je v [0,0], úhlový směr je rovnoměrně rozložen a velikost kroku je rozdělena podle Lévyho (tj. Stabilního ) rozdělení s α  = 1 a β  = 0, což je Cauchyovo rozdělení . Všimněte si přítomnosti velkých skoků na místě ve srovnání s Brownovým pohybem znázorněným na obrázku 2.

Obrázek 2. Příklad 1000 kroků aproximace typu Brownova pohybu Lévyho letu ve dvou dimenzích. Původ pohybu je u [0, 0], úhlová směr rovnoměrně rozdělí a velikost kroku je distribuován podle (tj Lévy stabilní ) rozdělení s α  = 2 a p  = 0 ( tj, v normální distribuce ).

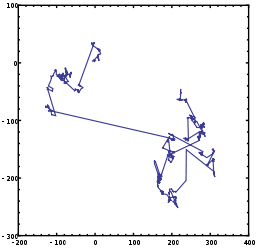
Aplikace

Definice Lévyho letu vychází z matematiky související s teorií chaosu a je užitečná při stochastických měřeních a simulacích pro náhodné nebo pseudonáhodné přírodní jevy. Mezi příklady patří analýza údajů o zemětřesení , finanční matematika , kryptografie , analýza signálů a mnoho aplikací v astronomii , biologii a fyzice .

Další aplikací je Lévy hypotéza o hledání potravy . Když žraloci a další oceánští predátoři nemohou najít potravu, opustí Brownův pohyb , náhodný pohyb pozorovaný ve vířících molekulách plynu, pro Lévyho let - kombinaci dlouhých trajektorií a krátkých, náhodných pohybů nacházejících se v turbulentních tekutinách. Výzkumníci analyzovali více než 12 milionů pohybů zaznamenaných za 5 700 dní u 55 zvířat označených data loggerem ze 14 druhů predátorů oceánů v Atlantském a Tichém oceánu, včetně žraloků hedvábných , tuňáka žlutoploutvého , marlina obecného a mečouna. Data ukázala, že lety Lévy proložené Brownovým pohybem mohou popsat lovecké vzorce zvířat. Ptáci a další zvířata (včetně lidí) sledují cesty, které byly modelovány pomocí Lévyho letu (např. Při hledání potravy). Biologická letová data mohou být zjevně napodobována jinými modely, jako jsou kompozitní korelované náhodné procházky, které rostou napříč měřítky, aby se sbíhaly při optimálních procházkách Lévy. Složené Brownianovy procházky lze jemně vyladit na teoreticky optimální Lévyho procházky, ale nejsou tak účinné jako Lévyho hledání ve většině typů krajin, což naznačuje, že selekční tlak pro vlastnosti Lévyho chůze je pravděpodobnější než víceúrovňové normální difúzní vzory.

Efektivní směrování v síti lze provádět pomocí odkazů s distribucí délky letu Levy se specifickými hodnotami alfa.

Viz také

• Anomální difúze
• Rozložení tuku
• Silně ocasní distribuce
• Lévyho proces
• Lévy alfa-stabilní distribuce
• Lévy hypotéza hledání letu

Poznámky

Reference

• Mandelbrot, Benoit B. (1982). Fraktální geometrie přírody (Aktualizováno a srpen. Ed.). New York: WH Freeman. ISBN 0-7167-1186-9. OCLC  7876824 .

Další čtení

• Viswanathan, G .; Bartumeus, F .; v. Buldyrev, S .; Catalan, J .; Fulco, U .; Havlin, S .; Da Luz, M .; Lyra, M .; Raposo, E .; Eugene Stanley, H. (2002). „Lévy letové náhodné vyhledávání biologických jevů“. Physica A: Statistická mechanika a její aplikace . 314 (1–4): 208–213. Bibcode : 2002PhyA..314..208V . doi : 10,1016/S0378-4371 (02) 01157-3 .
• Viswanathan, G .; Afanasyev, V .; Buldyrev, S .; Havlin, S .; Daluz, M .; Raposo, E .; Stanley, H. (2000). „Lévy lety v náhodném vyhledávání“. Physica A: Statistická mechanika a její aplikace . 282 (1–2): 1–12. Bibcode : 2000PhyA..282 .... 1V . doi : 10,1016/S0378-4371 (00) 00071-6 .
• Cheng, Z .; Savit, R. (1987). „Fraktální a nefraktální chování při letech Levy“ (PDF) . Journal of Mathematical Physics . 28 (3): 592. Bibcode : 1987JMP .... 28..592C . doi : 10,1063/1,527644 . hdl : 2027,42/70735 .
• Shlesinger, Michael F .; Klafter, Joseph; Zumofen, Gert (prosinec 1999). „Nahoře, dole a za Brownovým pohybem“ (PDF) . American Journal of Physics . 67 (12): 1253–1259. Bibcode : 1999AmJPh..67.1253S . doi : 10,1119/1,19112 . Archivováno z originálu (PDF) dne 2012-03-28.

externí odkazy

• Srovnání obrazů Jacksona Pollocka s letovým modelem Lévy