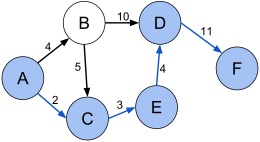
Problém s nejkratší cestou - Shortest path problem

V teorii grafů je nejkratším problémem cesty problém nalezení cesty mezi dvěma vrcholy (nebo uzly) v grafu tak, aby byl minimalizován součet hmotností jeho základních hran.

Problém nalezení nejkratší cesty mezi dvěma křižovatkami na cestovní mapě lze modelovat jako speciální případ problému s nejkratší cestou v grafech, kde vrcholy odpovídají křižovatkám a hrany odpovídají úsekům silnice, každý vážený délkou cesty segment.

Definice

Problém nejkratší cesty lze definovat pro grafy, ať už neorientované , směrované nebo smíšené . Zde je definována pro neorientované grafy; pro směrované grafy definice cesty vyžaduje, aby po sobě jdoucí vrcholy byly spojeny vhodnou směrovanou hranou.

Dva vrcholy sousedí, když oba dopadají na společnou hranu. Cesta v undirected grafu je posloupnost vrcholů tak, že sousedí s k . Taková cesta se nazývá cesta délky od do . (Jsou to proměnné; jejich číslování zde souvisí s jejich pozicí v pořadí a nemusí se vztahovat k žádnému kanonickému označování vrcholů.) ${\ displaystyle P = (v_ {1}, v_ {2}, \ ldots, v_ {n}) \ in V \ times V \ times \ cdots \ times V}$${\ displaystyle v_ {i}}$${\ displaystyle v_ {i + 1}}$${\ displaystyle 1 \ leq i <n}$${\ displaystyle P}$${\ displaystyle n-1}$${\ displaystyle v_ {1}}$${\ displaystyle v_ {n}}$${\ displaystyle v_ {i}}$

Nechť je okrajový incident pro oba a . Vzhledem k funkci vážení se skutečnou hodnotou a neusměrněnému (jednoduchému) grafu je nejkratší cestou od do cesta (kde a ), která ve všech možných případech minimalizuje součet Když má každá hrana v grafu jednotkovou hmotnost nebo je to ekvivalentní nalezení cesty s nejmenším počtem hran. ${\ displaystyle e_ {i, j}}$${\ displaystyle v_ {i}}$${\ displaystyle v_ {j}}$${\ displaystyle f: E \ rightarrow \ mathbb {R}}$${\ displaystyle G}$${\ displaystyle v}$${\ displaystyle v '}$${\ displaystyle P = (v_ {1}, v_ {2}, \ ldots, v_ {n})}$${\ displaystyle v_ {1} = v}$${\ displaystyle v_ {n} = v '}$${\ displaystyle n}$${\ displaystyle \ sum _ {i = 1} ^ {n-1} f (e_ {i, i + 1}).}$${\ displaystyle f: E \ rightarrow \ {1 \}}$

Problém se také někdy nazývá problém s nejkratší cestou jednoho páru , abychom jej odlišili od následujících variant:

• Problém nejkratší cesty s jedním zdrojem , ve kterém musíme najít nejkratší cesty od zdrojového vrcholu v ke všem ostatním vrcholům v grafu.
• Problém nejkratší cesty s jedním cílem , ve kterém musíme najít nejkratší cesty ze všech vrcholů v směrovaném grafu k jednomu cílovému vrcholu v . To lze snížit na problém s nejkratší cestou jednoho zdroje obrácením oblouků v směrovaném grafu.
• Problém nejkratší cesty všech párů , ve kterém musíme najít nejkratší cesty mezi každou dvojicí vrcholů v , v ' v grafu.

Tyto zobecnění mají podstatně efektivnější algoritmy než zjednodušující přístup ke spuštění algoritmu nejkratší cesty s jedním párem na všech příslušných párech vrcholů.

Algoritmy

Nejdůležitějšími algoritmy pro řešení tohoto problému jsou:

• Dijkstrův algoritmus řeší problém s nejkratší cestou jednoho zdroje s nezápornou váhou hrany.
• Algoritmus Bellman-Ford řeší problém jednoho zdroje, pokud mohou být okrajové váhy záporné.
• Vyhledávací algoritmus * řeší nejkratší cestu jednoho páru pomocí heuristiky, aby se pokusil zrychlit hledání.
• Algoritmus Floyd – Warshall řeší všechny páry nejkratších cest.
• Johnsonův algoritmus řeší všechny páry nejkratších cest a může být rychlejší než Floyd – Warshall na řídkých grafech .
• Algoritmus Viterbi řeší problém nejkratší stochastické dráhy s další pravděpodobnostní váhou na každém uzlu.

Další algoritmy a související hodnocení lze nalézt v Cherkassky, Goldberg & Radzik (1996) .

Nejkratší cesty jednoho zdroje

Neorientované grafy

Závaží	Časová složitost	Autor
ℝ +	O ( V 2 )	Dijkstra 1959
ℝ +	O (( E  +  V ) log  V )	Johnson 1977 ( binární halda )
ℝ +	O ( E  +  V  log  V )	Fredman & Tarjan 1984 ( Fibonacciho halda )
ℕ	O ( E )	Thorup 1999 (vyžaduje násobení v konstantním čase)

Nevážené grafy

Algoritmus	Časová složitost	Autor
Šířka první vyhledávání	O ( E  +  V )

Směrované acyklické grafy (DAG)

Algoritmus využívající topologické třídění může vyřešit problém nejkratší cesty s jedním zdrojem v čase Θ ( E + V ) v libovolně vážených DAG.

Směrované grafy s nezápornými váhami

Následující tabulka je převzata od Schrijvera (2004) s některými opravami a dodatky. Zelené pozadí označuje asymptoticky nejlépe vázané v tabulce; L je maximální délka (nebo hmotnost) mezi všemi hranami, za předpokladu celočíselné hmotnosti hran.

Závaží	Algoritmus	Časová složitost	Autor
ℝ		O ( V 2 EL )	Ford 1956
ℝ	Algoritmus Bellman-Ford	O ( VE )	Shimbel 1955 , Bellman 1958 , Moore 1959
ℝ		O ( V 2  log  V )	Dantzig 1960
ℝ	Dijkstrův algoritmus se seznamem	O ( V 2 )	Leyzorek a kol. 1957 , Dijkstra 1959 , Minty (viz Pollack & Wiebenson 1960 ), Whiting & Hillier 1960
ℝ	Dijkstrův algoritmus s binární hromadou	O (( E  +  V ) log  V )	Johnson 1977
ℝ	Dijkstrův algoritmus s haldy Fibonacci	O ( E  +  V  log  V )	Fredman & Tarjan 1984 , Fredman & Tarjan 1987
ℕ	Dialův algoritmus ( Dijkstrův algoritmus využívající frontu s kbelíky L )	O ( E  +  LV )	Vytočit 1969
		O ( E  log log  L )	Johnson 1981 , Karlsson & Poblete 1983
	Gabowův algoritmus	O ( E  log E / V  L )	Gabow 1983 , Gabow 1985
		O ( E  +  V √ log L )	Ahuja et al. 1990
	Thorup	O ( E  +  V  log log  V )	Thorup 2004

Směrované grafy s libovolnými váhami bez negativních cyklů

Závaží	Algoritmus	Časová složitost	Autor
ℝ		O ( V 2 EL )	Ford 1956
ℝ	Algoritmus Bellman-Ford	O ( VE )	Shimbel 1955 , Bellman 1958 , Moore 1959
ℝ	Johnson-Dijkstra s binární hromadou	O ( V  ( E  + log  V ))	Johnson 1977
ℝ	Johnson-Dijkstra s haldy Fibonacci	O ( V  ( E  + log  V ))	Fredman & Tarjan 1984 , Fredman & Tarjan 1987 , upraveno po Johnsonovi 1977
ℕ	Johnsonova technika aplikovaná na Dialův algoritmus	O ( V  ( E  +  L ))	Dial 1969 , upraveno po Johnsonovi 1977

Rovinné směrované grafy s libovolnými váhami

Nejkratší cesty všech párů

Problém s nejkratší cestou všech párů najde nejkratší cesty mezi každou dvojicí vrcholů v , v ' v grafu. Problém nejkratších cest všech párů pro nevážené směrované grafy představil Shimbel (1953) , který poznamenal, že by jej bylo možné vyřešit lineárním počtem násobení matic, které zabere celkovou dobu O ( V ⁴ ) .

Neusměrněný graf

Závaží	Časová složitost	Algoritmus
ℝ +	O ( V 3 )	Floyd-Warshallův algoritmus
${\ displaystyle \ {1, \ infty \}}$	${\ displaystyle O (V ^ {\ omega} \ log V)}$	Seidelův algoritmus (očekávaná doba provozu)
ℕ	${\ displaystyle O (V ^ {3} / 2 ^ {\ Omega (\ log n) ^ {1/2}})}$	Williams 2014
ℝ +	O ( EV  log α ( E , V ))	Pettie & Ramachandran 2002
ℕ	O ( EV )	Thorup 1999 aplikovaný na každý vrchol (vyžaduje násobení v konstantním čase).

Směrovaný graf

Závaží	Časová složitost	Algoritmus
ℝ (žádné negativní cykly)	O ( V 3 )	Floyd-Warshallův algoritmus
ℕ	${\ displaystyle O (V ^ {3} / 2 ^ {\ Omega (\ log n) ^ {1/2}})}$	Williams 2014
ℝ (žádné negativní cykly)	O ( EV  +  V 2  log  V )	Johnson – Dijkstra
ℝ (žádné negativní cykly)	O ( EV  +  V 2  log log  V )	Pettie 2004
ℕ	O ( EV  +  V 2  log log  V )	Hagerup 2000

Aplikace

Algoritmy nejkratší cesty se používají k automatickému vyhledání směrů mezi fyzickými místy, jako jsou směry jízdy na webech s webovými mapami, jako jsou MapQuest nebo Google Maps . Pro tuto aplikaci jsou k dispozici rychlé specializované algoritmy.

Pokud jeden představuje nedeterministický abstraktní stroj jako graf, kde vrcholy popisují stavy a hrany popisují možné přechody, lze použít algoritmy nejkratší cesty k nalezení optimální posloupnosti voleb k dosažení určitého stavu cíle nebo k stanovení nižších mezí času potřebného k dosáhnout daného stavu. Pokud například vrcholy představují stavy skládačky jako Rubikova kostka a každá nasměrovaná hrana odpovídá jednomu tahu nebo otočení, lze k nalezení řešení, které využívá minimální možný počet tahů, použít algoritmy nejkratší cesty.

V síťovém nebo telekomunikačním myšlení se tento problém s nejkratší cestou někdy nazývá problém cesty s min. Zpožděním a obvykle je spojen s problémem s nejširší cestou . Algoritmus může například hledat nejkratší (nejmenší zpoždění) nejširší cestu nebo nejširší nejkratší (nejmenší zpoždění) cestu.

Bezstarostnější aplikací jsou hry „ šesti stupňů oddělení “, které se snaží najít nejkratší cestu v grafech, jako jsou filmové hvězdy, které se objevují ve stejném filmu.

Mezi další aplikace, často studované v operačním výzkumu , patří rozložení závodů a zařízení, robotika , doprava a návrh VLSI .

Silniční sítě

Silniční síť lze považovat za graf s kladnými váhami. Uzly představují silniční křižovatky a každá hrana grafu je spojena s úsekem silnice mezi dvěma křižovatkami. Váha hrany může odpovídat délce příslušného segmentu silnice, času potřebnému k projetí segmentu nebo nákladům na přejetí segmentu. Pomocí směrovaných hran je také možné modelovat jednosměrné ulice. Takové grafy jsou zvláštní v tom smyslu, že některé hrany jsou pro cestování na dlouhé vzdálenosti důležitější než jiné (např. Dálnice). Tato vlastnost byla formována pomocí pojmu dálniční dimenze. Existuje velké množství algoritmů, které využívají tuto vlastnost, a jsou proto schopné vypočítat nejkratší cestu mnohem rychleji, než by to bylo možné v obecných grafech.

Všechny tyto algoritmy fungují ve dvou fázích. V první fázi je graf předzpracován bez znalosti zdrojového nebo cílového uzlu. Druhá fáze je fáze dotazu. V této fázi jsou známy zdrojový a cílový uzel. Myšlenka je, že silniční síť je statická, takže fázi předzpracování lze provést jednou a použít ji pro velké množství dotazů na stejné silniční síti.

Algoritmus s nejrychleji známou dobou dotazu se nazývá označení hubu a je schopen vypočítat nejkratší cestu v silničních sítích Evropy nebo USA za zlomek mikrosekundy. Další techniky, které byly použity, jsou:

• ALT ( vyhledávání A * , orientační body a nerovnost trojúhelníků )
• Vlajky oblouku
• Hierarchie kontrakcí
• Směrování tranzitního uzlu
• Prořezávání na základě dosahu
• Značení
• Štítky nábojů

Související problémy

Problémy s nejkratší cestou ve výpočetní geometrii najdete v euklidovské nejkratší cestě .

Problém obchodního cestujícího je problém najít nejkratší cestu, která projde každým vrcholem přesně jednou a vrátí se na začátek. Na rozdíl od problému s nejkratší cestou, který lze vyřešit v polynomiálním čase v grafech bez negativních cyklů, je problém obchodního cestujícího NP-úplný a jako takový se má za to, že není efektivně řešitelný pro velké soubory dat (viz P = NP problém ). Problém nalezení nejdelší cesty v grafu je také NP-úplný.

Cestovatel Problém Kanadský a stochastický nejkratší cesta problémem jsou zevšeobecňování, kde buď grafu není zcela známo, že navrhovatele, se mění v čase, nebo tam, kde akce (Procházení) jsou pravděpodobnostní.

Nejkratší vícenásobně odpojená cesta je reprezentací sítě primitivních cest v rámci teorie Reptation .

Nejširší cesta problém hledá cestu, tak, že minimální označení jakéhokoliv hrany je tak velký, jak je to možné.

Strategické nejkratší cesty

Někdy mají hrany v grafu osobnosti: každá hrana má svůj vlastní sobecký zájem. Příkladem je komunikační síť, ve které je každá hrana počítač, který možná patří jiné osobě. Různé počítače mají různé přenosové rychlosti, takže každá hrana v síti má číselnou váhu rovnou počtu milisekund potřebných k přenosu zprávy. Naším cílem je odeslat zprávu mezi dvěma body v síti v co nejkratším čase. Pokud známe dobu přenosu každého počítače (váhu každé hrany), můžeme použít standardní algoritmus nejkratších cest. Pokud neznáme doby přenosu, musíme požádat každý počítač, aby nám sdělil svůj čas přenosu. Ale počítače mohou být sobecké: počítač nám může říct, že jeho doba přenosu je velmi dlouhá, takže ho nebudeme obtěžovat svými zprávami. Možným řešením tohoto problému je použití varianty mechanismu VCG , která dává počítačům motivaci odhalit jejich skutečné váhy.

Formulace lineárního programování

Níže je uvedena přirozená formulace lineárního programování pro problém s nejkratší cestou. Je to velmi jednoduché ve srovnání s většinou ostatních použití lineárních programů v diskrétní optimalizaci , nicméně to ilustruje připojení k jiným konceptům.

Vzhledem k orientovanému grafu ( V , A ) se zdrojovým uzlem s , cílovým uzlem t a cenou w _ij pro každou hranu ( i , j ) v A zvažte program s proměnnými x _ij

minimalizovat předmět a pro vše i ,${\ displaystyle \ sum _ {ij \ v A} w_ {ij} x_ {ij}}$${\ displaystyle x \ geq 0}$${\ displaystyle \ sum _ {j} x_ {ij} - \ sum _ {j} x_ {ji} = {\ begin {cases} 1, & {\ text {if}} i = s; \\ - 1, & {\ text {if}} i = t; \\ 0, & {\ text {jinak.}} \ end {případy}}}$

Intuice za tím spočívá v tom, že jde o indikátorovou proměnnou pro to, zda hrana ( i , j ) je součástí nejkratší cesty: 1, když je, a 0, pokud není. Chceme vybrat sadu hran s minimální hmotností, s výhradou omezení, že tato sada tvoří cestu od s do t (představovaná omezením rovnosti: pro všechny vrcholy kromě s a t počet příchozích a odchozích hran, které jsou součástí cesty musí být stejná (tj. měla by to být cesta od s do t). ${\ displaystyle x_ {ij}}$

Toto LP má speciální vlastnost, že je integrální; konkrétněji každé základní optimální řešení (pokud existuje) má všechny proměnné rovné 0 nebo 1 a množinu hran, jejichž proměnné rovné 1 tvoří s - t dipath . Viz Ahuja et al. pro jeden důkaz, ačkoli vznik tohoto přístupu sahá až do poloviny 20. století.

Duální pro tento lineární program je

maximalizovat y _t - y _s předmětem pro všechny ij , y _j - y _i ≤ w _ij

a proveditelné duály odpovídají konceptu konzistentní heuristiky pro algoritmus A * pro nejkratší cesty. Pro jakýkoli proveditelný duální y jsou snížené náklady nezáporné a A * v zásadě spouští Dijkstrův algoritmus o těchto snížených nákladech. ${\ displaystyle w '_ {ij} = w_ {ij} -y_ {j} + y_ {i}}$

Obecný algebraický rámec na semirings: problém algebraické cesty

Mnoho problémů lze formulovat jako formu nejkratší cesty pro některé vhodně substituované představy o přidání podél cesty a přijetí minima. Obecným přístupem k nim je považovat tyto dvě operace za operace semirování . Násobení semiring se provádí podél cesty a přidání je mezi cestami. Tento obecný rámec je známý jako problém algebraické cesty .

Většina klasických algoritmů nejkratší cesty (a nových) může být formulována jako řešení lineárních systémů přes takové algebraické struktury.

V poslední době byl pod hlavičkou oceňovacích algeber vytvořen ještě obecnější rámec pro řešení těchto (a mnohem méně zjevně souvisejících problémů) .

Nejkratší cesta ve stochastických časově závislých sítích

V reálných situacích je dopravní síť obvykle stochastická a časově závislá. Cestující, který denně projíždí spojem, může na tomto spoji zaznamenat různé doby cestování, a to nejen kvůli kolísání poptávky po cestování (matice původu - destinace), ale také kvůli incidentům, jako jsou pracovní zóny, špatné povětrnostní podmínky, nehody a poruchy vozidla . Výsledkem je, že stochastická časově závislá (STD) síť je realističtější reprezentací skutečné silniční sítě ve srovnání s deterministickou.

Navzdory značnému pokroku v průběhu posledního desetiletí zůstává kontroverzní otázkou, jak by měla být definována a identifikována optimální cesta ve stochastických silničních sítích. Jinými slovy, neexistuje žádná jedinečná definice optimální cesty za nejistoty. Jednou z možných a běžných odpovědí na tuto otázku je najít cestu s minimální očekávanou dobou cesty. Hlavní výhodou použití tohoto přístupu je, že efektivní algoritmy nejkratší cesty zavedené pro deterministické sítě lze snadno použít k identifikaci cesty s minimální očekávanou dobou cesty ve stochastické síti. Výsledná optimální cesta identifikovaná tímto přístupem však nemusí být spolehlivá, protože tento přístup neřeší variabilitu doby cestování. Někteří vědci k řešení tohoto problému používají distribuci času cestování místo jeho očekávané hodnoty, aby zjistili rozdělení pravděpodobnosti celkového času cestování pomocí různých optimalizačních metod, jako je dynamické programování a Dijkstrův algoritmus . Tyto metody používají stochastickou optimalizaci , konkrétně stochastické dynamické programování k nalezení nejkratší cesty v sítích s pravděpodobnou délkou oblouku. Koncept spolehlivosti doby cestování se v literatuře z oblasti dopravního výzkumu zaměňuje s variabilitou doby cestování, takže lze obecně říci, že čím vyšší je variabilita doby cestování, tím nižší bude spolehlivost a naopak.

Aby bylo možné přesněji zohlednit spolehlivost doby cestování, byly navrženy dvě společné alternativní definice optimální cesty za nejistoty. Někteří představili koncept nejspolehlivější trasy, jehož cílem je maximalizovat pravděpodobnost příjezdu včas nebo dříve, než je stanovený rozpočet doby cesty. Jiní alternativně předložili koncept spolehlivé dráhy α, na jejímž základě zamýšleli minimalizovat rozpočet doby cesty potřebný k zajištění předem stanovené pravděpodobnosti příjezdu včas.

Viz také

• Obousměrné vyhledávání , algoritmus, který najde nejkratší cestu mezi dvěma vrcholy na směrovaném grafu
• Euklidovská nejkratší cesta
• Síť toku
• K nejkratší směrování cesty
• Násobení matice min-plus
• Hledání cesty
• Překlenutí nejkratší cesty
• Nejkratší strom cesty

Reference

Poznámky

Bibliografie

Další čtení

• Frigioni, D .; Marchetti-Spaccamela, A .; Nanni, U. (1998). Msgstr "Plně dynamický výstup omezený problém s nejkratší cestou jednoho zdroje". Proc. 7. Annu. ACM-SIAM Symp. Diskrétní algoritmy . Atlanta, GA. 212–221. CiteSeerX  10.1.1.32.9856 .
• Dreyfus, SE (říjen 1967). Posouzení některých algoritmů nejkratší cesty (PDF) (zpráva). Projekt Rand. United States Air Force. RM-5433-PR. DTIC AD-661265.