Q -funkce - Q-function

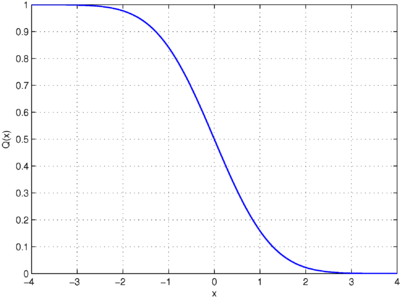
V statistik je Q-funkce je distribuční funkce ocas z normovaného normálního rozdělení . Jinými slovy, je pravděpodobnost, že normální (gaussovská) náhodná proměnná získá hodnotu větší než standardní odchylky. Ekvivalentně je pravděpodobnost, že standardní normální náhodná proměnná nabývá hodnoty větší než . ${\ displaystyle Q (x)}$${\ displaystyle x}$${\ displaystyle Q (x)}$${\ displaystyle x}$

Pokud je Gaussova náhodná proměnná se středem a rozptylem , pak je standardní normální a ${\ displaystyle Y}$${\ Displaystyle \ mu}$${\ Displaystyle \ sigma ^{2}}$${\ Displaystyle X = {\ frac {Y- \ mu} {\ sigma}}}$

${\ Displaystyle P (Y> y) = P (X> x) = Q (x)}$

kde . ${\ Displaystyle x = {\ frac {y- \ mu} {\ sigma}}}$

Jiné definice Q -funkce, z nichž všechny jsou jednoduchými transformacemi normální kumulativní distribuční funkce , se také používají příležitostně.

Vzhledem ke svému vztahu k kumulativní distribuční funkci normálního rozdělení může být Q -funkce také vyjádřena pomocí chybové funkce , která je důležitou funkcí v aplikované matematice a fyzice.

Definice a základní vlastnosti

Formálně je Q -funkce definována jako

${\ Displaystyle Q (x) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {x}^{\ infty} \ exp \ left (-{\ frac {u^{2} } {2}} \ right) \, du.}$

Tím pádem,

${\ Displaystyle Q (x) = 1-Q (-x) = 1- \ Phi (x) \, \ !,}$

kde je kumulativní distribuční funkce standardní normální Gaussovy distribuce . ${\ displaystyle \ Phi (x)}$

Funkci Q lze vyjádřit pomocí chybové funkce nebo doplňkové chybové funkce jako

${\ displaystyle {\ begin {aligned} Q (x) & = {\ frac {1} {2}} \ left ({\ frac {2} {\ sqrt {\ pi}}} \ int _ {x/{ \ sqrt {2}}}^{\ infty} \ exp \ left (-t^{2} \ right) \, dt \ right) \\ & = {\ frac {1} {2}}-{\ frac {1} {2}} \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right) ~~ {\ text {-or -}} \\ & = {\ frac {1} {2}} \ operatorname {erfc} \ left ({\ frac {x} {\ sqrt {2}}} \ right). \ End {aligned}}}$

Alternativní forma funkce Q známá jako Craigův vzorec je po svém objeviteli vyjádřena jako:

${\ Displaystyle Q (x) = {\ frac {1} {\ pi}} \ int _ {0}^{\ frac {\ pi} {2}} \ exp \ left (-{\ frac {x^{ 2}} {2 \ sin ^{2} \ theta}} \ right) d \ theta.}$

Tento výraz je platný pouze pro kladné hodnoty x , ale lze jej použít ve spojení s Q ( x ) = 1 - Q ( - x ) k získání Q ( x ) pro záporné hodnoty. Tato forma je výhodná v tom, že rozsah integrace je pevný a konečný.

Craigův vzorec byl později rozšířen o Behnad (2020) pro Q -funkci součtu dvou nezáporných proměnných, a to následovně:

${\ Displaystyle Q (x+y) = {\ frac {1} {\ pi}} \ int _ {0}^{\ frac {\ pi} {2}} \ exp \ left (-{\ frac {x ^{2}} {2 \ sin ^{2} \ theta}}-{\ frac {y ^{2}} {2 \ cos ^{2} \ theta}} \ right) d \ theta, \ quad x , y \ geqslant 0.}$

Hranice a aproximace

• Funkce Q není elementární funkcí . Nicméně hranice Borjesson-Sundberg, kde je funkce hustoty standardního normálního rozdělení,${\ displaystyle \ phi (x)}$

${\ Displaystyle \ left ({\ frac {x} {1+x^{2}}} \ right) \ phi (x) <Q (x) <{\ frac {\ phi (x)} {x}} , \ qquad x> 0,}$

stávají se pro velké x stále těsnější a často jsou užitečné.

Pomocí substituce v = u ² /2 je horní hranice odvozena následovně:

${\ Displaystyle Q (x) = \ int _ {x}^{\ infty} \ phi (u) \, du <\ int _ {x}^{\ infty} {\ frac {u} {x}} \ phi (u) \, du = \ int _ {\ frac {x^{2}} {2}}^{\ infty} {\ frac {e^{-v}} {x {\ sqrt {2 \ pi }}}} \, dv =-{\ biggl.} {\ frac {e^{-v}} {x {\ sqrt {2 \ pi}}}} {\ biggr |} _ {\ frac {x^ {2}} {2}}^{\ infty} = {\ frac {\ phi (x)} {x}}.}$

Podobně, použití a pravidla kvocient ,${\ Displaystyle \ phi '(u) =-u \ phi (u)}$

${\ Displaystyle \ left (1+{\ frac {1} {x^{2}}} \ right) Q (x) = \ int _ {x}^{\ infty} \ left (1+{\ frac { 1} {x^{2}}} \ right) \ phi (u) \, du> \ int _ {x}^{\ infty} \ left (1+{\ frac {1} {u^{2} }} \ right) \ phi (u) \, du =-{\ biggl.} {\ frac {\ phi (u)} {u}} {\ biggr |} _ {x}^{\ infty} = { \ frac {\ phi (x)} {x}}.}$

Řešení pro Q ( x ) poskytuje dolní mez.

Geometrický průměr z horní a dolní mezní dává vhodný pro přiblížení :${\ displaystyle Q (x)}$

${\ Displaystyle Q (x) \ zhruba {\ frac {\ phi (x)} {\ sqrt {1+x^{2}}}}, \ qquad x \ geq 0.}$

• Užší hranice a aproximace lze také získat optimalizací následujícího výrazu${\ displaystyle Q (x)}$

${\ displaystyle {\ tilde {Q}} (x) = {\ frac {\ phi (x)} {(1-a) x+a {\ sqrt {x^{2}+b}}}}.}$

Pro , nejlepší horní hranice je dána a maximální absolutní relativní chybou 0,44%. Stejně tak je nejlepší aproximací je dána a maximální absolutní relativní chybou 0,27%. A konečně, nejlepší dolní mez je dána a maximální absolutní relativní chybou 1,17%.${\ Displaystyle x \ geq 0}$${\ displaystyle a = 0,344}$${\ displaystyle b = 5,334}$${\ displaystyle a = 0,339}$${\ displaystyle b = 5,510}$${\ Displaystyle a = 1/\ pi}$${\ Displaystyle b = 2 \ pi}$

• Černoffova mez o Q -function je

${\ Displaystyle Q (x) \ leq e^{-{\ frac {x^{2}} {2}}}, \ qquad x> 0}$

• Vylepšené exponenciální hranice a čistá exponenciální aproximace jsou

${\ Displaystyle Q (x) \ leq {\ tfrac {1} {4}} e^{-x^{2}}+{\ tfrac {1} {4}} e^{-{\ frac {x^ {2}} {2}}} \ leq {\ tfrac {1} {2}} e^{-{\ frac {x^{2}} {2}}}, \ qquad x> 0}$

${\ Displaystyle Q (x) \ zhruba {\ frac {1} {12}} e^{-{\ frac {x^{2}} {2}}}+{\ frac {1} {4}} e ^{-{\ frac {2} {3}} x^{2}}, \ qquad x> 0}$

• Výše uvedené zobecnili Tanash & Riihonen (2020), kteří ukázali, že je lze přesně aproximovat nebo ohraničit${\ displaystyle Q (x)}$

${\ Displaystyle {\ tilde {Q}} (x) = \ sum _ {n = 1}^{N} a_ {n} e^{-b_ {n} x^{2}}.}$

Zejména se představil systematické metody pro řešení číselné koeficienty , které slibují minimax přiblížení nebo vázané: , nebo pro . S příkladem KOEF fi cients tabulkových v novinách pro relativní a absolutní chyba aproximace je menší než a , v uvedeném pořadí. Koeficienty pro mnoho variací exponenciálních aproximací a mezí byly uvolněny k otevřenému přístupu jako komplexní datová sada.${\ displaystyle \ {(a_ {n}, b_ {n}) \} _ {n = 1}^{N}}$${\ displaystyle Q (x) \ zhruba {\ tilde {Q}} (x)}$${\ displaystyle Q (x) \ leq {\ tilde {Q}} (x)}$${\ displaystyle Q (x) \ geq {\ tilde {Q}} (x)}$${\ Displaystyle x \ geq 0}$${\ displaystyle N = 20}$${\ Displaystyle 2.831 \ cdot 10^{-6}}$${\ Displaystyle 1.416 \ cdot 10^{-6}}$${\ displaystyle \ {(a_ {n}, b_ {n}) \} _ {n = 1}^{N}}$${\ displaystyle N = 25}$

• Další aproximaci for uvádí Karagiannidis & Lioumpas (2007), kteří pro vhodnou volbu parametrů ukázali, že${\ displaystyle Q (x)}$${\ Displaystyle x \ v [0, \ infty)}$${\ displaystyle \ {A, B \}}$

${\ Displaystyle f (x; A, B) = {\ frac {\ left (1-e^{-Ax} \ right) e^{-x^{2}}} {B {\ sqrt {\ pi} } x}} \ cca \ jméno operátora {erfc} \ vlevo (x \ vpravo).}$

Absolutní chyba mezi a nad rozsahem je minimalizována vyhodnocením${\ Displaystyle f (x; A, B)}$${\ displaystyle \ operatorname {erfc} (x)}$${\ displaystyle [0, R]}$

${\ displaystyle \ {A, B \} = {\ underset {\ {A, B \}} {\ arg \ min}} {\ frac {1} {R}} \ int _ {0}^{R} | f (x; A, B)-\ operatorname {erfc} (x) | dx.}$

Použitím a numerickou integrací zjistili, že došlo k minimální chybě, která poskytla dobrou aproximaci pro${\ displaystyle R = 20}$${\ displaystyle \ {A, B \} = \ {1.98,1.135 \},}$${\ Displaystyle \ forall x \ geq 0.}$

Substituce těchto hodnot a použití vztahu mezi a shora dává${\ displaystyle Q (x)}$${\ displaystyle \ operatorname {erfc} (x)}$

${\ Displaystyle Q (x) \ cca {\ frac {\ left (1-e^{-1,98x} \ right) e^{-{\ frac {x^{2}} {2}}}} {1,135 {\ sqrt {2 \ pi}} x}}, x \ geq 0.}$

Pro výše uvedenou „aproximaci Karagiannidis – Lioumpas“ jsou k dispozici také alternativní koeficienty pro přizpůsobení přesnosti pro konkrétní aplikaci nebo její transformaci na těsnou hranici.

• Striktnější a více povolný přibližování pro pozitivní argumentů je dána López-Benítez & Casadevall (2011) na základě druhého řádu exponenciální funkce:${\ displaystyle Q (x)}$${\ Displaystyle x \ v [0, \ infty)}$

${\ Displaystyle Q (x) \ zhruba e^{-sekera^{2} -bx-c}, \ qquad x \ geq 0.}$

Tvarovka koeficienty mohou být optimalizovány v kterémkoli požadovaném rozsahu argumentů, aby se minimalizovala součet čtvercových chyb ( , , k ) nebo minimalizovat maximální absolutní chyba ( , , k ). Tato aproximace nabízí určité výhody, jako je dobrý kompromis mezi přesností a analytickou sledovatelností (například rozšíření na libovolnou mocninu je triviální a nemění algebraickou formu aproximace).${\ displaystyle (a, b, c)}$${\ displaystyle a = 0,3842}$${\ displaystyle b = 0,7640}$${\ displaystyle c = 0,6964}$${\ displaystyle x \ in [0,20]}$${\ displaystyle a = 0,4920}$${\ displaystyle b = 0,2887}$${\ displaystyle c = 1,1893}$${\ displaystyle x \ in [0,20]}$${\ displaystyle Q (x)}$

Inverzní Q

Inverzní Q -funkce může souviset s inverzními chybovými funkcemi :

${\ Displaystyle Q ^{-1} (y) = {\ sqrt {2}} \ \ mathrm {erf} ^{-1} (1-2y) = {\ sqrt {2}} \ \ mathrm {erfc} ^{-1} (2 roky)}$

Funkce nachází uplatnění v digitální komunikaci. Obvykle se vyjadřuje v dB a obecně se nazývá Q-faktor : ${\ displaystyle Q^{-1} (y)}$

${\ Displaystyle \ mathrm {Q {\ text {-}} faktor} = 20 \ log _ {10} \! \ left (Q^{-1} (y) \ right) \! ~ \ mathrm {dB}}$

kde y je bitová chybovost (BER) digitálně modulovaného analyzovaného signálu. Například pro QPSK v aditivním bílém Gaussově šumu se výše definovaný Q-faktor shoduje s hodnotou v dB poměru signálu k šumu, která poskytuje bitovou chybovost rovnou y .

Hodnoty

Funkce Q je dobře přehledná a lze ji vypočítat přímo ve většině matematických softwarových balíčků, jako jsou R a ty, které jsou k dispozici v Pythonu , MATLABu a Mathematice . Některé hodnoty Q -funkce jsou uvedeny níže pro referenci.

Zobecnění na vysoké rozměry

Funkci Q lze zobecnit na vyšší dimenze:

${\ Displaystyle Q (\ mathbf {x}) = \ mathbb {P} (\ mathbf {X} \ geq \ mathbf {x}),}$

kde následuje vícerozměrné normální rozdělení s kovariancí a prahová hodnota je pro nějaký pozitivní vektor a kladnou konstantu . Stejně jako v jednorozměrném případě neexistuje pro Q -funkci jednoduchý analytický vzorec . Nicméně Q -function lze aproximovat libovolně, stejně jako se stává větší a větší. ${\ displaystyle \ mathbf {X} \ sim {\ mathcal {N}} (\ mathbf {0}, \, \ Sigma)}$${\ displaystyle \ Sigma}$${\ Displaystyle \ mathbf {x} = \ gamma \ Sigma \ mathbf {l} ^{*}}$${\ displaystyle \ mathbf {l} ^{*}> \ mathbf {0}}$${\ displaystyle \ gamma> 0}$${\ displaystyle \ gamma}$

Reference